海上风电集群与火电打捆外送系统短路比定义及影响因素分析

陈作舟，余浩，王盼盼，陈鸿琳，陈武晖*

（1.江苏大学电气信息工程学院，江苏省 镇江市 212013；2.广东电网有限责任公司电网规划研究中心，广东省 广州市 510080；3.太原理工大学电气与动力工程学院，山西省 太原市 030024）

0 引言

海上风电出力水平普遍优于陆上风电，同等条件下海上风力机的年发电量比陆上高70%。但海上风电同其他清洁能源发电一样，具有波动性、间歇性和不可预测性，增加了电网调峰、调频的压力。海上风电同陆上火电打捆并网外送，是改善上述问题的有效措施[1]。

受到随新能源并网接入交流电网的电力电子设备数量增加以及电网容量扩大的影响，交流系统电网强度降低，设备间耦合程度因而加剧，甚至会引发次同步振荡相关问题[2-8]。因此，新能源馈入电网后系统强度能较好地反映新能源电力电子设备接入交流电网的次同步振荡风险[9-10]，这对于保证电网稳定运行起到重要作用。

为解决这一问题，工程中常采用短路比(shortcircuit ratio，SCR)的定义来反映电力电子设备馈入交流系统的相对强度，其计算方式由交流系统的短路容量和电力电子设备额定容量计算得出[11-13]。在常规的单馈入系统中，常以短路比2和3作为区分“较弱”“弱”“强”系统的边界短路比[14]。单馈入系统短路比能较清晰地反映交流网络相对强度并具有明确的物理概念[15]，与其相比，由于新能源多场站并网中常存在耦合、各场站间各自作用，以及多回交直流间相互影响难以考虑等问题，使得新能源多馈入系统的定义及指标更难分析[16-17]。近年来，有多位学者提出多馈入交直流系统短路比定义。文献[18-19]考虑交直流混联系统的运行方式，提出了多种多馈入相互作用的短路比定义，其中比较有名的是国际大电网组织

(international council on large electric systems，CIGRE)提出的多馈入短路比(multi-infeed shortcircuit ratio，MISCR)、基于传统直流的加权短路比(weighted short circuit ratio，WSCR)以及复合短路比(composite short circuit ratio，CSCR)定义。在此基础上，文献[20]从小干扰稳定性特征方程特征根的角度提出了一种可度量多馈入交直流系统强度的广义短路比定义，弥补了传统多馈入短路比的理论缺陷及适用范围，反映了其小干扰稳定裕度。在定义的广义短路比基础上，文献[21-22]对基于特征根角度出发的短路比定义开展研究，分析了影响多馈入交直流系统广义短路比变化的因素，以提高多馈入系统的合理规划和安全稳定运行。不同于多直流馈入系统的短路比计算，文献[23]给出计及多能源场站间相互影响的新能源多场站短路比定义，提出更详细完备的短路比计算公式，适用于广义场景下电压强度评估。

目前的短路比定义主要针对新能源单/多馈入系统，同时上述研究也没有从根本上解决多馈入短路比物理意义不明确的问题[24]，且还没有统一标准的多馈入短路比定义。对于目前较常采用的风火打捆并网运行方式，其短路比暂无明确定义和详细的计算公式，且对风火打捆场景下短路比的影响因素及变化规律还未有相应的研究分析，常规广义短路比定义对海上大型风电场风火打捆系统次同步振荡分析的适用性也有待分析。因此，从理论和工程上完善风火打捆短路比定义，对电网的发展规划和安全稳定运行具有重要意义。

针对以上问题，本文提出了一种双海上风电集群与陆上火电打捆外送系统短路比定义，给出了其计算方法，该方法以解耦的形式计及双风电集群相互作用对次同步振荡的影响。从数学上分析了风火打捆模型中影响短路比的各因素对次同步振荡稳定性的影响，最后通过仿真算例进行了验证。

1 风电打捆系统下的风电短路比定义

1.1 单馈入风电场的短路比定义

通常在计算单馈入系统时对交流系统进行戴维南等值简化，将系统简化为一个理想电压源串联等值阻抗[25]。一个典型单风场交流并网系统如图1 所示，风电并网点A 处短路比KSCRA定义为A处交流系统短路容量和风电场额定功率的比值，其计算公式为

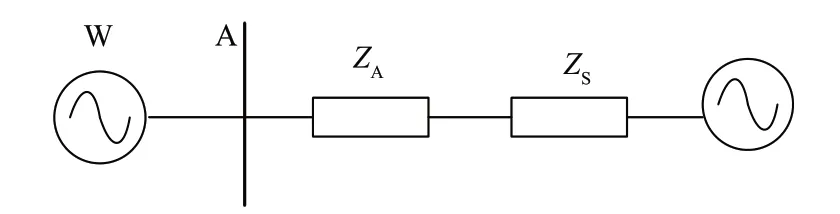
图1 单个风电场交流并网系统Fig.1 Alternating current grid-connected system for a single wind farm

式中：SA=/Zeq，为风电场并网点A处的交流系统短路容量，其中UA为系统在A 点处的额定电压，Zeq=ZA+ZS，ZA为线路中变压器阻抗和线路阻抗的总和，ZS为交流系统的等效阻抗；风电场W的容量SW=nSG，其中n为风机台数，SG为单台风机的额定容量。

由式(1)可知，在采用相同型号风机的情况下，影响交流系统短路比的因素为风机台数，风机台数的增多会使交流系统短路比明显降低。

1.2 双风场解耦系统短路比定义推广

短路比常用于反映单风场交流并网系统的电网强度，但大型海上风电输送常常由多个风电场构成，因此需要开展短路比在多风电场系统的计算推广分析。本文主要讨论双风场下等值解耦模型所应用的场景。

以海上大型风电场为例，2 个风电场并网的送出系统可以用图2所示的系统表示。2个风电场并网点1、2 及汇集线3 处的短路比KSCR1、KSCR2、KSCR3分别表示为：

图2 双风场交流并网系统Fig.2 AC grid-connected system for dual wind farms

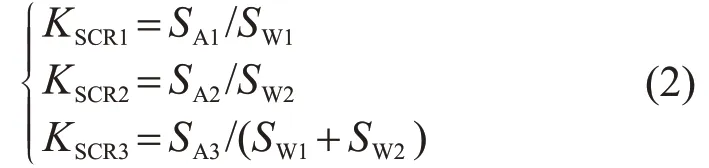
该双风场交流并网系统可以解耦为图3 所示的2个等价单风场并网系统[26]，解耦后2个单风场系统A和B的短路比分别为：

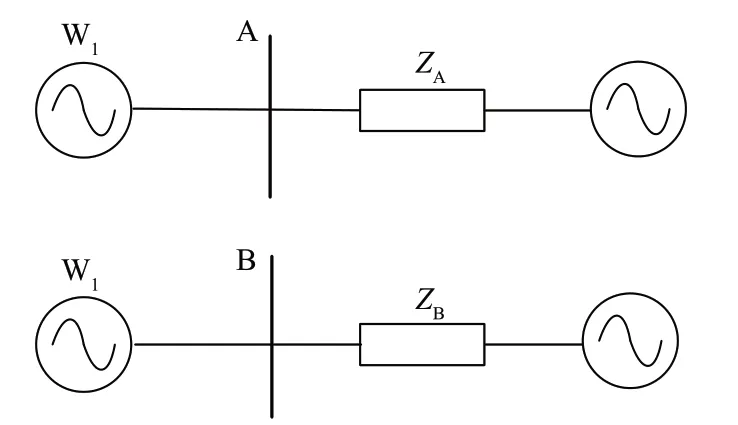
图3 双风场解耦系统Fig.3 Dual wind field decoupling system

式中

根据短路比定义，短路比越大，系统的电网强度越高。由式(5)可知KSCRA恒小于KSCRB，即系统稳态运行时，解耦后图3 中单风场系统A 点的电气强度一定弱于B 点，因此可以选择A 点短路比KSCRA作为双风场解耦系统的参考短路比，以判断整体系统的强弱。风电场不发生次同步振荡的最小短路比定义为系统临界短路比，当作为解耦系统参考短路比的KSCRA达到临界值时，双风场系统发生次同步振荡。

1.3 考虑风火打捆并网的双风场解耦系统的短路比定义

目前将风电、火电二者通过打捆并网外送是我国实现新能源基地电力外送的重要途径。风火打捆系统中的风电场含有大量电力电子设备。因此在计算短路比时，从风火打捆系统整体出发，忽略风火打捆系统场站内部相互影响，将与受端电源极为相似的火电机组阻抗并入受端系统。图4为火电接入双风场交流并网系统示意图。

图4 中，T1为火电机组，Z4为火电机组阻抗、火电并网点至汇集线的变压器阻抗、线路阻抗三者折算后的等值阻抗。此双风场风火打捆系统的参考短路比KSCRA为

图4 火电接入双风场交流并网系统示意图Fig.4 Schematic diagram of AC grid-connected system for thermal power access to dual wind farms

由于Z4并入受端系统，因此Zsys=Z3//Z4=Z3×Z4/(Z3+Z4)，SA1=/(Z1+Zsys)，SA2=/(Z2+Zsys)，SA3=/Zsys。

从式(6)可以看出，在风火并网系统中各线路参数不调整的情况下，影响该双风场解耦系统短路比的变量有3个，其中2个为风电场容量的相关变量(风机数n1和n2)，1个为受端相关变量(系统阻抗Z3)。

2 短路比影响因素分析

以图5 所示的某实际双风场风火打捆交流输送电网为例，采用PSCAD/EMTDC仿真平台搭建此系统时域仿真模型，对不同风场短路比下系统等值阻抗、风场容量比例、风火打捆比例对风火系统次同步振荡稳定性的影响进行分析。

图5 双风场风火打捆交流系统拓扑图Fig.5 Topological diagram of wind and fire bundling AC system in double wind farms

1）风火打捆并网对短路比的影响

在双风场风火打捆系统中保持各风场容量及风火比例不变，仅改变系统阻抗Z3的大小，下面分2种情况讨论Z3与KSCRA的关系。

①当未接入火电时，各参数设为标幺值，取Zsys=Z3，假定SG=1.0 pu，Un=1.0 pu，n1=n2=1.0 pu，Z1=Z2=2.0 pu，Z3在1.0～1.5 pu 变化，系统阻抗Z3与短路比KSCRA的变化关系如图6中蓝色实线所示。

②当接入火电后，取Zsys=Z3//Z4=Z3×Z4/(Z3+Z4)，假定SG=1.0 pu，Un=1.0 pu，n1=n2=1.0 pu，Z1=Z2=2.0 pu，Z3=0.1,0.2,0.3,…,1.5 pu。若风火比例不变，在风电容量一定的情况下火电容量也确定，火电机组等值电抗相关的参数Z4=1.0 pu。火电接入后原系统阻抗Z3与短路比KSCRA的关系如图6 中红色虚线所示。

图6 火电接入对短路比影响关系图Fig.6 Relationship between thermal power access and short-circuit ratio

根据图6 中关系，无论火电是否接入，随着原系统阻抗Z3的增加，双风场交流系统短路比KSCRA都随之下降。可以看出，风火打捆系统短路比KSCRA相比于火电不接入时的短路比明显提高，并且火电接入后短路比的下降速度呈现先快后慢的变化趋势。

从图6 中火电接入的曲线可以看出，采用风火打捆的外送模式，当影响短路比的绝大多数参数都固定时，短路比会趋近于一个边界值，即对于某一项影响因素，短路比存在一个上、下限的取值范围。同时对于与火电打捆输送的风电，其短路比变化范围随原系统阻抗变化较小。

由上述分析可以得出，采用风火打捆的形式可以有效提高系统强度。对比纯风电输送系统，风火打捆主要是通过降低系统侧阻抗的形式来提高系统短路比，同时风火打捆并网对系统短路比的降低起到减缓趋势的作用。

2）风场容量比例对短路比的影响

式(6)中的变量含有风机台数n1和n2，因此考虑固定风火比例及系统阻抗Z3来研究双风场容量比例与参考短路比KSCRA的关系，假定SG=1.0 pu，Un=1.0 pu，Z1=Z2=2.0 pu，Z4=1.0 pu，Z3=0.6 pu。风机总台数为2.0 pu 时不同风场容量比例得到的短路比结果如表1所示。

表1 风机总台数为2.0 pu时不同风场容量比例对应的双风场系统短路比Tab.1 Short-circuit ratio of dual wind farm system corresponding to different wind farm capacity ratios when the total number of wind turbines is 2.0 pu

通过分析上述计算结果可知，在其他条件固定的情况下，改变2 个风场容量比例T=n1∶n2，会对双风场系统短路比造成影响。在两风场各线路等值阻抗近似相等的情况下，T=1∶1时为短路比最大的情况。考虑风场容量不应超出输电线路和变压器极限，以及风机的切入、切出应保持一个合理的范围，从表1来看，T变化对短路比的影响较小，改变双风场容量比例对系统稳定性造成的影响有限。

3）风火打捆比例对短路比的影响

在风火打捆系统中，火电机组等值为阻抗后，电压源需考虑同步电机自身的阻抗，火电容量和风电容量一样成为影响短路比的变量，因此有必要对在风火打捆中风火配置比对系统安全稳定运行的影响进行研究。但如果是采用风电总容量不变、火电容量改变的研究策略，其研究过程类似于改变系统等值阻抗大小，因此考虑固定系统阻抗Z3、火电相关阻抗Z4、双风场容量比例T不变，来研究改变风火打捆比例对短路比KSCRA的影响。假定SG=1.0 pu，Un=1.0 pu，Z1=Z2=2.0 pu，Z3=0.6 pu，Z4=1.0 pu。假设双风场容量比例T固定为1∶1，改变风火打捆容量比例也就是改变风电容量，即改变单风场参与发电的风机台数。单风场风机台数n为0.2～1.2 pu，得到n与KSCRA关系如图7所示。

图7 双风场系统短路比KSCRA与风机台数关系Fig.7 Relationship between short-circuit ratio KSCRA and the number of wind turbines in the double wind farm system

由图7 可见，随着风场中风机台数的增加，双风场系统中短路比下降。由此分析得出结论：在风火打捆系统中风电容量增加、风电占比提高的情况下，系统短路比降低，电气强度变弱。从图7 还可以看出，当风火比例变化时，除了呈现和系统等值阻抗一样的“先快后慢”趋势外，短路比变化的范围还很大。取n=1.0 pu 和n=0.3 pu，绘制原系统等值阻抗与短路比的关系图，如图8所示。

图8 风火打捆系统风电总容量与风场短路比关系图Fig.8 Relationship between total wind power capacity of wind-fire bundling system and short-circuit ratio of wind farm

同时取风机总台数为0.6 pu，计算得到n1∶n2=1∶1、2∶3、1∶2时的短路比，结果如表2所示。

表2 风机总台数为0.6 pu时不同风场容量比例对应的双风场系统短路比Tab.2 Short-circuit ratio of dual-wind farm system corresponding to different wind farm capacity ratios when the total number of wind turbines is 0.6 pu

从图8和表2可以看出，风火打捆系统中风电总容量对短路比的影响远高于系统等值阻抗和风场间容量比例对短路比的影响。n=0.3 pu 时风场短路比变化范围是n=1.0 pu 时的2～3 倍，同时n=0.3 pu时风场短路比远大于n=1.0 pu时。风电总容量是影响风场短路比最大的因素，风电容量过大时，短路比可变化范围很小，此时系统电气强度不仅整体低而且十分脆弱，若短路比略微变化，就可能低于系统临界短路比。而打捆系统中风电占比较低时，短路比整体处于一个较高的水平，电网强度也较高，给短路比变化留有较宽裕的安全空间，在这种情况下，系统等值阻抗出现一些变化或者双风场在保证总出力下出现风机需要切入、切出的情况，系统依然可以保持较高的电网强度。风电总容量较低时，短路比即使处于最低值，仍然可以高于临界短路比。

根据上述影响因素的分析，在双风场风火打捆系统中，系统等值阻抗的增加、风场容量比例的增大、风火打捆比例的下降，都会导致系统参考短路比降低，从而使电网强度变弱，其中风火打捆比例是占最大比重的影响因素。另外，结合表1、2 和图8 可知，系统等值阻抗对短路比的影响范围会大于不同风场容量比例的影响范围。

3 仿真验证

3.1 仿真方案

以图5 中PSCAD/EMTDC 仿真平台上双风场风火打捆交流输送系统为例进行仿真验证。系统仿真时，设计以下3种方案。

1）CASE-A。保持发电的风机台数总量nA=nA1+nA2=688 不变，风机比例TA=1∶1不变，调整系统阻抗Z3，使得式(6)中风场短路比KSCRA分别为2.4、2.3、2.2、2.1，根据对应反函数计算得到系统等值阻抗Z3分别为1.70、4.26、9.02、20.92 Ω。

2）CASE-B。保持发电的风机台数总量nB=nB1+nB2=600 不变，系统等值阻抗Z3=21 Ω 不变，改变风场风机比例TB分别为1:1、2:3、1:2时，相对应的风场短路比如表3所示。

表3 CASE-B相对应的双风场系统短路比Tab.3 Short-circuit ratio of double wind farm system corresponding to CASE-B

3）CASE-C。保持发电的双风场风机台数比例TC=1∶1 不变，系统等值阻抗Z3=21 Ω 不变，改变双风场风机台数总量nC=nC1+nC2的数量分别为500、800、1 000 时，相对应的风场短路比如表4所示。

表4 CASE-C相对应的双风场系统短路比Tab.4 Short-circuit ratio of double wind farm system corresponding to CASE-C

3.2 仿真结果分析

1）CASE-A仿真结果分析

CASE-A 的仿真设置时，通过调整Z3参数，使风场短路比在0～2 s内为2.4，2～3 s内为2.3，3～4 s 内为2.2，4～6 s 内为2.1；6～10 s 过程中，随着Z3参数的增大，短路比逐渐降低。仿真结果如图9、10 所示，可以看出，在6 s 内，风场短路比从2.4降至2.1，火电电磁扭矩的波动曲线比较稳定；6 s后系统等值阻抗逐渐增加，火电机组电磁扭矩波形开始出现振荡发散现象；9 s后系统等值阻抗Z3继续增大，系统短路比继续下降，此时系统振荡发散呈现进一步扩大趋势。图11为对火电电磁扭矩进行FFT 分析的频谱图，振荡主要由频率为35 Hz和70 Hz的振荡分量构成，其谐波含量分别为4.05%和4.10%。

图9 CASE-A短路比变化示意图Fig.9 Schematic diagram of short-circuit ratio change of CASE-A

图10 CASE-A火电机组电磁扭矩仿真波形图Fig.10 Simulation waveform of electromagnetic torque of CASE-A thermal power unit

图11 6～10 s火电机组电磁扭矩频谱分析Fig.11 Spectrum analysis of electromagnetic torque of thermal power unit within 6-10 s

风电有功功率仿真结果如图12所示，可以看出，与火电电磁扭矩振荡情况类似，图12(b)显示风电有功功率与火电电磁扭矩同时开始出现波动，图12(c)中从6 s 开始出现明显振荡现象，并在8 s后伴随有功功率的急剧下降。图13为对风电有功功率进行FFT 分析的频谱图，风电有功功率振荡主要由频率为35 Hz和70 Hz的振荡分量构成，其谐波含量分别为3.50%和3.55%。这2个振荡分量和图11中火电电磁扭矩振荡的2个主要分量相等。

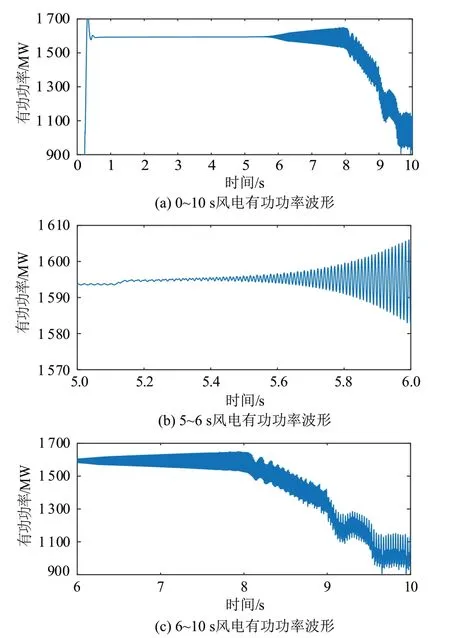
图12 CASE-A风电有功功率仿真波形图Fig.12 CASE-A wind power active power simulation waveform diagram

图13 6～10 s风电有功功率频谱分析Fig.13 Wind power active power spectrum analysis within 6-10 s

从以上分析可以看出，短路比低于2.1后，电磁扭矩和风电功率波动逐渐增大，对于此参数组，2.1为其临界短路比。风电有功功率和火电电磁扭矩仿真结果表明，随着系统等值阻抗增加，风场短路比下降，导致发生次同步振荡现象，并随着短路比继续下降，振荡发散进一步扩大。

2）CASE-B仿真结果分析

CASE-B 的仿真结果如图14、15 所示，其中3条曲线分别为风场A、B风机台数比为1∶1、2∶3、1∶2的情况。可以看出，在不超出风机容量限制的情况下，双风场间风机3 种不同容量比例对应的风电有功功率波动都很小，并且火电电磁扭矩的振荡范围相差不大。对风电有功功率和火电电磁扭矩进行FFT 分析，所得频谱图分别如图16、17所示。可见，风电有功功率振荡主要由50 Hz 和104 Hz的振荡分量构成，其谐波含量分别为1.0%和7.0%；火电电磁扭矩振荡主要由50 Hz和98 Hz的振荡分量构成，其谐波含量分别为1.5%和4.0%。风电有功功率和火电电磁扭矩仿真结果表明，在系统阻抗和风火比例确定的情况下，双风场风机容量比例变化对风电有功功率波动影响较小，风机台数比增加至1∶2 的情况下也未发生次同步振荡现象，火电电磁转矩振荡仍维持在一个很小的范围。

图14 CASE-B风电输电有功功率曲线Fig.14 Active power curve of CASE-B wind power transmission

图16 双风场台数比为2∶3时风电有功功率频谱分析Fig.16 Wind power active power spectrum analysis when the ratio of double wind farms is 2∶3

图15 CASE-B火电机组电磁扭矩曲线Fig.15 Electromagnetic torque curve of CASE-B thermal power unit

图17 CASE-B火电机组电磁扭矩频谱分析Fig.17 Analysis of electromagnetic torque spectrum of CASE-B thermal power unit

3）CASE-C仿真结果分析

CASE-C 的仿真结果如图18、19 所示。从图18 可以看出，当风机为500 台时，功率曲线波动很小；当风机增加至800 台时，功率波动范围约为5%额定功率，计算后约90 MW；当风机增加至1 000 台时，输出功率振荡范围非常大，超过30%额定功率。CASE-C 中对1 000 台投入风机下火电电磁扭矩和风电的有功功率振荡进行FFT分析，所得频谱图分别如图20、21 所示。可以看出，火电电磁扭矩振荡主要由38 Hz和78 Hz的振荡分量构成，其谐波含量分别为22.0%和5.0%；风电有功功率振荡主要由39 Hz 和78 Hz 的振荡分量构成，其谐波分量分别为15.8%和6.4%。

图18 CASE-C风场输出功率曲线Fig.18 CASE-C wind farm output power curve

图20 1 000台风机投入发生次同步振荡时火电电磁扭矩频谱分析Fig.20 Spectrum analysis of thermal power electromagnetic torque when 1 000 wind turbines are put into operation

图21 1 000台风机投入发生次同步振荡时风电有功功率频谱分析Fig.21 Wind power active power spectrum analysis when 1 000 wind turbines are put into operation

综合分析图18—21 可知，相比于CASE-B，CASE-C 中随着参与发电的风机台数不断增加，风火比例中风电占比增加，风场短路比下降，导致电网强度减弱十分明显，最终产生的次同步振荡波形幅度更大。因此，风火比例是短路比影响因素中占比最大的部分。

同时根据表4 和图19 波形可知，当风机总数为800 台时未发生次同步振荡现象，当风机总数增加至1 000 台时，出现了严重的次同步振荡现象，该参数组的临界短路比应为1.4～1.8，小于CASE-A中的临界短路比2.1。

图19 CASE-C火电机组电磁扭矩振荡曲线Fig.19 CASE-C thermal power unit electromagnetic torque oscillation curve

综合以上3 个方案可以推测，短路比公式中各因素对临界短路比影响比重不同。目前，解耦计算的结果无法给出一个适用于多数工况的临界短路比范围，只能对电力电子设备和线路参数都不变化的具体情境给出参考临界短路比，下一步可以对其加入权重系数进行优化。

4 结论

提出了风火打捆系统短路比计算方法，从风火打捆系统整体出发，以解耦的方式对双风场系统进行处理，简便且不失准确性，并将与受端电源极为相似的火电机组阻抗并入受端系统，得到系统参考短路比计算公式。针对双风电集群与火电打捆外送模式结论具有通用性，研究该模式中影响短路比的因素，并进行理论分析和仿真验证，得到以下结论：

1）通过数学模型计算，从短路比的角度分析风火打捆系统和纯风电外送系统区别，提出风火打捆中火电可以作为阻抗后电源。相比于纯风电输送，风火打捆并网提高了整体系统的短路比，并且在系统阻抗增大的情况下减缓短路比的下降速度，风电经火电打捆可增强风电输送的稳定性。

2）通过数学模型和仿真验证可知，双风场风火打捆系统短路比影响因素中，风火打捆比例对短路比影响最大，保持风电总输送量一定的情况下，风场间风机合理范围内切入、切出对风场短路比影响较小。

3）线路参数和电力电子元器件数目保持不变，3 个影响因素对该双风场风火打捆系统的临界短路比影响比重不同，风机配比影响最小，风火比例的影响比重最大，因此解耦计算获得的短路比公式需要进行优化，可对各影响因素加入权重系数进行分析，以得出可适用多数工况的临界短路比范围。