山地光伏阵列布置方法和排间距计算
罗耿
(中国电力工程顾问集团新能源有限公司,北京市 西城区 100120)
0 引言
在中国鼓励光伏发展的政策引导下,光伏行业快速发展[1-5]。截至2020年年底,中国光伏发电装机容量累计达到25 343万kW[6]。光伏电站项目开发场址也越来越多地从平坦地面转移到山地[7]。为了达到经济效益最大化,对山地光伏电站的优化设计必不可少,其中对任意坡面下光伏阵列的布置方法和排间距的计算尤其重要[8],因为其直接影响了光伏系统发电量和项目成本。
文献[9]通过影子倍率法计算了平坦地面的光伏阵列间距。文献[10]推导了正北坡场地下光伏阵列的间距公式。文献[11-12]对南北坡不同坡度下光伏阵列间距进行了计算和分析。文献[13]对方位角为正南、正西、正北、正东的斜坡下阵列间距进行了研究。文献[14-15]对任意坡面朝向和坡度下的阵列间距公式进行了推导,但使用坡面的分解方法模型较复杂。文献[16-17]使用PVsyst软件对山地光伏系统的排布进行了研究。文献[18]研究了阵列间距对发电量的影响,提供了一种从经济性角度确定合适阵列间距的方法。文献[19]研究了光伏组件倾角、间距综合影响下最佳倾角和阵列间距的确定方法。
以上文献研究了平坦地面或特定坡面的光伏阵列间距,一般默认组件为某一种布置方法,鲜少对多种布置方法进行比较分析。基于此,本文通过数学模型,推导了在任意地形条件下随坡倾角布置和正南倾角布置时光伏阵列排间距的计算方法,并对比分析了2 种布置方法下排间距的变化规律。本文侧重理论计算和分析,以期为设计人员对光伏电站进行经济性分析和系统优化提供理论参考。
1 光伏阵列布置方法
光伏阵列排布设计中最重要的便是光伏组件的倾角[20]、方位角[21]和光伏阵列排间距,这3个参数均影响光伏系统的发电量。根据设计规范,平地光伏方阵各排、列的布置间距应保证每天09:00—15:00(当地真太阳时)时段内前、后、左、右互不遮挡[22]。通常光伏电站设计均按照该标准,所以间距对发电量的影响较小,但相比于光伏组件倾角和方位角,排间距直接影响了占地和电缆用量等,故对光伏电站成本影响较大。综上可知,对于平地光伏项目,光伏组件倾角和方位角更多地影响收益,而排间距更多地影响成本。
设计规范仅对平地光伏系统提出要求,即光伏组件安装方位角宜采用正南方向。但山地光伏项目的地形复杂,有时难以保证光伏组件方位朝向正南,有时也难以保证光伏组件每天09:00—15:00时段内不被遮挡。
为了探索山地光伏如何更优地布置,本文从排间距的计算入手进行研究,仍以平地光伏每天09:00—15:00 时段内不被遮挡为前提计算坡面上光伏阵列排间距。本文定义了如下2种布置方法:
1)随坡倾角布置。光伏组件方位角与坡面方位角一致,并与水平面呈一定的倾角。
2)正南倾角布置。光伏组件方位角为0°(朝向正南),并与水平面呈一定的倾角。
显而易见,对于同一非正南、正北斜坡,光伏组件采用正南倾角布置一定比随坡倾角布置发电量高,但2 种布置方法在排间距上表现如何未知,本文将对此展开研究。
2 2种阵列布置下的排间距建模
2.1 太阳光线数学模型
以当地水平面建立x、y轴所在平面,正南方向为x轴,正东方向为y轴,通过太阳高度角α和方位角λ确定太阳光线位置,如图1所示。
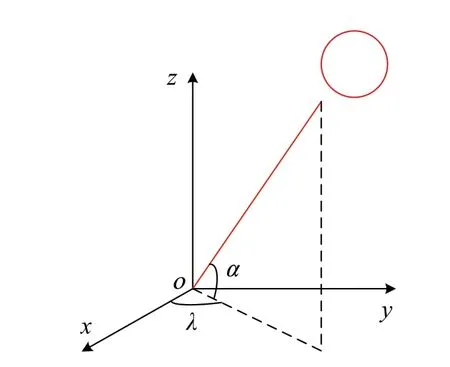
图1 太阳光线数学模型Fig.1 Mathematical model of solar rays
太阳高度角和方位角采用以下公式[23]计算:

式中:φ为地理纬度,本文纬度均指北纬;δ为太阳赤纬角;ω为时角。对于太阳方位角λ,正南为0°,正西为-90°,正东为90°。
太阳赤纬角、时角的计算公式[24]如下:
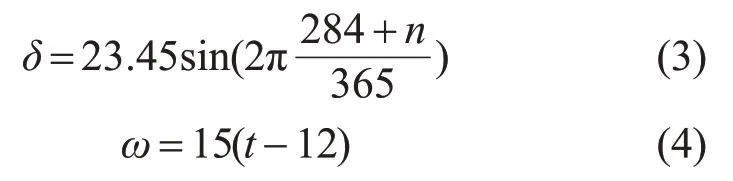
式中:n为日序,其值为0~365;t为真太阳时。
从而得到太阳光线的方向向量为
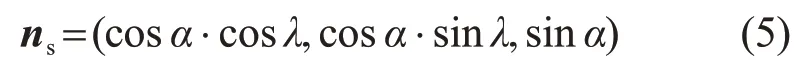
2.2 随坡倾角布置数学模型
光伏组件随坡倾角布置,则光伏组件的方位角与坡面方位角θ相等,对于坡面方位角θ,正南为0°,正西为90°,正东为-90°。光伏组件倾角β为组件所在平面与水平面之间的夹角,那么组件倾角β≥坡度γ。其中光伏组串竖向宽度DE为dwidth,光伏阵列排间距为dpitch。
在右手直角坐标系中建立光伏组件和坡面的数学模型,如图2 所示,光伏组件和坡面初始位置均朝向正南。
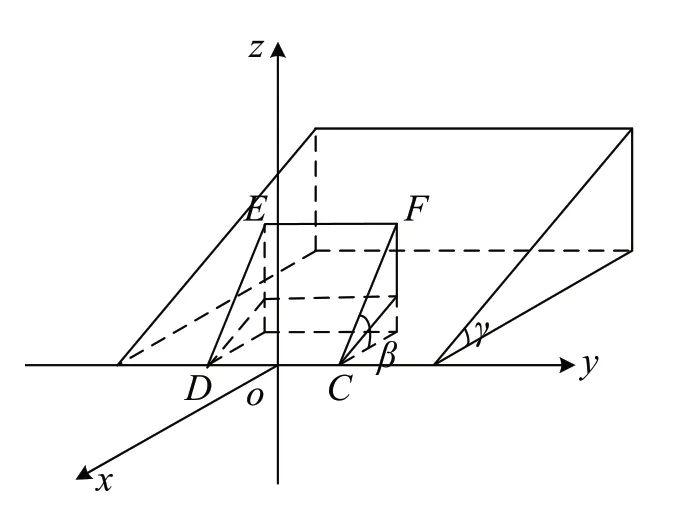
图2 光伏组件和坡面初始正南朝向示意图Fig.2 Initial south-facing orientation of photovoltaic module and slope
从初始正南位置,以z轴为旋转轴,转动斜坡,光伏组件CDEF随斜坡旋转,到达图3 所示位置。只有早晚的太阳高度角最低,影子才最长,所以求解前后排间距dpitch,即求09:00 或15:00 组件的上边缘EF落到坡面上的影子到直线CD的距离,易知组件上边缘线段EF的投影一定与直线CD平行,为简化计算,求解A的投影B到直线CD的距离即可。计算思路为:先通过联立直线AB方程和坡面方程求出B点坐标;然后通过向量积关系求出B点与直线CD的距离。

图3 随坡倾角布置下光伏组件和坡面数学模型Fig.3 Mathematical model of photovoltaic module and slope under slope’s azimuth-tilt layout
直线AB的方向向量如式(5)所示。根据图3几何关系可得到坡面法向量:

A点坐标为

直线CD的方向向量为
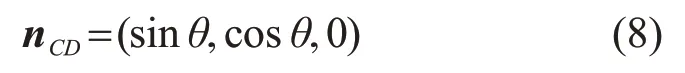
则可推导出直线AB的方程式:

坡面方程为

联立式(9)、(10),即可求出B点坐标:
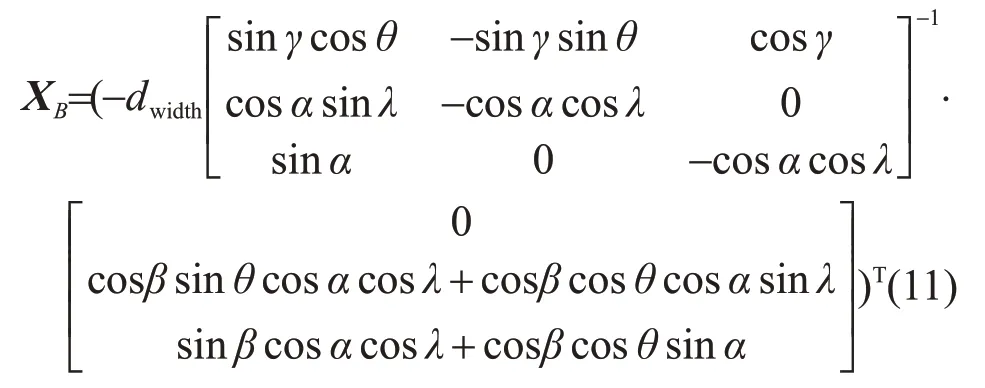
则AB的距离表示为

经分析,可能会出现以下2种特殊情况:1)光线经过组件上边缘与坡面相交于组件的前面,而非后面;2)光线先穿过坡面再经过组件上边缘。这2 种情况可能会计算出错误的结果,故增加以下判定条件:1)当当ns·<0时,dAB=0。
分别计算09:00 和15:00 时AB的距离d9和d15,两者取最大值得到排间距,即
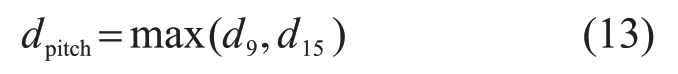
2.3 正南倾角布置数学模型
采用正南倾角布置,则光伏组件的方位角为0°,在坡面非正南朝向时,组件倾角一定大于坡度。
从图2 所示的正南初始位置,以z轴为旋转轴,转动斜坡,以过原点o的组件平面法向量为旋转轴,转动组件CDEF使组件下边缘CD与坡面贴合,到达图4(a)所示位置。求解前后排间距d′pitch,与随坡倾角布置一样,即求A的投影B到直线CD的距离。计算思路同2.2节。

图4 正南倾角布置下光伏组件和坡面数学模型Fig.4 Mathematical model of photovoltaic module and slope under south-tilt layout
直线AB的方向向量如式(5)所示。根据几何关系可得到坡面法向量,如式(6)所示。
组件平面法向量为
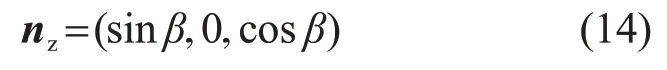
联立坡面方程和组件平面方程:
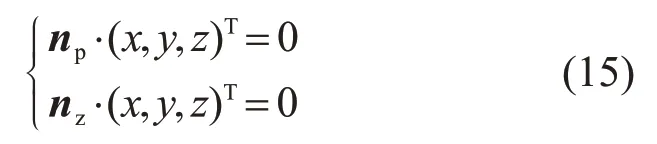
得到交线CD方程:

则直线CD的方向向量为

根据以下条件可得式(18):1)A点在组件平面内;2)直线OA与直线CD垂直;3)dOA=dwidth。
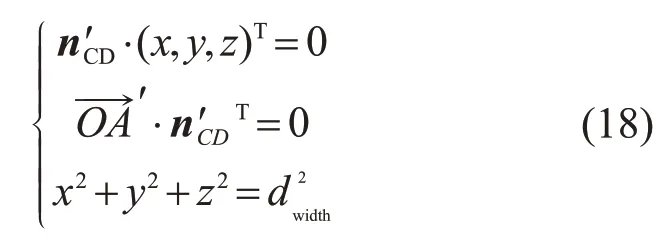
由式(18)即可求出A点坐标,得到2个关于原点对称的坐标,取zA>0 的一组,即(xA,yA,zA),从而推导出直线AB的方程式:
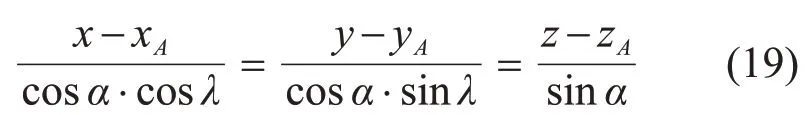
联立式(19)与坡面方程式(10),即可求出B点坐标。整理可得B点坐标为
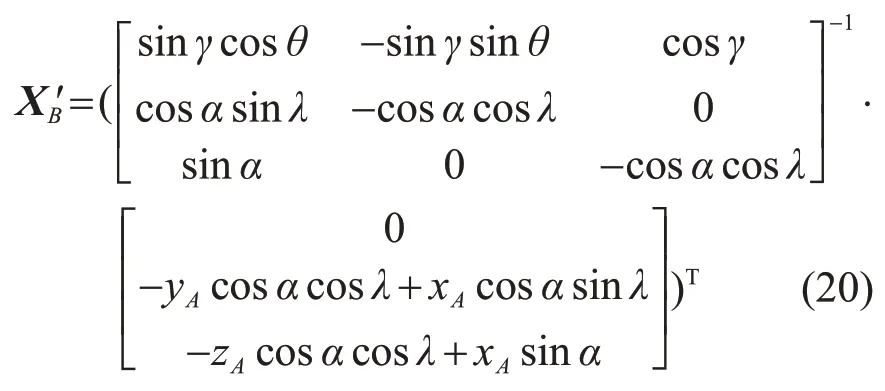
则AB的距离

经分析,该布置方法也可能会出现特殊情况,即光线先穿过坡面再经过组件上边缘,故增加以下判定条件:当ns·<0时,d′AB=0。
分别计算09:00和15:00时AB的距离d′9和d′15,两者取最大值得到排间距,即

3 排间距分析
因为上午和下午太阳位置是对称的,斜坡南偏西和南偏东也是对称的,所以排间距值只与方位角的绝对值有关,故本文排间距分析及图表中均只体现方位角为正(即南偏西坡)的情况,方位角为负的情况不再体现,特此说明。
3.1 随坡倾角布置分析
对于随坡倾角布置,显而易见,有以下结论:
1)排间距会随着坡度增加而减小;
2)排间距会随着纬度增加而增大;
3)排间距会随着组件倾角增加而增大。
使用某主流组件进行设计,光伏组串竖向宽度dwidth为4.036 m,分别在纬度20°、35°、50°,坡度10°、20°下计算排间距。为便于对照分析,组件倾角固定38°不变,得到不同纬度、坡度下排间距随方位角变化的曲线,如图5所示。

图5 不同纬度、坡度下排间距随坡面方位角的变化曲线(随坡倾角布置))Fig.5 Variation curves of row pitch with slope azimuth at different latitudes and slopes(slope’s azimuth-tilt layout)
从图5 可以看出,随着方位角增大,排间距先增大后减小,方位角在45°左右(纬度20°对应方位角41°,纬度35°对应方位角43°,纬度50°对应方位角47°)时,排间距出现拐点。
由此可见,采用随坡倾角布置方法,不论方位角增加多少,排间距始终维持在较低水平,可以节省用地和项目成本。当然,随着方位角逐渐增大,倾斜面峰值日照时数也会逐渐减小,当方位角过大时,对发电量影响较大。通过PVsyst 仿真,倾角设置为35°,得到不同方位角下北京地区倾斜面峰值日照时数,如表1所示。
由表1可以看出,当方位角低于30°时,峰值日照时数损失较小,超过30°以后峰值日照时数下降幅度较大。
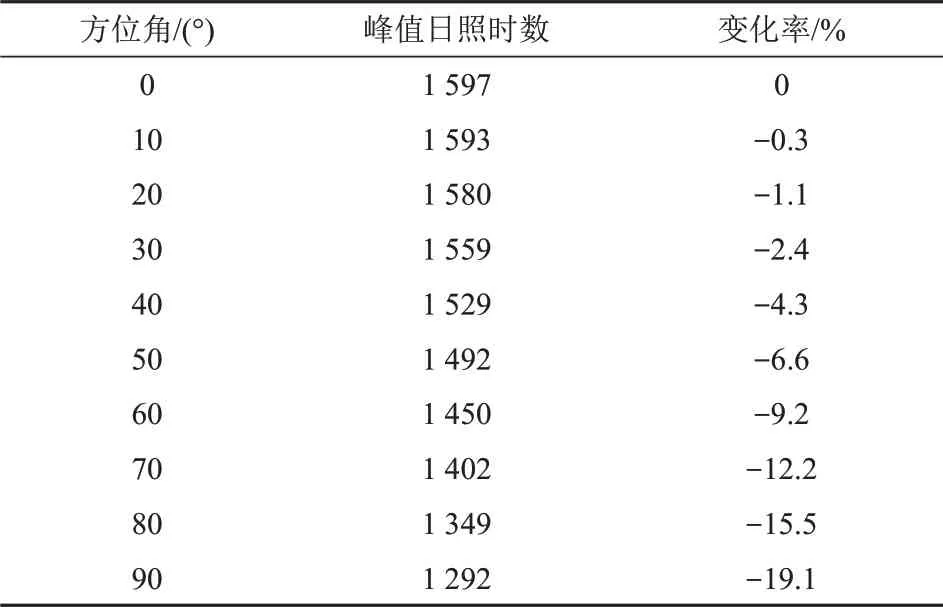
表1 方位角对峰值日照时数的影响Tab.1 Effect of azimuth on peak sunshine hours
3.2 正南倾角布置分析
对于正南倾角布置,同样使用某主流组件进行设计,各设置条件与随坡倾角布置一样,得到不同纬度、坡度下排间距随方位角变化的曲线,分别如图6、7所示。
由图6、7可见,排间距随方位角的增加而单调增加,坡度较大时,排间距增加速度更快,而坡度较小时,排间距增加速度较为平稳。
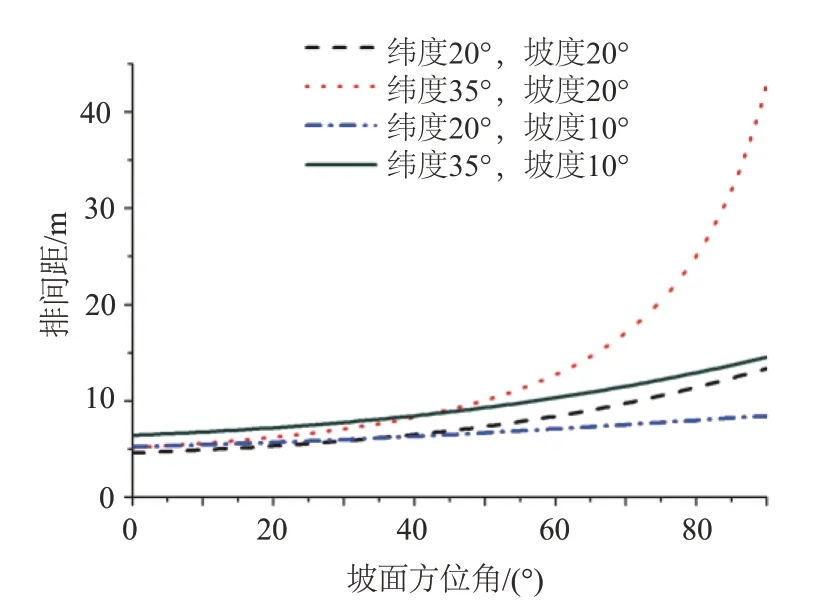
图6 中低纬度、不同坡度下排间距随坡面方位角的变化曲线Fig.6 Variation curves of row pitch with slope azimuth at low and middle latitudes and different slopes
从图7 可以看出,在方位角增大到一定数值时,计算出的排间距会陡增。通过检查和分析可知,当排间距非常大时,光线与坡面接近于平行。由此可以推测,由南向北并与坡面平行的光线穿过组件上边缘,将不会与坡面相交;当光线高度角增加一个无穷小的正值时,光线将与坡面交于北边的无穷远处,即排间距无穷大,此情况一般只会出现在坡面方位角较大时的早晨或傍晚。并且当09:00 或15:00 出现阳光先穿过坡面再穿过组件的情况时,一定在09:00—15:00 某个时刻光线无限接近平行于坡面,将会导致计算出的排间距无穷大。因此,需对2.3节中正南倾角布置的计算进行修正。更改判定条件为:当ns·nTp<0 时,

图7 高纬度、不同坡度下排间距随坡面方位角的变化曲线Fig.7 Variation curves of row pitch with slope azimuth at high latitudes and different slopes
d′pitch=+∞。
从图6 可以看出,一般在非高纬度地区,坡面方位角不大时,不易出现排间距计算值无穷大的情况。由图7可知,在纬度为50°时,坡度10°、20°、30°、40°条件下,排间距分别在方位角89°、67°、60°、56°处达到极大值。
实际上,对于方位角过大的斜坡,一味地追求高峰值日照时数,会导致较大的排间距,从而使占地增大、电缆变长,造成成本增加,得不偿失。选取方位角0°~43°,得到不同纬度、坡度下的排间距变化曲线如图8所示。通过比较同纬度、不同坡度的排间距变化曲线可以看出,在方位角较小时,大坡度的排间距比小坡度的小,然而在方位角增加到一定值时,大坡度的排间距反超小坡度的排间距,并且纬度越小,反超点对应的方位角越小(纬度20°对应反超点方位角34°,纬度35°对应反超点方位角42°)。
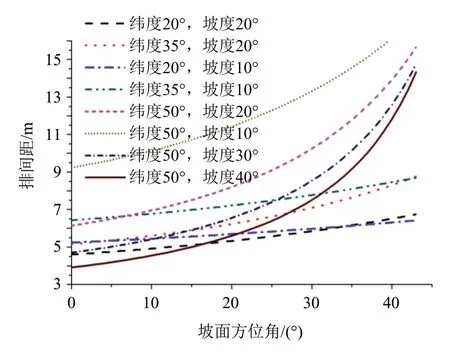
图8 不同纬度、坡度下排间距随坡面方位角的变化曲线(正南倾角布置))Fig.8 Variation curves of row pitch with slope azimuth at different latitudes and slope(south-tilt layout)
综上,光伏组件在正南倾角布置下可以得到以下结论:
1)当纬度、坡度、坡面方位角均较大时,在09:00—15:00 可能出现排间距计算值无穷大的情况。
2)当坡面方位角较大时,为获得较小的排间距,坡度不宜太大。当坡面方位角较小时,为获得较小的排间距,坡度越大越好。
3.3 2种布置方法对比
将同纬度下2 种布置方法的排间距变化曲线进行比较,结果如图9 所示。可以看出,在方位角较小时,2 种布置方法计算出的排间距相差不大,低纬度地区尤其明显;但随着方位角逐渐增大,正南倾角布置的排间距将大大增加,远大于随坡倾角布置;在低纬度地区,当坡度为10°时,随着方位角增加,正南倾角布置的排间距刚开始小于随坡倾角布置,当方位角超过30°后才逐渐大于随坡倾角布置。
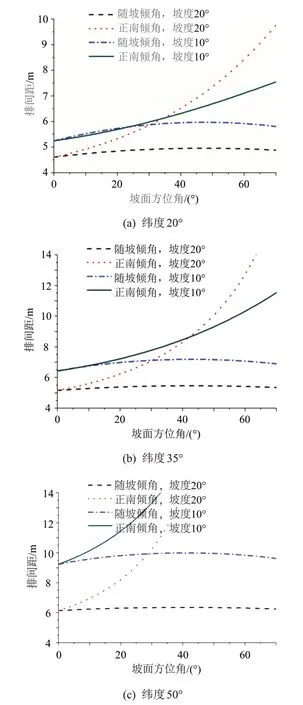
图9 同纬度下2种布置方法的排间距变化曲线对比Fig.9 Comparison of variation curves of row pitch of two layout methods at the same latitude
为直观认识正南倾角布置较随坡倾角布置的排间距更大,整理各个算例正南倾角布置比随坡倾角布置排间距大5%对应的方位角,结果如表2所示。可以看出,在中、低纬度地区,当坡度较小时,只有方位角增加至较高数值,正南倾角布置排间距才比随坡倾角布置大5%。与随坡倾角布置相比,正南倾角布置在不增加过多成本的条件下保持了较高的发电量。

表2 正南倾角布置比随坡倾角布置排间距大5%对应的方位角Tab.2 Azimuth corresponding to the row pitch at slope’s azimuth-tilt layout is 5%greater than at south-tilt layout
综上,可以得到以下结论:
1)在纬度较低(如小于35°)、坡度较小(如小于10°)、方位角较小(如小于23°)时,正南倾角布置的排间距与随坡倾角布置的相差不大,甚至很小,可在不提高成本的情况下保持较高的发电量,是有效的排布方式。
2)对于纬度稍高、坡度稍大、方位角稍大的情况,也可通过经济性比选,权衡发电量损失和成本增加,使项目收益率最大。
3)对于纬度高、坡度大、方位角大的情况,使用正南倾角布置的排间距会格外大。此时可以使用正南倾角布置,但不能按理论计算的排间距进行布置,需人为降低排间距至合适的距离,即不保证09:00—15:00 光伏组件不被遮挡,也可使用随坡倾角布置。2 种布置方法需进行详细的经济性比选,最终得出适合某个项目地且最经济的布置方法和排间距。
4 结论
对于平地光伏项目,一般计算09:00 或15:00这2 个时刻的前排影子长度,即可求出光伏阵列排间距。但山地光伏项目不然,通过分析,在正南倾角布置下,存在09:00—15:00 某个时刻计算出的排间距无穷大的情况。通过多个不同纬度、坡度、方位角的算例得出,在较低纬度、较小坡度、较小方位角的情况下,使用正南倾角布置较为合理;在稍高纬度、稍大坡度、稍大方位角的情况下,可通过经济性比选找出合适的布置方法;在高纬度、大坡度、大方位角的情况下,可调整正南倾角布置下的排间距并与随坡倾角布置进行经济性比选,最终得到合适的布置方法。

