考虑恶化效应的多目标非置换流水车间调度研究

钱伟康，唐红涛

(武汉理工大学 机电工程学院,湖北 武汉,430070)

传统的面向制造的生产调度研究中，通常假定工件的加工时间恒定。在实际生产中，由于恶化效应的影响，工件的加工时间是不确定的。恶化效应通常是由机器高负荷、作业延迟等众多因素引起的，在制造生产中普遍存在[1]。例如，在机加工过程中，机床持续工作致使刀具磨损，从而使加工时间变长；在半导体产业，处理晶圆的过程中任何延迟都需要花费额外的时间来完成[2]。因此，考虑恶化效应的调度问题更贴合实际，相对于传统调度问题也更加难以求解。

流水车间是一类典型的生产车间，广泛应用于电子、机械、化工等行业。因此，研究流水车间调度问题具有重要的工程应用价值。黎阳等[3]以最小化最大完工时间为目标，提出一种改进的模拟退火算法求解大规模的置换流水车间调度问题。刘翱等[4]针对零空闲置换流水车间调度问题，提出一种带有局部搜索的离散烟花算法。相比于上述流水车间的研究，非置换流水车间调度(non-permutation flowshop scheduling,NPFS)则允许不同机器上工件的加工顺序改变，是一类松弛置换约束条件的调度问题。郑永前等[5]以最小化最大完工时间为目标，建立数学模型和析取图模型，构造一种列表启发式算法。针对传统调度算法不能有效利用历史数据进行学习，肖鹏飞等[6]提出一种基于时序差分法的深度强化学习算法求解。尽管诸多学者对非置换流水车间进行了大量研究，然而考虑机器相关的恶化效应的文献缺乏。

智能优化算法已被证明具有解决组合优化问题的能力，且在生产调度中得到广泛应用。鲸鱼优化算法[7](whale optimization algorithm,WOA)是一种模拟鲸鱼捕食行为的群体智能优化算法。该算法原理简单，参数设置少，寻优能力强，现已成功应用于各种工程领域[8-9]。针对车间调度问题，闫旭等[10]利用量子计算与优化思想提出一种量子鲸鱼优化算法求解作业车间调度问题。栾飞等[11]对低碳车间调度问题提出一种改进的鲸鱼优化算法，算法设计了非线性收敛因子和自适应惯性权重系数来加强算法协调全局搜索和局部寻优的能力。上述研究多是对单目标进行优化求解，而实际的生产环境中常常需要考虑多个目标[12-13]，因此改进鲸鱼优化算法求解多目标调度问题具有一定的研究意义。此外，上述研究多是采用“随机键”的编码方式，虽然能实现离散值和连续值之间的转换，但不能充分利用编码中的有效信息，也不够简单易行。针对WOA算法在迭代后期种群个体均向最优个体聚集导致多样性缺失的不足，相关文献多是通过调整收敛因子以及权重来改进迭代方式，但仍以最优个体为导向进行寻优，不能完全克服迭代后期多样性缺失的问题。

考虑实际生产中机器引起的恶化效应，本文构建一个多目标非置换流水车间调度(multi-objective nonpermutation flow-shop scheduling,MONFSP) 模型，提出一种两阶段鲸鱼优化算法(TWOA)进行求解。

1 问题描述及模型构建

1.1 基于恶化效应的调度问题

Gupta等[14]首次提出具有恶化效应的生产调度问题。此后，诸多学者对生产调度领域中恶化效应模型进行了研究。现有研究中，线性恶化效应模型通常以一个根据工件的加工位置或开工时间的线性函数来描述实际加工时间[15]。然而，此类模型对某些实际问题并不适用，比如一些工件若不能在指定工期前加工才会发生恶化[16]。阶梯恶化效应模型以一个有上限的分段函数来描述实际的加工时间[17]，将实际加工时间分为基本加工时间和惩罚时间，其中基本加工时间是恒定的，惩罚时间是可变的。工件加工时不一定存在惩罚时间，只有满足一定的条件才会产生惩罚时间。另外，惩罚时间只在某区间内线性增加，达到临界值后恒定不变。因此，本文将阶梯恶化效应模型应用到流水车间调度中。图1为阶梯恶化效应的一般模型。其中p为加工时间，t为开工时间。

图1 阶梯恶化效应模型Figure 1 Step-deterioration effect model

1.2 问题描述

非置换流水车间调度问题可描述如下。n个工件在机器集M={M1,M2,···,Mm}上进行加工，每个工件经由机器M1,M2,···，Mm加工，不同机器上工件的加工顺序不相同。任一时刻每台机器只能加工一个工件，每个工件只能在一台机器上加工。进一步考虑恶化效应的影响，机器的累积工作时长超过给定的阈值下限，性能降低导致工件的加工时间增加，若超过给定的阈值上限，工件的加工时间不再增加。

作为生产系统的重要环节，最常见的调度目标是完工时间，而随着日益严格的节能减排要求，能耗也需要进一步统筹考虑。生产过程中，机器在工作状态和空闲状态单位时间能耗不一。因此，本文以最大完工时间和总能耗为优化目标。为了便于研究，相关假设如下。

1) 所有工件和机器在零时刻已准备就绪；

2) 工件一经加工便不可中断；

3) 每台机器前的等待队列容量足够大；

4) 忽略运输时间和准备时间；

5) 不同工件之间相互独立。

1.3 多目标调度模型

在不失一般性的前提下，多目标优化问题可以表示为minf(x)=min[f1(x),f2(x),···,fk(x)]，x=(x1,x2,···,xn)∈Rn。fk(x)是第k个子目标函数，x为解向量，Rn是 决策变量空间。存在解x,y∈Rn，若 ∀i，有fi(x)≤fi(y)，且 ∃i，使fi(x)＜fi(y)则 称x支 配y，记为x≺y。若解x不 被解空间Rn中任一解所支配，则称x为非劣解。所有非劣解构成的集合称为Pareto解集，记为 PF。多目标优化的目标为寻找一个均匀分布在Pareto前沿的 PF。

针对上述问题，以最大完工时间和总能耗为目标，建立多目标优化模型。相关变量的说明如表1 所示。

表1 符号Table 1 Symbols

目标函数为

约束条件为

式(1)为总的优化目标；式(2)表示最大完工时间；式(3)为总能耗；式(4)表示工件的工序约束，即同一工件的各工序之间具有先后顺序；式(5)表示机器在前一个工件的加工完成且下一个工件的上一道工序完成之后，才能进行下一个工件的当前工序的加工；式(6)表示恶化效应下工件的实际加工时间；式(7)表示工件一旦开始加工则不能被中止。

2 两阶段鲸鱼优化算法求解调度模型

2.1 基本鲸鱼优化算法原理

鲸鱼是一种具有智力的哺乳动物。有一类座头鲸的群体，由于其缺乏可以咀嚼的牙齿，只能捕食成群的小型鱼虾，从而进化出一种特殊的觅食行为。它们在收缩鱼群包围圈的同时螺旋上升吐出气泡，形成一个圆形的气幕网将分散的鱼群聚集起来完成捕食。

根据座头鲸的狩猎特点，Mirjalili等[7]于2016年提出一种新型智能优化算法——鲸鱼优化算法。

WOA提供3种个体更新方式。

1) 鲸鱼能够通过回声定位识别猎物位置并包围猎物，更新公式如式 (8) 所示。式中，g bestk表示第k代领导鲸鱼 (全局最优)的位置向量；xk和xk+1表示第k代和第k+1代个体X的位置向量。

2) 鲸鱼沿着螺旋形路径向领头鲸鱼游动，并吐出气泡形成气幕攻击猎物，更新公式如式(9)所示。式中，dist为当前个体与领导个体之间的欧氏距离；b为限定对数螺旋形状的常数；l为-1到1之间的随机数。

3) 随机搜寻。鲸鱼个体根据彼此位置进行随机搜索，更新公式如式(10)所示。式中，rand为随机选择的鲸鱼个体的位置向量；A=2ar-a；C=2r，其中收敛因子a随迭代次数从2到0线性下降，r为0～1范围内的随机向量。当|A|≥1时，算法执行第3种更新方式；当 |A|＜1时，算法随机选择前2种更新方式的一种执行。

2.2 两阶段鲸鱼优化算法

鲸鱼个体的位置更新是算法的关键。从第2.1节可以看出，WOA根据领导鲸鱼进行寻优，并通过第3种更新方式扩大搜索范围。然而，这种随机搜索的方式效率不高，此外，个体向领导鲸鱼聚集易导致群体多样性缺失从而陷入局部最优。NPFS是一个离散问题，上述更新方式也不适用于整数编码方式。对此，本文的两阶段鲸鱼优化算法设计如下。

2.2.1 编码与种群初始化

种群中的每一个体都是一个解。采用基于工件序列的整数编码方式。每个个体都是一个n维向量，每一个向量元素代表一个工件。例如，有6个工件进行加工，某个个体为X=[6,3,5,1,2,4]，表明第1个加工的是工件编号为6的工件，而优先级最低的4号工件最后加工。上述编码方式不仅简单易行，还便于计算个体所对应调度解的目标值。

初始种群的质量和多样性会影响算法的求解性能。为提高初始种群的质量，本文采用文献[18]中提出的NEH (Nawaz-Enscore-Ham)启发式算法生成一半种群规模的初始解，具体步骤如下。

步骤1计算各工件从机器M1到 机器Mm的总加工时间Ti，按降序排成序列T；

步骤2选取序列T的前2个工件，将其加入加工序列；

步骤3从未加工工件序列中随机选取一个工件，并依次插入到当前序列的所有可能位置，每插入一个位置计算该位置形成的序列的完工时间，选择完成时间最小的位置；

步骤4确定一个工件的插入位置，并从未加工工件序列中删除；

步骤5重复步骤3～ 4，直至所有工件全部插入完成。

此外，为保证种群的多样性，仍保留随机初始化策略产生剩余50%的种群个体。

2.2.2 解码与个体评价

解码是将所有待加工工件分配到各机器上，形成一个完整的可行调度方案。本文采用先到先加工(first come first served,FCFS)规则进行解码。首先，按照编码确定的工件加工顺序在第1台机器上进行加工，对于第m(m＞1)台机器，所有工件按照在前一台机器上的完成时间非降序排列依次进行加工。若多个工件的完成时间相同,则随机确定这些工件的加工顺序。

通过上述解码得到调度方案后，计算个体的目标函数值。对于多目标优化问题，不能直接比较目标函数值来评价个体的优劣。因此，本文采用文献[19]中的非支配排序来评价个体的优劣。

2.2.3 全局搜索

针对种群个体向领导鲸鱼聚集而失去多样性的问题，对鲸鱼个体的行为重新设计。首先，引入一种引导个体，该个体是指优于当前个体且距离最近的鲸鱼。领导鲸鱼和引导个体携带的猎物信息均要优于当前个体。鲸鱼个体在搜索时，根据贪婪准则执行两阶段搜索策略，个体先向引导个体移动，若获得较差的解则向领导鲸鱼移动进行捕食。两阶段的具体设计如下。

阶段1鲸鱼向引导个体U移动，获得新解X1。在寻找引导个体时从优于当前个体中选择距离最近的。通过汉明距离计算个体间的距离。汉明距离是指两个序列中位置相同值却不同的个数。例如，个体P=[2,1,3,4]和Q=[2,3,1,4]，在位置2和3处值不同，那么它们之间的距离为2。鲸鱼进行移动时若采用原更新方式会破坏编码规则，得到不可行解。对此，本文采取POX交叉算子，将交叉操作看作鲸鱼个体的移动，如图2所示。

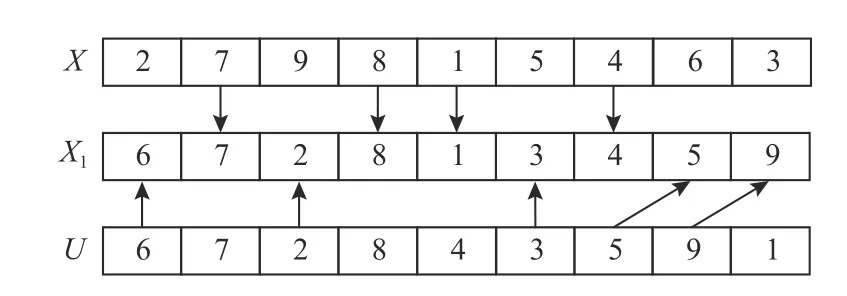
图2 POX交叉Figure 2 POX cross

以X=[2,7,9,8,1,5,4,6,3]，U=[6,7,2,8,4,3,5,9,1]为例。将工件集J={1,2,3,4,5,6,7,8,9}随机分为子集JI={1,4,7,8}和JII={2,3,5,6,9}。将X中属于JI的工件复制到X1中，保持位置不变；将U中属于JII的工件依次填入X1的剩余位置。

阶段2鲸鱼向领导鲸鱼L移动进行围捕得到新解X2。领导鲸鱼是当前全局最优个体，而在多目标问题中不能保证最优解，且为避免个体向同一领导个体聚集而失去多样性，本文从非劣个体中随机选择个体作为领导鲸鱼。此外，领导鲸鱼也是种群最靠近猎物的个体，可以将领导鲸鱼的位置视为猎物所在的位置，个体向领导鲸鱼移动即是对猎物进行围捕。个体围捕行为设计如下。

随机选取领导鲸鱼L的位置编码的一段序列D，记录D中工件在当前鲸鱼编码中的位置，对序列D中的工件随机排序，将排序后的工件依次插入记录的位置，如图3所示。

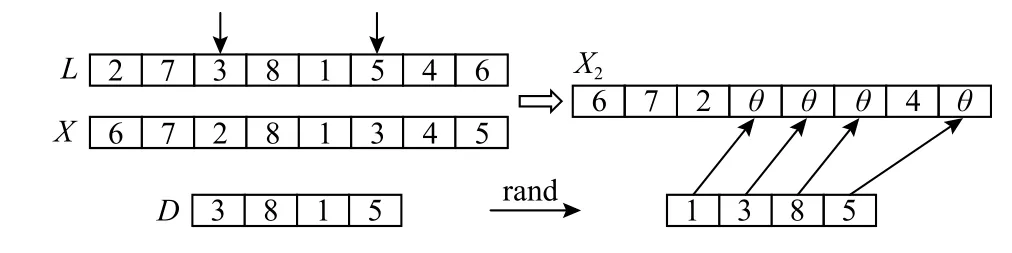
图3 围捕行为Figure 3 Predatory behavior

以领导鲸鱼L=[2,7,3,8,1,5,4,6]和 当前鲸鱼X=[6,7,2,8,1,3,4,5]为例。随机选取领导鲸鱼的编码中位置3到位置6的序列D=[3,8,1,5]，将其与鲸鱼X的编码进行比对，保留不同的工件 [6,7,2,4]，相同的工件则记为θ，将随机排序后的序列依次插入。

2.2.4 局部搜索

为提高算法的局部搜索能力，本文引入禁忌搜索机制。禁忌搜索通过禁忌表封锁搜索过的区域，以避免重复搜索，保证搜索的多样性。故禁忌表的长度在很大程度上影响搜索效率和解的质量。本文采用随迭代周期动态变化的禁忌表长度，计算公式如式 (11)所示。其中，w为工序数，k为当前迭代次数，λ =MaxIt/5，M axIt为最大迭代次数。

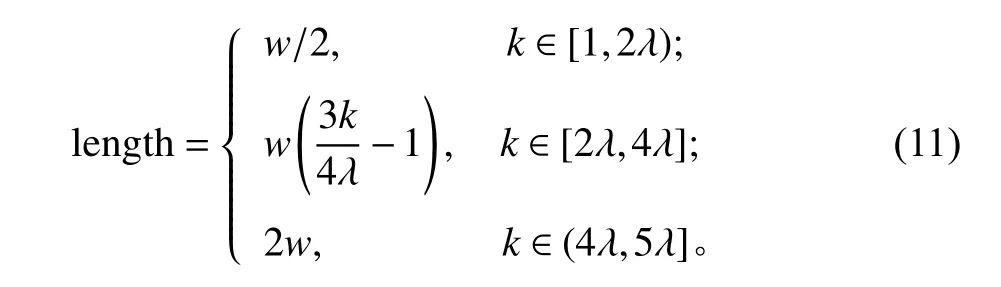
邻域结构对禁忌搜索的质量和执行效率也有较大的影响。本文采用3种有效的邻域结构，即基于NEH的插入邻域、交换邻域和逆向邻域。3种邻域的具体操作如下。

1) 基于NEH的插入邻域。在个体序列中随机选择一个位置将其插入到序列的所有可能位置，计算插入后序列的完工时间，获得所有完整序列中的非劣解。例如，某个体X=[5,1,2,3,4,6]，随机选择位置2，共有6个可能插入的位置，计算这6种插入后的完整序列的目标，取其中的非劣解。

2) 交换邻域。在个体序列中随机选择两个不同的位置，交换两个位置上的元素。例如，某个体X=[5,1,2,3,4,6]，随机选择位置2和位置5进行交换操作得到个体X=[5,4,2,3,1,6]。

3) 逆向邻域。在个体序列中随机选择两个不同的位置，将两位置间的子序列逆向。例如，某个体X=[5,1,2,3,4,6]，随机选择位置2和位置5进行逆向操作得到个体X=[5,4,3,2,1,6]。

局部搜索的具体步骤如下。

步骤1获取个体解，禁忌表；

步骤2通过邻域结构生成邻域解，计算其目标值，删除在禁忌表中存在的邻域解；

步骤3若有邻域解支配当前解，则更新当前解；

步骤4若存在邻域解与当前解不相互支配，则随机选择互不支配的邻域解；

步骤5若没有邻域解支配当前解，则保持当前解；

步骤6更新禁忌表，若禁忌表已满则删除最先加入禁忌表的个体，结束。

算法整体流程如图4所示。

图4 TWOA算法流程图Figure 4 TWOA flow chart

3 仿真实验

3.1 测试算例及性能指标

参考文献[1]中的设计并结合1.3节的调度模型，测试算例设计如下。考虑工件数n={10,20,40,60,80}和机器数m={5,8,10}，共15个算例。各工件在各机器上的加工时间在[0.5 h,3 h]上服从离散均匀分布；各机器的恶化率在[0.05,0.10]上服从离散均匀分布，阈值下限在[8,21]上服从离散均匀分布，阈值上限在[55,70]上服从离散均匀分布；各机器处于工作状态时，单位能耗在[2 kW,5 kW]上服从离散均匀分布，处于空闲状态时单位能耗在[0.5 kW,1 kW]上服从离散均匀分布。

由于是多目标算法之间的比较，本文引入3个衡量多目标算法性能的指标，分别为收敛性指标GD[20]、多样性指标Δ[21]和综合性指标I GD[22]。

GD表示非劣解集PF的收敛程度，计算公式如式(12)所示。式中，P F*为 净最优Pareto解集；N为PF中的个体数；dist(xi,PF*)表 示PF中个体xi与 PF*个体之间的最小欧氏距离。G D值越小，算法收敛性越好。

Δ表示非劣解集PF的分布情况，计算公式如式(13)所示。式中，df和dl是PF*的极端解和PF的边界解间的欧氏距离；di为PF中第i个体与最近个体之间的欧氏距离；d为di的 平均值。Δ值越小，算法得到的非支配解分布越均匀。

IGD代表算法的综合性能，计算公式如式(14)所示。式中M为 PF*中 的个体数；dist(y,PF)表 示 PF*中个体y与PF个体之间的最小欧氏距离。I GD值越小，算法的综合性能越高。

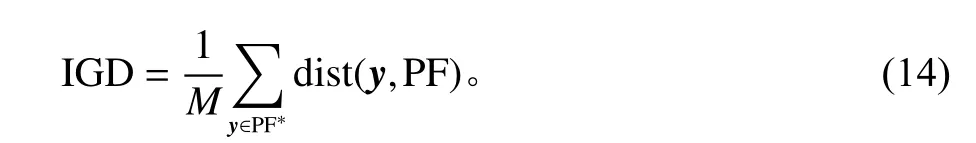
3.2 对比实验及结果分析

为了验证TWOA算法求解上述模型的可行性和有效性，选择经典的遗传算法(genetic algorithms,GA)、变邻域搜索算法(variable neighborhood search,VNS)以及文献[11]提出的IWOA算法进行对比实验研究。其中，GA作为经典的智能算法，已成功地用于解决各种调度问题。VNS具有优秀的局部搜索能力。IWOA则是WOA在车间调度领域的一种改进算法。首先，采用正交实验设计法对TWOA算法的参数进行优化选取，经多次组合实验确定如下参数。种群大小为80，最大迭代次数为100。3种对比算法采用随机初始化方法，其余参数均采用来源文献中的设置。此外，GA采用POX交叉算子，VNS采用2.2.4节所描述的3种邻域结构。

各算法均使用Matlab R2016a编程实现，并在Intel Core i5，2.60 GHz CPU，4 GB RAM和Windows 7 操作系统的环境中运行。各算例均独立运行20次，且每次运行的终止时间设为80 s。实验结果如表2、3所示。可以看出，在小规模算例上，各算法取得的最优值在同一水平，但TWOA的均值更小，这表明其稳定性高于其他算法。而随着规模的增大，TWOA获得的解的质量全面优于另外3种算法。综合来看，本文提出的算法优于其他3种算法。

表2 实验结果—最小值Table 2 Experimental results-minimum

3种指标的均值统计结果如图5～ 7所示。可以看出，在小规模问题上，VNS的性能更优。而随着问题规模的增大，TWOA的收敛性、多样性和综合性能都比其余3种算法好，进一步验证了该算法对求解阶梯恶化效应的车间调度模型的可行性及有效性。这表明，本文的初始化策略能保证种群多样性的同时提高个体质量，而两阶段搜索策略能更好地避免多样性缺失，有效的3种邻域结构帮助个体跳出局部最优，且长度动态变化的禁忌表能提高局部搜索的效率。

图5 GD对比折线图Figure 5 The comparison in terms of GD

表3 实验结果—均值Table 3 Experimental results-means

4 结语

基于流水车间，考虑实际加工中机器长时间运行引起的恶化效应，本文构建一个以最大完工时间和总能耗为目标的阶梯恶化效应调度模型。为求解该模型，提出一种两阶段鲸鱼优化算法(TWOA)。算法采用NEH启发式算法提高初始种群的质量，在种群寻优过程中，设计一种基于引导个体和领导个体的两阶段全局搜索策略。这种策略能更好地克服个体聚集致使多样性缺失的缺点。同时，一种禁忌表长度动态变化的禁忌搜索机制的嵌入有利于减小算法陷入局部极值的概率。最后，通过对15种不同规模的测试算例进行对比实验，结果表明，对于大规模算例，该算法对求解阶梯恶化效应调度模型的性能更优。

图6 Δ对比折线图Figure 6 The comparison in terms of Δ

图7 IGD对比折线图Figure 7 The comparison in terms of IGD