农机装备上下游企业质量投入博弈分析研究

李洪波，张欣璞，史 欢

(江苏大学 1.管理学院；2.中国农业装备产业发展研究院，江苏 镇江 212013)

近年来，中国农机装备制造产业在国家政策的大力扶持下得到了快速发展，已成为世界第一制造与使用大国，但产品质量问题仍然不容乐观[1]。由国家质检总局和市场监管总局近年发布的产品抽查情况(国质检监函〔2017〕105、408、632号，国市监质监函〔2019〕40号)来看，稻麦联合收割机、植保机械等多种农业装备，以及单缸柴油机零部件产品因质量问题被予以通报。而农机装备作为农业生产的物质技术基础，农业现代化的发展离不开高质量的农机装备供给。为此，国务院出台的《关于加快推进农业机械化和农机装备产业转型升级的指导意见》中明确提出要推动农机装备产业高质量发展，加强农机装备质量与可靠性建设。由于农机质量不仅受到整机架构以及装配质量的影响，还依赖于上游农机零部件商所提供的零部件质量，这就要求农机装备上下游企业不但要根据农业生产的实际要求改进产品设计，还要在后续制造环节中加强质量控制。因此，需要同时审视农机零部件商与整机制造商的质量行为，他们对质量的投入及协调关系是提升农机产品整体质量水平的关键。

当前，围绕农机装备质量的研究大多集中在质量评价、提升路径以及政策效应等方面。1) 质量评价方面。周晨等[2]从宏观层面对我国农机质量整体水平进行了评价，认为我国农机装备质量水平与发达国家差距较大，尤其是机器的可靠性程度方面。周晶等[3]则通过在华中地区对农机户开展农机产品质量满意度评价研究，从微观层面评估了国产农机装备的可靠性与适用性，并指出国产农机产品需在产品设计以及硬件配置方面进一步改进。2) 提升路径方面，加强农机生产企业技术研发水平和自主创新能力是提升中国农机装备质量水平的关键已达成共识。如刘芳等[4]测度不同农机装备企业的产品质量提升效率，得到农机生产企业应加强技术研发投入以及规范技术标准的结论。刘勤[5]通过对比分析全球农机装备专利技术信息，发现加大核心技术的研发投入是提升农机装备质量水平的重要途径。颜廷武等[6]结合技术发展和土地制度的变革对农机工业的影响，认为建立适合中国的农机创新体系是实现农机工业高质量发展的根本路径。3) 政策效应方面。王许沁等[7]认为农机补贴政策有利于农机装备质量的提升，但这种积极作用随着时间推移而逐渐变弱。潘彪等[8]构建四方博弈模型，剖析了农机购置补贴的政策效果，指出补贴进口农机产品有利于提高国产农机产品质量水平。然而，有学者对购机补贴政策的积极作用产生质疑。周应恒等[9]采用随机前沿模型实证发现农机购置补贴政策未必能够促进农机工业的技术创新。蔡海龙等[10]认为购机补贴政策会给农机生产企业为进入推广目录创造寻租空间，无助于产品质量的保证，却在一定程度上扭曲了市场竞争机制。

综上，学界针对农机装备质量问题的研究颇为丰富，且呈现出以宏观的面板数据分析或实证分析为主，而从农机装备产业链内部企业主体微观视角的研究较少。由于农机产品质量形成具有事先性与动态性，时间变量是影响双方质量投入决策的重要因素。微分博弈理论作为处理连续时间内多决策主体之间协调控制问题的重要模型，在研究供应链上下游决策主体间的竞合问题上应用较为广泛。如Chutani等[11]基于微分博弈理论，研究由独立制造商和零售商组成的市场中动态合作广告决策问题。Guan等[12]通过建立由上游制造商和下游再制造商组成的微分博弈模型，解决具有纳什议价公平性的供应链协调问题。Xiang等[13]基于微分博弈理论，构建了由一个制造商和一个供应商组成的两阶段闭环供应链动态模型。

针对当前缺少从微观视角对农机零部件商与整机制造商的质量投入行为建模决策分析的现状，本文拟利用微分博弈模型，分析农机装备上下游企业在无成本分担与有成本分担Stackelberg博弈，及协同合作博弈3种情形下的动态决策过程，寻求影响供需质量投入的关键因素，设计针对质量投入的协调机制，以期为零部件商和整机制造商质量投入的努力水平、激励问题以及合作契约设计等方面提供决策支持。

1 问题描述与假设

本文仅考虑由一个农机零部件商(S)和一个整机制造商(M)组成的二级农机供应链。由于设计和制造是农机产品质量形成过程的关键环节，因此本文重点研究农机零部件商和整机制造商在设计和制造两个环节中的质量投入行为。1) 在设计环节，农机整机制造商的质量投入主要包括根据实际农业生产要求对农机整体结构进行合理设计及改进；农机零部件商根据设计方案提取结构参数和关键质量特性对零部件进行优化设计。2) 在制造环节，农机零部件商的质量投入包括提升工艺水平提高加工质量；整机制造商通过引进先进制造技术或设备升级等措施提升整机的装配质量。为建模需要，作出如下基本假设。

假设1农机零部件商和整机制造商均属于经济理性人，即各自追求自身利益的最大化，且双方的成本及利润已知。

假设2考虑农机产品的质量提升由零部件商和整机制造商在设计与制造环节质量投入的努力水平决定，参考文献[14]，假设农机产品质量的动态方程为

其中，Q(t)表 示时刻t农机产品质量，且初始质量Q0=Q(0) ；S1(t)、S2(t)分别表示农机零部件商在设计和制造环节质量投入的努力水平，且 α1、α2分别表示在两个环节质量投入的努力水平对农机产品质量的影响系数；M1(t)、M2(t)分别代表整机制造商在这两个环节中质量投入的努力水平，且 β1、β2分别表示在两个环节质量投入的努力水平对农机产品质量的影响系数；δ为农机产品质量的相对衰减率。

假设3考虑成本函数存在边际递增性，借鉴文献[15]，假设零部件商和整机制造商双方的质量投入成本函数分别为。kS1、kS2、kM1、kM2均为大于零的常数，分别表示农机零部件商和整机制造商在设计以及制造环节质量投入的成本系数。

假设4考虑零部件商和整机制造商质量投入所产生的收益与农机产品质量水平成正比，假设农机供应链的总收益是农机产品质量的线性函数，表示为

其中，μ和 φ均 为大于零的常数；φ为农机产品质量对供应链整体收益的影响程度。

假设5零部件商和整机制造商按照一定比例分配农机供应链总收益，零部件商获得 ω，整机制造商获得1 -ω。其中，ω ∈(0,1)为分配系数，是双方在一定范围内协商确定的常数。

本文所构建的模型控制变量包括：S1(t)、S2(t)、M1(t)、M2(t)。设计与制造环节的成本分担比例为 θ1(t)与 θ2(t)，以及一个状态变量Q(t)。其余参数均为与时间无关的常数，为方便书写，下文都将省略时间t。

2 模型构建与求解

2.1 无成本分担Stackelberg博弈模型

在此情形下，整机制造商作为农机供应链的核心企业不愿为农机零部件商分担任何成本。整机制造商首先决定自身的最优质量投入策略，农机零部件商观察到整机制造商的决策后选择自己的最优策略。此时，双方的目标函数分别为(其中 ρ表示折扣因子)

命题1农机零部件商与整机制造商在无成本分担Stackelberg博弈中双方的最优策略为(上标用A表示)

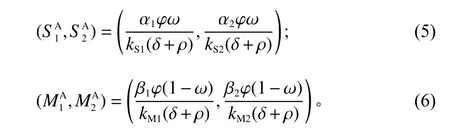
证明此情形下整机制造商和农机零部件商的博弈过程可视为Stackelberg博弈，可采用逆向归纳法求解。根据最优控制解法，零部件商的收益(VS(Q))满足HJB方程 (Hamilton-Jacobi-Bellman equation)。

根据最大化的一阶偏导数条件，得

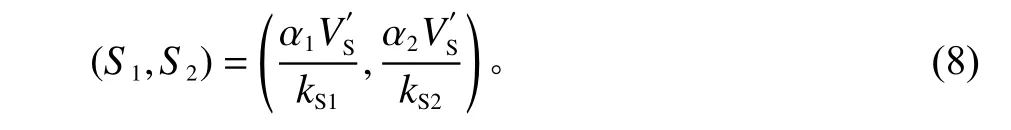
整机制造商的收益(VM(Q))满足HJB方程

将式(8)代入式(9)后对 (M1,M2)求一阶偏导数，并令其等于零得

将式(8)、式(10)代入式(7)和式(9)，整理得

由式(11)、式(12)可见，关于Q的线性最优值函数是HJB方程的解。因此，令

其中，a′、b′、c′、d′为待定常数。将式(13)及其他对Q的导数代入式(11)和式(12)，得到

命题1得证。该条件下农机零部件商、整机制造商和农机供应链的最优收益分别为

2.2 成本分担Stackelberg博弈模型

在此情形下，整机制造商首先决定自身的最优质量投入策略，并确定承担农机零部件商在设计和制造环节质量投入成本的比例 θ1、θ2(θ1,θ2∈[0,1])。此时，双方的目标函数分别为

命题2农机零部件商和整机制造商在成本分担Stackelberg博弈中，双方的最优策略为(上标用B表示)

证明该命题证明步骤与情形A类似，故省略。该情形下农机零部件商、整机制造商和农机供应链的最优值函数为

2.3 协同合作博弈模型

在此情形下，农机零部件商与整机制造商作为一个有机整体，以农机供应链整体收益为最大化，共同确定最优质量投入。因此，农机供应链的目标函数为

命题3农机零部件企业和整机制造商在协同合作博弈中，双方的最优策略为(上标用C表示)

根据最大化的一阶偏导数条件得农机零部件商和整机制造商的最优策略为

由式(32)可见，关于Q的线性最优值函数是HJB方程的解。因此，令

其中，a′′、b′′为待定常数。将式(33)及其他对Q的导数代入式(32)，得到

把V′=b′′代入式(30)和式(31)，得到农机零部件商和整机制造商最优策略。

由此命题3得证。该情形下农机供应链的最优收益为

2.4 比较分析

结论1从无成本分担Stackelberg博弈情形到成本分担Stackelberg博弈情形，整机制造商作为农机供应链的主导者，在设计与制造环节质量投入的努力水平保持不变；但整机制造商对农机零部件商的成本分担可使零部件商在设计与制造环节质量投入的努力水平得到提升。

结论2在协同合作博弈中，农机零部件商和整机制造商在设计与制造环节质量投入的努力水平高于其他两种博弈情形。

证明根据式(5)、(6)、(19)～ (22)、(27)、(28)，可得 (其中ω ＜0.67)

由 式(36)～ (38)可 知，结论1得 证；由(39)、(40)得可知，结论2得证。

结论3从无成本分担Stackelberg博弈情形到成本分担Stackelberg博弈情形，农机产品的质量水平得到提升。而在协同合作博弈中，随着双方在设计与制造环节质量投入的努力水平达到最高，农机产品的质量水平达到了最高。

证明根据式(36)～ (40)可得(其中ω ＜0.67)

结论4从无成本分担Stackelberg博弈到成本分担Stackelberg博弈的转变，农机零部件商与整机制造商以及农机供应链的最优收益均增加，从而实现了Pareto改进。

结论5在协同合作决策情形下，农机供应链的整体收益水平最高。

证明根据式(16)～ (18)、(23)～ (25)、式(35)可得(其中ω ＜0.67)

由式(41)～ (43)可知，结论4得证；由式(43)、式(44)可知，结论5得证。

结论6收益分配系数 ω的取值存在一个合适范围使得协同合作对于农机零部件商与整机制造商是Pareto最优的，即实现双方质量投入行为的协调。

证明：协同合作情形下，农机零部件商和整机制造商将按照 ω和 1 -ω的比例分配农机供应链整体收益，可得

由结论5可知，协同合作博弈情形下农机供应链的总收益最高，如果农机零部件商和整机制造商在协同合作博弈情形下各自的最优质量投入所获收益高于其他两种博弈情形，则对于双方来说，协同合作博弈是Pareto最优。由此得到如下条件。

3 算例分析

基于上述模型的分析结果，运用Matlab R2018a对其进行算例仿真分析。参考文献[15]部分参数取值并结合实际情况，假设 ρ=0.1，α1=0.5，α2=0.4，β1=0.4，β2=0.2，δ=0.1，kS1=0.6，kS2=0.4，kM1=0.4，kM2=0.3，μ=1，φ =0.5，Q0=3。

图2 收益分配系数ω对整机制造商收益的影响Figure 2 The influence of income distribution coefficient ω on the revenue of the complete machine manufacturer

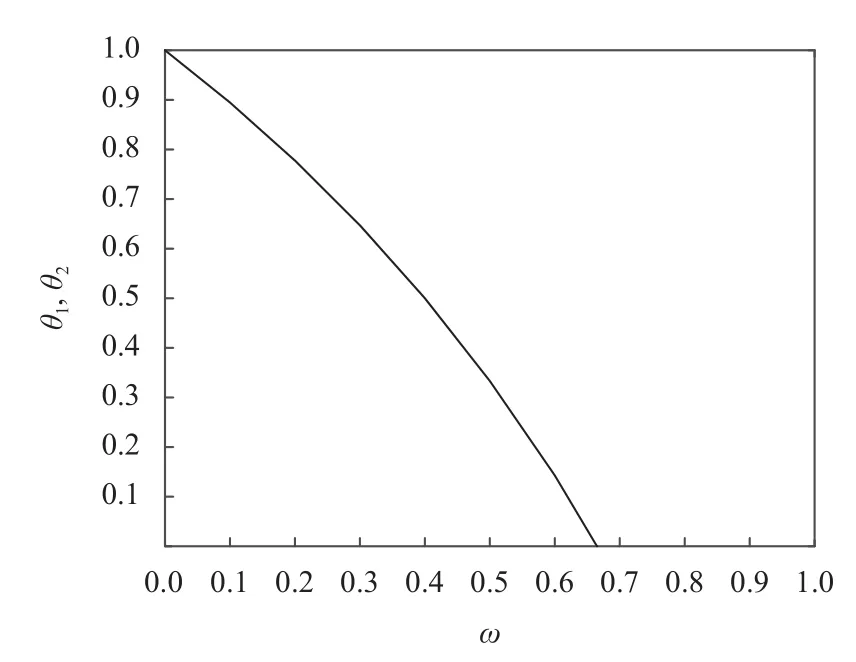
图3 收益分配系数ω对成本分担系数的影响Figure 3 Influence of income distribution coefficient ω on cost sharing coefficient

1) 考虑农机零部件商和整机制造商是追求自身利益最大化的理性个体，因此在质量投入之初(取t=0)选择以何种形式展开质量投入的前提是实现各自的利润增加。由图1～ 3可以得到如下结果。(1) 当收益分配系数 ω在一定范围(ω ＜0.67)内，成本分担Stackelberg博弈情形下农机零部件商的收益高于无成本分担Stackelberg博弈情形。(2) 在成本分担Stackelberg博弈情形下，整机制造商虽然承担了额外成本，但收益仍高于无成本分担Stackelberg博弈情形。(3) 当 ω ＜0.67时，整机制造商对农机零部件商在设计与制造环节质量投入成本的分担比例不为零，这是因为制造商作为农机供应链中的核心企业，如果自身所占收益比例太小，会因无法实现自身的Pareto改进而失去激励零部件商质量投入的积极性。(4) 存在合适的收益分配系数(ω ∈[0.36，0.67))使农机零部件商与整机制造商在协同博弈情形下的收益高于其他两种情形，即实现双方个体的Pareto最优。上述结论与前文理论推导结果一致。

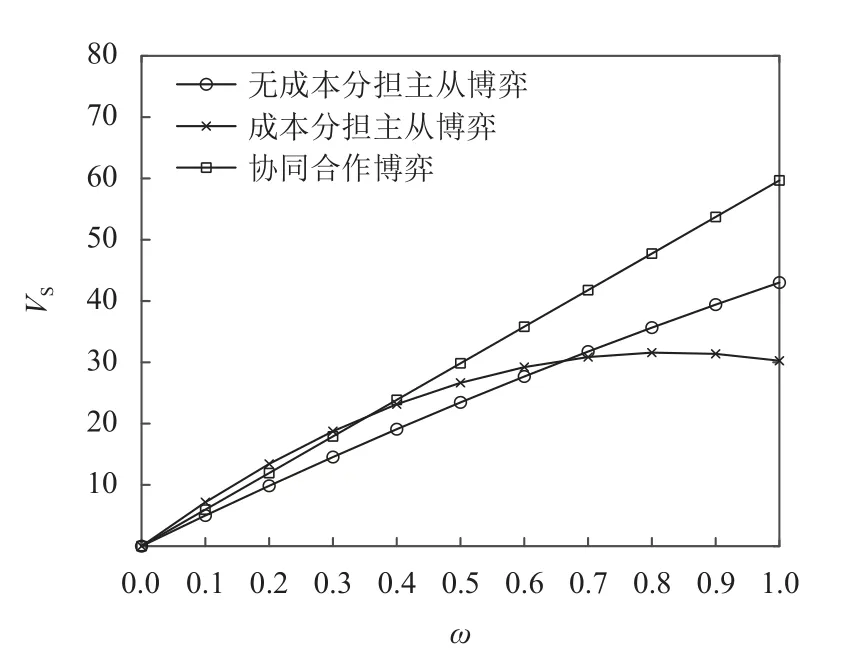
图1 收益分配系数ω对农机零部件商收益的影响Figure 1 Influence of income distribution coefficient ω on the income of agricultural machinery parts suppliers

2) 通过将参数代入命题1、命题2和命题3，且取 ω=0.4(ω ∈[0.36，0.67)) 得：=(0.83,1.00)，=(1.67,2.00)，，=(2.08,2.50)=(1.50,1.00)，=(1.50,1.00)，=(2.50,1.67)。由上述结果可知：成本分担Stackelberg博弈情形下的农机零部件商的质量投入的努力水平相比于无成本分担Stackelberg博弈情形得以提升，这是由于农机整机制造商分担部分零部件商的质量投入成本会对农机零部件商产生一定的激励作用，但并不会改变自身质量投入的努力水平；而在协同合作博弈情形下，双方质量投入的努力水平都得到了提升。

3) 由图4可知，零部件商与整机制造商长时间在设计与制造环节对质量的不断投入，农机产品质量水平得到提升，而质量水平随着质量衰减系数而降低；成本分担Stackelberg博弈情形下的农机质量水平优于无成本分担Stackelberg博弈情形下的质量水平；在协同合作博弈情形下，由于双方共同积极致力于质量投入，农机质量水平达到了最优。

图4 农机产品质量水平比较(ω=0.4)Figure 4 Comparison of quality levels of agricultural machinery products (ω=0.4)

图6 整机制造商收益比较(ω=0.4)Figure 6 Income comparison of complete machine manufacturers (ω=0.4)

图7 农机供应链整体收益比较(ω=0.4)Figure 7 Overall income comparison of agricultural machinery supply chain (ω=0.4)

4) 由图5～ 7可得如下结果。(1) 在无成本分担和成本分担Stackelberg博弈，及协同合作3种博弈情形下，农机零部件商与整机制造商的收益随着时间的推移而增加，而随着农机质量水平自然下降速度增大，双方收益均下降。因此，从长远来看，无论农机装备上下游企业选择何种形式进行质量投入都应该注重农机产品质量提升，只有提升农机质量水平才能获得更高收益。(2) 对于农机零部件商、整机制造商以及供应链整体收益来说，从无成本分担Stackelberg博弈情形到成本分担Stackelberg博弈情形再到协同合作博弈情形的转变，是一种Pareto改进。

图5 农机零部件商收益比较(ω=0.4)Figure 5 Income comparison of agricultural machinery parts suppliers (ω=0.4)

4 结论

本文利用微分博弈，分析了农机零部件商与整机制造商在质量形成过程中设计与制造两个关键环节中的质量投入决策，分别求得了在无成本分担和有成本分担Stackelberg博弈，及协同合作博弈3种情形下的均衡结果，得到以下结论。1) 3种博弈情形下，农机零部件商和整机制造商努力水平与质量投入成本系数成负相关，与质量影响系数以及质量收益系数成正相关。2) 整机制造商对零部件商的成本分担可有效提高零部件商在设计和制造环节质量投入的努力水平，而在协同合作博弈情形下双方在设计和制造环节质量投入的努力水平达到了最高。3) 整机制造商通过对零部件商的成本分担，可以促进农机产品质量水平的提高，并且在协同合作博弈情形下，农机装备质量水平达到了最高。4) 在协同合作博弈情形下，收益分配系数 ω在合适的范围内可实现农机零部件商和整机制造商双方个体收益以及农机供应链整体收益的最优，从而实现双方质量投入行为的协调。

研究对提升我国农机装备高质量发展的现实意义是：1) 政府可以对农机上下游企业在质量投入方面进行补贴以降低成本，提高零部件商与整机制造商质量投入的积极性；2) 政府在制定产业政策时一方面应注意引导处于供应链核心地位的整机制造商发挥对零部件商的激励作用，另一方面要积极促进农机装备上下游企业建立合作关系；3) 为实现农机装备上下游企业在质量投入方面长期稳定的合作关系，双方在签订契约时应综合考虑各自的资源投入、收益等因素，进而确定一个合理的收益分配系数。

此外，本文在讨论协同合作博弈情形下农机装备上下游企业质量投入行为的协调时，虽然讨论了收益分配系数的范围，但并未给出具体数值，后续研究可进一步对最终利益分配系数的确定进行讨论分析。