基于Adam算法优化GRU神经网络的短期负荷预测模型

高 翱，李国玉，撖奥洋，周生奇，魏 振，张智晟

（1.青岛大学电气工程学院，山东青岛 266071；2.青岛地铁集团有限公司，山东青岛 266000；3.国网青岛供电公司，山东青岛 266002）

随着电网复杂性的增加，电力系统对电力供需 实时平衡提出了更高的要求[1-2]。准确的短期负荷预测可以帮助电网工作人员制定准确合理的生产计划，维持供需平衡，保证电网安全运行[3-5]。

利用神经网络模型进行负荷预测属于智能预测法。文献[6]采用改进的粒子群算法优化循环神经网络（RNN），但是RNN 容易出现梯度消失和梯度爆炸现象。文献[7]提出了一种基于卷积神经网络和长短期记忆神经网络的预测方法，LSTM 神经网络解决了循环神经网络中存在的梯度消失和梯度爆炸的问题，但是在运行时，计算量偏大，计算时间偏长。文献[8]提出了一种CNN-GRU 混合神经网络，利用CNN 提取特征向量，将其输入到GRU 神经网络中进行训练，在提高预测精度的同时，也加快了模型的训练速度。

该文采用Adam 算法优化GRU 神经网络模型，不仅解决了RNN 模型中存在的梯度消失和梯度爆炸的问题，而且解决了LSTM 模型中存在的收敛速度较慢的问题。Adam 算法有效解决了随机梯度下降算法前期收敛速度慢和容易产生精度下降的问题。以某地区的实际电网负荷数据为例，对该文提出的模型进行仿真验证，证明了该模型能够有效提高短期负荷预测的准确性。

1 GRU神经网络

GRU是在LSTM神经网络的基础上提出来的[9-10]。LSTM 神经网络由输入门、遗忘门、输出门组成[11-12]，GRU 将LSTM 的遗忘门和输入门合并成更新门，同时将记忆单元与隐含层合并成重置门，进而让整个结构运算变得更加简化且性能得以增强[13-15]。GRU结构图如图1 所示。

图1 GRU结构图

图1 中：xt为t时刻的输入；ht-1为t-1时刻的输出；zt为更新门，rt为重置门；为t时刻隐含层的激活状态；ht为t时刻的输出。σ为sigmoid函数，可以将数据限制在0～1 范围内；tanh 激活函数将数据放缩到-1～1 范围内；⊕代表进行矩阵加法操作；⊗代表矩阵之间按元素相乘，要求相乘两个矩阵是同型的；1-表示运算后的输出为1-zt。

GRU 可由下式描述：

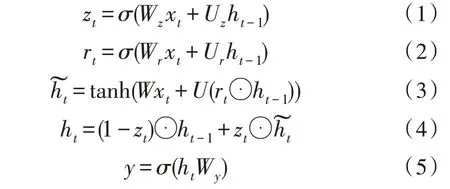
其中，Wz、Uz、Wr、Ur、W、U、Wy为GRU 神经网络的权值，W为输入层到隐含层的权值，U为隐含层自身的权值，Wy为隐含层到输出层的权值，Wz为输入到更新门zt的权值，Uz为上一时刻隐含层到更新门zt的权值，Wr为输入到重置门rt的权值，Ur为上一时刻隐含层到重置门rt的权值，y为神经网络的输出，⊙表示矩阵中对应的元素相乘。

2 基于Adam算法优化GRU神经网络

常规的GRU 神经网络采用随机梯度下降算法迭代更新神经网络的权重，此模型算法前期的收敛速度较慢，而且容易出现精度下降的问题。为了提高预测的精度，加快模型前期的收敛速度，文中采用Adam 优化算法并引入学习率衰减策略，对GRU 神经网络模型进行优化。

2.1 Adam优化算法

Adam 通过计算梯度的一阶和二阶矩估计为不同的参数设计独立的自适应性学习率[16]。

其算法如下：

首先，计算mt和vt的衰减平均值：

一阶矩估计：

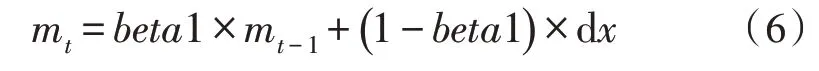
二阶矩估计：

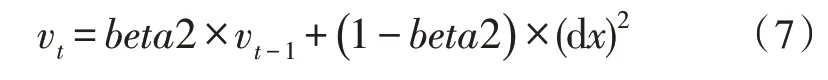
其中，beta1 为一阶矩估计的指数衰减率；beta2为二阶矩估计的指数衰减率，dx为梯度。该文令参数beta1=0.9，beta2=0.999。

第二步进行偏差修正，通过计算偏差，修正了第一和第二矩估计。

一阶矩估计、二阶矩估计偏差修正：

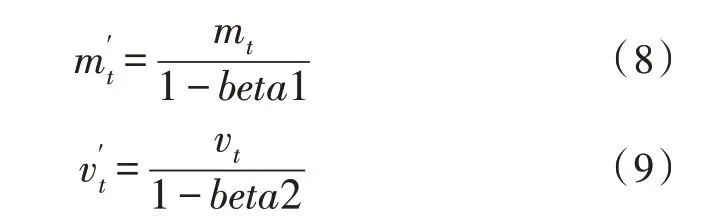
参数更新：

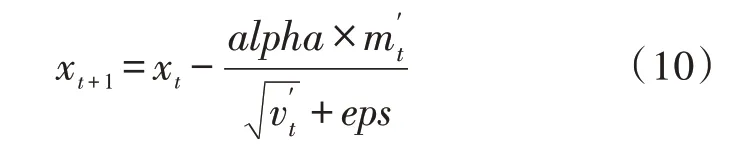
其中，xt、xt+1为参数向量，参数eps是一个接近于0 的正数，可以防止公式计算中分母为0；alpha代表学习率。eps=1×10-8，且参数eps的初始值为0。

2.2 Adam算法中的学习率衰减策略

该文在Adam 算法的基础上引入了学习率衰减策略[17]，可以加快参数的更新速度，使Adam 算法在前期的收敛速度加快，并且可以提升模型的精度。

该文采用的是分数衰减方式，分数衰减的公式为：

其中，epoch代表样本集内所有的数据经过了一次训练；decayrate为衰减率。文中令参数decayrate=1，epoch=1。

随着迭代次数的增加，学习率将以分数衰减方式衰减，通过衰减后的学习率寻求全局最优解。采用此方法的目的是希望减少迭代过程中收敛曲线的振荡，提高模型收敛速度和稳定性，得到全局最优解。

为了避免出现采用学习率衰减策略时学习率衰减到零的情况，令最小学习率为0.000 5。在算法迭代过程中，当学习率小于0.000 5 时，将不再进行学习率衰减。

3 算例分析

3.1 数据处理

为了验证该文模型的有效性，将某地区实际电网负荷数据作为算例进行预测仿真，预测日负荷96个点的数据。

该文采用了15 维的输入变量。要预测某天t时刻的负荷数据，需要考虑15 维的输入变量，包括预测日前3 天的t-1 时刻、t时刻、t+1 时刻的负荷数据（共9 维），以及预测日当天的最低气温、最高气温、平均气温、天气因素、降水概率、日类型（共6 维）。为了使输入数据的量纲统一，对输入数据采用归一化处理，即：

其中，X为归一化处理之后的输入数据；x为实际的输入数据；xmax为实际输入数据的最大值；xmin为实际输入数据的最小值。

3.2 仿真结果分析

基于Adam 算法优化的GRU 神经网络模型采用15-10-1 结构。输入维数是15 维，隐含层神经元个数为10 个，输出维数为1 维。模型的初始学习率alpha0=0.6，经学习率衰减后的最小学习率为0.000 5。最大迭代次数为8 000 次，在训练过程中，当预测值与实际值误差小于0.05%时，终止循环，将此时的权值赋给GRU 神经网络。

为了验证学习率衰减策略能提高预测的精度，将采用学习率衰减策略的Adam 算法优化GRU 神经网络的模型与不采用学习率衰减策略的Adam 算法优化GRU神经网络的模型进行对比分析，如图2所示。

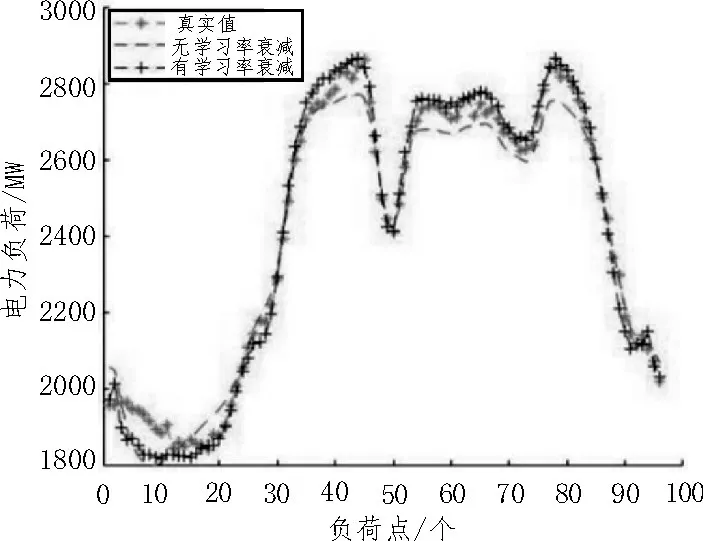
图2 有无学习率衰减策略的Adam-GRU 模型负荷预测对比图

采用平均绝对百分比误差EMAPE和最大相对误差Emax来评估模型的预测效果。EMAPE如式（13）所示：

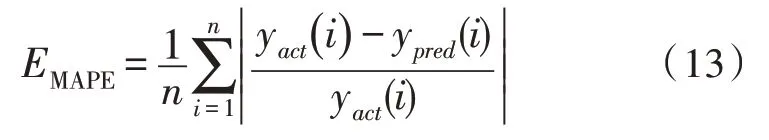
其中，n为预测负荷点的总个数；yact(i)为i时刻负荷的真实值；ypred(i)为i时刻负荷的预测值。

由图2 可知，不采用学习率衰减策略的Adam-GRU 负荷预测模型的EMAPE为1.78%，Emax为6.46%；采用学习率衰减策略的Adam-GRU 负荷预测模型的EMAPE为1.40%，Emax为5.38%。由此可知，学习率衰减策略有效提升了模型的预测精度。

为了验证基于Adam 算法优化GRU 神经网络的短期负荷预测模型的有效性，将该模型与BP 神经网络模型和GRU 神经网络模型进行对比研究分析。3 种模型的负荷预测对比图如图3 所示。

3 种模型的误差对比如表1 所示。对比表1 数据可知，该文模型与BP 神经网络模型相比，EMAPE下降了1.19%，Emax下降了6.60%；与常规GRU 神经网络模型相比，EMAPE下降了0.79%，Emax下降了2.34%。观察图3 可以看出，Adam-GRU 模型全程的预测精度更好，在负荷波峰和波谷处的误差更小，预测数据更加接近真实值。由此可见该模型的预测精度更高，稳定性更好，具有良好的可行性。

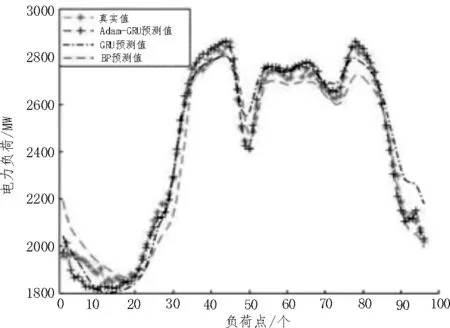
图3 3种模型的负荷预测对比图

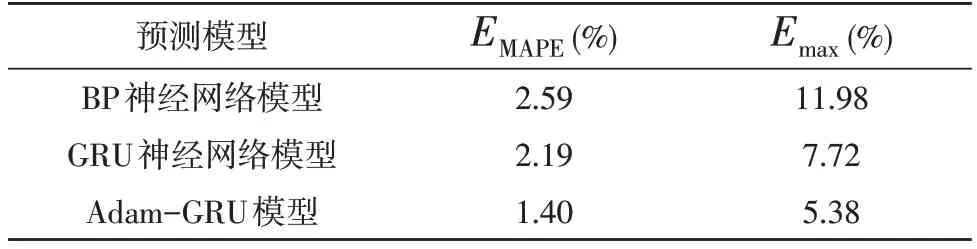
表1 预测结果误差对比

为了进一步验证基于Adam 算法优化GRU 神经网络模型的稳定性，采用传统BP 神经网络模型、常规GRU 神经网络模型和基于Adam 算法优化GRU 神经网络模型分别对该地区电网进行连续一周的负荷预测。预测结果如表2 所示。

表2 连续一周预测结果误差对比

由表2 可以看出，3 种模型的工作日误差均比休息日误差要小。Adam-GRU 模型与GRU 网络模型相比，连续一周预测结果的EMAPE的平均值下降了0.67%，Emax的平均值下降了0.63%。与BP 网络模型相比，连续一周预测结果的EMAPE的平均值下降了1.64%，Emax的平均值下降了2.35%。结果表明，基于Adam 算法优化GRU 神经网络的短期负荷预测模型能够解决常规GRU 神经网络模型中的精度下降问题，有效提高了负荷预测的精度和稳定性。

4 结束语

为了进一步提高负荷预测的精度，该文提出了采用Adam 算法优化GRU 神经网络的短期负荷预测模型，并采用了学习率衰减策略，与随机梯度下降算法相比，Adam 算法可以在训练过程中调整学习率，为不同参数产生自适应的学习率。而且Adam 算法能保证模型在训练过程中每一次更新时，上一次更新的梯度与当前更新的梯度不会相差太大，即梯度平滑、稳定地过渡，可以适应不稳定的目标函数。后续研究工作考虑将GRU 神经网络和其他模型结合，进一步提高预测模型的预测精度。