供热管道部分挖空保温层传热性能分析

庞庆勋，黄昭惠，王添恩

（1.广州珠江电厂，广东 广州511458；2.华南理工大学 电力学院，广东 广州510640）

随着科学水平的进步，人们更加重视对低品位能源的有效利用[1-2]。而目前电厂大多数为热电联产模式[3-4]，兼顾向用户输出电能的同时，通过输送乏汽向用户供热。然而热蒸汽经管道向用户输热的过程中，难免向外漏热，造成热损失，使得经济性降低[5]。很多学者对供热管道的热损失做了研究。王平[6]基于Flow Simulation的方法对直埋供热管道热损失进行了模拟分析，以DN1200直埋预制保温管为例，分析标准保温层厚度的管网在传输过程中的热损失，并通过理论计算对模拟结果进行验证。姜倩等[7]对直埋供热管道泄漏及保温结构破损进行了非开挖检测。刘玉灿等[8]进行了供热管道保温层厚度的动态优化数值模拟研究，提出了使用数值模拟与可视化手段相结合的方法表征供热管道及保温层中温度场的变化，并揭示其规律。

本文对某电厂改造后的供热管道进行了热损失研究，对原保温层进行了部分挖空，挖空区域为封闭空间，里面的介质为空气。因在封闭区域内空气无法流动，利用了空气的低导热性对保温效果进行了强化。在保证挖空区域总空间占比不变的前提下，对比了挖空区域数量为2、4和8以及原保温层结构的温度分布、内外表面温度和热损失。

1 供热管道概况

某电厂机组冷再蒸汽对外供热管道系统现状：每台机组从冷再供辅汽管道逆止门后接出Φ133 mm×6 mm管道，加装手动截止阀、电动截止阀、逆止阀后对外供热。其中1#、3#机组供A公司，2#、4#机组供B公司，两组管道之间再用Φ133 mm×6 mm管道连通并加装手动阀隔离，实现四台机组均能供A公司和B公司。按蒸汽流速30～60 m/s的设计标准要求，机组低负荷（160 MW）时蒸汽压力为1.7 MPa，管道供热能力只有15～20 t/h。由于原供热系统非母管制，当只有单台机组运行或1#、3#机运行、2#、4#机运行时，同时供A公司、B公司、C公司时供热流量受到管径限制。电厂原热用户（A公司、B公司），稳定用汽量约10 t/h，峰值达15 t/h，现在增加了C公司，用热约15 t/h（峰值或达到24 t/h），之后拟增加D公司，用热峰值10 t/h，则总供热流量峰值可达到50 t/h。因此，需要对冷再对外供热管道进行改造。

改造后，供热管道由四条支路管道和一条母管组成，四台冷再机组分别通过四条支路管道向母管输送蒸汽，再由母管向A、B、C、D四家公司输送蒸汽；要求每台机组供热能力达到60 t/h，要求母管供热能力达到120 t/h。管道材质为20#无缝钢管，其中支路管道外径为273 mm，壁厚为8 mm，母管外径为325 mm，壁厚为11 mm。蒸汽管道保温层材料采用复合硅酸铝镁，其中支路管道保温层厚度为120 mm，母管保温层厚度为160 mm。电厂按机组负荷220 MW运行时，供热蒸汽压力约2.4 MPa，温度约305℃。在环境温度为20℃时，管道保温后表面温度不大于45℃。因管道最大热损失最可能出现在接冷再机组的入口段，故对入口段管道进行强化保温研究。

图1（a）为裹有120 mm保温层接冷再机组的入口段的蒸汽管道；图1（b）～（d）为部分挖空保温层的蒸汽管道，挖空厚度为60 mm，保证挖空总截面积不变的前提下，对挖空数为2、4和8的保温层结构进行保温效果的对比研究。

2 数值模型与求解

2.1 物理模型

本文采用有限元仿真软件COMSOLMultiphysics5.5对图1中四种保温结构进行数值模拟。其中计算域包括保温层、管壁和挖空区域中的空气。在空气计算域设置COMSOL材料库中“Air[gas]”材料，保温层和管壁计算域设置空材料，分别输入硅酸铝镁和20#无缝钢管的物性参数。为了简化计算，本文不对管内流动进行数值求解，而是通过计算管槽内强制对流传热关联式，设置第一类和第二类边界条件，数值求解为稳态过程。

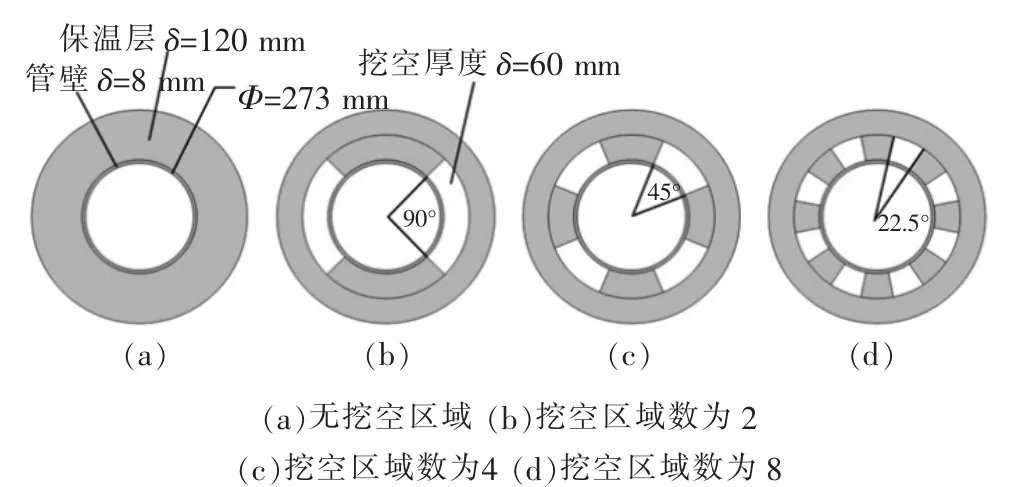
图1 接冷再机组入口段管道保温层（厚度δ=120 mm）截面示意图

2.2 控制方程与边界条件

管壁和保温层的传热遵循能量守恒方程：

式中：T为温度；ρ为密度；τ为时间；U˙为速度矢量；λ为导热系数；cp为比热；ST为内热源。

因为过程为稳态，不涉及流体流动的求解，无内热源，所以时间项、对流项div（ρU˙T）和热源项ST为0。

保温层外表面和管道内表面设置为热通量边界。其中保温层外表面外部温度设置为环境温度25℃；空气自然对流换热系数一般为5～10 W/（m2·K），按保温效果最差的情况进行研究，此处取10 W/（m2·K）。管道内表面外部温度设置为供热蒸汽入口温度；管道内表面对流换热系数按传热学管槽内湍流强制对流传热关联式计算[9]，努塞尔数Nuf为：

式中：Ref和Prf分别为管内蒸汽的雷诺数和普朗特数；当蒸汽被冷却时取n=0.3。

雷诺数Ref的计算如下：

式中：din为管道内径；u为蒸汽流动速度；v为蒸汽运动黏度。

努塞尔数Nuf与管道内壁对流换热系数hin的关系为：

2.3 网格划分与网格独立性分析

在COMSOL启用用户控制网格，对计算域采用自由三角形网格划分，其中因为挖空区域内为空气，属于流体，故对挖空区域设置边界层，边界层数为3，边界层拉伸因子为1.2，厚度调节因子为3，如图2（a）所示。

为保证数值模型的准确性，进行了网格独立性分析，如图2（b）所示。纵坐标为保温层外表面最高温度，横坐标为网格数。可见，导热问题的数值求解在低网格数的情况下也能保持较高的精度。本文选取网格数1 904进行数值计算。

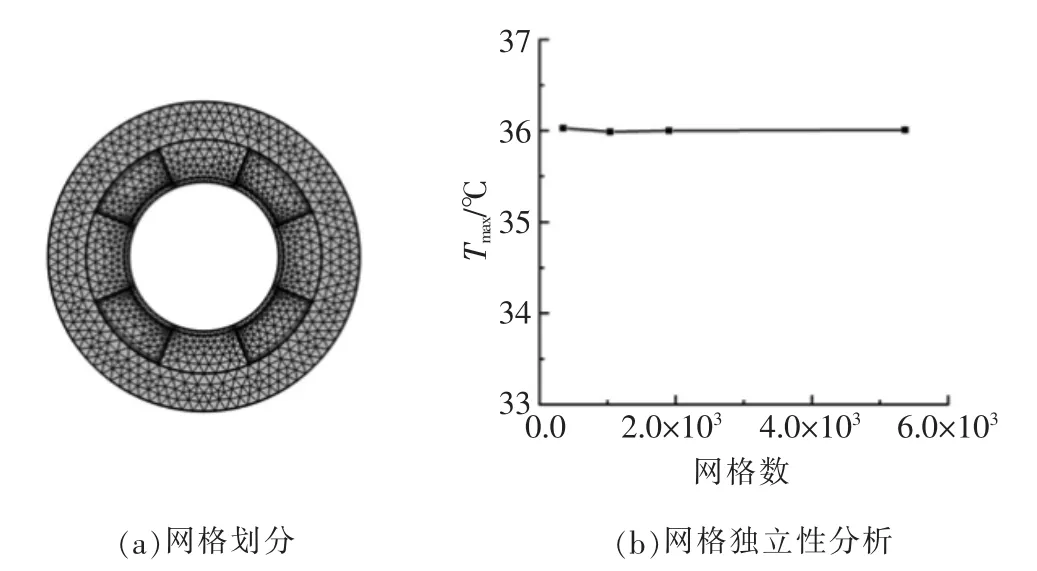
图2 数值模型所采用的网格及其独立性分析图

3 结果与讨论

利用上述建立的数值模型，在保证挖空总截面不变的情况下，探究了挖空区域数量对管道保温层结构温度分布、内外表面温度和热损失的影响。

3.1 保温层挖空区域数对温度分布的影响

分析温度分布对研究强化保温层结构的保温能力有着重要意义。四种不同保温层结构的温度分布如图3所示。

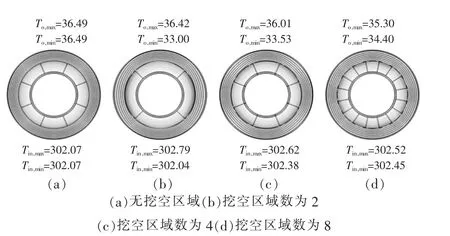
图3 管道保温结构温度分布图（单位：℃）

从图3（a）可以看出，无挖空区域的等温线分布比较均匀，这是因为保温层中不存在挖空区域，均为相同的材质，在每个径向方向上的热阻相等，即每个径向方向上热流量相等，从而温度梯度一致；从图3（b）～（d）可以看出，挖空区域数量越少，温度分布越不均匀。最大温度梯度出现在挖空区域数为2时，见图3（b），保温层结构的挖空区域在图中表现为等温线分布最密集之处。这是因为挖空区域中的介质为空气，且挖空区域为封闭空间，当传热过程稳定后，挖空区域中的传热为空气的导热，空气的导热系数比保温层材料硅酸铝镁低，故挖空区域的热阻更大。根据等效电路的思想，阻力大两端势差大，所以挖空区域的温度梯度更大。对挖空区域数分别为4和8的保温层结构同理，见图3（c）、（d），不同在于后两者挖空区域的温度梯度更小。这是因为挖空区域数越少，挖空区域越大。在对应90°圆心角的扇形区域中，挖空区域数为2的保温层结构空气占比更大，见图3（b），其总热阻更大；而挖空区域数为4和8的保温层结构空气占比递减，见图3（c）、3（d），其总热阻也随之递减。

3.2 保温层挖空区域数对表面温度的影响

图3展示了四种不同管道保温层结构内、外表面温度的最大值和最小值。从图3（a）可以看出，无挖空区域的保温层结构外表面温度均匀，为36.49℃，低于45℃，满足项目改造的要求；从图3（b）～（d）可以看出，挖空区域数为2的保温层结构外表面温差最大，为3.42℃；随着挖空区域数越多，外表面最高温度随之减小，外表面最低温度随之上升，从而外表面温差减小。这也印证了3.1小节中挖空区域数量越少，温度分布越不均匀这一结论。

值得注意的是，挖空区域数为2的保温层结构外表面最高温度比无挖空区域的保温层结构外表面温度更低，这也证明了带有挖空区域的保温层结构效果比无挖空区域保温层结构的效果要好。从图3中还可以看出，无挖空区域保温层结构管道内表面的温度是一致的；而随着挖空区域数的增加，管道内表面的温差减小。但与外表面温差相比，管道内表面的温差很小，可以忽略不计。

3.3 保温层挖空区域数对热损失的影响

使用COMSOL派升值中线积分功能，读取保温层外表面法向总热通量，研究挖空区域数对管道热损失的影响，如图4所示。可以看出，无挖空区域的保温层结构热损失最大，达到了185 W/m。值得注意的是，本文讨论的是二维截面的管道保温层结构，这里的单位长度m是指周向长度，而不是管道轴向长度。挖空区域数为2的保温层结构热损失最小，为157.16 W/m，随着挖空区域数的增大，热损失有轻微的提升，挖空区域数为4和8的保温层结构的热损失分别为157.91 W/m和158.83 W/m。可以看出，影响保温效果的主要因素为挖空区域的空间占比，在保证挖空区域总空间占比不变的前提下，挖空区域的数量对管道热损失的影响可以忽略。

图4 挖空区域数对热损失的影响图

4 结论

本文通过数值模拟的方法对供热蒸汽管道部分挖空保温层结构的保温效果进行了研究。在保证挖空区域总空间占比不变的前提下，对比了挖空区域数量为2、4和8以及无挖空的保温层结构的温度分布、内外表面温度和热损失。结果如下：

（1）挖空区域数量越少，温度分布越不均匀，保温层截面温度梯度随挖空区域数的减小而增大，最大温度梯度出现在挖空区域数为2的保温层结构的挖空区域。

（2）无挖空区域的保温层结构内外表面温度分布均匀，挖空区域数为2的保温层结构外表面温差最大；挖空区域数越多，外表面温差越小。对于不同挖空区域数的保温层结构，管道内表面温差可以忽略不计。

（3）部分挖空的保温层结构的热损失分明显小于无挖空区域的保温层结构；随着挖空区域数的增大，热损失仅有轻微的提升，影响保温效果的主要因素为挖空区域的空间占比。