注重数理思维培养 提升学生核心素养——以带电粒子在圆形磁场中的运动为例

新疆 刘杭州 尚振玉

复杂的物理问题一定是需要在定性的分析和思考后进行定量运算的，而最终能否解决问题，数理思维能力起着关键作用。物理教学中有意识地培养学生的数理思维，对学生科学思维的形成具有重要作用。本文以带电粒子在圆形磁场中的运动为例，探讨学生数理思维的培养。

数理思维是科学思维的重要构成。数理思维是指应用数学思维理解和解决物理问题的思维方式。在高中物理核心素养中，“科学思维”主要包括模型建构、科学推理、科学论证、质疑创新等要素；高中数学核心素养包括“数学抽象”“逻辑推理”“数学建模”“数学运算”“直观想象”“数据分析”。这些素养要求置于高中物理素养要求中一点也不违和，“抽象”“推理”“建模”“运算”“想象”“分析”正是“科学思维”的重要要素。核心素养视域下的数理思维并不只是在应用数学方法解决物理问题，更多的是数学思维和物理思维的相互融合、相互促进。数学和物理自古就是并肩发展的，数学学习和物理学习始终是相辅相成的。数理思维的培养是物理课堂的重要任务，忽视数理思维的培养会造成学生知道问题怎么解决，但是解决不了的尴尬局面。笔者下面以带电粒子在圆形磁场中的运动为例，结合几道例题，探讨学生数理思维的培养。

1.带电粒子在圆形磁场中的运动问题

带电粒子在磁场中的运动特征学生很容易理解，核心思想是洛伦兹力提供向心力，主要方法是“定圆心、画轨迹、找关系”，但关键的是怎样定圆心，从何处找关系。教师在教学中必须引导学生应用数理思维寻求解决办法。

如图1所示，带电粒子在圆形磁场中运动的问题实质是两个相交圆的关系问题，一个是带电粒子运动的轨迹圆，一个是磁场边界圆。相交圆的基本特征为：(1)两圆具有公共弦、两个交点；(2)两圆的圆心连线是公共弦的垂直平分线(两圆关于圆心连线对称)；(3)两圆心与两个交点的连线构成一个四边形(内角和为360°)。教师在教学中引导学生厘清两圆的基本关系是打开思维大门的关键。

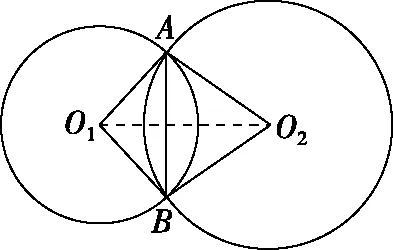
图1

1.1 沿径向入射问题

带电粒子沿径向射入圆形磁场问题有两个重要结论。一个是带电粒子若沿径向射入，则必沿径向射出。教师在教学中如果直接告知学生该结论，则不能让学生形成良好的数理思维。利用两圆关系很容易推导出这个结论，速度实际是沿轨迹圆的切线方向，如图2所示，显然O1A⊥O2A，根据对称性有O1B⊥O2B，从B点射出的粒子速度要与O1B垂直，即粒子出射速度的反向延长线一定过圆心O2。

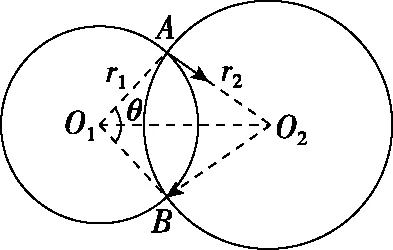
图2

另外一个结论是速度偏转角等于圆弧对应的圆心角。如果教学中只从角度关系证明，只能让学生从数学关系的层面认识到该结论的成立。而从培养学生数理思维的角度，只需让学生认识到速度方向沿轨迹圆的切线，切线和对应半径始终垂直，切线旋转的角度肯定与对应半径旋转的角度相等。

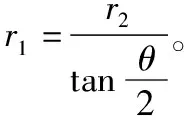
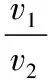
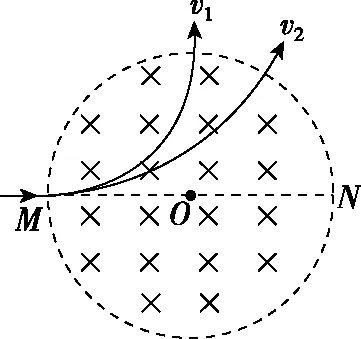
图3

( )

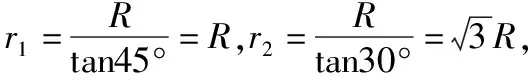
【答案】B

1.2 不沿径向入射问题

不沿径向射入圆形磁场的问题比较复杂，问题设置需附加多个条件，这些条件的引入都是为了辅助寻找角度关系。圆心的确定是该类问题的难点，教师在教学中必须有意识的让学生利用圆的基本性质找到圆心，培养学生的数理思维。常见的不沿径向入射问题有两类：一类是已知入射速度方向、入射点和出射点；另一类是已知速度偏转角和入射点的位置。

类型一：已知入射速度方向、入射点和出射点问题

过入射点做速度方向的垂线与入射点、出射点连线的中垂线交于一点，该点即为圆心。确定圆心，根据已知条件，寻找角度关系即可求解。

【例2】(2016年全国卷Ⅱ第18题)一圆筒处于磁感应强度大小为B的匀强磁场中，磁场方向与筒的轴平行，筒的横截面如图4所示。图中直径MN的两端分别开有小孔，筒绕其中心轴以角速度ω顺时针转动。在该截面内，一带电粒子从小孔M射入筒内，射入时的运动方向与MN成30°角。当筒转过90°时，该粒子恰好从小孔N飞出圆筒，不计重力。若粒子在筒内未与筒壁发生碰撞，则带电粒子的比荷为

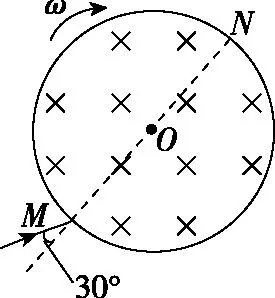
图4

( )

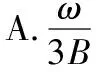
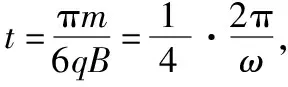
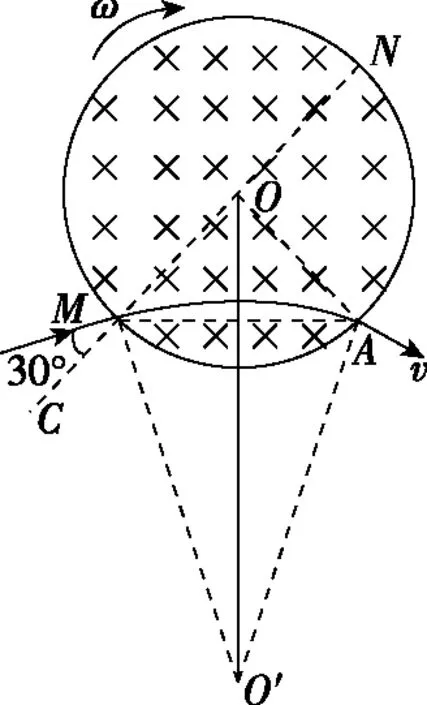
图5

【答案】A

类型二：已知速度偏转角和入射点的位置问题

先做出过入射点速度方向的垂线，然后过边界圆的圆心做速度偏转角的补角的角平分线，二者的交点即为圆心。根据圆的性质，速度是沿轨迹圆的切线方向，两切线的交点一定在相交圆的圆心连线上。

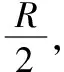
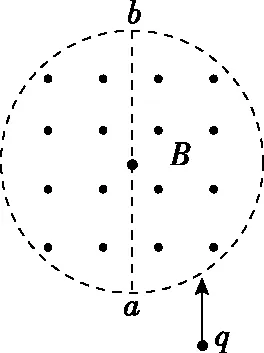
图6

( )

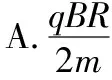
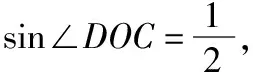
图7

【答案】B

天空变得更亮了，白色云朵多了起来，一大团一大团地簇拥在一起。雪白的云团上有许多黑洞似的暗斑，远远望去，像极了一个个不规则的蜂巢。

综上所述，若教师不在教学过程中引导学生通过数理思维建构正确地确定圆心的方法，学生很难做出轨迹圆，就不能很好地解决上述两类问题，可见培养数理思维的重要性。

1.3 极值问题

极值问题是带电粒子在圆形磁场中运动的重点问题，教学中需要借助旋转圆、放缩圆、平移圆等方法辅助学生分析问题。但从解决问题的角度出发，画出很多轨迹圆并不能真正地帮助学生快速、正确地解决问题。因此，教师应该引导学生从数理思维的角度思考问题，该类问题常设置为粒子运动时间最长或半径最大，解决问题则是依靠圆的唯一性原则，一是圆的最大弦是直径，二是轨迹确定的情况下，圆外一点到圆的切线是唯一的。从这个角度考虑问题可以有效地锻炼学生的数理思维能力。

类型一：弦是直径

若带电粒子在圆形磁场中入射、出射的距离最远，则边界圆的弦(公共弦)一定是轨迹圆的直径，即弦是直径。

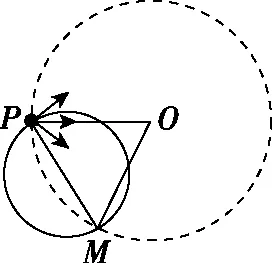
【例4】(2017年全国卷Ⅱ第18题)如图8，虚线所示的圆形区域内存在一垂直于纸面的匀强磁场，P为磁场边界上的一点，大量相同的带电粒子以相同的速率经过P点，在纸面内沿不同方向射入磁场。若粒子射入速率为v1，这些粒子在磁场边界的出射点分布在六分之一圆周上；若粒子射入速率为v2，相应的出射点分布在三分之一圆周上。不计重力及带电粒子之间的相互作用。则v2∶v1为

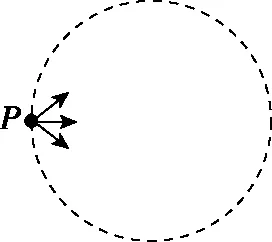
图8

( )

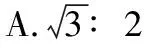
甲

【答案】C

类型二：直径是弦

若粒子在圆形磁场运动的时间最长，则边界圆的直径一定是轨迹圆的弦，即直径是弦。该类型的问题适用于轨迹圆的直径大于边界圆的直径的情况，通过“直径是弦”可以迅速找到出射点，快速解决问题。

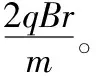
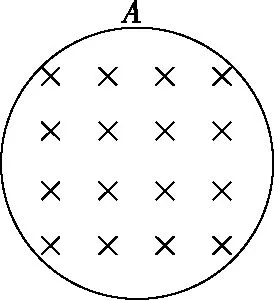
图10

( )

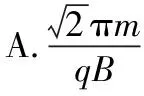
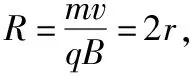
类型三：唯一切线

若圆形是磁场边界的一部分，粒子射出磁场的最大偏转角一定对应边界圆的唯一切线。由于轨迹圆的圆心角等于弦切角的二倍，则圆外一点到边界圆的切线对应的弦切角最大，对应的圆心角也最大。

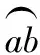
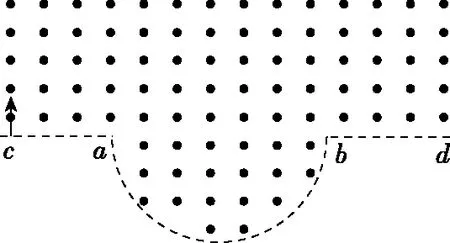
图11

( )

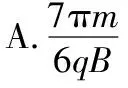
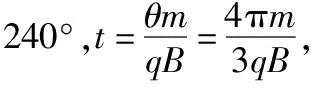
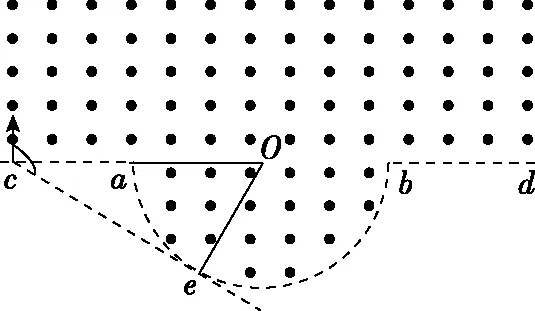
图12

综上所述，教师在教学中注重数理思维的培养，让学生有意识的思考临界条件下两圆关系的唯一性，同时结合旋转圆、放缩圆等方法，让学生形成正确的思维方式。

1.4 磁偏转与磁聚焦

磁偏转和磁聚焦是带电粒子在圆形磁场中运动的特殊问题，当轨迹圆和边界圆的半径相等时，平行入射的等速粒子会汇聚于一点，教学中常借助多媒体辅助描绘轨迹的动态圆进行解释。因为轨迹圆和边界圆的半径相等，故两圆心与两圆交点的连线构成的四边形为菱形，只需任意选取入射位置画出轨迹圆，即可说明磁偏转和磁聚焦的特点，如图13所示。

图13

2.培养数理思维的策略和建议