牵一发动全身
——命题和试题改编的自洽性探讨
江苏 孙鹰渊
在高中物理力学问题中,“滑块—木板”类问题有多种不同角度的分析方法,而多样的解答思路既能培养学生发散思维,又能检验物理问题的自洽程度。“病态”的问题可能会导致不同的解答思路得到不同的结论,出现自相矛盾的情况。本文以一道“病态”的改编题为例,分析其产生矛盾的原因,并对教师命题和试题改编提出建议。
1.一道改编题引发的矛盾
该试题为一道改编题,多次出现在各学校的阶段检测卷上。该题与原题有基本相同的问题情境,仅更改了原题的一个已知数据。但由于该数据的更改,产生了结果的矛盾。
【例题】如图1所示,在平台AD中间有一个长为2l的凹槽BC,质量为m,长度为l的滑板上表面与平台AD等高,质量为2m的铁块(可视为质点)与滑板间的动摩擦因数为μ1,铁块以一定的初速度滑上滑板后,滑板开始向右做匀加速运动,当滑板右端到达凹槽右端C时,铁块与滑板的速度恰好相等,滑板与凹槽右侧边碰撞后立即原速反弹,左端到达凹槽B端时速度恰好为零,而铁块则滑上平台CD。已知重力加速度为g。求:

图1
(1)滑板与凹槽间动摩擦因数μ2。
(2)铁块滑上滑板时的初速度大小v0。
为了方便讨论,不妨设滑板向右滑动时加速度大小为a1,时间为t1,右端到达C时速度大小为v;向左滑动时加速度大小为a2,时间为t2;铁块向左滑动时加速度大小为a3。
1.1 运动学角度分析
滑板向右滑动时,在水平方向上受到铁块对滑板向右的滑动摩擦力以及槽底对滑板向左的滑动摩擦力;向左滑动时,在水平方向上受到槽底对滑板向右的滑动摩擦力,根据牛顿第二定律得
μ12mg-μ23mg=ma1(1)
μ2mg=ma2(2)
又根据滑板向右做初速度为0,加速度大小为a1的匀加速直线运动,最终速度大小为v;向左做初速度为v,加速度大小为a2的匀减速直线运动,最终速度大小为0,据此可得
v2-0=2a1l(3)
0-v2=-2a2l(4)
当铁块向右滑动时,水平方向只受滑板对铁块的滑动摩擦力,根据牛顿第二定律得
μ12mg=2ma3(5)
铁块向右做初速度为v0,加速度大小为a3的匀减速直线运动,最终速度大小为v,得
v=v0-a3t1(6)
又因为滑板向右加速至v所用时间也为t1,所以
v=a1t1(7)
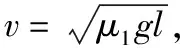
1.2 动能定理角度的分析
滑板向右滑动的过程中铁块对滑板的滑动摩擦力做正功,槽底对滑板的滑动摩擦力做负功,滑板相对于地面位移大小为l,根据动能定理可得
同理,滑板向左滑动的过程中对应的动能定理方程为
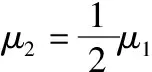
铁块向右滑动的过程中铁块相对于地面位移为2l,所以铁块对应的动能定理方程为
2.矛盾分析
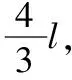
2.1 运动学角度分析
由于凹槽长度为x,板长为l,得
v2-0=2a1(x-l) (11)
0-v2=-2a2(x-l) (12)
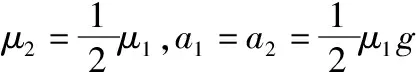
当滑板向右做匀加速直线运动时,可得滑板的运动学方程
同理可得,铁块向右匀减速直线运动的运动学方程
v=v0-μ1gt1(15)
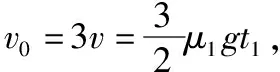
2.2 冲量定理角度分析
由于凹槽长度为x,板长为l,得
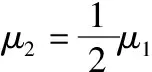
对铁块向右滑动的过程运用冲量定理得
-μ12mgt1=2mv-2mv0(19)
对滑板向左滑动的过程运用冲量定理可得
-μ2mgt1=0-mv(20)
联立可得v0=3v(21)
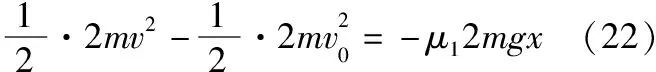
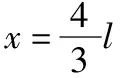
2.3 图像法角度分析
在同一v-t图像中,分别作铁块与滑板速度随时间变化的图像,图像中滑板在t1时刻的位移为l1,铁块位移为l2,v-t图像如图2所示:
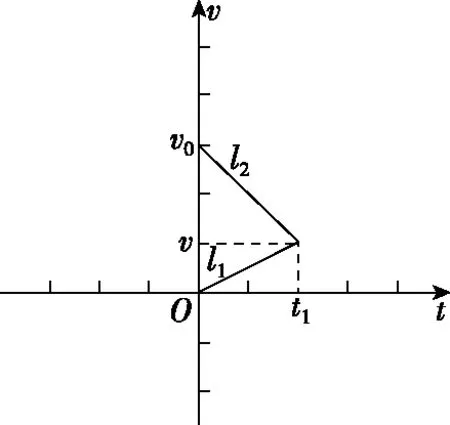
图2 铁块与滑板速度随时间变化图像
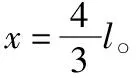
2.4 矛盾产生原因分析
该类改编题的矛盾来源于物理情境和已知条件的不自洽。在例题的情境中,约束条件为铁块恰好与木板速度相等,铁块滑上平台CD,滑板返回最左端时速度恰好为零。在这些约束条件下,凹槽长度与滑板长度应满足4∶3的比例关系。原题在设计时应是为了减少学生的计算量,提供了“过剩”的已知条件,引导学生从运动学或者能量角度进行分析。而改编题未能关注到这个隐含的比例关系,反倒将原本很巧妙的“助推器”改编成了存在错误的“绊脚石”,使得学生在分析求解时出现矛盾。中学生在解题时,一般不会同时从两个角度对问题情境本身的合理性进行图像分析,对问题的认识停留在浅层的求解作答阶段,不能识别问题的错误。此类“病态”问题不利于检测学生对“滑块—木板”模型的掌握情况。
3.命题及试题改编的启示
为避免“病态”问题影响教师对学生知识掌握情况的检测,教师在命题或试题改编时需要谨慎分析,确保物理情境与已知条件自洽。
(1)尝试多角度分析,预设学生的分析方法
教师在命题前需预设学生可能的分析方法,并针对每种分析方法制定有效的评价方式。学生在解决高中物理力学问题时,常从运动学、能量、动量或是冲量的角度进行思考。教师需要在命题时从这四个角度充分分析题设情境,确定每个思考角度对应的关键步骤,从而设置有效的评价方式。若学生未能掌握好某一角度的分析方法,便容易在分析中出现错误,这时教师可以在学生的分析过程中给予对应的提示与帮助,辅导学生巩固该角度的分析方法。同时,教师可以引导学生从其他角度深入分析该问题,通过分析结果的一致性帮助学生掌握多种物理分析方法。
(2)尝试减少已知条件,理清物理量间的内部约束
命题或试题改编时,可以尝试减少已知条件,探究物理量之间隐含的内部约束。当物理情境复杂时,教师较难直接发现物理量之间存在的隐含约束条件,教师需要在命题或是试题改编时通过多角度的计算,尝试寻找物理量之间的潜在联系。若是在命题时,教师发现物理量之间存在的关系较难分析,且与试题考查的知识点关联不大,教师可以将此隐含条件作为已知条件给出,避免学生解题时走歪路;若是在试题改编时,教师通过减少已知条件,发现了物理量之间存在的隐含关系,一定要注意同步变更相关物理量的数据,避免出现矛盾;同时教师也可以设置相关拓展任务,引导学生寻找部分物理量之间的内在联系。
(3)尝试运用模拟软件,检验物理情境的合理性


