透析洛伦兹力冲量的应用
安徽 徐建强 崔北元
叠加场作用下物体的非匀变速直线运动、曲线运动问题以及并列电磁场下的多解问题是学生复习过程中的难点,本文从物理观念的本质出发,通过模型建构推导洛伦兹力冲量表达式,巧妙解答此类问题,深化学生对物理观念的理解。
一、推导洛伦兹力冲量公式
1.构建情境
如图1所示,空间中存在垂直于纸面向里的匀强磁场,磁感应强度为B,一电荷量为q、质量为m的带正电粒子以初速度v0垂直于磁场进入匀强磁场中,仅在洛伦兹力作用下做匀速圆周运动,运动一段时间后速度变为v,把带电粒子的速度和洛伦兹力进行正交分解,分别以vx0、vx为初速度和末速度沿x轴方向的分量,分别以vy0、vy为初速度和末速度沿y轴方向的分量,任意时刻带电粒子所受洛伦兹力F在x轴和y轴方向的分量分别为Fx、Fy。
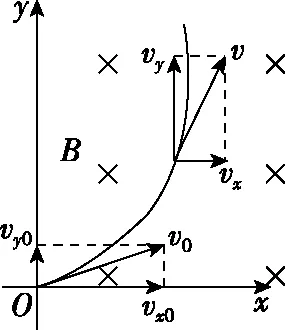
图1
2.微元积累法推导
分析粒子在x轴方向的运动,取很小一段时间Δt内x轴方向的速度变化量为Δvx;由左手定则可知x轴方向的洛伦兹力仅由y轴方向的速度分量vy决定,其大小为Fx=qvyB。
由动量定理有-qvyBΔt=mΔvx(负号表示洛伦兹力与vx0方向相反),其中vyΔt=Δy
两边求和有-qB∑vyΔt=m∑Δvx,其中∑vyΔt=y,∑Δvx=vx-vx0
得qBy=mvx-mvx0
同理可得qBx=mvy-mvy0
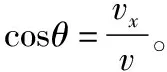
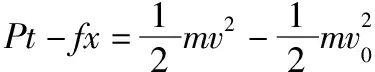
二、典例剖析
1.并列场作用下运动问题
【例1】现代科学仪器常利用电场、磁场控制带电粒子的运动。在真空中存在着如图2所示的多层紧密相邻的匀强电场和匀强磁场,电场和磁场的宽度均为d。电场强度为E,方向水平向右;磁感应强度为B,方向垂直纸面向里。电场、磁场的边界互相平行,一个质量为m、电荷量为q(q>0)的粒子在第1层电场左侧边界某处由静止释放,粒子始终在电场、磁场中运动,不计粒子重力及运动时的电磁辐射。
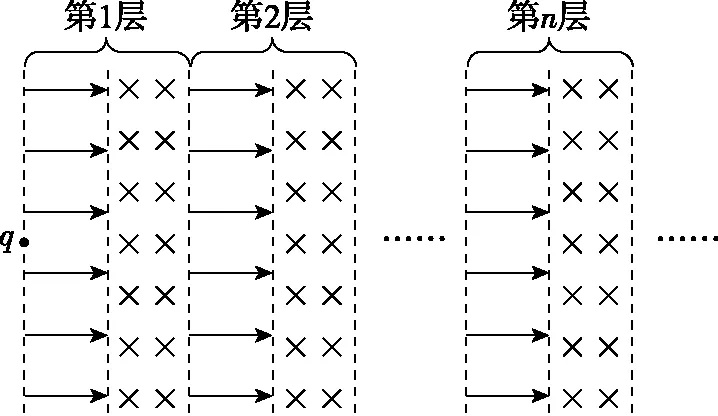
图2
(1)求粒子在第2层磁场中运动时速度v2的大小与轨迹半径r2。
(2)粒子从第n层磁场右侧边界穿出时,速度的方向与水平方向的夹角为θn,试求sinθn。
(3)若粒子恰好不能从第n层磁场右侧边界穿出,试问在其他条件不变的情况下,也进入第n层磁场,但比荷较该粒子大的粒子能否穿出该层磁场右侧边界,请简要推理说明。
【分析】(1)粒子在第2层进入磁场时已经经历两次电场加速,由动能定理可求得进入第2层时的速度,再由洛伦兹力提供向心力即可求得轨迹半径;(2)粒子在整个运动过程中,水平方向的电场力改变速度的大小,竖直方向仅受因为水平分速度产生的洛伦兹力,该力引起竖直方向速度的变化,故可以利用洛伦兹力冲量公式找到竖直分速度,利用电场力做功求出末速度,从而解答该问。(3)粒子不能从第n层磁场右侧边界穿出即粒子到达右侧边界时速度恰好竖直向上,仍可利用洛伦兹力的冲量公式求出宽度d与粒子比荷的关系进而求解。
【解析】(1)粒子在进入第2层磁场时,经过两次加速,中间穿过磁场时洛伦兹力不做功
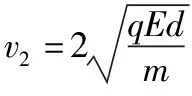
粒子在第2层磁场中受到的洛伦兹力提供向心力
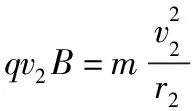
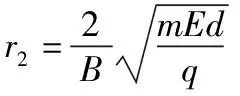
(2)设带电粒子从第n层磁场右边界穿出时速度为vn,竖直方向分速度为vny,如图3所示,带电粒子在竖直方向只受洛伦兹力,洛伦兹力在竖直方向上的冲量与粒子在磁场中水平方向的位移nd成正比,由动量定理得
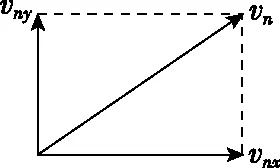
图3
qBnd=mvny-0
带电粒子运动过程中只有电场力做功,由动能定理得
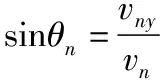
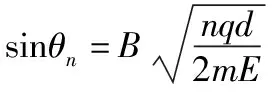
(3)若粒子恰好不能从第n层磁场右侧边界穿出,则粒子到第n层磁场右侧时速度方向恰好竖直向上,设其速度为vn0,分别从开始到第n层磁场右侧由动能定理和竖直方向上的动量定理得
qBnd=mvn0-0
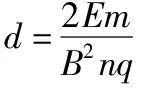
【点评】本题考查带电粒子在组合场中的运动,在处理后两问时很容易想到借鉴第(1)问的处理思想,根据电场力做功明确末速度,再根据洛伦兹力充当向心力找出第n层磁场中的半径关系,由等差数列规律得出通项式,即可求出sinθn,这是传统参考答案给出的复杂解法(在此不再赘述),这种解法要求学生能正确分析物理过程,并能灵活应用数学知识,难度较大,对学生综合素养要求极高。但采用的洛伦兹力冲量法大大简化了解题过程,免去了分析运动细节找圆心、半径及几何关系等困难,起到高效解题的效果,针对这类并列场问题此法值得推荐给考生学习。
2.叠加场作用下滚轮线问题
【例2】如图4所示,空间存在范围足够大的垂直于xOy平面向外的匀强磁场和沿y轴正方向的匀强电场,磁感应强度大小为B,电场强度大小为E。让质量为m,电荷量为q(q>0)的粒子从O点以初速度v0沿y轴正方向发射。研究表明,粒子在xOy平面内做周期性运动,且在任一时刻,粒子速度的x分量vx与其所在位置的y坐标成正比,比例系数与电场强度E大小无关。不计重力和粒子间的影响,求:
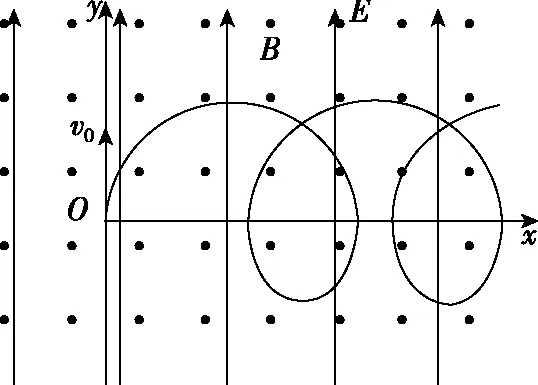
图4
(1)该粒子运动过程中速度的最大值vm;
(2)当粒子运动速度达到最大时,粒子距x轴的距离。
【分析】电场力改变速度大小,洛伦兹力改变速度方向,当速度最大时即电场力做功最多,结合洛伦兹力的作用可知此时速度方向水平,在整个运动过程中粒子水平方向只受因竖直方向分速度产生的洛伦兹力影响,故可列出该粒子在水平方向上的动量定理表达式进行求解。
【解析】粒子运动到最高点,其速度最大并且方向沿x轴,对粒子由x轴方向的动量定理有
qBy=mvm-0
从O点到最高点只有电场力做功,由动能定理有
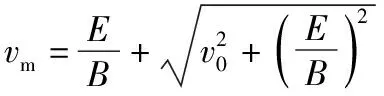
【点评】(1)该解法从洛伦兹力和电场力的作用特点出发,利用动量定理、动能定理进行求解,有效避免出现题干中理解vx与其所在位置的y坐标成正比,比例系数与电场强度E大小无关的思维难度。教学中还可以改编问题,若已知粒子第一次速度达到最大所用的时间,则还可以利用水平方向动量定理求解水平方向位移,从而提升学生思维能力。
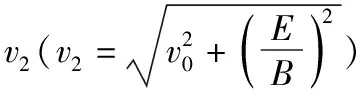
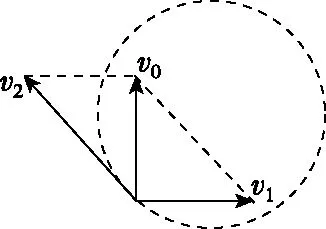
图5
3.拓展应用——磁约束下非匀变速直线运动问题
【例3】如图6所示,空间有一个范围足够大的匀强磁场,磁感应强度为B,将一个质量为m、电荷量为+q的带电小圆环套在一根固定的绝缘竖直细杆上,杆足够长,环与杆之间的动摩擦因数为μ。现使圆环以初速度v0向上运动,经时间t圆环回到出发位置。不计空气阻力。已知重力加速度为g。求当圆环回到出发位置时速度v的大小。
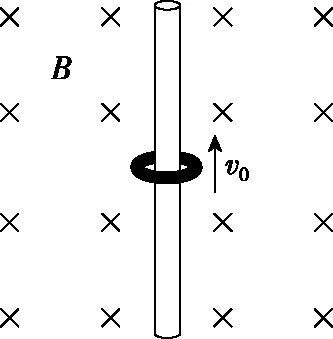
图6
【分析】圆环在沿杆运动过程中对其受力分析可知,上升阶段速度减小导致洛伦兹力减小,而所受摩擦力与洛伦兹力成正比,故为非匀变速直线运动,下降亦是如此。由于已知运动总时间,则可以尝试利用动量定理求解速度,不难发现摩擦力的冲量为μqBy,y为竖直方向的位移,全程位移为零从而有效消除摩擦力的冲量,进而解答题目。
【解析】在圆环运动的过程中,圆环受向下的重力mg、水平方向的洛伦兹力qvB、细杆的弹力FN和摩擦力f,其中f一直与运动方向相反,且摩擦力的大小f=μFN=μqvB。
圆环从开始向上运动到回到出发位置的过程中,取竖直向上为正方向,根据动量定理有
If-mgt=-mv-mv0
而If=-∑μqv上BΔt上+∑μqv下BΔt下=μqB(x下-x上)=0
解得v=gt-v0


