不同转向架构型对高速列车列车风及非定常尾迹的影响

郭 婷，夏 超，*，储世俊，杨志刚，3

(1. 同济大学 汽车学院，上海 201804；2. 同济大学 上海地面交通工具风洞中心，上海 201804；3. 北京民用飞机技术研究中心，北京 102211)

0 引 言

列车是贴地高速运行、外形细长的运动物体，气流沿列车表面的发展会受到转向架区域、车厢间隙以及地面效应等影响[1]，使得列车底部和尾部流场非线性发展，呈现出复杂的三维非定常特性，包含剪切层、涡脱落、分离泡以及反旋流向涡对等多尺度流动结构的相互耦合。随着高速列车速度的不断提升，列车尾部非定常尾迹引起的列车风安全问题越来越凸显[1-3]。列车风是指列车高速运行时诱导周围气流运动，形成沿列车逐渐增厚的边界层以及具有复杂三维湍流特性的尾迹流动，而过高的列车风速度会使站台的乘客、设备和轨道旁人员失稳甚至被卷入尾迹中，造成人员伤亡或列车受损[3-5]。为了降低列车风峰值，保证列车运行时的安全性，就必须在充分了解列车尾迹结构的基础上理解其与列车风之间的关系，以提供更加准确的列车风评估手段和控制方法。

之前的研究已经得到典型的列车风分布[4-5]，并发现列车风的峰值主要出现在近尾迹区域，且呈现强烈的间歇性特征[5-7]。目前学者普遍认为该峰值是由列车尾涡的非定常特性引起的[7-9]。近年来，关于列车尾迹的研究，学者们做了大量的探索。2016年，Bell等[9]通过缩比风洞实验的方法，采用多孔探头对ICE3两节编组列车的尾迹进行了测量，研究指出高速列车的时均尾涡以一对反旋的对称流向涡对为主导，且呈现出正弦式的展向不对称周期性振荡。2018年，Xia等[10]进行风洞缩比试验，采用粒子图像测速和本征正交分解（POD）相结合的方法剖析了尾涡动力学演化特性，提出CRH3列车的三维瞬时尾涡是以交替脱落的半环形流向涡对为主导。

以往的研究还表明底部转向架结构引起的底部流场扰动对尾流的非定常特性有很大的影响[11-13]。2018年，Wang等[11]基于ICE3列车模型，数值模拟研究了转向架对高速列车列车风速度的影响，发现转向架的存在可以显著改变气动载荷的预测，增加列车风速度，特别是在轨道侧位置。同时指出转向架并不是引起尾迹展向振荡的直接原因，认为展向运动可能是由于流向涡对的自然对流不稳定性引起的。2019年，Dong等[12]通过对四种不同简化转向架结构流场的数值模拟比较，论证了过于简化转向架（只有转向架舱，无转向架结构）会导致过高估计车体下流速，同时会增加底部的湍流度。2019年，Liu等[13]利用数值模拟和动力学模态分解（DMD）相结合，研究转向架对非定常尾迹的影响，研究表明对于无转向架模型，尾涡的产生有两个固有的来源，即排障器和尾车车头；而对于有转向架模型，尾涡主要是由尾车的排障器产生的。

如上所述，高速列车尾迹呈现出复杂的三维湍流特性，尾涡的动力学演化特性尚不明确，同时其与近尾迹列车风峰值的相关性还未被完全建立，此外转向架对尾涡的产生和演化的影响仍未达成共识。

近年来，为理解复杂的湍流结构和相关机理，学者结合各种数据驱动算法发展了多种非定常流场的模态分解方法[14-18]。通过模态分解方法得到的降阶模型可以直观的展现非定常流动随时间和空间的演化规律，因此对于湍流尾迹的非定常流动机理分析具有重要意义。目前应用广泛的是POD和DMD[14-15]。其本质都是寻找一组低维的子空间（流动模态或相干结构），将高维、复杂非定常流场表示为这些子空间在低维坐标系上的叠加，从而在低维空间中描述流场随时间和空间的演化规律[16]。然而，当流动的相干结构出现在低能量或多频率时，传统的POD并不能得到很好的结果[17]。2016年，Sieber等[17]提出Spectral POD方法，通过对相关矩阵沿对角线应用低通滤波器来增加矩阵的对角线相似度，既而增强底层信号动力学的相似度。相较于POD，SPOD更有利于分离发生在多个频率和能量的流动现象。自从该SPOD方法被提出，它已经成功应用于多种基础湍流流场的分析[17,19-21]，如Chu等[19]将SPOD应用于圆柱和海豹胡须柱的尾涡动力学演化分析中，发现了海豹胡须柱尾迹中存在着四种典型的涡脱落模式，并阐明了其可以有效抑制卡门涡脱落的机制。然而，SPOD方法在更复杂三维湍流尾迹流场，如高速列车三维尾迹中的应用还鲜有涉及。

因此本文采用增强型延迟分离涡数值模拟方法（IDDES）和SPOD方法相结合，研究三种不同转向架构型对高速列车列车风和非定常尾涡动力学特性的影响。

1 方 法

1.1 高速列车模型

本文的研究对象为1/50缩比两节编组的CRH3高速列车模型，尺寸为15.7W×1.0W×1.1W（长L×宽W×高H），W= 0.065 m，包含2个排障器，4个转向架。三种不同转向架构型分别为：不对称转向架（Asymmetric Bogies，AB）、对 称 转 向 架（Symmetric Bogies，SB）和无转向架（Without Bogie，WoB；带有转向架空腔）。高速列车模型的三维图如图1所示，三种转向架构型如图2所示。不对称转向架和对称转向架分别对应动车和拖车转向架结构，车轮、轮轴及轮对支撑框架均相同，其中车轮的直径为d= 20 mm，宽度为2.6 mm，其他相关尺寸如图2所示（单位为mm）。

图1 1/50两节编组CRH3高速列车模型Fig. 1 1/50 scaled high-speed train model CRH3 with two cars

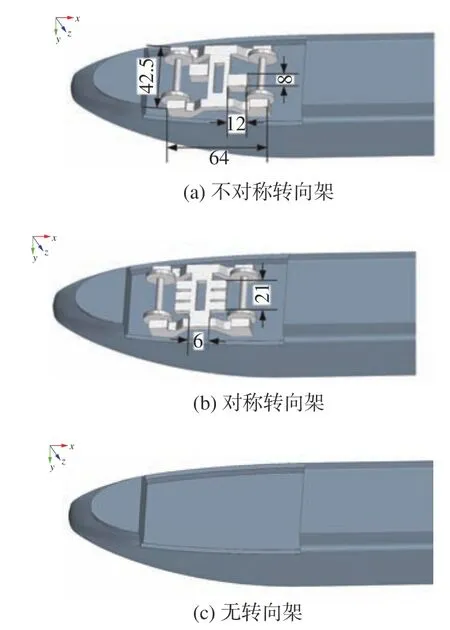
图2 三种不同转向架构型Fig. 2 Bogie configurations：(a) asymmetric bogies (AB)；(b)symmetric bogies (SB)；(c) without bogies (WoB)

1.2 计算设置

本文采用了基于k-ω SST的 IDDES混合方法进行数值模拟。IDDES混合方法结合了延迟分离涡模拟（DDES）和壁面模化大涡模拟（WMLES）的能力，可以在不同的流动区域激活RANS和LES，为高雷诺数下的复杂湍流流动研究提供了一种强大的数值方法，可以在一定程度上更好地实现计算资源和计算精度的平衡[22]。因此，选用IDDES方法来计算高速列车周围的复杂流场。计算域如图3所示，尺寸为54W（长）×5.2W（宽）×5W（高），速度入口与列车头鼻部的距离为6.0W，出口与列车尾鼻部的距离为32W，模型阻塞比为2.3%。边界条件指定如下：入口为速度入口（U∞=30 m/s），出口为压力出口，地面为移动壁面边界，车体为无滑移壁面边界，其他边界为对称边界条件。雷诺数为1.3×105（基于U∞和H）。表1给出了计算网格的分布信息，其中Δs表示单元网格在y轴方向的长度，Δl表示单元网格在x轴方向的长度，u∗表示摩擦速度。图4给出了不对称转向架模型中截面、水平截面以及转向架处的网格分布的图片，加密区主要设置在车底、转向架、尾迹区等部分。关于网格无关性验证部分请参见之前的研究[23]。

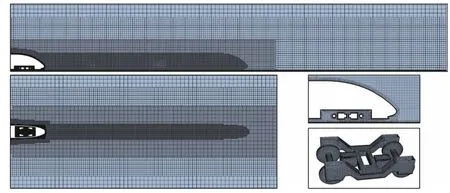
图4 高速列车模型网格分布Fig. 4 Grid distribution around a high-speed train model

表1 网格信息Table 1 Grids information

图3 计算域和边界条件Fig. 3 Computational domain and boundary conditions

1.3 数值验证

为了验证数值模拟计算的准确性，将不对称转向架模型在静止地面边界条件下的计算结果与风洞试验结果进行了对比。该风洞试验的模型以及地面条件均与数值模型一致，有关实验的其他细节可参考之前的研究[10]。图5展示了中截线上列车上下表面时均压力系数分布的试验和数值结果。压力系数的定义如公式（1）所示：

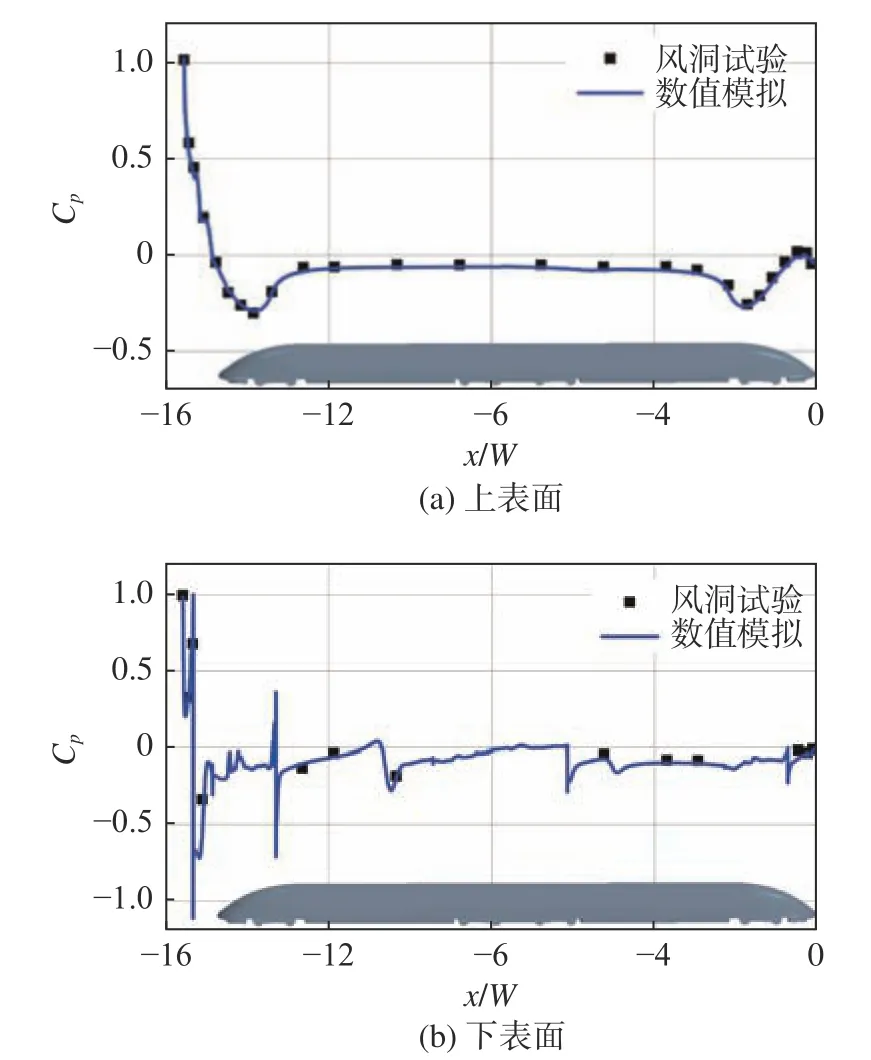
图5 风洞试验与数值模拟中截线上时均压力系数对比Fig. 5 Comparison of time-averaged pressure coefficients along the longitudinal centreline between IDDES and experiment

式中，p为时均表面压力，p∞为 来流静压，ρ为流体密度，U∞为来流速度。

如图5所示，对于上表面和下表面，除了尾部的个别测点外，数值模拟和风洞试验的结果均吻合较好，此外气动力和尾迹速度场的验证结果也较合理，这里因为篇幅限制不再展示，可以参考之前的研究[23]。

1.4 SPOD方法

SPOD方法是在POD方法的基础上增加了额外的时间约束，能够分离发生在多个频率的能量和流动现象，通过改变滤波长度Nf实现从POD到纯粹的DFT（傅立叶分解）连续变换。下面描述算法的关键步骤：

SPOD将速度矢量u（空间位置与时间的函数）分解为时间尺度上的平均速度(x) 和 脉动速度u′(x,t)，脉动速度又分解为空间模态 φi(x) 和时间系数ai(t)的乘积总和：

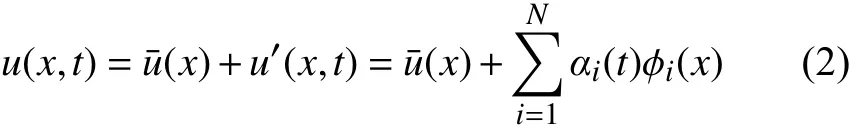
相关矩阵R为：

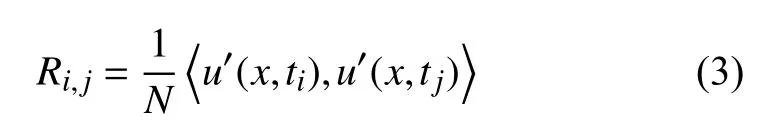
其中 〈,〉表示内积，相关矩阵的维度为N×N。

与传统的POD算法不同，SPOD沿着对角线应用一个简单的低通滤波器来增加矩阵R的对角线相似度，过滤后的相关矩阵S为：

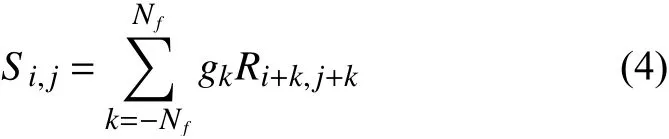
其中g为 滤波器矢量，其长度为 2Nf+1。

后面的步骤和传统的POD相同，

式中：ai为 时间系数， λi为模态能量。时间系数与模态能量成比例，它们仍然是正交的，与单个模态的能量成比例：

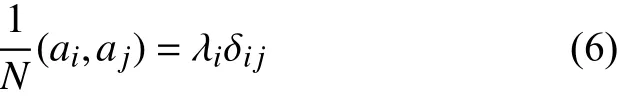
式中，(,)代表向量积， δij为Kronecker符号。

空间模态由速度快照投影到时间系数上得到：

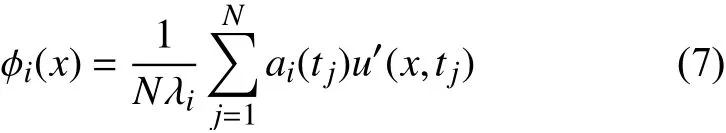
2 结果与讨论

2.1 列车风速度

在数值仿真中，由于列车采用静止处理，因此得到的瞬时速度是以列车为参考系，通常先经过来流速度归一化处理后转换成以地面为参考系的速度，列车风速度的定义如下：

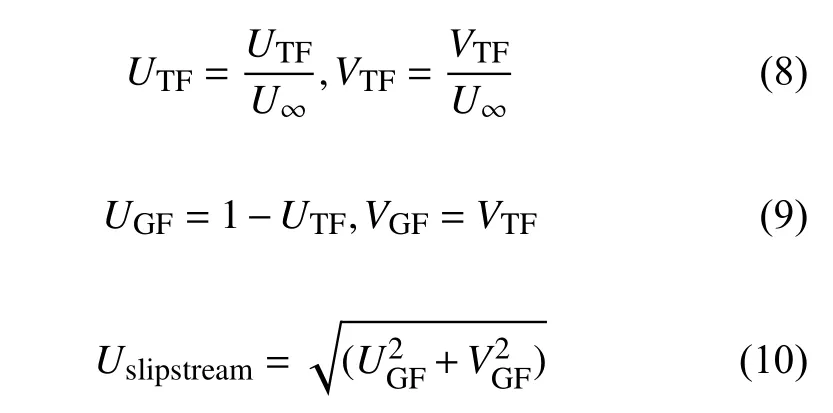
其中，TF表示列车参考系，GF表示地面参考系；U为流体x方向的速度，V为流体y方向的速度。

图6展示了三种转向架结构列车模型在TSI[3]要求的两个监控位置处（轨侧位置(y= 1.0W,z= 0.12W)和站台位置(y= 1.0W,z= 0.50W)）沿x轴方向的时均列车风速度Uh∗和均方根UR∗MS分布。从图6（a、b）可见，转向架结构对轨侧位置的时均列车风速度的影响大于站台位置的影响。在轨侧位置，无转向架的列车风速度峰值最大，达到0.18，出现在近尾迹区x≈6.6W位置处；在同一位置，不对称转向架的列车风速度达到峰值0.14。对于对称转向架，列车风速度分布与不对称转向架相似，但其峰值位置明显滞后于无转向架和不对称转向架，出现在x≈ 10.6W处。此外，在第一个转向架空腔后（x≈−13.5W），无转向架的列车风速度开始高于不对称转向架和对称转向架，且在第四个转向架空腔后，其增长速度逐渐高于不对称转向架和对称转向架。

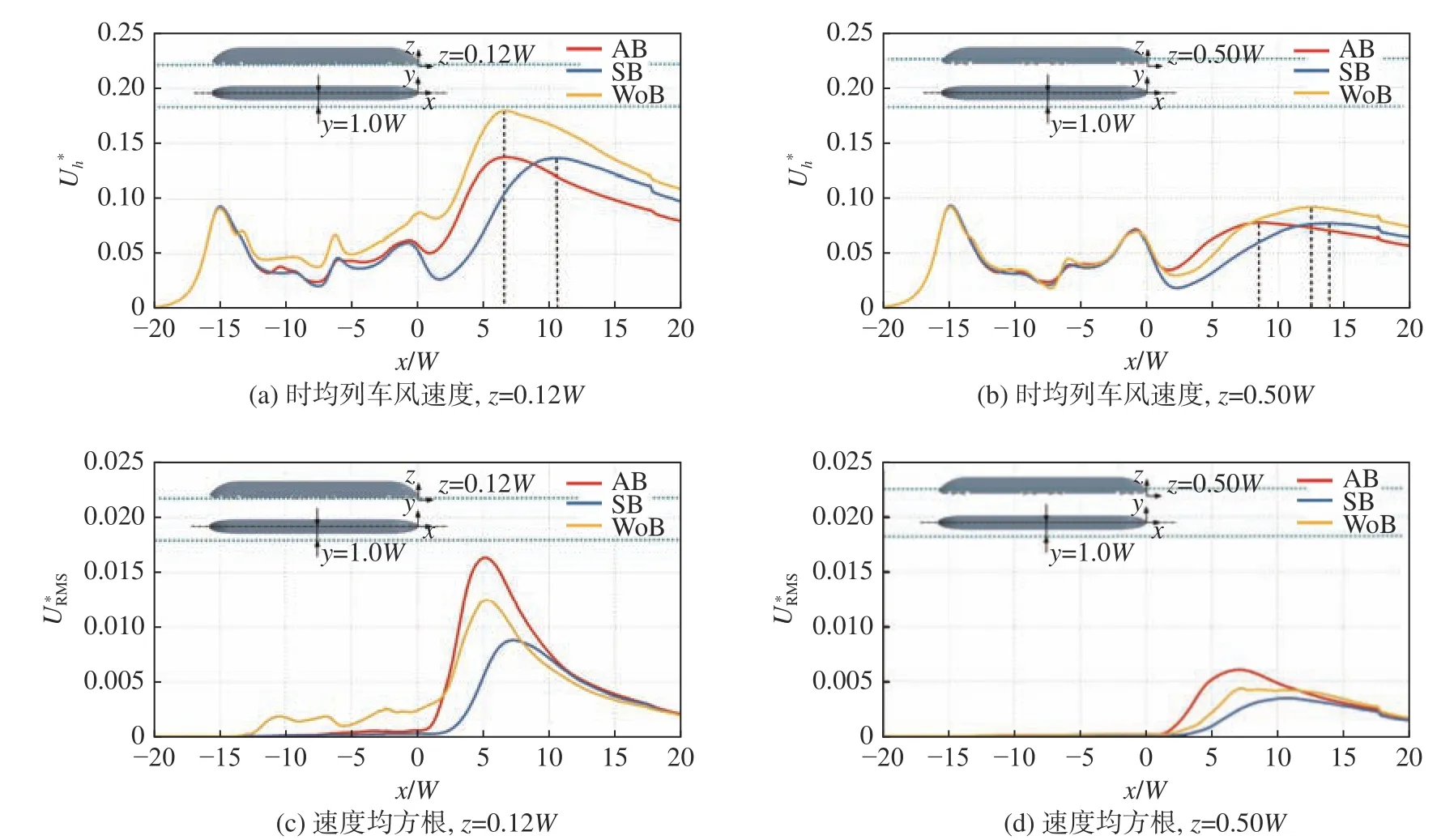
图6 三种转向架结构沿x轴方向的列车风速度分布(y = 1.0W)Fig. 6 Slipstream velocity distributions for three bogie configurations along x direction at y = 1.0W

与时均列车风速度不同，图6（c、d）显示不对称转向架的列车风速度的均方根峰值最大，对称转向架的列车风速度的均方根峰值最小。

2.2 转向架腔内的流场结构

图7展示了三种转向架构型的第一个转向架腔内的瞬时流场拓扑结构。可见不对称转向架的分离涡结构较为丰富且不对称。对于无转向架结构，空腔内的涡结构尺度更大且转向架空腔及其后缘流动分离产生大尺度的流向涡脱落，导致了第一个转向架空腔后（x≈ −13.5W）相对较高的列车风速度，如图6（a）所示。

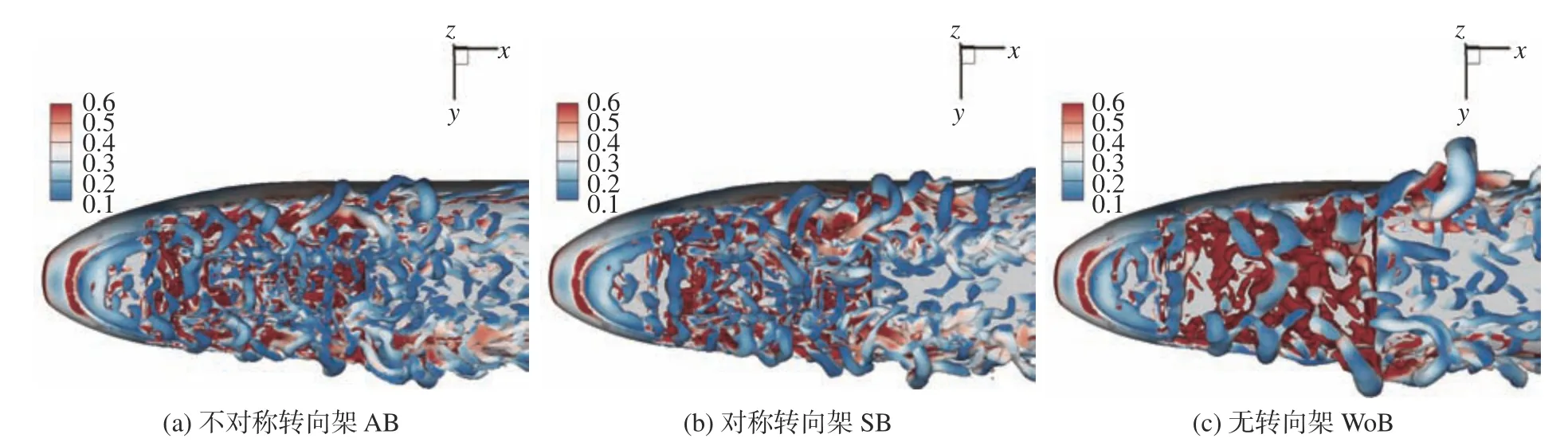
图7 转向架腔内的瞬时流场结构Fig. 7 Instantaneous flow structures in the bogie cavity

2.3 尾迹流场

图8展示了Q准则中Q= 1000时的三种转向架构型的时均尾迹流场。由图可知，三种转向架的尾迹均是由一对反向旋转的流向涡主导；其中，无转向架和不对称转向架的涡结构强度更大，尾车底部两侧的涡脱落结构更加明显。

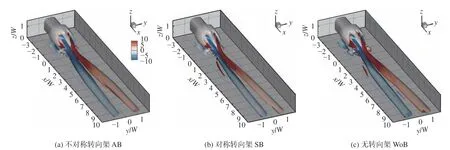
图8 时均尾迹结构(Q = 1 000)Fig. 8 Time-averaged wake flow structures (Q = 1 000)

图9展示了尾迹瞬态压力p= −3.5 Pa表示的三种转向架构型的瞬时流场拓扑结构。可以观察到，对于三种转向架构型，尾迹中的主导结构均是大尺度的半环形流向交替涡脱落，涡腿紧贴地面。三种转向架构型在瞬时尾迹拓扑结构上的主要区别在于尾迹的展向宽度和涡脱落左右交替或同步出现的程度。与对称转向架相比，无转向架和不对称转向架的尾迹展向宽度更宽，当流向涡脱落更大概率地经过轨道侧和站台侧的测点位置时，就会引起较大的列车风速度。对于不对称转向架，如图9（a）所示，由于不对称转向架构型带来的底部扰动与流向涡对的相互作用，使得半环形流向涡交替脱落程度更强。

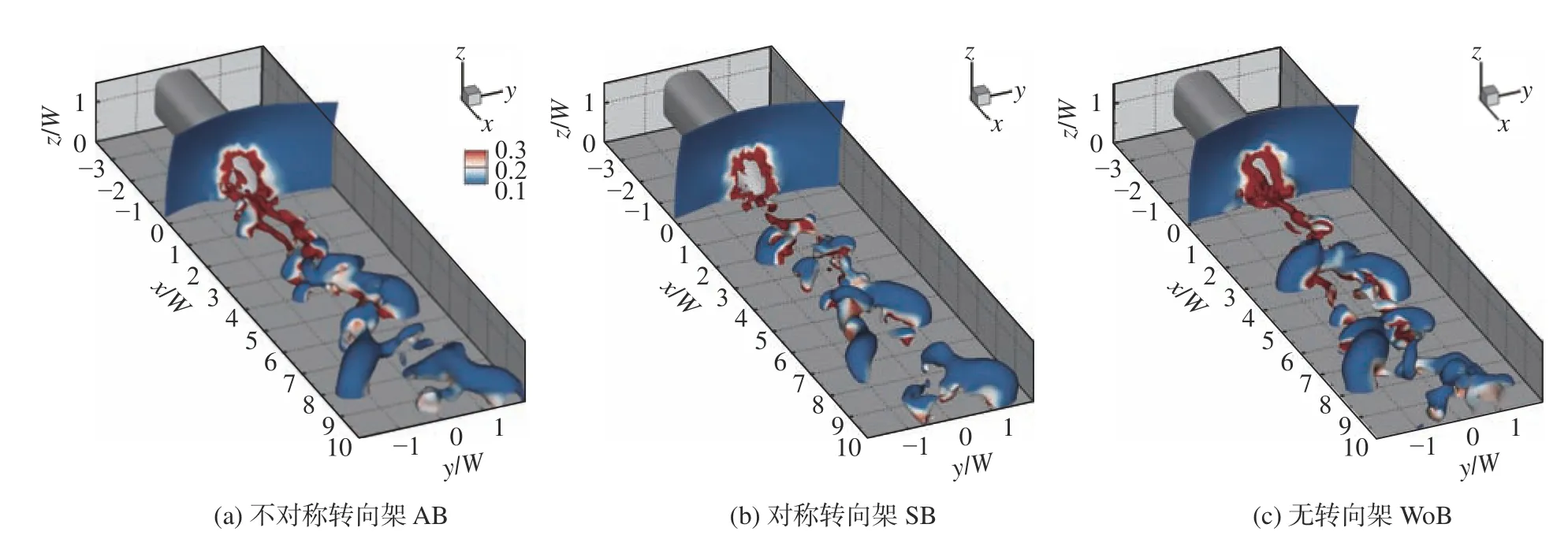
图9 瞬时尾迹结构(p = −3.5 Pa)Fig. 9 Instantaneous wake flow structures (p = −3.5 Pa)

2.4 SPOD结果

2.4.1Nf值的选取

SPOD方法一个重要的参数就是滤波器的大小即Nf的取值，当Nf=0时，SPOD方法转化为POD方法。本文采用SPOD方法对水平面z= 0.12W的尾迹速度场进行处理，首先以不对称转向架为例，介绍了SPOD处理过程中Nf值的选取，随后展示了三种转向架构型的SPOD处理结果。

首先选取Nf= 0、25、40和100，对不对称转向架进行SPOD处理，得到四种取值下的第一对模态（前两个模态Mode1_1和Mode1_2）系数（a1_1和a1_2）的功率谱密度图以及第一对模态两个模态之间的相图如图10所示。从图10（a），即模态系数功率谱结果可见，前两个模态是成对出现的，且SPOD的处理结果比POD（Nf=0）的处理结果模态配对情况更好，峰值频率更明显。同时，结果表明不对称转向架第一阶模态的主要特征频率为St=0.18。图10（b）为对应Nf值下模态系数的相图，当第一对模态系数的相图呈现圆形时，表明第一对模态两个模态之间仅相差90°相位差。对比不同Nf取值结果可知：随着Nf取值的增大，第一对模态的相图逐渐有序，趋于圆形，表明第一对模态配对性逐渐增强，与功率谱密度的结果一致。

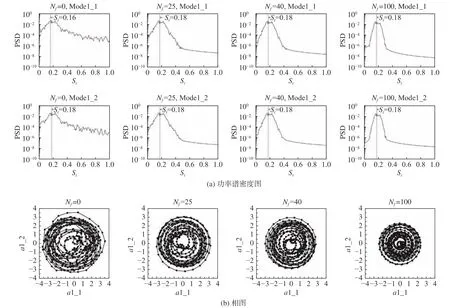
图10 不同 N f取值下不对称转向架第一对模态系数图Fig. 10 Coefficients of the first pair of modes for AB under different N f values

先前的研究[17,19]表明Nf取1～2倍主导模态的周期时得到的结果较好。由公式（11、12）计算可得第一阶模态的周期T约为24。故为得到更好的结果，优先考虑Nf在24～48之间取值。

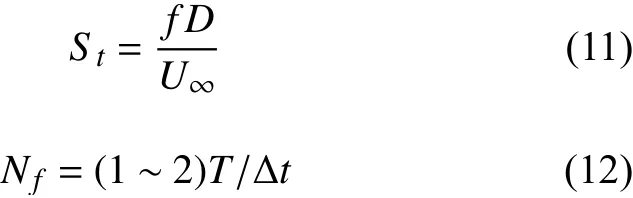
式中：f为频率；D为特征长度，此处为列车宽度此处为列车宽度W= 0.065 m；U∞为 来流速度； Δt为采样时间间隔，此处为0.0005 s。

图11展示了不对称转向架前50个模态的能量占比情况，随着Nf值的增大，第一对模态的能量占比越来越低；而第二对模态的能量占比则随着Nf的增大，先增大后减少。为了使采用降阶模型后的流场重构更接近于原始流场，低阶模态能量占比应该越高越好。因此，综合模态系数与能量占比的结果，当Nf=40时，模态配对良好，特征频率较凸显，同时低阶模态的能量占比较高，故后续采用Nf=40的结果进行分析。

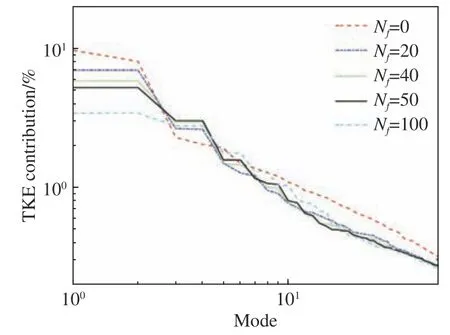
图11 不对称转向架前50个模态能量占比Fig. 11 Energy fraction of the first 50 modes for the AB configuration

2.4.2 SPOD模态及重构结果

以不对称转向架为例，图12展示了流场速度U（流向速度，即x方向速度）和速度V（展向速度，即y方向速度）分别用POD（Nf=0 ） 和SPOD（Nf=40）处理的前两对模态图（由于模态是成对出现，故只展示一对模态中的一个，即mode1_1和mode2_1，其中第一个数字表示模态对的顺序，第二个数字表示同一对模态中的第1或第2个模态）。可以看到两种处理方法所得到的对应的模态结构一致。第一对速度U的模态均呈现出左右不对称分布，速度V的模态则均呈现出左右对称分布，沿着流向位置速度U和V模态都是正负速度交替出现，这与圆柱涡脱落的模态特征相一致。但相较于POD，SPOD处理得到的模态空间结构更为清晰完整，次要结构减小，干扰较小，且识别的模态时间相关性更强（见图10（b）所示）。如POD处理得到的速度U和速度V的第二对模态在近尾迹区较为混乱，表明在近尾迹流场结构比较复杂的情况下，POD提取主要模态的能力不强，可能出现偏差。而SPOD通过在相关矩阵进行对角的低通滤波，处理的结果更为有序，近尾迹区与中尾迹区衔接良好，即SPOD通过模态的时间相关性在众多复杂结构中提取主要模态的能力更强。因此，考虑到高速列车尾迹的复杂及其非定常特性，SPOD方法更适合于高速列车尾迹的分析。

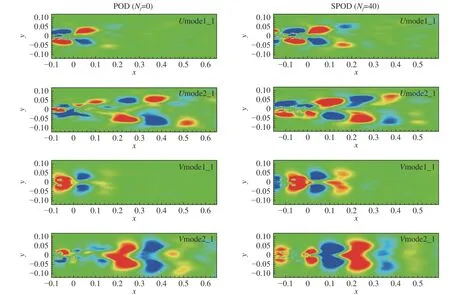
图12 不对称转向架速度U和V的前两对模态云图Fig. 12 Contours of the first two pairs of modes for velocities U and V of the AB configuration

图13展示了对称转向架和无转向架构型速度U和速度V的SPOD(Nf=40)处理前两阶模态的结果。从速度V的模态可知：与不对称转向架的结果对比来看，对称转向架和无转向架构型的涡脱落在展向方向上有向外拉伸、扭转的趋势，模态空间分布较为混乱，这可能是由于不对称转向架的前两阶模态所对应的能量占比更大，因此在模态分解过程中相对来说不易受到其他流场结构的干扰。

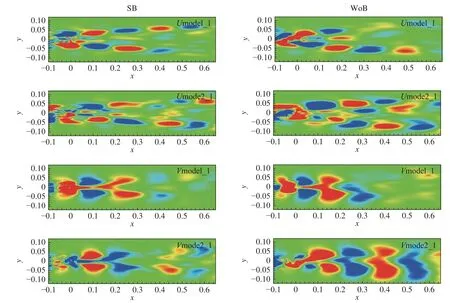
图13 对称转向架和无转向架速度U和V的前两对模态云图Fig. 13 Contours of the first two pairs of modes for velocities U and V of the SB and WoB configurations

图14～图16分别展示了不对称转向架、对称转向架和无转向架三种转向架构型的第一对模态和第二对模态的涡量重构结果。从不对称转向架结果来看，对于第一对模态重构结果，可以看到从近尾迹区的交替涡脱落，向下游发展与流向向涡对相互作用后相融合；对于第二对模态重构结果，T1时刻尾迹的主要特征为正弦式震荡，而T3时刻为交替涡脱落，T2时刻则为二者的一个过渡。因此第一对模态表示交替的涡脱落特征，而第二对模态表示涡脱落与正弦式震荡交替出现的双稳态特征[10]，故两对模态在模态图上差别不大。从对称转向架结果来看，如图15所示，相比不对称转向架，第一对模态重构结果的展向范围更窄；第二对模态的的涡脱落不明显，正弦式震荡也不如不对称转向架强烈。从无转向架结果来看，如图16所示，第一对模态的重构结果也能观察到涡脱落，但在近尾迹区较为混乱，与其他两种转向架差别较大，主要是由于空腔后缘流动分离产生的大尺度涡脱落造成的；第二对模态重构结果的涡脱落和正弦式震荡的强度均介于不对称转向架和对称转向架之间。

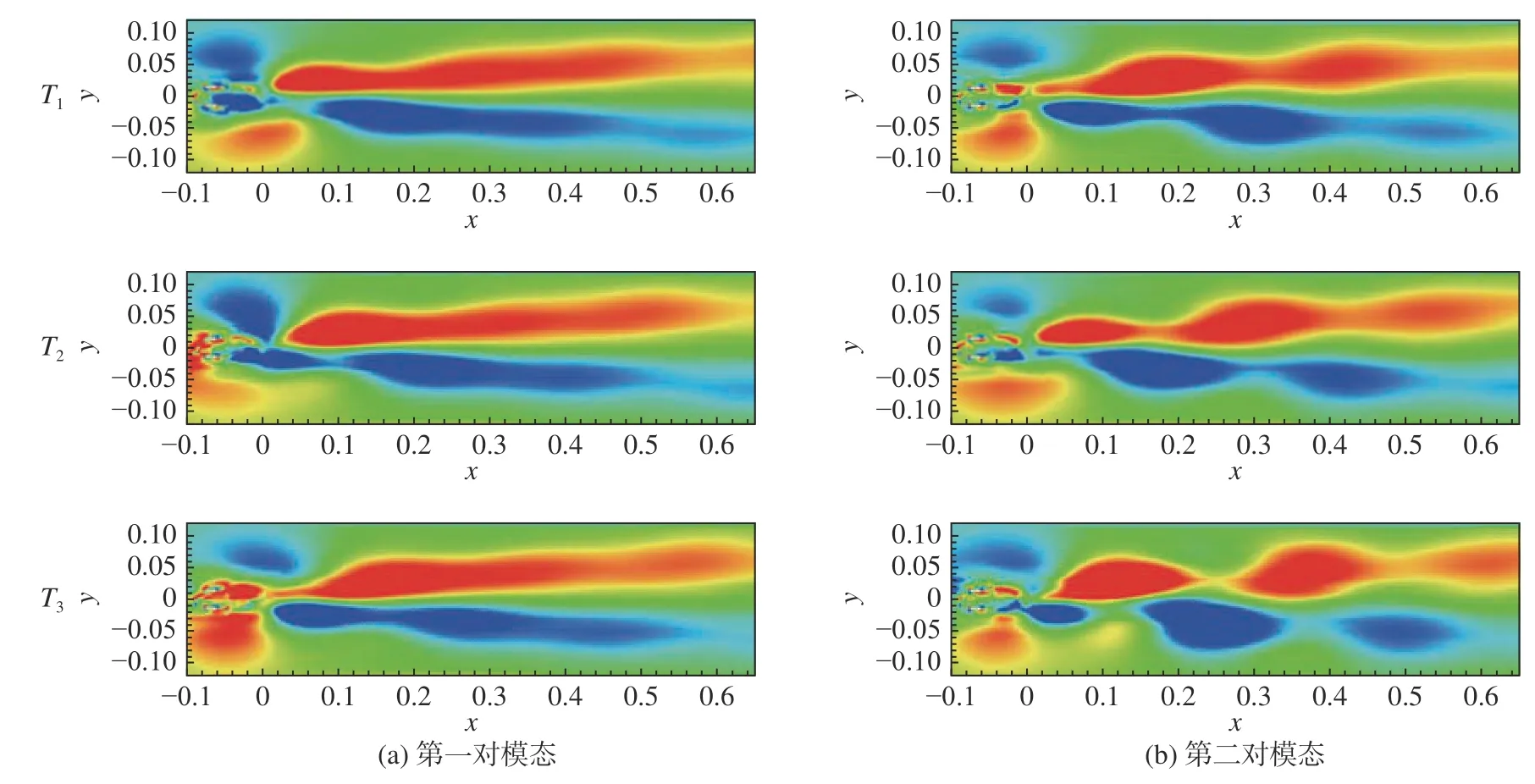
图14 不对称转向架瞬时流场重构结果Fig. 14 Reconstructed instantaneous flow fields for the AB configuration

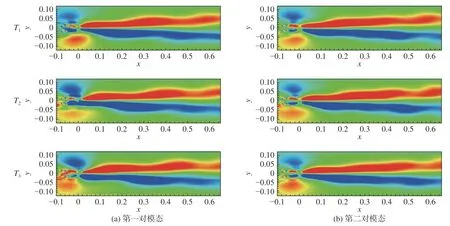
图15 对称转向架瞬时流场重构结果Fig. 15 Reconstructed instantaneous flow fields for the SB configuration

图16 无转向架瞬时流场重构结果Fig. 16 Reconstructed instantaneous flow fields for the WoB configuration

3 结 论

本文采用IDDES数值模拟方法结合SPOD方法研究了三种不同转向架结构对高速列车列车风和非定常尾迹的影响，主要结论如下：

1）三种转向架构型的高速列车尾迹均是由一对反向旋转的半环形流向交替涡脱落主导，当流向涡脱落经过轨道侧和站台侧的测点位置时，会引起较大的列车风速度；

2）对于不对称转向架，由于其不对称结构所带来的扰动与流向涡对较强的相互作用导致交替脱落程度更强，尾涡宽度更宽，进而诱导更高的列车风脉动速度；

3）对于对称转向架，其涡脱落及展向震荡程度均最小，故而列车风在尾迹出现峰值的位置明显延后，时均和脉动速度均最小；

4）对于无转向架，由于空腔后缘的大尺度涡脱落与流向涡对的相互作用，加剧了流向涡对的正弦震荡，扩宽了尾迹宽度，从而产生了最高的列车风时均速度；

5）相比于POD方法，SPOD方法通过对相关矩阵的对角滑动滤波，增强其对角相似性，使得其从复杂湍流中提取主导流动模态的能力更强；随着Nf值的增大，主导模态配对性增强，模态峰值频率更加凸显，模态空间分布更加清晰，但低阶模态能量占比降低。