双圆斑超级混沌吸引系统的数学模型分析及电路实现




摘要:为了研究双圆斑超级混沌吸引系统的非线性动力学行为,首先,提出了其数学微分方程,并进行了数值计算。然后,运用EWB电路仿真软件为系统设计了一个可行的实验电路,研究了系统的非线性动力学行为,给出了系统的周期运动和混沌吸引图像。最后,通过硬件电路实现了该混沌振荡电路。实验结果表明,双圆斑超级混沌吸引系统的动力学数学模型正确有效,数值计算与实验相一致。
关键词:混沌吸引图;数值计算;双圆斑;电路实现
中图分类号:O415.5文献标志码:A
数学家Poincare J.H.于十九世纪初提出Poincare猜想[1],明确指出了混沌问题,推动着动力学系统与拓扑学两大学科领域的融合发展[2]。自从1963年Lorenz在三维自治系统中发现了第一个混沌吸引子以来,人们不断地发现新的混沌系統[3]:在1976 年Rosslor 构造了三维混沌系统[4];1999 年CHEN等在混沌系统反控制中发现了被称为Chen 系统[5-6]的一个新混沌吸引子;2002 年吕金虎等进一步通过混沌反控制想法发现了Lǚ系统[7]及引入一个可变参数,进而提出统一混沌系统[8]。它实现了Lorenz系统和Chen系统之间的过渡;2004 年,一类含有平方非线性项的Liu混沌系统[9]也被提出来。2005年,QI等发现了Qi系统[10-12],这些系统类似但并不拓扑等价。
1984年, Chua发明了著名的蔡氏电路[13]。它首次把电路与混沌两个完全不同的学科相互联姻,强有力地推动了非线性电路理论的加速应用与发展,使人们对混沌理论从认识到深入研究再到工程应用的不同发展深化阶段[14-16]。
混沌现象四十年来倍受众多学科领域学者的关注。它作为非线性动力学系统所特有的混沌现象,广泛地存在于物理学、化学、生物学、地质学等自然界和经济、艺术等社会科学的各领域。混沌同步研究发展迅速,其在图像处理、保密通讯等应用方面取得了巨大的进展[17-18]。二十世纪七十年代,生理学家研究人类心脏、生态学家探索种群增减规律、医学家研究显微镜下观察到的血管缠绕交叉现象、气象学家探究雷电的径迹、天文学家探索星星的簇集效应、经济学家探讨股票价格波动等自然现象和社会现象,发现均存在着混沌非线性现象。混沌控制有很好而广泛的应用远景,它迅速冲进了科学的各个领域,如在电子学、保密通信、流体力学、神经网络、医学、生物系统等领域里形成雪崩式的应用[19-20]。
本研究对一个新的含有3个参数混沌吸引系统模型进行分析、仿真,研究系统的非线性动力学特性,给出系统的周期运动和混沌吸引图像。最后设计实现系统的硬件混沌振荡电路,电路实验结果与动力学特性分析、仿真相同,进一步验证了分析的正确性。研究成果对混沌图像处理技术具有重要的理论意义。
1 双圆斑超混沌吸引系统基本模型及数值仿真研究
1.1 双圆斑超混沌吸引系统基本模型
文中给出的双圆斑超级混沌吸引系统的数学模型是一个三元一次迭代方程组,其动力学方程为
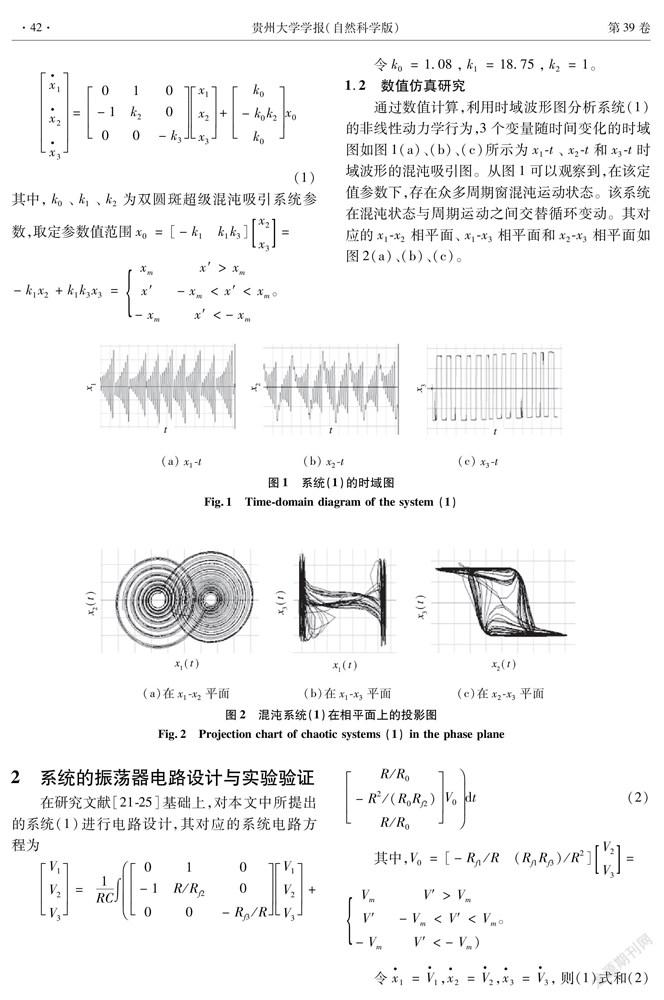
1.2 数值仿真研究
2 系统的振荡器电路设计与实验验证
在研究文献[21-25]基础上,对本文中所提出的系统(1)进行电路设计,其对应的系统电路方程为
3结论
通过以上理论分析、数值计算和实际电路实验,对双圆斑超级混沌系统进行了研究。这个新的混沌系统中存在着复杂的混沌动力学行为,并用电子振荡器电路直观地实现了其动力学行为,电路实现结果与数值计算仿真结果相同,说明该系统电路实现的可取性。它在医学图像处理、保密通信等领域中具有潜在的应用价值。
参考文献:
[1]王开. 确定性随机理论及在混沌密码学中的应用研究[D]. 南京: 东南大学, 2004.
[2] 扶龙香, 贺少波, 王会海, 等. 离散忆阻混沌系统的Simulink 建模及其动力学特性分析[J/OL]. 物理学报: 1-16[2021-09-30]. http: //kns. cnki. net/kcms/detail/11. 1958. O4. 20211103. 1426. 046. html.
[3] 徐启程, 孙常春. 具有复合幂函数和共存吸引子的新混沌系统动力学分析与电路仿真[J/OL]. 计算物理: 1-8[2021-09-10]. http: //kns. cnki. net/kcms/detail/11. 2011. O4. 20210409. 1405. 002. html.
[4] ROSSLER O E. An equation for continuous chaos[J]. Physics Letters A, 1976, 57(5): 397-398.
[5] CHEN G, UEATA T. Yet another chaotic attractor[J]. International Journal of Bifurcation and Chaos, 1999, 9(7): 1465-1466.
[6] CELIKOVSKY S, CHEN G R. On a generalized Lorenz canonical form of chaotic systems via a nonlinear observed approach[J]. International Journal of Bifurcation and Chaos, 2002, 12(8): 1789-1812.
[7] L J H, CHEN G R. A new chaotic attractor coined[J]. International Journal of Bifurcation and Chaos, 2002, 12(3): 659-661.
[8] L J H, CHEN G R, CHENG D Z, et al . Bridge the gap between the Lorenz system and the Chen system[J]. International Journal of Bifurcation and Chaos, 2002, 12(12): 2917-2926.
[9] LIU C X, LIU T, LIU L. A new chaotic attractor[J]. Chaos, Solitons and Fractals, 2004, 22(5): 1031-1038.
[10]QI G Y, CHEN G R, DU S Z, et al. Analysis of a new chaotic system[J]. Physics Letters A, 2005, 352(43500): 295-308.
[11]QI G Y, CHEN G R. Analysis and circuit implementation of a new 4D chaotic system[J]. Physics Letters A, 2006, 352 (43560): 386-397.
[12]王琳, 倪樵, 黃玉盈. Qi四维系统的暂态混沌现象[J]. 动力学与控制学报, 2007, 5(1): 18-22.
[13]CHUA L O, KOMURO M, MATSUMOTO T. The double scroll family[J]. IEEE Transactions on Circuits and Systems, 1986, 33(11): 1072-1118.
[14]L J H, CHEN G R. Generating multiscroll chaotic attractors:theories, methods and applications[J]. International Journal of Bifurcation and Chaos, 2006, 16(4): 775-858.
[15]陈军. 自适应反馈单神经元模型混沌非线性电路实现设计研究[J]. 华中师范大学学报(自然科学版), 2013, 47(3): 335-339.
[16]黄丽莲, 项建弘, 王霖郁, 等. 非线性变形蔡氏混沌电路实验仪[J]. 物理实验, 2019, 39(9): 28-32.
[17]蔡国梁, 谭振梅, 周维怀, 等. 一个新的混沌系统的动力学分析及混沌控制[J]. 物理学报, 2007, 57(11): 6230-6237.
[18]陈军. 外界激发型学习神经元的动力学研究与电路设计实现[J]. 贵州大学学报(自然科学版), 2019, 36(1): 13-20.
[19]陈骏. 不同系统的混沌同步及相关问题的研究[D]. 上海: 上海大学, 2004.
[20]陈军, 李春光. 具有自适应反馈突触的神经元模型中的混沌: 电路设计[J]. 物理学报, 2011, 60(5): 5031-5037.
[21]王东晓, 雷腾飞, 毛北行. 分数阶Sprott-F不确定混沌系统的适应滑模同步[J]. 吉林大学学报(理学版), 2021, 59(2): 384-390.
[22]陈军, 李春光. 禁忌学习神经元模型的电路设计及其动力学研究[J]. 物理学报, 2011, 60(2): 5021-5029.
[23]李德奎. 新四翼超混沌系统的线性反馈控制[J]. 贵州大学学报(自然科学版), 2021, 38(4): 32-35, 44.
[24]GONG L H, WU R Q, ZHOU N R. A new 4D chaotic system with coexisting hidden chaotic attractors[J]. International Journal of Bifurcation and Chaos, 2020, 30(10): 14-21.
[25]朱道宇. 一个新的超混沌系统的叉型分支和复杂动力学[J]. 贵州大学学报(自然科学版), 2017, 34(3): 10-14.
(责任编辑:曾晶)
Mathematical Model Analysis and Circuit Realization of Double
Circular Spot Super Chaotic Attractor System
CHEN Jun
(Department of Medicine Education, Dingxi Campus, Gansu University of Chinese Medicine, Dingxi 743000, China)Abstract: In order to study the nonlinear dynamic behavior of a double-circular spot superchaotic attractor system, the mathematical differential equation was firstly proposed and its numerical calculation was carried out. Then a feasible experimental circuit was designed for the system by using EWB circuit simulation software. The nonlinear dynamic behavior of the system was studied, and the periodic motion and chaotic attraction images of the system were given. Finally, the chaotic oscillation circuit was realized by hardware circuit. The experimental results show that the dynamic mathematical model of the double circular spot super chaotic attraction system is correct and effective, and the numerical calculation is consistent with the experiment.
Key words: chaotic attraction graph; numerical calculation; double circular; circuit realization

