基于椭圆曲线中配对的密码学研究综述*

王 辈, 胡红钢

中国科学技术大学信息科学技术学院中国科学院电磁空间信息重点实验室, 合肥 230027

1 引言

椭圆曲线理论在数论发展史上占有浓墨重彩的一笔, 如怀尔斯利用椭圆曲线给出了费马大定理的证明. 其在应用学科—密码学, 也是一个将抽象数学应用到实际中的最闪亮的范例, 如椭圆曲线密码体制. 此后, 椭圆曲线在密码学上的应用便开始层出不穷. 从学术的角度说, 椭圆曲线对密码学的一大贡献在于它提供了一个用途广泛的数学工具, 也就是具有一定安全属性的双线性映射—配对. 1993 年, Menezes 等人[1]利用Weil 对将椭圆曲线离散对数问题转化到有限域上的离散对数问题, 也就是MOV 攻击. 1999年, Frey[2]等人利用Tate 对给出了椭圆曲线离散对数的另一种约化, 即FR 约化. 除了配对在密码分析的应用外, Joux[3]利用双线性对给出一轮三方密钥交换协议. 然而, 正式将配对发挥重大作用的还要归功于Shamir[4], 他在1984 年提出公钥是否可以为任一字符串, 试图构造基于身份的公钥密码体制, 并提出了两个公开问题: (1) 如何向众多的可信第三方证明自己的身份; (2) 可信第三方如何安全地将用户的私钥送到用户手中. 直到2001 年,Boneh 等人[5]利用Weil 对构造出基于身份的密码体制,才很好地解决了这两个公开问题. 随后, 其他基于身份的密码体制也随之产生, 如数字签名[6,7]、(已认证) 密钥交换协议[8]、变色龙哈希[9]及其在或者不在随机预言机下的层次扩展[10,11]. 其他一些基于配对的方案不是基于身份的, 而是具有特殊功能, 例如秘密握手[12]、短/聚合/可验证地加密/组/环/盲签名[13–17]和签密[18–20].

目前, 计算配对的算法主要有Miller 算法[21]和椭圆网算法[22], 相比之下, Miller 算法的计算效率较高且适应范围更广泛. Miller 算法的主要过程就是计算Miller 函数fr,P, 其中r影响着算法的迭代次数.由于配对的广泛应用, 配对的计算效率需要不断地提高. 研究者们开始从各个角度对此展开研究, 主要分为两大方向: 一是利用理论与算法的工具来改善Miller 算法, 如分母约化技术、选定梅森素数作为r等;二是构造新的更快速的配对, 如构造迭代次数更少的配对. 本文第2 节按时间顺序给出了配对的原始定义与改进方案, 结合研究者们的研究成果介绍近二十年来配对的发展历程. 第4 节简单介绍了Miller 算法的改进算法以及计算多重配对的最新改进算法.

配对友好型曲线的构造也是近些年的一大研究热点, 其构造思想需权衡配对的计算效率与安全性. 本文第四部分简要地介绍了近些年配对友好型曲线的种类, 重点介绍几类最流行的配对友好型曲线—BN 曲线、BLS 曲线和KSS 曲线. 一些国际标准组织在制定基于配对的密码体制相关标准中[23–25], 这三类曲线总是占据主导位置. 我国国家密码管理局在2016 年发布的SM9 标识密码算法, 其中使用的曲线是BN曲线. 目前实现双线性对的一些代码库, 有miracl 库[26]、mcl 库、amcl 库[27]、PBC 库[28], relic 库等.根据最新的文献资料和构造密码方案期望达到的安全级别, 我们总结了以上三类曲线相应参数的选取与参数长度, 以便底层实现的研究者们快速掌握相关数据.

基于身份的密码体制[5]是建立在双线性Diffie-Hellman 假设之下, 此假设包括两大困难问题—双线性Diffie-Hellman 问题与双线性Diffie-Hellman 判定性问题. 双线性Diffie-Hellman 判定性问题强于Diffie-Hellman 计算性问题, 而Diffie-Hellman 计算性问题又强于离散对数问题. 由此可见, 解决这些问题是当前数学界与密码学界的研究热点. 除这些问题外, 还有其他困难问题, 第5 节会具体给出它们的定义, 并简要地介绍其困难程度和配对的安全性研究.

下面我们介绍配对相关理论中一些基本的符号:

2 椭圆曲线中的配对

椭圆曲线是一类亏格为1 的包含一个无穷远点∞的光滑曲线. 设定义在K上的椭圆曲线E满足Weierstrass 方程

密码学者们利用配对设计密码体制时需要考虑使用哪一类配对以及配对的安全性参数等问题, Galbraith[31]给出了此三类配对的安全性比较. Abe 等人[32–34]就此三类配对给出了不同类型的结构保存签名算法. 下面,我们具体介绍椭圆曲线上的各种配对.

2.1 Weil 对

命题3E/K,f,g如命题1,2 所述,设S ∈E[r]是另一个r-扭点,那么对任意点X ∈E,g(X+S)r=f([r]X+[r]S)=f([m]X)=g(X)r. 从而,g(X+S)/g(X)∈μr.

由以上三个命题, 下面我们来给出Weil 对的一种定义.

定义2 设映射

这里选取X ∈E使得g(X+S) 和g(X) 都有定义且非零.

定理1[30]设E/K是椭圆曲线, 存在S,T ∈E[r] 使得er(S,T) 为r-次本原单位根. 特别地, 当E[r]⊂E(K) 时, 有μr ⊂K.

在实际应用中, 为方便Weil 对的计算, 我们一般采用下面的等价定义.

当分母出现零时, 再重新选择R,S, 重复操作直至计算出结果. 这里分母为零的可能性很小(发生的概率至多为O(logp/p)). 因此, 此表达式(4) 在很大的概率上是合理定义的.

命题4[30]设P,Q ∈E[r], 则¯er(P,Q)=er(P,Q).

命题5[29]Weil 对具有如下性质:

· 双线性, 非退化, 见定义1;

· 交互性:P ∈E[r], 满足er(P,P)=1. 利用双线性, 则有er(P,Q)=er(Q,P)-1;

· 相容性: 若P ∈E[rr′],Q ∈E[r], 则err′(P,Q)=er(r′P,Q);

· Galois 作用:P,Q ∈E[r],σ ∈Gal(¯K/K), 则有er(P,Q)σ=er(Pσ,Qσ).

根据Weil 对的交互性, 当Q=kP时, 总有¯er(P,Q)=1, 从而在实用中并不安全. 密码学上使用的Weil 对一般为改进的Weil 对,具体定义为ˆer(P,Q)= ¯er(P,φ(Q)),可见文献[5,35]. 其中φ ∈End(E)满足φ(Q)∈＜P ＞,φ称为distorsion 映射. 对于distorsion 映射的存在性, 可参见文献[36,37]. Cheol[38]给出了Weil 对的一种改进办法: 对于改进的Weil 对ˆer(P,Q), 当φ为单射且可分时, 可以将扩域上运算约化到基域上处理, 从而加快了配对的计算. 特别地, 当P=Q, ˆer(P,P) 的计算可约化成Tate 对的形式(仅需一个Miller 函数fr,P) 且没有指数步的计算.

2.2 Tate 对

Tate 对是另一类经典的双线性非退化的映射. 最早在1958 年由Tate 提出, 之后Lichtenbaum 做了进一步的扩充. 1994 年, Frey 和Rück[39]首先分析了任意阿贝尔簇的除子类群上的离散对数, 利用Tate对将其约化到有限域或者局部域的剩余类域上的离散对数. 1998 年, 他们[2]又给出了有限域上的椭圆曲线离散对数的约化. 下面我们仅给出椭圆曲线上Tate 对的定义与结论, 从它与Weil 对的关系出发, 结合研究者的改进方法一步步给出它的改进定义.

一些研究者给出了Tate 对在其他曲线形式下的计算, 比如Jacobi Quadratic 曲线[42]、Edwards 曲线[43,44]、超椭圆曲线[45,46]. Duursma 和Lee 等人[45]在超椭圆曲线上提出了Tate 对的改进办法—减少迭代次数, Barreto 等人[46]正是根据这个思想在超奇异椭圆曲线上构造了新的配对—Eta 对, 它的计算效率比Tate 对的快. 在这之后, 新的配对大量涌现, 但是总体上, 这些新的配对均是将Tate 对限制到某些特定子群上构造的.

2.3 Eta 对与Ate 对

这里, 我们主要介绍两个特殊的Tate 对, 现已被广泛应用与研究.

这里T=t-1,P,Q ∈E(Fq)[r]. 在一定的条件下, 此配对是非退化双线性的. 当r ≈#E(Fq) 时, Eta 对的迭代次数几乎比Tate 对的的迭代次数少一半.

Eta 对的定义在一般椭圆曲线上并不适用, Hess 等人[47]进一步将Eta 对扩充到一般椭圆曲线上, 构造了Ate 对与Twisted Ate 对. 下面, 我们分别给出它们的定义.

引理1[30]设E/Fq是椭圆曲线,r为大素数且满足r| #E(Fq),k为与r对应的嵌入次数. 则E[r]⊂E(Fqk).

设πq是椭圆曲线E上的Frobenius 自同态.πq的特征多项式为h(u) =u2-tu+q,h(u)≡(u-1)(u-q)modr, 则0≡(πq-1)(πq-q)modr.

引理2[40]πq在E[r] 上形成两个特征子空间, 分别是1-特征子空间G1=E[r]∩ker(πq-[1]) =E(Fq)[r] 和q-特征子空间G2=E[r]∩ker(πq-[q])⊂E(Fqk)[r]. 很显然,G1,G2是加法群且有E[r] =G1⊕G2.

Wang 等人[53]根据αtwist的定义, 通过Weierstrass 型曲线和Edwards 型曲线之间的映射关系在高次扭Weierstrass 曲线上定义了一个新的配对T-Ate 配对, 结合了Edwards 型曲线的快速点加倍点运算和Weierstrass 型曲线的Miller 快速计算公式.

显然, 当t比较小时, Ate 对和扭Ate 对比Tate 对的计算要快. 但是, 并不是所有的配对友好型曲线都具有较小的迹t. 已知T ≡qmodr且r‖qk-1, 则r|Φk(T)(其中Φk为分圆多项式), 那么T的极小值为r1/φ(k)(φ为欧拉函数). 所以Ate 对的Miller 迭代次数的下界是log(r1/φ(k)). 对于一些配对友好型曲线, 这个下界是可以达到的, 如分圆类椭圆曲线[54,55]. Duan 等人[56]改进了文献[54] 中的方法, 当k=2i·3 时, 构造一类椭圆曲线满足t ≈r1/φ(k). Lin[57]进一步分析k=3i的情况, 构造了t ≈r1/φ(k)的一类椭圆曲线并给出了k=9 时Ate 对的快速计算. 所以改进Ate 对与扭Ate 对的主要研究方向就是使Miller 迭代次数尽量达到下界, 下面§2.4 节我们会给出这一研究方向的具体进展. 由于改进Ate 对的方法对扭Ate 对同样适用, 下面我们仅针对Ate 对的研究作分析.

2.4 其它配对

Matsuda 等人[58]构造了优化Ate 对, 他们把T=t-1(≡qmodr) 换成任意的整数S ≡qmodr.这样构造的新的配对比Tate 对至少快两倍. 文献[59] 给出了优化Ate 对在分圆类椭圆曲线上的计算, 文献[60] 给出了优化Ate 对的在BN 曲线上的快速实现算法. Zhao 等人[61]延续了Matsuda 等人的思想,继续减少Miller 的迭代次数, 构造了广义的Ate 对Atei, 定义如下.

定义9 设E/Fq是椭圆曲线,r为大素数且满足r|#E(Fq). 设k为嵌入次数且T=t-1, 我们令Ti=Ti ≡qimodr,1≤i ≤k-1. Q ∈G2⊂E[r]∩ker(πq-[q]),P ∈G1=E[r]∩ker(πq-[1]). 广义的Ate 对(Atei对) 定义如下:

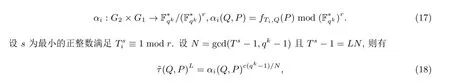
同样, 我们可以给出定义在G2×G1上的R-Ate 对RA,B(Q′,P′), 其中Q′∈G2,P′∈G1. 当(A,B) =(qi,r) 时,RA,B(Q′,P′)=fTi,Q′(P′), 从而Atei对是特殊的R-Ate 对.

对一些之前不能达到下界的配对友好型曲线, 若在其上计算R-Ate 对, 它的迭代次数却能达到下界log(r1/φ(k)). 而且文献[64] 表明计算R-Ate 对比计算Atei对的整体消耗节省29%-69%. 结合Ate 对与几类改进的Ate 对, 在一些曲线上, 他们的迭代次数均可以达到下界. Vercauteren[63]将这些Miller迭代次数可以达到下界的配对命名为最优配对(optimal pairing), 定义如下.

定义11 设e:G1×G2→GT是一个非退化双线性配对, 并且|G1|=|G2|=|GT|=r, 其中GT定义在域Fqk上. 若配对的Miller 迭代次数≈log(r1/φ(k))+ε(k),ε(k)≤log(k), 则称此配对e(·,·) 为最优配对.

这个定义并不仅仅对于配对中只有一个Miller 函数的配对满足要求, 例如Ate 对, 对于配对中有几个Miller 函数的乘积或者线性组合, 其计算的总Miller 迭代次数也满足要求, 例如R-Ate 对. 以上分析可知Ate 对及其改进Ate 对在特定情形下可以成为最优配对. 那么, Weil 对或者扭Ate 对, 他们会是最优配对吗? Vercauteren[63]给出了一个假设: 除具有有效可计算自同态(Frobenius 自同态除外) 的椭圆曲线, 其上的任意非退化配对, 迭代次数均可达到下界log(r1/φ(k)). Hess 等人[65]证明了这个猜想, 证明的主要思想是将配对的Miller 函数表示为一系列次数较小的函数的乘积, 并利用格的相关工具证明了配对的迭代次数在理论上可以达到下界log(r1/φ(k)). 他们的结论对Weil 对、Ate 对和扭Ate 对均成立. 到目前为止, 最快的配对是最优Ate 对(optimal Ate pairing), 而且在实际中被广泛应用.

自配对的定义首先由Lee[66]提出, 他在秩为2 的自由模上定义了自配对A×A →A, 并将其推广到椭圆曲线上, 定义了E[r]×E[r]→E[r]. 这一类椭圆曲线上的自配对与Weil 对有很多相似的性质, 并且可以建立密钥协商与数字签名算法. 然而, 更常用的自配对是椭圆曲线上对于同一点的自配对es(P,P).事实上, 自配对就是在以往配对的基础上再定义的配对, 如es(P,P) =e(P,φ(P))(自配对与Weil 对的关系). 文献[67-69] 给出了自配对在椭圆曲线与超椭圆曲线上的快速计算. 值得一提的是, 相比Tate 对或者Ate 对的最终指数步计算, 自配对的指数步计算更快速. 这一类的自配对es(P,P) 目前在密码学上应用广泛, 如短签名[17]、在线/离线的签名体制[70]、基于身份的Chameleon 的哈希方案[71].

本文所有配对的定义均是在椭圆曲线上讨论的, 文献[64,73-75] 给出了一些配对在超椭圆曲线上的定义. 相比较于椭圆曲线, 超椭圆曲线具有更丰富的自同态环结构, 能否利用其自同态环中的某些特别元素加快超椭圆曲线上的双线性对有效计算或构造具有更短Miller 链的双线性对? 目前, 适于双线性对的超椭圆曲线并不多, 如何构造更多配对友好型超椭圆曲线值得进一步研究.

3 配对友好型曲线及参数选取

关于求解变量(u,y) 的整数解. 参数化的配对友好型曲线更具体的定义如下:

定义13 设t(u),r(u),q(u)∈Q[u]. 给定正整数k和非平方正整数D, 若以下条件满足

(1)q(u)=p(u)d,d ≥1,p(u) 代表素数;

(2)r(u) 是非常量的、不可约的、表示整数值的且首项系数大于0;

(3)r(u) 整除p(u)+1-t(u);

(4)r(x) 整除Φk(t(u)-1), 其中Φk表示k次分圆多项式;

(5) 方程Dy2(u)=4q2(u)-t2(u) 有无数整数解(u,y).则称三元组(t(u),r(u),q(u)) 表示具有嵌入次数k和判别式D的一类椭圆曲线. 同样, 对于某一类椭圆曲线, 其ρ的定义如下:

注2 对于有理系数多项式g(u) 满足四个条件, 则可表示为素数: (1) 非常量的不可约多项式; (2) 首项系数大于0; (3) 对于某些u ∈Z,g(u) 表示整数; (4) 对于某些u1,u2∈Z, 有gcd(g(u1),g(u2))=1.

某一类椭圆曲线构成集合的基数取决于变量(u,y) 的整数解的个数. 在某些情况下, 若解(u,y) 组成的集合呈指数增长, 我们称这样的类为稀疏的. 在其他情况下, 若解(u,y) 组成的集合相当稠密, 我们称这样的类为完备的.

Freeman 等人[76]对近些年配对友好型曲线作了详细综述, 主要分为非参数化的配对友好型曲线和参数化的配对友好型曲线. 非参数化的配对友好型曲线主要包括: 超奇异椭圆曲线伴随嵌入次数k ∈{1,2,3,4,6}, 见文献[76, §3]; Cocks–Pinch 曲线[77]; DEM 曲线[78]. 参数化的配对友好型曲线包括: 稀疏的类和完备的类. 目前稀疏的类有: MNT 曲线类伴随嵌入次数k ∈{3,4,6}[79]; GMV 曲线类—扩展的MNT 曲线类[80]; Freeman 曲线类伴随嵌入次数为k= 10[81]. 目前完备的类有: 分圆域类—包括BLS 曲线[55]和BW 曲线[54]; 零星类—包括BN 曲线[82]; Scott–Barreto 类[83,84]. 目前在实际应用中(如NIST 或者国密算法SM9 中) 较广泛被使用的曲线有BN 曲线、BLS 曲线、KSS 曲线[85](BW 曲线的一些特例). 下面我们重点介绍这三类曲线相关参数的选取.

3.1 BN 曲线

BN 曲线是定义在有限域Fp,p ≥5 上的椭圆曲线E, 它的阶r和特征p均是参数化的素数

其中u是精心挑选的整数.E的曲线形式为y2=x3+b, 其中b ∈F*p. BN 曲线的嵌入次数k=12.

注意, BN 曲线总是有6 阶扭曲线: 若ξ ∈Fp2既不是二次剩余也不是三次剩余, 则定义E的扭曲线E′/Fp2满足y2=x3+b′, 其中b′=b/ξ或b′=bξ. 为了简化计算, 元素ξ可用Fp12在Fp2上的六次扩张的本原元来表示, i.e., Fp12= Fp2[γ],γ6=ξ. 顺便说一下, BN 曲线已成为许多近期出版物的热点, 比如文献[52,86-90].

3.2 BLS 曲线

BLS 曲线和BN 曲线的定义很相似, 也是定义在参数化的特征p上且满足方程y2=x3+b′的曲线.与BN 曲线不同的是, BLS 曲线的阶不是素数阶的, 其阶可被一个很大的参数化的素数r整除, 从而可以在r阶扭子群上定义配对. 它们可使用不同的嵌入次数, 但研究者们关注最多的是BLS12 和BLS24, 其相对于r的嵌入次数k分别为12 和24. 具体参数由下式给出.

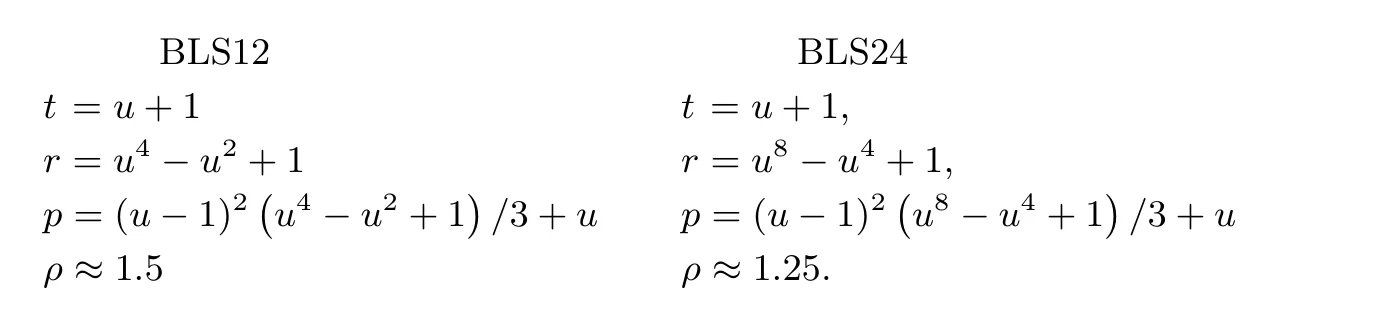
其中u是精心挑选的整数.

3.3 KSS 曲线

KSS 曲线也可用于不同的嵌入度. 若嵌入次数k= 18, 其与BLS 曲线非常相似(曲线方程表达式,同样有6 次扭曲线, 参数化素数p和r|#E(Fp)). 在这种情况下, 参数表示如下:

4 计算配对的算法总结

本节我们总结计算配对的一些算法,主要有Miller 算法[21]和椭圆网算法[22]. Stange[22]于2007 年利用椭圆网(椭圆除序列) 的性质给出了一种计算Tate 对的多项式时间算法, 该算法也适用于Weil 对的计算. 但与Miller 算法相比, 该算法的效率仍然较低. 而且Miller 算法的适用范围要比Stange 算法广泛.但是Stange 算法的优势在于计算过程中无需求逆操作, 因此该算法依然值得进一步优化. 本节, 我们着重介绍Miller 算法及其改进算法, 它的算法的基本步骤包括Miller 迭代步(MLP) 和最后的指数步(FE),其中关键步骤是计算Miller 函数fT,Q(这里假设计算Ate 对,Q ∈G2). 由于Miller 函数fT,Q满足迭代关系:

算法1 Miller 算法计算Miller 函数fT,Q Input: r ∈N, P ∈G1,Q ∈G2 Output: fr,Q(P)1 T = ∑l j=0 tj2j, tj ∈{0,1} 且tl = 1.2 R ←Q, f ←1 3 for j = l-1 →0 do 4f ←f2gR,R(P), R ←[2]Q;5if tj = 1 then f ←fgR,Q(P), R ←R+Q;7end 8 end 9 Return f.6

(2) 在一些特殊的椭圆曲线上改进配对的计算, 如MNT 曲线[41,79,95], BN 曲线[52,96];

(3) Miller 迭代包括点的加法与倍乘运算, 分析在不同的坐标系下加快点的运算[97];

(4) 当嵌入次数为偶数时, 可采用分母约化的技术加快运算[41];

(5) 从算法的角度对r分析, 如选取r为梅森素数减少Miller 迭代的次数, 将r做NAF 或者NAFw展开[98]等;

(6) 利用distorsion 映射在超奇异椭圆曲线上改进Tate 对[46].

(7) 将椭圆曲线密码体制中的点压缩技术应用到配对计算中, 加快配对的计算, 这一思想, 首次由Scott 和Barreto 实现并提出压缩双线性对的概念[99].

(8) 对于具有高次扭曲线的曲线, 利用高次扭将点加与倍点运算降到更小的域上计算, 从而加快配对的加算效率, 主要针对Ate 对或者optimal Ate 对[48,49].

国际标准中大多使用BN 曲线或者BLS 曲线上的optimal Ate 对, 主要这两类曲线上的配对计算效率较快, 而且都具有六次扭曲线. 所以上面的第八种改进方法可以被采用. 结合Ate 对的定义(§2.3) 和注1 中的具体分析, 我们给出计算optimal Ate 对的改进算法, 见算法2. 算法2 只是表达了具体改进的思想, 对于BN 曲线上optimal Ate 对利用扭曲线改进的精确表达, 可参见文献[96, Alg 1].

算法2 利用扭曲线改进的Miller 算法计算optimal Ate 对Input: T ∈N, Q′ ∈G′2, P ∈G1, Q′ 与P 线性无关Output: αopt(Q,P) = fT,φ(Q′)(P)qk-1 1 T = ∑l j=0 tj2j, tj ∈{0,1} 且tl = 1.r 2 R′ ←Q′, f ←1 3 for j = l-1 →0 do 4f ←f2gφ(R′),φ(R′)(P), R′ ←[2]R′;5if tj = 1 then f ←fgφ(R′),φ(Q′)(P), R′ ←R′ +Q′;7end 8 end 9 f ←f(qk-1)/r 10 Return f.6

由于多重配对越来越高的关注度, 加快多重配对的计算效率也是一研究要点. 研究者们发现调整单个配对实现可以在多重配对实现中有效工作, 这绝不是微不足道的发现. 因而一些在单个配对计算上的优化在多重配对计算上变得可用, 而且研究者们[100–102]得到—两个配对乘积的联合计算比计算两个单独配对的乘积更快. 最近, Scott[103]对传统的Miller 算法拆分成两个算法, 一个算法计算和存储g函数, 另一个算法计算Miller 函数f. 注意到他的算法主要针对BLS12 曲线上的Ate 对的实现, 根据有限域Fp12的特殊表示, 垂直方程υ的计算在Ate 对的计算中不产生影响, 所以Miller 函数fT,Q的计算只与线性函数l有关, 从而Miller 算法可以拆成两个算法. 具体见算法3 和4.

算法3 计算和存储BLS12 曲线上Ate 对的g 函数Input: T ∈N, Q ∈G2, P ∈G1 Output: 在Fp12 上的长度为■log T」 的数组g,1 T = ∑l j=0 tj2j, tj ∈{0,1} 且tl = 1.2 R ←Q, f ←1 3 for j = l-1 →0 do 6 4g[i] ←lR,R(P), R ←[2]R;5if tj = 1 then g[i] ←g[i]lR,Q(P), R ←R+Q;7end 8 end 9 Return g.

正如Scott[103]所说, 这种拆分的Miller 算法只有在计算多重配对时才能体现出它的优势, 他相继也给出了计算多重Ate 对的数组g算法和计算Miller 函数f的算法, 相似于算法3 和4, 这些算法已在amcl 库[27]中实现. 更重要的, 针对BLS12-381 的多重Ate 对的计算消耗, 他给出进一步分析, 计算单个Ate 对需要1556m, 计算双重Ate 对需要1797m, 而计算高于双重的Ate 对仅需要1856m, 其中m表示一个乘法操作. 由此可见, 此种拆分算法的优势所在.

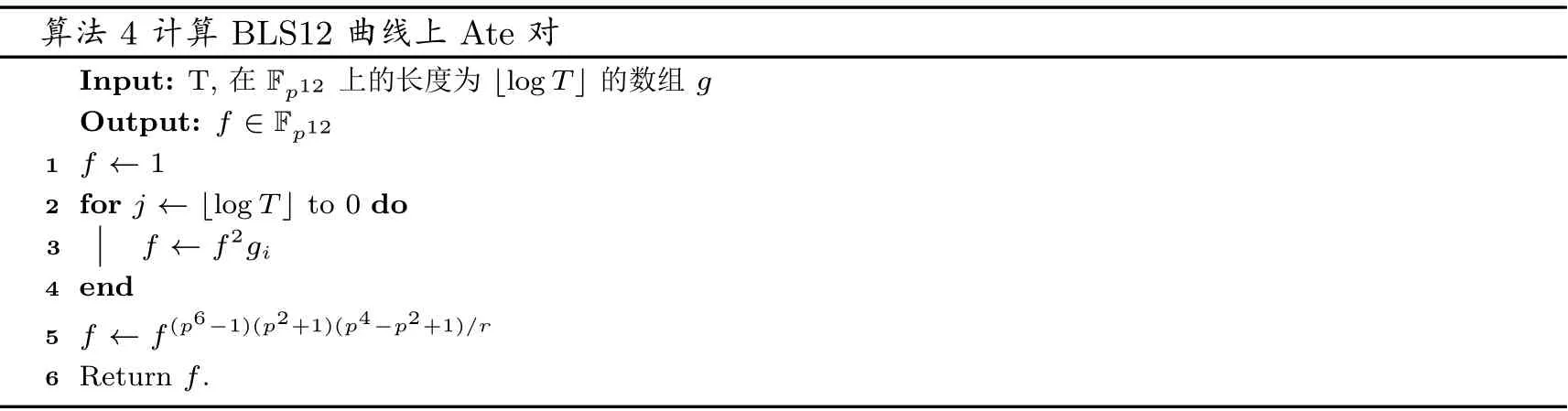
算法4 计算BLS12 曲线上Ate 对Input: T, 在Fp12 上的长度为■log T」 的数组g Output: f ∈Fp12 1 f ←1 2 for j ←■log T」 to 0 do 3f ←f2gi 4 end 5 f ←f(p6-1)(p2+1)(p4-p2+1)/r 6 Return f.

5 与配对相关的计算困难问题与安全性研究

基于配对的密码体制的安全性主要基于以下困难问题的假设:

· 离散对数问题(discrete logrithm problem (DLP)): 这里给出有限域上离散对数的定义. 考虑Fq的乘法群F*q: 设x,y ∈F*q, 满足xm=y, 求解mmod ord(x).

· 椭圆曲线离散对数问题(ECDLP): 设P,Q ∈E(Fq), 满足Q=[m]P, 求解mmod ord(P).

· 判定性Diffe-Hellma 问题(DDHP):区分四元组{g,gx,gy,gxy|x,y为随机数}与{g,gx,gy,gz|x,y,z为随机数}的分布.

· 椭圆曲线的判定性Diffe-Hellma 问题(ECDDHP):区分两个四元组{P,[a]P,[b]P,[ab]P}与{P,[a]P,[b]P,[c]P}的分布, 其中a,b,c ∈F*q且随机.

· 椭圆曲线的Diffe-Hellman 计算性问题(CDHP): 已知三个点P,[a]P,[b]P ∈E(Fq), 求解[ab]P.

· 双线性Diffe-Hellma 问题(BDHP): 对于四元组{P,[a]P,[b]P,[c]P}, 计算e(P,P)abc.

· 判定性双线性 Diffe-Hellma 问题 (DBDHP): 区分四元组{[a]P,[b]P,[c]P,habc}和{[a]P,[b]P,[c]P,hr}的分布, 其中h=e(g,g),a,b,c,r为随机数.

· 双线性映射的逆问题(pairing inversion):

(1) FAPI (fixed argument pairing inversion): 在定义1 中, 给定a ∈G1和z ∈GT, 计算b ∈G2使得e(a,b)=z. 或者, 给定b ∈G2和z ∈GT, 计算a ∈G1使得e(a,b)=z.

(2) GPI(generalized pairing inversion): 对给定z ∈GT,计算a ∈G1和b ∈G2使得e(a,b)=z.

离散对数问题是建立公钥密码体制的基础, 所以如何找到快速攻击DLP 的算法是当前研究的热点问题. 对于解有限域上离散对数问题(DLP) 的算法主要有次指数时间的指标积(index calculus) 算法[104],在使用指标积方法攻击离散对数时主要用到两种筛法收集线性关系: 数域筛法(NFS)[105,106]和函数域筛法(FFS)[107–109], 2014 年Joux[110]对DLP 研究的发展作了详细的介绍. 这两种筛法适用于不同特征的有限域, 一般地, 对于非小特征的有限域使用数域筛法, 对中间特征或小特征的有限域使用函数域筛法会得到更好的结果. 对于解ECDLP 的算法有大步小步算法[111]、Pollard-ρ算法[112]以及指标积算法[113], 2016 年Galbraith 和Gaudry[114]对ECDLP 研究的发展作了详细的介绍.

以上很多问题大都是建立在DLP 基础上的, 如DDHP、CDHP、BDHP 等. 由于双线性对的快速计算, 椭圆曲线的ECDDHP 是容易的. Dan Boneh 等人[5]利用Weil 对建立了基于身份的密码体制, 其机制的安全性是建立于BDHP 与DBDHP 的困难性. Joux[115]提出了了两类双线性映射的逆问题FAPI与GPI, 并分析以上问题的强弱联系. Cheon 等人[116]利用Lee[66]中的自配对也给出以上问题的强弱关系. 关于FAPI 与GPI 的相关研究可参见文献[117-120]. Kanayama 等人[118]在广义的Ate 对Atei上分析了FAPI 问题, Kim 等人[120]进一步分析了FAPI 问题在Tate 对与Ate 对(及其改进的Ate 对)的困难程度. 表面上, Ate 对比Tate 对的迭代次数小, 代数结构好, 很容易认为Ate 对上的FAPI 问题会弱于Tate 对上的. 然而, Kim 等人[120]发现它们的困难程度等价. 到目前为止, 还无法确定FAPI 问题的困难程度, 也没有它的快速攻击算法, 所以它的安全性依然值得研究.

5.1 配对的最新安全性参数

我们知道构造配对友好型曲线需要权衡(trade-off) 配对的计算效率与安全性. 而定义在有限域Fq上具有嵌入次数k和r阶扭子群的配对, 其配对的安全性由下面两方面决定:

(1) 椭圆曲线E/Fq的r阶扭子群或者商群的离散对数问题的时间消耗(曲线方面);

(2) 有限域Fqk乘法群的子群的离散对数问题的时间消耗(有限域方面).

有限域方面的安全级别评估就相对困难, 因为目前有限域上离散对数的最好攻击算法是指标积算法,然而它的时间复杂度很难精确表达. 自2013 年以来, 一些更复杂的算法[121,122]取代了经典的Coppersmith 算法[123]和函数域筛法[107–109], 它们对小特征域上的离散对数进行了攻击, 使得那些小特征域上的配对无效. ENISA 立即做出了反应, 并在其2013 年发布的标准文件中[124]表示该机构禁止使用小特征的配对. 在非小特征的情况下, 最著名的算法是数域筛法, 自2013 年以来, 也出现了一系列新的变体和改进[125–131]. 扩展域塔的数域筛法[132,133](SexTNFS 算法) 显著改变了攻击的复杂性, 并在同一篇文章中对BN128 的安全性作了精确分析, 表明必须重新评估密钥大小.

紧接着, Menezes 等人[134]和Barbulescu 等人[135]通过分析数域筛法(NFS) 的最新进展对配对的安全性提出了新的估计, Barbulescu 等人[135]的估计更精确. 他们就是利用目前最好的SexTNFS 算法去攻击最流行的配对(BN 曲线上的optimal Ate 对), 发现大多数现有实现中使用的BN128 曲线所能达到的安全级别最多100-bit 安全, 并不是之前所称的128-bit 安全. 并且zk-SNARK[136–139]中被广泛使用的曲线BLS12-381, 在zcash 的安全审计报告中指出其安全级别也未达到其所称的128-bit 安全. 基于这些发现, Barbulescu 等人[135]为几类较流行的曲线在不同安全级别下重新配置了参数, 如参数u的选取、域的大小、曲线的方程. 表1 仅给出曲线中参数u和域Fpk的长度. 对于192-bit 的情况, 表1 对比之前的参数长度[90], 明显可见参数长度的变化. 对于192-bit 和256-bit 安全级别, 这里仅需考虑BLS24和KSS18 曲线, 因为毫无疑问, BN、BLS12 和KSS16 曲线对应域的长度会变很大, 计算效率会降低.

表1 不同安全级别下的不同曲线的参数长度Table 1 Parameter length for different curves at different security levels

注3 在64-bit 多处理器的计算平台上, BN128 曲线上的optimal Ate 对的计算效率最快. 在192-bit 安全级别下, 文献[90,94] 给出了不同曲线上optimal Ate 对在实现上的计算效率, BLS12 曲线上的optimal Ate 对计算效率最快. 注意这些实现效率均是在之前的曲线参数下考虑的. 所以在Barbulescu 等人[135]重新配置的曲线参数之后, 研究者们需分析不同安全级别下的最新曲线参数的配对实现效率.

6 结论

本文从椭圆曲线的Weil 对开始, 结合配对在密码学上的进展, 给出了各类配对的详细定义及其改进方案. 对于初学者来说, 可以较快地了解这方面的工作. 其次, 针对最流行的几类配对友好型曲线, 结合最新的攻击算法, 我们总结了这几类曲线不同安全级别下最新的参数选取, 方便底层实现的研究者们快速掌握. 对于配对上的计算困难问题, 日前研究进展依然缓慢. 我们这里关注的配对只是椭圆曲线上的双线性配对, 对于其他形式的配对并没有作过多关注. 纵观近三十年配对在密码学上的应用, 近二十年来, 研究者们更多地关注配对的快速计算及其改进, 目前理论上可以证明最优配对的存在性, 但在实用中只有很少的配对友好型曲线可以构造出最优配对. 配对在密码学上的应用日益广泛, 它的潜能还有待继续挖掘.