厚度梯度型负泊松比蜂窝抗爆炸特性及优化
孙魁远,孙晓旺,张宏伟,王显会,彭 兵,张绍彦
(1.南京理工大学 机械工程学院,南京 210094;2.内蒙古第一机械集团股份有限公司, 内蒙古 包头 014032)
1 引言
在非对称局部战争环境下,军用车辆底部面临最具代表性的威胁来自于简易爆炸装置(improvised explosive device,IED)和地雷[1]。在爆炸发生时,强烈的冲击波会使车辆地板发生一个明显的向乘员舱侵入的弹塑性变形,严重时可能导致舱室穿透[2]。车辆地板的变形会严重影响到车内乘员的人身安全[3]。因此,对于军用车辆底部防护组件的研究很有意义。
负泊松比材料具有优良的剪切模量、断裂韧性等独特力学性能[4]。孙晓旺等[5]研究了负泊松比铝蜂窝结构在防雷组件中的应用,负泊松比铝蜂窝结构在防雷过程中能吸收大量能量,对车身结构及乘员安全起到很好的保护作用。杨德庆等[6]研究了星型负泊松比结构的抗水下爆炸性能,负泊松比蜂窝相比与常规防护结构具有良好的水下抗爆炸性能。随着功能梯度概念的提出[7],与传统材料相比,功能梯度多孔材料在受到面内冲击作用时,其动态响应和变形模式会随着梯度的变化而在局部发生变化[8]。具有功能梯度变化的结构相较于均质结构在抗冲击性能等方面拥有较大的优势。罗小丽等[9]对比不同厚度梯度结构对车辆抗爆炸冲击性能的影响,结果表明具有厚度梯度的结构,对爆炸冲击的缓冲作用更明显。
Liu等[10]研究了功能梯度封闭泡沫铝芯的全金属夹层板的动力响应和抗爆性能,并与未分级单层板进行了比较,在相同的空气爆炸载荷作用下,分级板的中心横向挠度较小,抗爆炸性能较好。Li S等[11]进行了分层蜂窝铝芯的金属夹芯板在爆炸载荷作用下的有限元仿真,在相同加载条件下,分级夹芯板,特别是相对密度下降的芯材布置,在一定的载荷范围内比未分级夹芯板具有更好的抗爆性能。研究人员前期做了一些功能梯度材料的分析研究,但很少针对负泊松比芯层做功能梯度研究,也没有将负泊松比芯层与功能梯度联系在一起应用到车辆底部防护组建的防爆性能研究上。
本文建立了可以模拟车辆底部爆炸的爆炸冲击台架。基于均质负泊松比蜂窝芯层的防护组件,提出几种厚度梯度型负泊松比蜂窝芯层的防护组件方案,并对它们在同等质量条件下的防护性能作出评估。最后,对厚度梯度型负泊松比蜂窝芯层进行材料结构一体化的多目标优化设计。
2 防护组件台架爆炸试验及仿真对标
2.1 防护组件台架爆炸试验
该台架试验所针对的对象是某车辆底部防护组件,按AEP-55标准的2b等级进行试验。爆炸物是2 kg当量的TNT,位于台架底部正中心,填埋于规定硬质土壤表面下100 mm处,如图1所示。
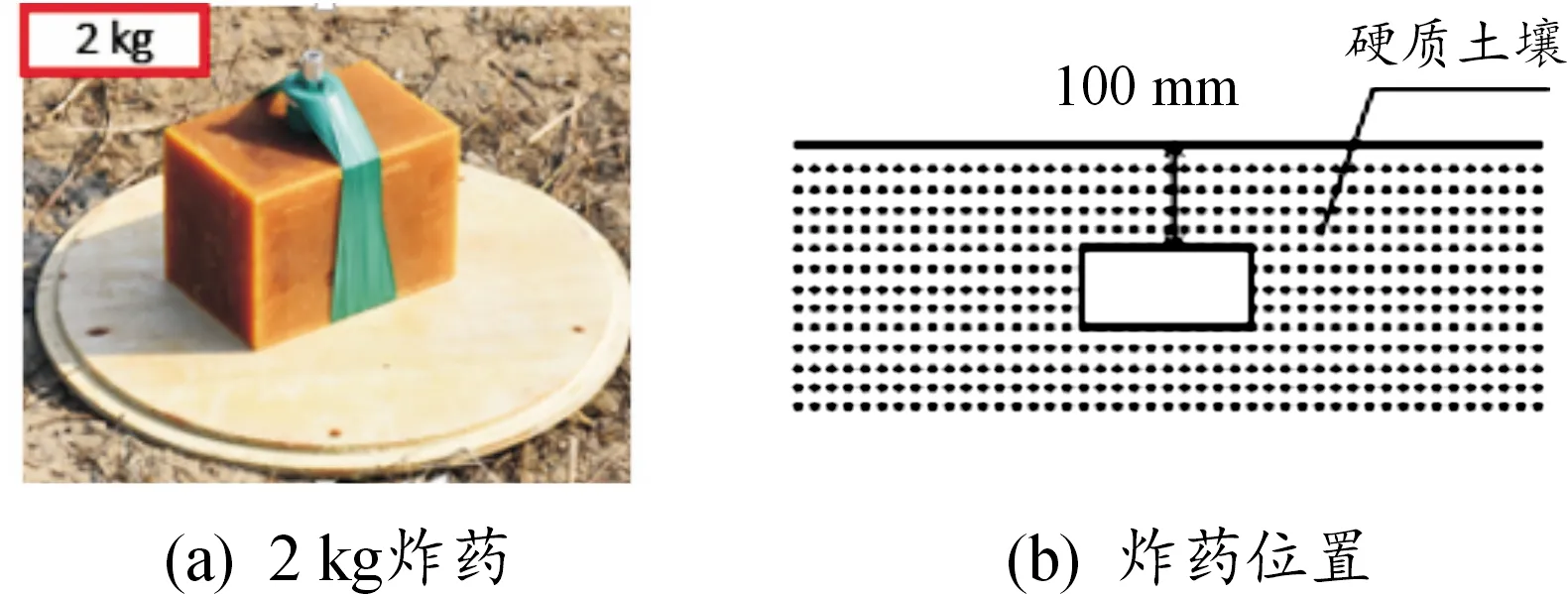
图1 炸药及炸药位置示意图Fig.1 TNT and explosive position
模型的连接方式采用焊接,模型主要组成部件包括:横梁、纵梁、面板、背板、基板、配重块等。台架的整体尺寸为1 860 mm×1 500 mm×760 mm,支撑台架的纵梁和横梁都是10 mm厚的Q235钢,面板和背板分别是10 mm厚和8 mm厚的NP500防弹钢,基板是8 mm厚的960E钢,在面板和背板之间有一个用来提高防护组件整体强度的工字梁,工字梁的长、宽、高是1 000 mm×80 mm×100 mm,材料是4 mm厚的KS 700钢。
在台架基板上方支架中部安装变形梳,如图2所示,在爆炸试验中,变形梳的主要作用是测量基板的变形量。试验时台架的布置如图3所示。
试验后,台架整体并未出现明显的结构损坏,测量得到的基板最大瞬态变形为89 mm。

图2 变形疏布置示意图

图3 爆炸试验台架示意图
2.2 防护组件台架爆炸有限元模型建立
针对某军用车辆底部防护组件,建立爆炸冲击台架模型如图4所示。线性强化弹塑性本构模型的材料参数如表1所示。
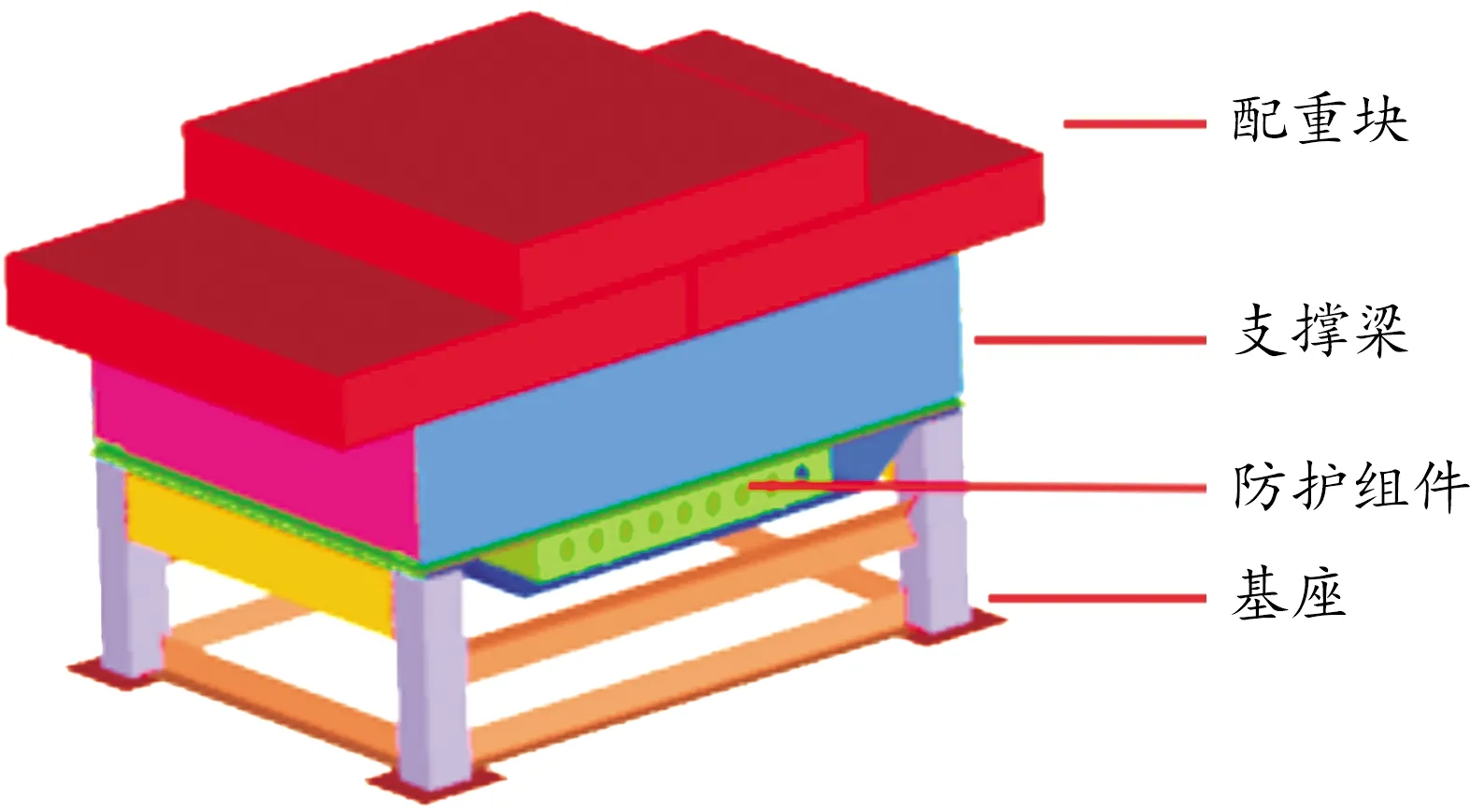
图4 爆炸冲击台架有限元模型示意图
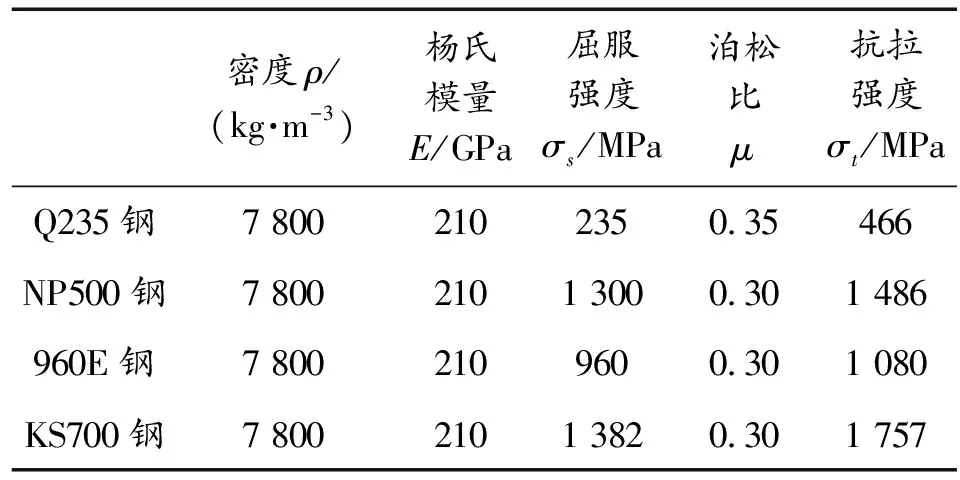
表1 本构模型材料参数Table 1 Material parameters for constitutive model
根据台架试验模型建立空气域及土壤域,建立的ALE仿真模型如图5所示。空气网格模型为2 400 mm×2 400 mm×1 800 mm的立方体,土壤网格模型为2 400 mm×2 400 mm×800 mm的立方体,网格单元尺寸为40 mm的六面体实体单元,空气网格模型下表面与土壤网格模型上表面采用共节点的方式连接。
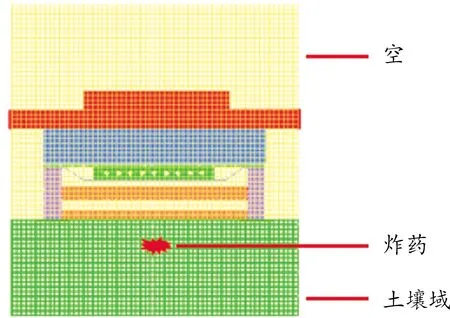
图5 ALE爆炸仿真模型示意图
2 kg当量的TNT炸药放置于台架中心正下方,采用初始体积法(Initial volume fraction geometry)对炸药定义,采用ALE-FSI的方法可以较精准地模拟地雷的爆炸对防护组件结构的加载[12]。
2.3 仿真结果分析及模型有效性验证
试验台架中用基板来模拟车辆地板,当车辆底部发生爆炸时,车辆地板会发生变形侵入到车内,挤压车内乘员的生存空间,对乘员造成伤害;与此同时,地板的垂向运动也会对乘员造成强烈的冲击,伤害乘员的下肢、盆骨、腰椎等部位[13]。因此,基板的变形和速度是影响乘员安全的2个关键因素,本文采用基板的最大瞬态变形和最大动能作为衡量底部防护组件的指标。
为确保后续工作的有效性,需要将仿真结果与试验结果进行对标,试验后基板、变形疏状态如图6;仿真分析后,基板的变形云图如图7,基板挠度时程曲线如图8,基板的最大瞬态变形为92.49 mm;基板的最大动能为16.9 kJ。仿真中基板最大瞬态变形与试验中测得的基板最大瞬态变形误差为3.92 %,在可接受的范围内。综上所述,仿真精度满足要求。

图6 试验后状态图
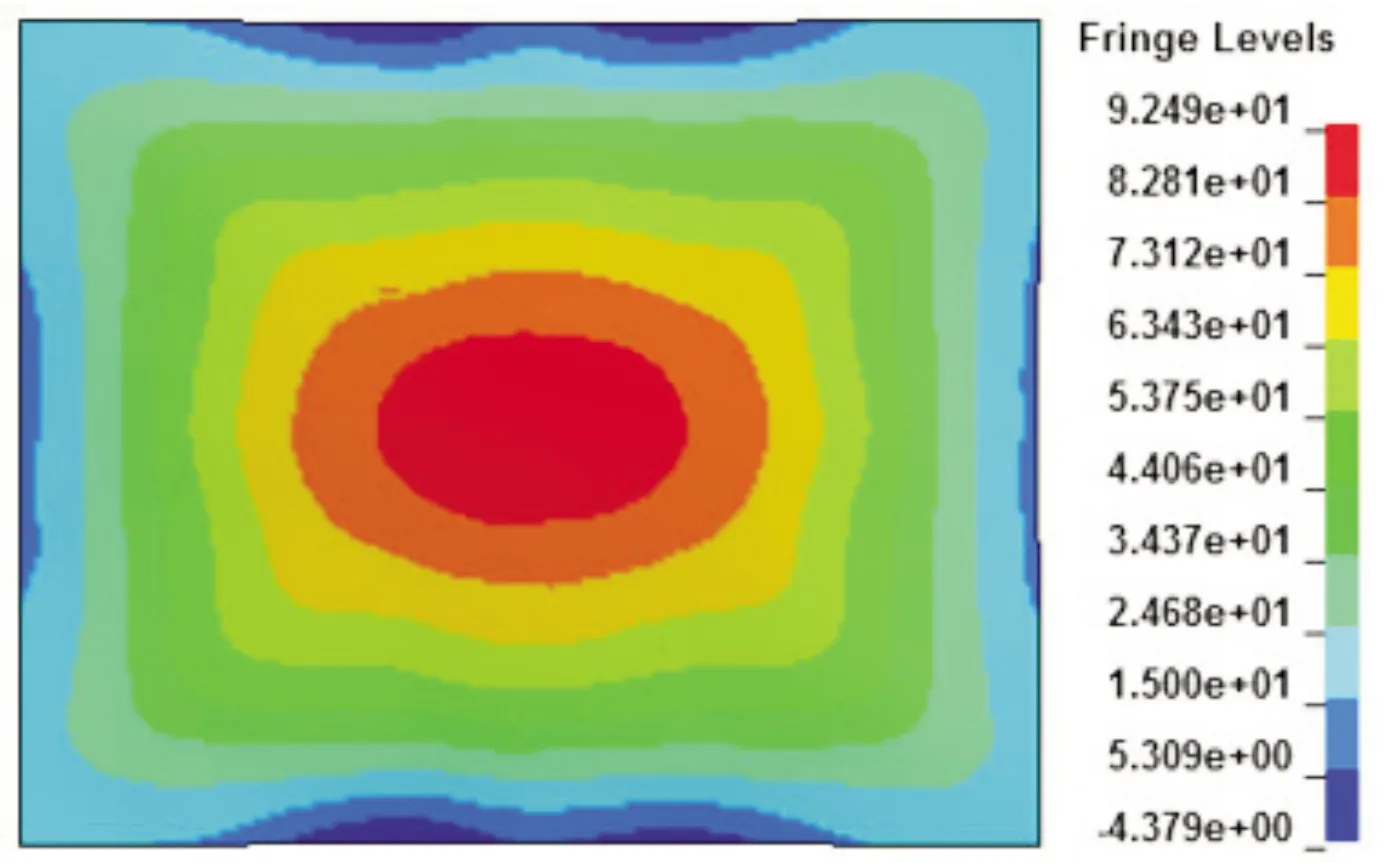
图7 基板变形云图
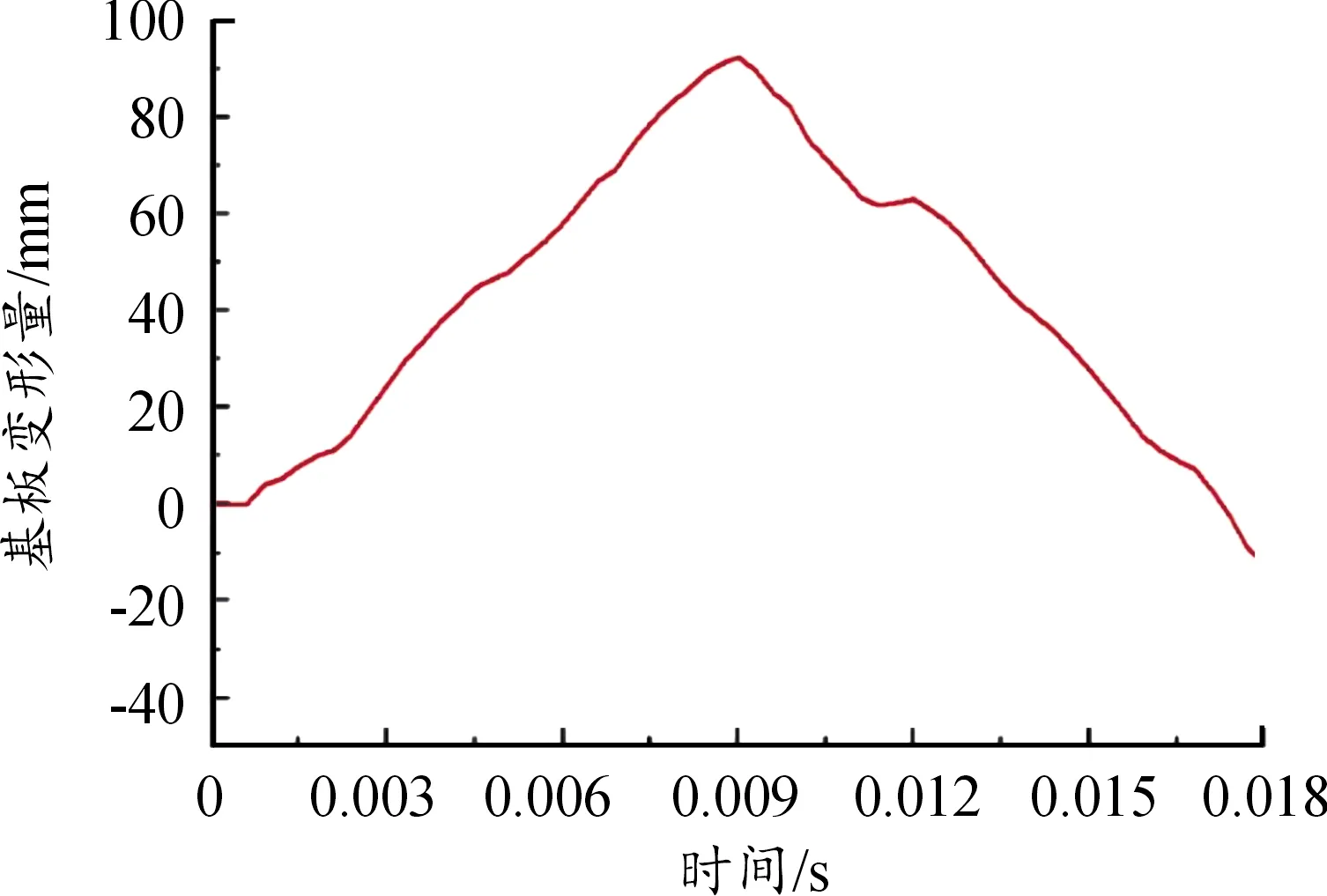
图8 基板挠度时程曲线
3 厚度梯度负泊松比结构防护组件设计
为了使组件具有更好的抗爆炸冲击的能力,在上述组件面板与背板之间放入负泊松比蜂窝芯层,如图9所示。负泊松比蜂窝夹芯材料如表2所示。

图9 负泊松比结构夹层防护组件示意图
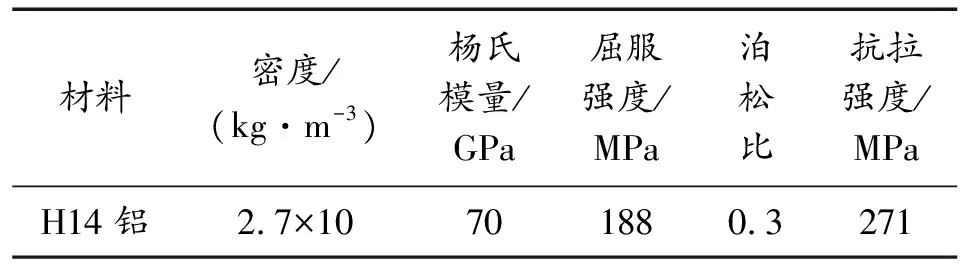
表2 负泊松比夹芯材料参数Table 2 Negative Poisson’s ratio sandwich material parameters
3.1 均质负泊松比蜂窝结构
防护组件中负泊松比芯层部分示意图及负泊松比胞元尺寸如图10所示。芯层共有3层,总质量为15.03 kg,总高度为90 mm。
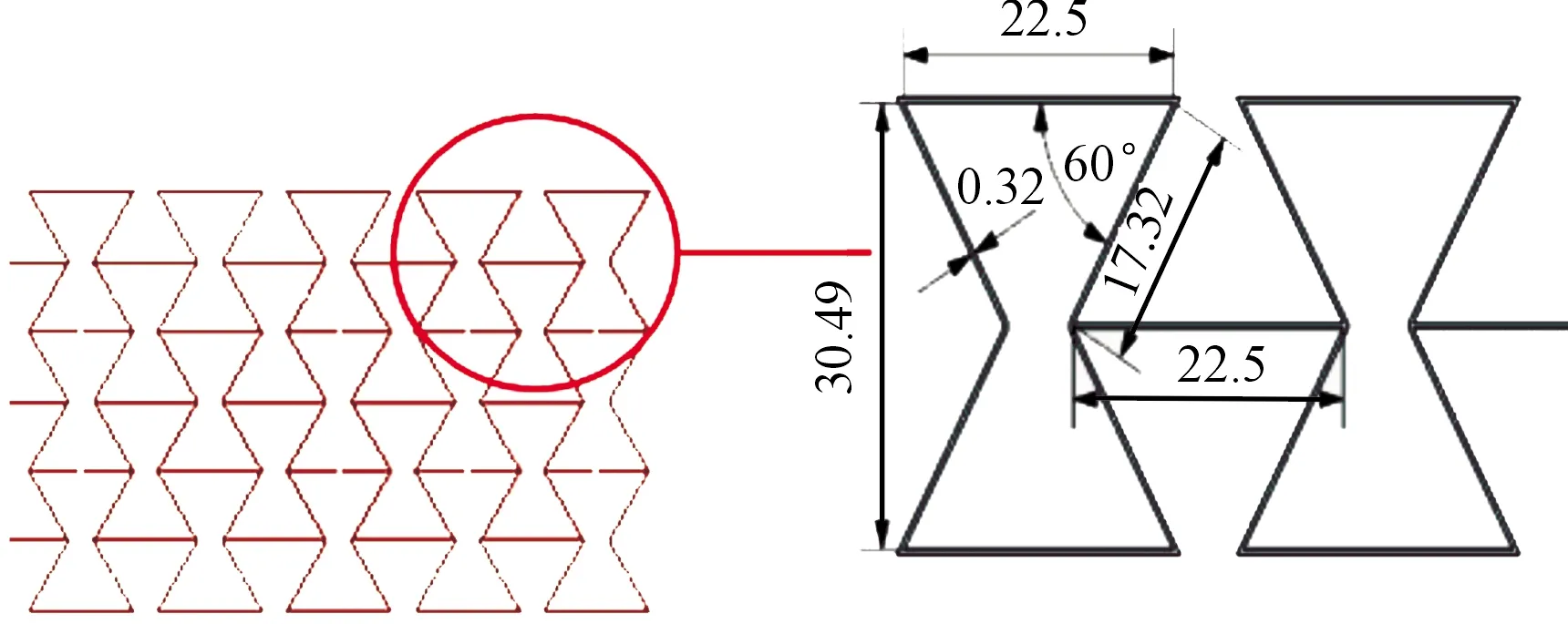
图10 负泊松比芯层示意图
3.2 厚度梯度负泊松比蜂窝芯层防护组件的爆炸仿真分析
使用均质负泊松比蜂窝材料很难达到多目标优化设计的目的[14],而具有功能梯度变化的结构相较于均质结构在抗冲击性能等方面拥有较大的优势。因此,在均质负泊松比蜂窝芯层上引入厚度梯度,研究厚度梯度型负泊松比蜂窝芯层的防护组件对基板最大瞬态变形及基板最大动能的影响。
3.2.1不同工况设置
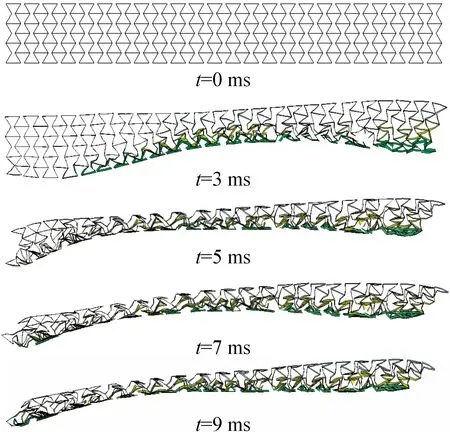
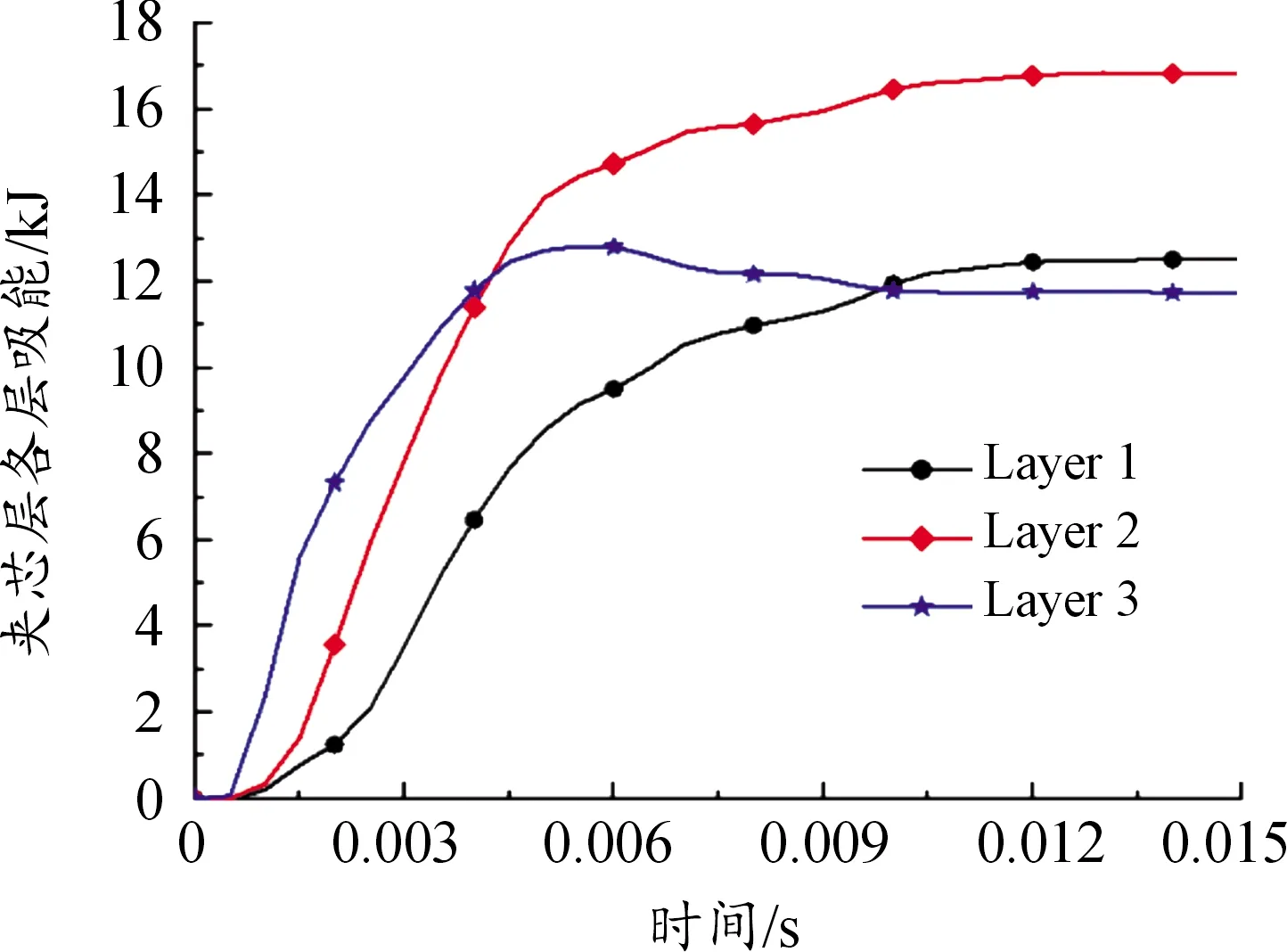
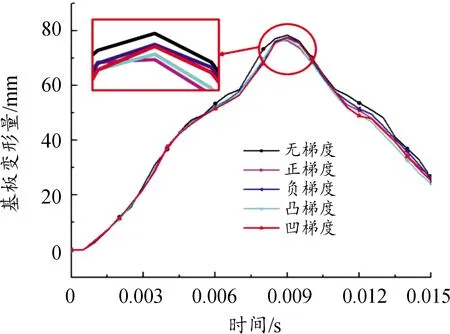
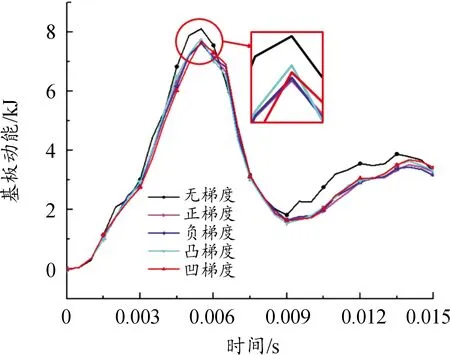
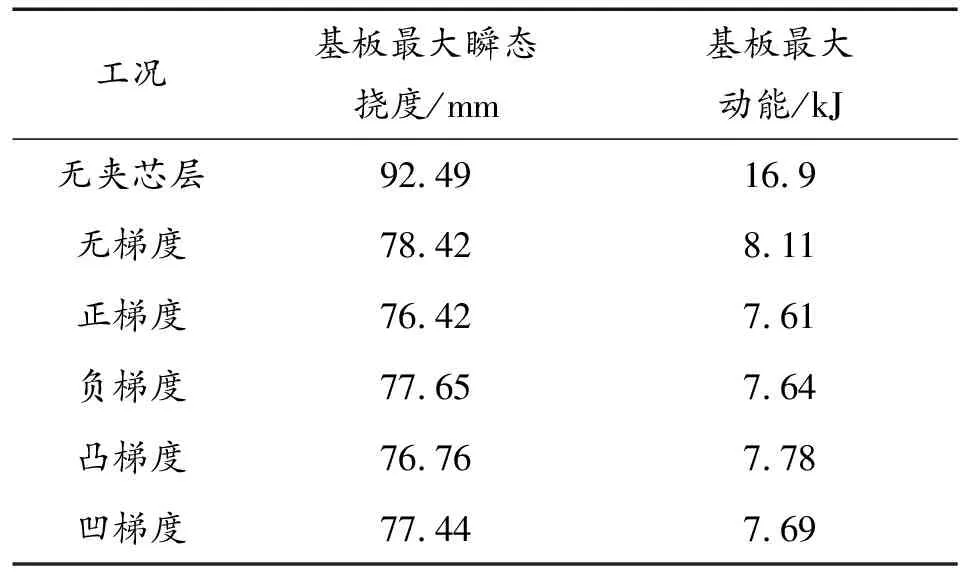
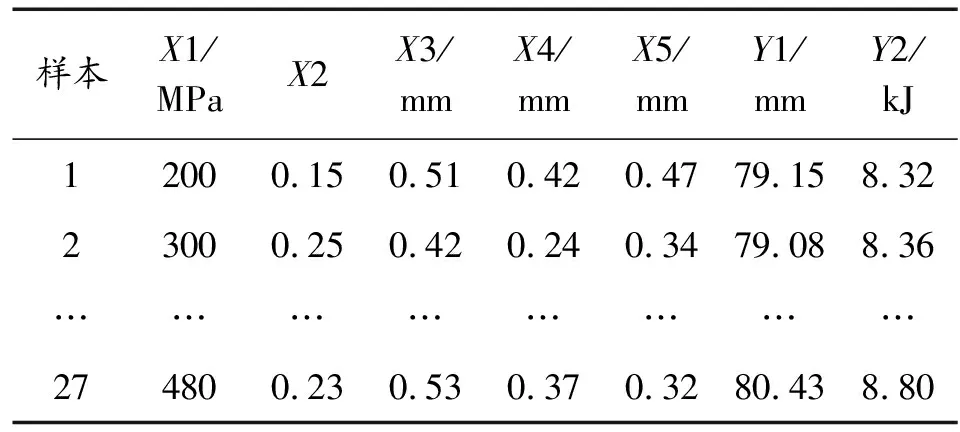
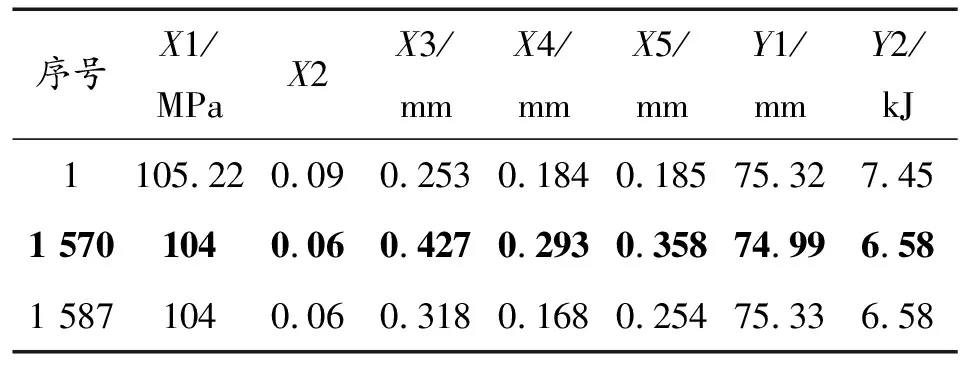
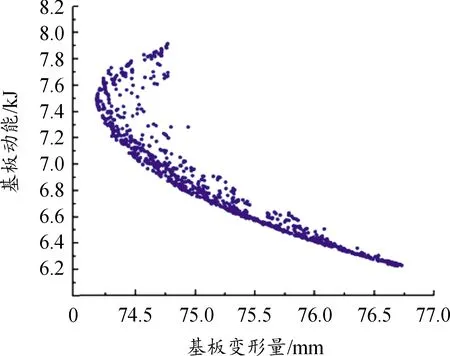
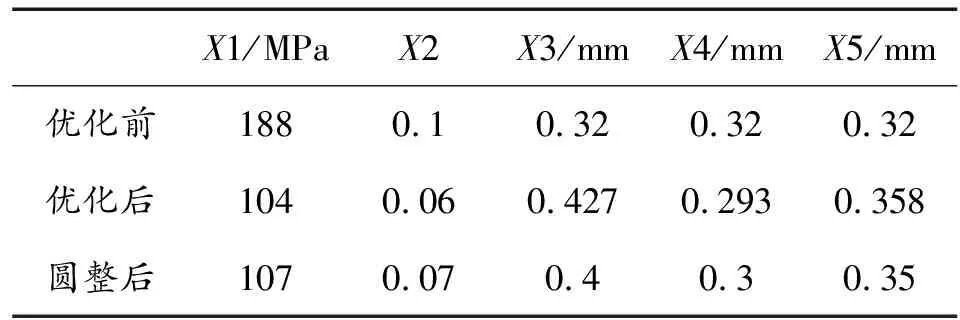
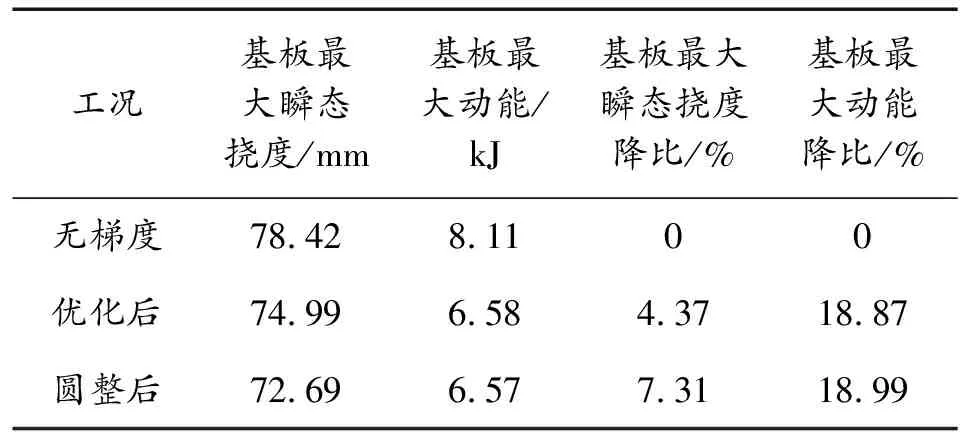
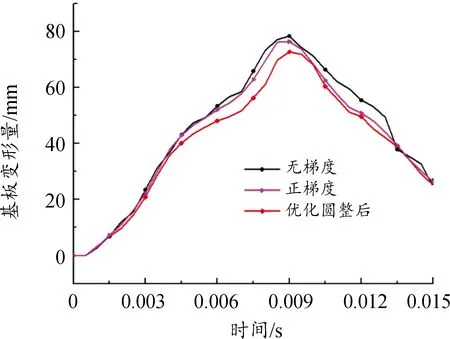
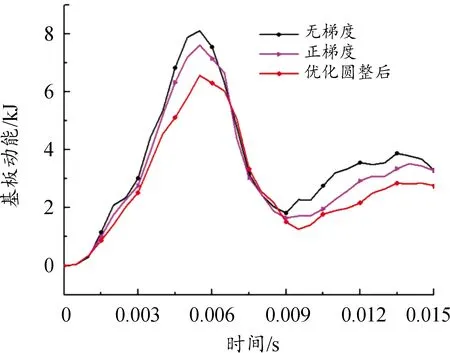
针对前文中均质负泊松比芯层,将芯层部分分为3层,从背爆侧开始,分别为第1、2、3层,各层壁度依次为t1、t2、t3,如图11所示。在保证芯层总质量为15.03 kg不变的条件下,对芯层各层厚度设置5种不同厚度梯度工况,当t1=t2=t3时,为均质结构,无梯度;当t1>t2>t3时,为正梯度;当t1 图11 负泊松比芯层各层壁厚示意图 表3 不同工况尺寸Table 3 SizeTable for different working conditions 3.2.2不同厚度梯度型负泊松比蜂窝芯层组件爆炸仿真分析 对上述不同厚度梯度型负泊松比蜂窝芯层的防护组件进行爆炸仿真分析,以正厚度梯度负泊松比芯层为例进行仿真分析描述,图12为正厚度梯度负泊松比二分之一芯层爆炸仿真图;图13为夹芯层各层吸能时程曲线;图14、图15为各工况基板响应曲线。 图12 夹芯层爆炸仿真效果图 结合图12、图15,爆炸产生的冲击波在0.05 ms时作用到防护组件上;在0.05~5 ms,基板的挠度及基板动能一直增加,组件的夹芯层部分收缩吸能,各层吸收的能量也一直增加,其中,第三夹芯层吸收的能量最多,爆炸发生后5 ms,基板的动能达到最大,第三夹芯层吸收的能量也达到最大值,基板挠度及第一、二夹芯层吸能继续增大;在爆炸发生后5~9 ms,回弹力大于冲击力,动能逐渐减少,基板在惯性作用下继续向上做垂向运动,挠度持续增加,组件夹芯层部分继续收缩吸能且第二夹芯层吸收的能量高于第一、三两层,在第9 ms时,基板的中心挠度达到最大值,夹芯层部分的总吸能也达到最大值;之后,基板动能出现小幅度回弹,基板挠度逐渐降低。 图13 正厚度梯度夹芯层各层吸能时程曲线 图14 各工况基板挠度时程曲线 图15 各工况基板动能时程曲线 在爆炸发生后,厚度梯度芯层的动态响应随夹层厚度的变化而变化,厚度梯度型蜂窝芯层相比于均质蜂窝,各层在不同时间段内充分发挥各自的吸能作用。由表4可知,加入负泊松比芯层之后的防护组件,防护性能明显提升;在防护组件芯层质量保持15.03 kg不变的条件下,4种不同厚度梯度负泊松比蜂窝芯层的防护组件得到的基板挠度及基板动能都小于均质负泊松比蜂窝芯层的防护组件,其中,正厚度梯度型负泊松比蜂窝芯层的防护组件相较于均质负泊松比蜂窝芯层的组件,基板最大瞬态变形及基板动能分别降低了2.55%和6.17%。因此,厚度梯度型负泊松比蜂窝芯层防护组件的防护性能优于均质负泊松比蜂窝的组件,而且,将较薄的夹芯层放置在迎爆面时的防护效果较好。 表4 各工况爆炸仿真结果Table 4 Simulation results of explosion under different working condition 如前述内容所述,在均质负泊松蜂窝芯层上引入厚度梯度,会增加防护组件的防护性能,因此,针对前文中的均质负泊松比蜂窝芯层,进行材料结构多目标优化设计,选择最合适的材料与结构相匹配的方案,提高防护组件的抗爆炸冲击性能。 负泊松比材料使用的是铝合金材料,在众多铝合金材料牌号中,各牌号铝合金材料的力学性能参数是不一样的,即便是同种牌号的铝合金材料,当生产工艺不同时,得到的铝合金材料的力学性能参数也是不一样的。屈服强度就是金属材料发生屈服现象时的屈服极限,当大于此极限的外力作用下,就会发生永久变形;失效应变是材料相对于时间应变的变化,对材料的性能影响很大。所以,在研究中,把铝合金材料中的屈服强度及失效应变2个参数设为变量是可行的。设计变量参数如下: X1为负泊松比材料屈服强度;X2为负泊松比材料失效应变;X3为芯层第1层厚度;X4为芯层第2层厚度;X5为芯层第3层厚度;多目标优化设计数学模型如下式: MinF(x)={Fd(x),FE(x)} (1) 式中:Fd(x)为基板的最大瞬态变形;FE(x)为基板的最大动能。 试验设计(design of experiments,DOE)是各参数与目标函数之间的关系的一种科学方法[15]。本次研究中共设计27组设计变量的样本点,然后对采样的27组样本进行仿真计算,提取每个样本点计算结果中的基板最大瞬态变形Y1、基板最大动能Y2,如表5所示。 表5 基于拉定超立方的设计变量取值及计算结果Table 5 Design variable values and calculation results based on Latin hypercube 代理模型是一种将试验设计与统计理论相结合的方法[16]。Kriging代理模型通常使用复相关系数R2进行精度检验,R2公式为: (2) 2个响应的计算仿真值与代理模型预测值如图16所示。 在拉丁超立方采样所得的设计变量与目标响应结果的基础上,采用近似模型技术已经构建5个设计变量与2个目标响应之间高精度的代理模型,经过NSGA-Ⅱ多目标进化算法完成50次迭代后得到1 587组pareto解,见表6。帕累托前沿如图17所示。 根据对组件防护能力的权重,选取表6中第1 570组为最优解。第1 570组Pareto解对应的变量结果为:X1=104 MPa;X2=0.06;X3=0.427 mm;X4=0.293 mm;X5=0.358。仿真得到的基板最大瞬态变形为74.99 mm,基板最大动能为6.58 kJ。 图16 仿真值与Kriging预测值曲线 表6 Pareto解集Table 6 Pareto solution set 图17 帕累托前沿曲线 由于厚度梯度负泊松比蜂窝芯层的防护组件在运用到工程实际的过程中,在确定其材料参数及夹芯层各层厚度时,需要考虑到实际材料的力学性能参数及实际材料的厚度与尺寸,因此对所得的最优设计参数进行圆整化处理。刘春梅[17]通过改变铝合金材料形成成品之前的退火温度发现,在退火温度为420 ℃时,3003铝合金的屈服强度和失效应变分别为107.85 MPa、0.073,与优化结果比较接近,可以采用。 综上,得到的厚度梯度型负泊松比蜂窝芯层的材料、尺寸参数的取值如表7所示。 表7 参数变量取值Table 9 Parameter variable value 将圆整后的设计变量参数值代入到模型中进行仿真计算,得到的基板最大变形为72.69 mm,基板最大动能为6.57 kJ,与优化结果的误差分别为3.07 %、0.15 %,误差在可接受的范围内。 表8为不同工况下基板的响应,其中,基板最大瞬态挠度降比与基板最大动能降比都是对比均质负泊松比芯层;图18、图19为不同工况下基板挠度时程曲线和动能时程曲线。 表8 不同工况基板响应Table 8 Substrate response under different working conditions 图18 基板挠度时程曲线 图19 基板动能时程曲线 最终,在考虑到工程实际圆整后的优化结果为夹芯层t1、t2、t3的厚度分别是0.4 mm、0.3 mm、0.35 mm,最终优化圆整的结果相较于均质负泊松比蜂窝芯层,基板的最大瞬态变形降低了7.31%,基板的最大动能降低了18.99%。 本研究建立了某防护组件模型,基于均质负泊松比芯层,提出几种厚度梯度型负泊松比芯层方案,并对其开展了对比研究;通过进行材料结构一体化多目标优化设计,获得较优的芯层材料与各层壁厚相匹配的结果。主要结论如下: 1) 基于ALE算法和有限元相结合建立的仿真模型,可以有效地模拟爆炸台架试验,仿真精度较高。 2) 在无芯层防护组件中加入负泊松比芯层后,可以有效地提升防护组件的防护性能。 3) 在控制质量为15.03 kg的条件下,厚度梯度型负泊松比芯层的防护组件的防护性能高于均质负泊松比芯层的防护组件,其中,正厚度梯度型负泊松比芯层的防护性能最好。 4) 多目标优化后得到的厚度梯度型负泊松比芯层的防护组件,达到了芯层材料与各层壁厚的较优匹配效果,相较于均质负泊松比芯层的防护组件,基板的最大瞬态挠度降低了7.31%,基板的最大动能降低了18.99%。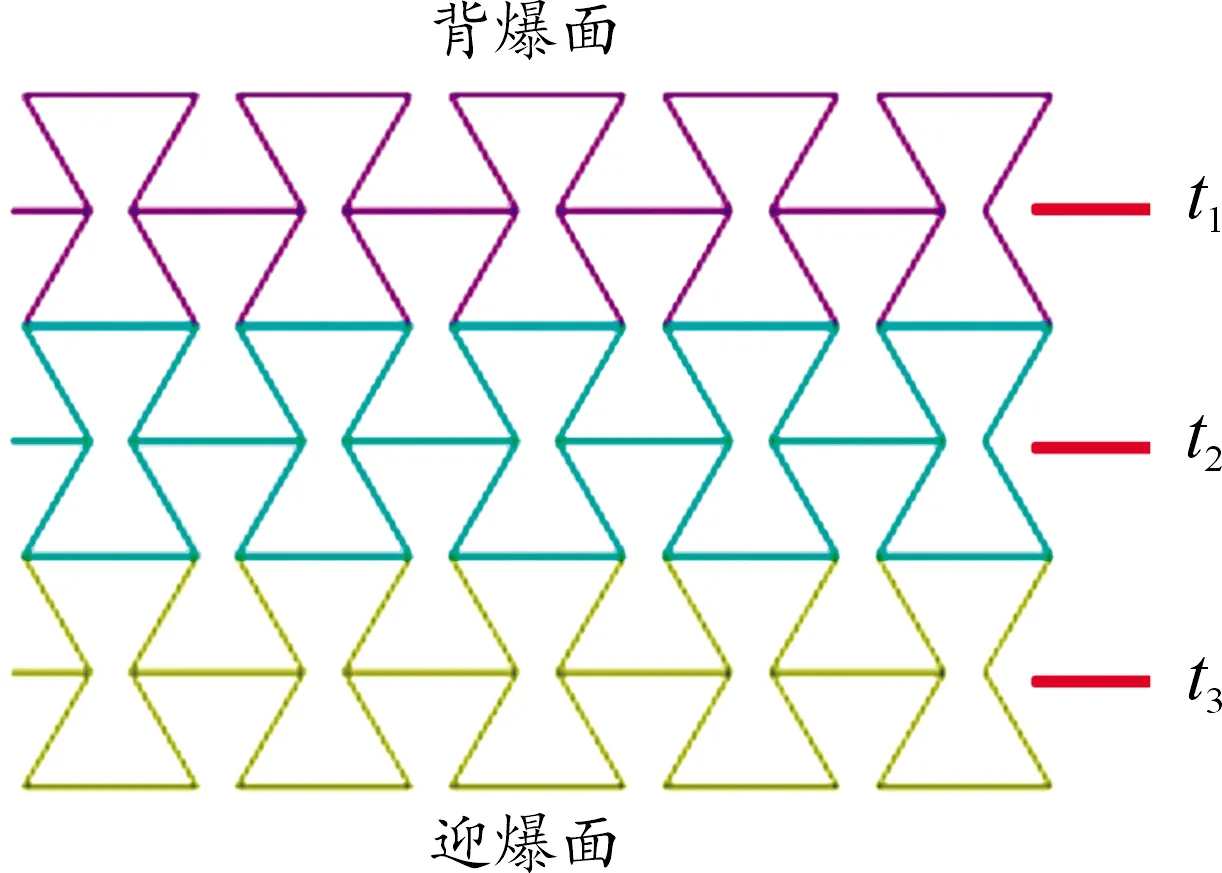
4 厚度梯度负泊松比蜂窝芯层材料结构一体化优化设计
4.1 优化模型建立
4.2 试验设计
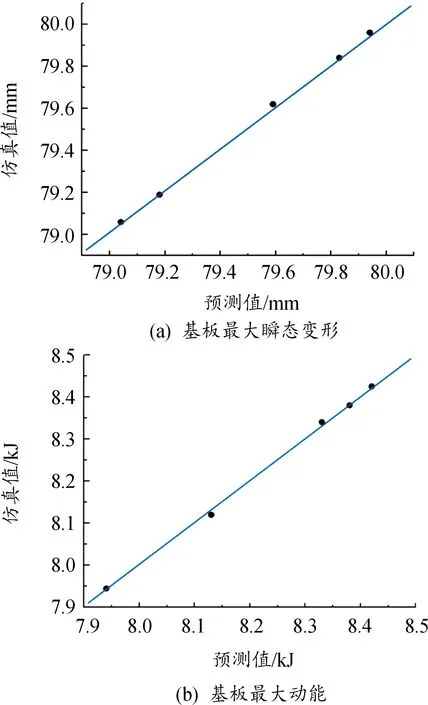
4.3 代理模型的建立
4.4 寻优计算
4.5 优化结果验证
5 结论

