基于四线性平行因子的机械故障盲分离方法

朱亚静，李志农，，杨晓飞，李泽东，陶俊勇

(1.南昌航空大学 无损检测教育部重点实验室，南昌 330063;2.国防科学技术大学 装备综合保障技术重点实验室，长沙 410073)

1 引言

盲分离(blind source separation，BSS)可以在源信号和信号传输的混合通道等先验知识未知的情况下分离观测信号获取有用源信号。传统机械故障盲分离方法中常采用二阶统计量的方法进行混合矩阵和源信号的估计，例如，刘欢[1]在风力机主轴承的故障诊断中引入二阶统计量BSS算法该应用取得了良好的效果。文献[2]中将EMD和ICA相结合用于去除风电机机组的强干扰信息，分离混合信号得到源信号估计。但是这些传统的源数估计方法和故障源信号识别方法均属于二维数据处理方法，采用矩阵分解，需要添加一些约束或者限制条件(比如恒模约束以及正交约束)才能使其分解具有唯一性。实际应用中并不能满足这些苛刻的约束条件，因此需要研究新的方法来解决这些不足。

PARAFA因分解具有唯一性而备受关注。PARAFAC概念开始于心理学领域，后来快速的在许多领域得到发展和应用[3]。尤其，PARAFAC能够充分利用信号的代数性质使其在通讯和机械故障信号处理等领域发展迅速，其主要通过多维数据的拟合迭代求得各种参数估计[4-5]。杨若男等[6]为了解决SIMO-OFDM系统下的信道估计和符号检测问题，建立了PARAFAC模型，利用此模型中的行满秩特性，并且结合奇异值分解，提出了一种联合盲估计的求解方法，成功减少了计算的复杂度，同时也避免了性能下降的问题。但是实际的应用中，使用现有的三线性平行因子方法实现机械故障的诊断时，只能对采集信号的传感器数目，振动信号的分段数以及每个数据段包含的数据点数信息进行建模，振动信号中的时间序列信息被完全忽略，振动信号包含的信息不完整，所以有必要将三维平行因子方法扩展至四维。目前，三线性平行因子向四线性平行因子的扩展有许多的进展。Shang F[7]在三线性平行因子模型的基础上，加入一个维度使其成为四线性平行因子模型，进行四维数据的获取与分析，结果表明四线性平行因子比三线性平行因子效果更好。文献[8]中通过使用模拟和实验数据集比较PARAFAC和四线性PARAFAC，结果表明四线性PARAFAC可以从数据中提取更多的信息，而且证实了与三线性平行因子分解算法相比四线性平行因子具有更高的参数估计精度。随着研究的深入诸多文献均表明四线性PARAFAC比三线性PARAFAC有更好的应用价值。

基于以上理念，本文中提出了一种基于四线性平行因子的机械故障源盲分离方法，四线性盲分离模型相比于传统的盲分离优势明显，主要表现在：分解在宽松条件下具有唯一性，可扩展范围广，利用数学分离的思想代替传统的信号分离的思想。该方法相比于在传统平行因子分解算法主要优势主要表现在：① 在三维的基础引入第四维解决振动信号时序信息被忽略的问题，数据包容量大，建模时包含的信息更加完整；② 在宽松条件下分解具有唯一性，可扩展范围广。利用四线性交替最小二乘进行迭代拟合，收敛更加平稳，预测能力更强。

2 四线性平行因子理论基础

四维矩阵X∈CI×J×K×L的四线性成分模型分解示意图如图1。

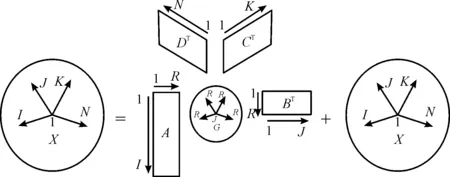
图1 四线性成分模型分解直观分解示意图Fig.1 Intuitive decomposition diagram of quadrilinear component model decomposition

其中，X是一个四维矩阵，将X分解为大小分别为I×R，J×R，K×R，N×R的相关矩阵A，B，C，D。G是一个四维核对角矩阵，维数为I×J×K×N，并且超对角元素为1，其他元素为0。E为一个I×J×K×N四维残差矩阵。

矩阵X∈CI×J×K×N的四线性成分模型标量形式通常可以表示为：

(1)

其中，A∈CI×R，B∈CJ×R，C∈CK×R，D∈CN×R分别为四线性成分模型的4个承载矩阵。k=1，2,…,K，n=1，2,…,N，i=1，2,…,I，j=1，2,…,J，E∈CI×J×K×N为四维残差矩阵。

四线性平行因子模型是将四线性成分模型中的四维矩阵X铺展成二维矩阵形式，沿4个方向进行交替分解得到，有4种表述形式：

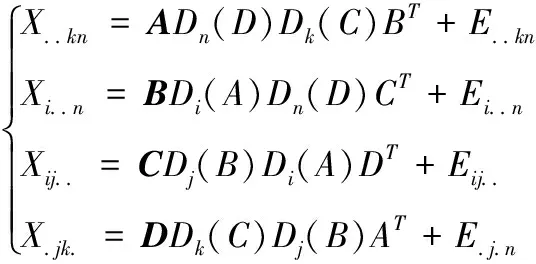
(2)

其中，Di(A)，Dj(B)，Dk(C)，Dn(D)为对角化算子，Di(A)表示矩阵其余的位置均为零，主对角线元素以矩阵A的第i行作为元素的新生成矩阵。其他对角化算子表示的含义与Di(A)表示的含义相似。

3 四线性平行因子盲分离模型

线性瞬时混叠模型可以表示为：

X(t)=Α(t)·S(t)+E(t)

(3)

式中：X(t)=[x1(t)，x2(t)，…,xN(t)]T为N维观测信号；S(t)=[s1(t)，s2(t)，…，sM(t)]T为M个源信号；Α(t)是维度为N×M的混合矩阵；E(t)是噪声信号。假定一个时间段内每个观测信号的数据点为L个(共N个传感器)，将观测信号中心化处理，接着将处理后的观测信号平均截成不会重复的数据段J个，每一个数据段里面含有的数据点数为L/J个，令L/J等于K。采样时间为t，每一段数据对应的采集时间为h，则共分为t/h个时间段记其为I。则式(3)可以表示为：

X(i，h)=A·S(i，h)+E(i，h)

(4)

计算各段时滞协方差矩阵Rk：

Rk(tk，h)=ARx(tk，h)AT

(5)

其中，k=1，2,…,K，序号tk表示t内第k个数据点，式中：

(6)

假设每个源信号均不相关，则块时滞协方差矩阵化可以化为对角矩阵，令这个对角矩阵为B，则式(5)化为

Rk(tk，h)=Adiag(B)AT

(7)

接着计算一个时间段内N个观测信号的源时滞协方差Rn：

Rn(tn，h)=ARS(tn，h)AT

(8)

式中tn表示t内第n个观测信号，式(8)中RS(tn，h)可以表示为：

(9)

将源时滞协方差矩阵化为对角矩阵，并令这个对角矩阵为C，则式(7)化为：

Rn(tn，h)=Adiag(C)AT

(10)

所有的源时滞协方差矩阵和块时滞协方差矩阵叠加为三阶张量，并且将这个三阶张量记为Rk，n：

(11)

其中，diag(A)，diag(B)，diag(C)，diag(D)是载荷矩阵A，B，C，D的对角阵。k=1，2，…，K，n=1，2，…，N。K×N个切片累积成N×J×K×I的四维形式，R为最佳组分数，则其四线性平行因子标量形式可表示为：

(12)

式中，r=1，2，…，R，并且n=1，2，…，N，j=1，2，…，J，i=1，2，…，I，k=1，2，…，K，式(12)即为四线性平行因子盲分离模型。

4 四线性平行因子的分解

kA+kB+kC+kD≥2R+3

(13)

则在宽松条件下，A，B，C，D可唯一确定，也就是X的K秩分解具有唯一可以确定，即四线性分解具有唯一性。其中，kA，kB，kC，kD分别是载荷矩阵A，B，C，D的秩，R表示四线性平行因子模型中的成分数。

四线性平行因子用四线性交替最小二乘方法(quadrilinear alternating least square，QALS)完成四线性平行因子模型的拟合迭代，其基本思路是每一步更新一个矩阵，更新办法是：对余下的矩阵，依据前一次估计的结果，利用最小二乘法来更新，该形式的更新迭代过程一致重复，直至算法收敛。相比于三线性迭代方法，该方法拟合精度更高，表现更平稳，收敛速度更快。一般来讲，迭代过程是通过初始化承载矩阵B，C，D，然后根据式(14)求出A，根据求得的A，由式(15)、式(16)、式(17)依次分别求出矩阵B，C，D。循环该过程直至算法收敛。

A=XI×JKN[(B⊙D⊙C)T]+

(14)

B=XJ×KLI[(A⊙D⊙C)T]+

(15)

C=XK×NIJ[(B⊙D⊙A)T]+

(16)

D=XN×IJK[(B⊙A⊙C)T]+

(17)

四线平行因子分析的步骤为：

1) 估计最佳组分数

2) 初始化3个载荷矩阵B，C，D

3) 由式(14)迭代计算A

4) 依据迭代计算的A由式(15)迭代计算B，依次计算C，D。

5) 重复步骤3)和4)，到收敛至满足收敛准则。

该算法可通过优化式(18)所示的迭代函数实现X的分解:

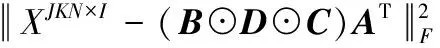
(18)

四线性平行因子迭代的停止准则是：

(19)

其中：上标符号“+”含义为Moore-Penrose伪逆；⊙代表矩阵的Khatri-Rao积；ε残余误差的平方和，m为迭代次数。一般认为ε为1×10-6，当满足式(19)就可以认为算法收敛。

5 仿真研究

模拟两组调制信号s1(t)，s2(t)来产生数据仿真说明算法有效性。信号s1(t)由基频为70 Hz，调频为30 Hz的信号和一频率为150 Hz的正弦信号叠加而成。信号s2(t)由基频为120 Hz，调频为10 Hz的信号和一频率为145 Hz的正弦信号叠加而成。

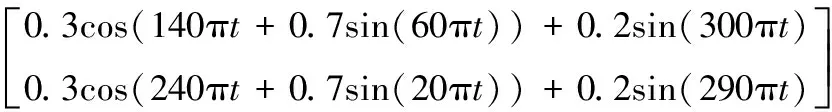
(20)

2组源信号的采样频率为Fs=3 000 Hz，采样点数为N=10 240，源信号s1(t)，s2(t)的时域波形图如图2，幅值谱图如图3。

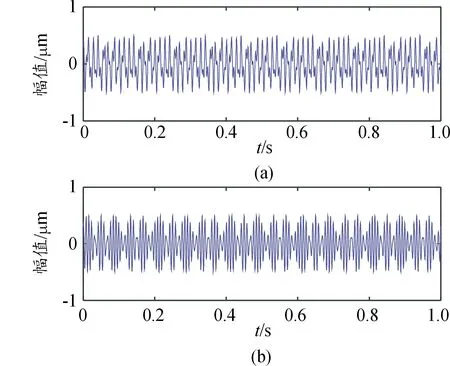
图2 源信号时域波形图Fig.2 Time domain waveform of Source signal

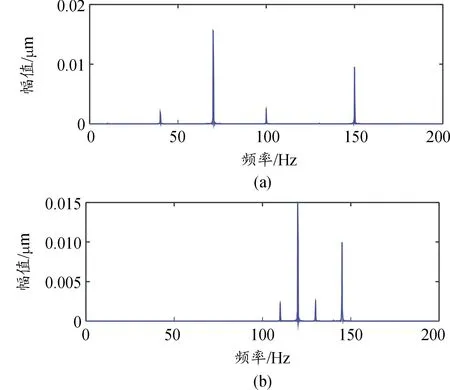
图3 源信号幅值谱图Fig.3 Amplitude spectrum of Source signal

源信号幅值谱图如图3(a)以及图3 (b)所示，图3(a)中源信号s1(t)和图3(b)源信号s2(t)的所显示的频率均为基频频率和调频频率的叠加，s1(t)其特征频率分别为40 Hz、70 Hz、100 Hz、150 Hz。s2(t)的所显示的频率也为基频频率和调频频率的叠加，其特征频率分别为120 Hz、110 Hz、130 Hz、145 Hz。

为了得到虚拟的观测信号将两路观测信号混叠为一路，这里选择一个随机混合矩阵A并且添加噪声干扰得到混叠信号时域波形图如图4，得到混叠信号幅值谱图如图5。由图4以及图5可知中两路仿真信号的源信号时域波形图完全混叠在了一起，并且两源信幅值均在混合幅值谱上显示，其特征频率分别为40 Hz、70 Hz、100 Hz、110 Hz、120 Hz、145 Hz、150 Hz，两源信号幅值谱图完全混叠，并且无法辨识两源信号的特征频率，表明两路观测信号已经完全混叠。

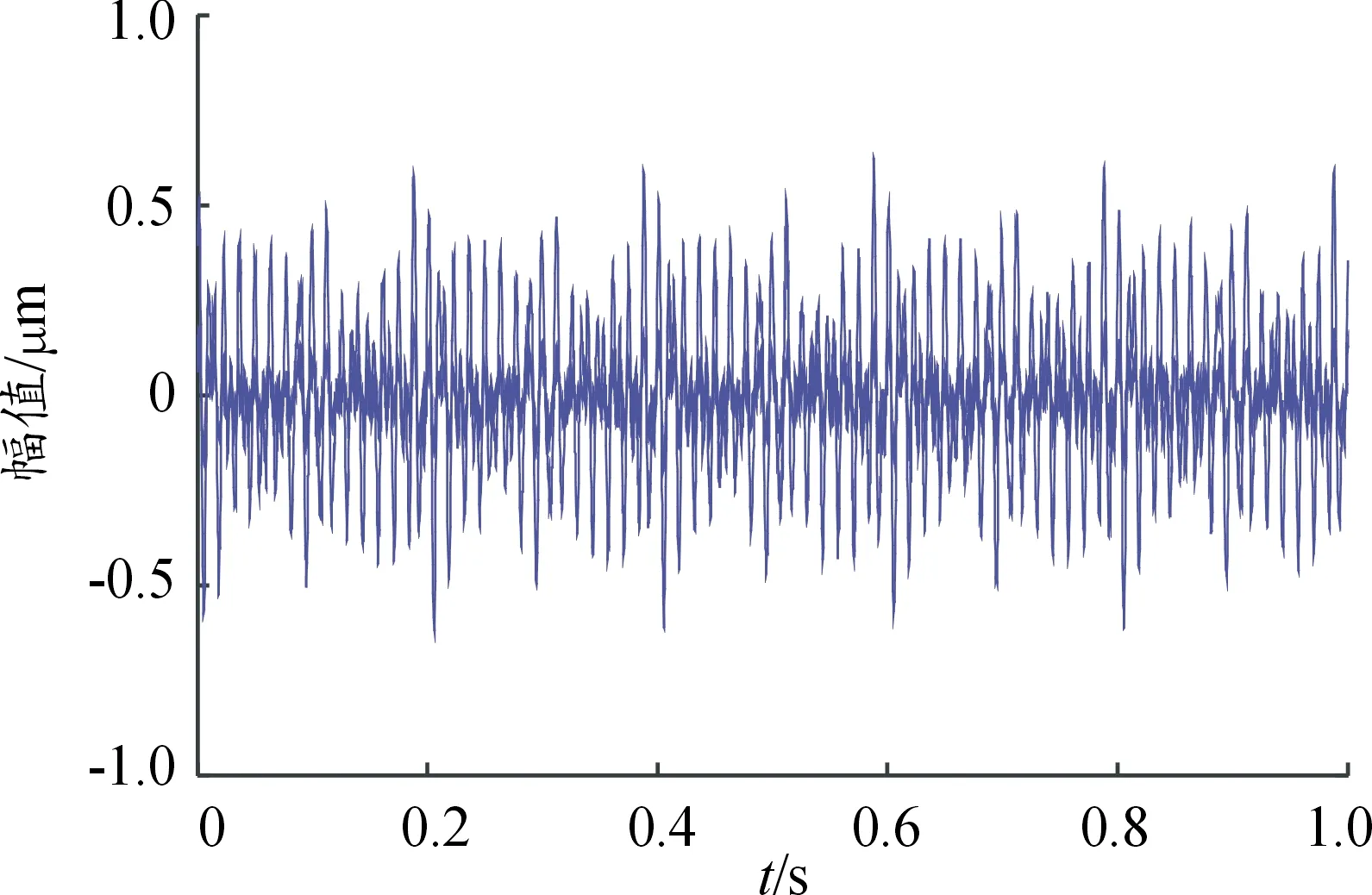
图4 混叠信号时域波形图Fig.4 Time domain waveform of aliased signal

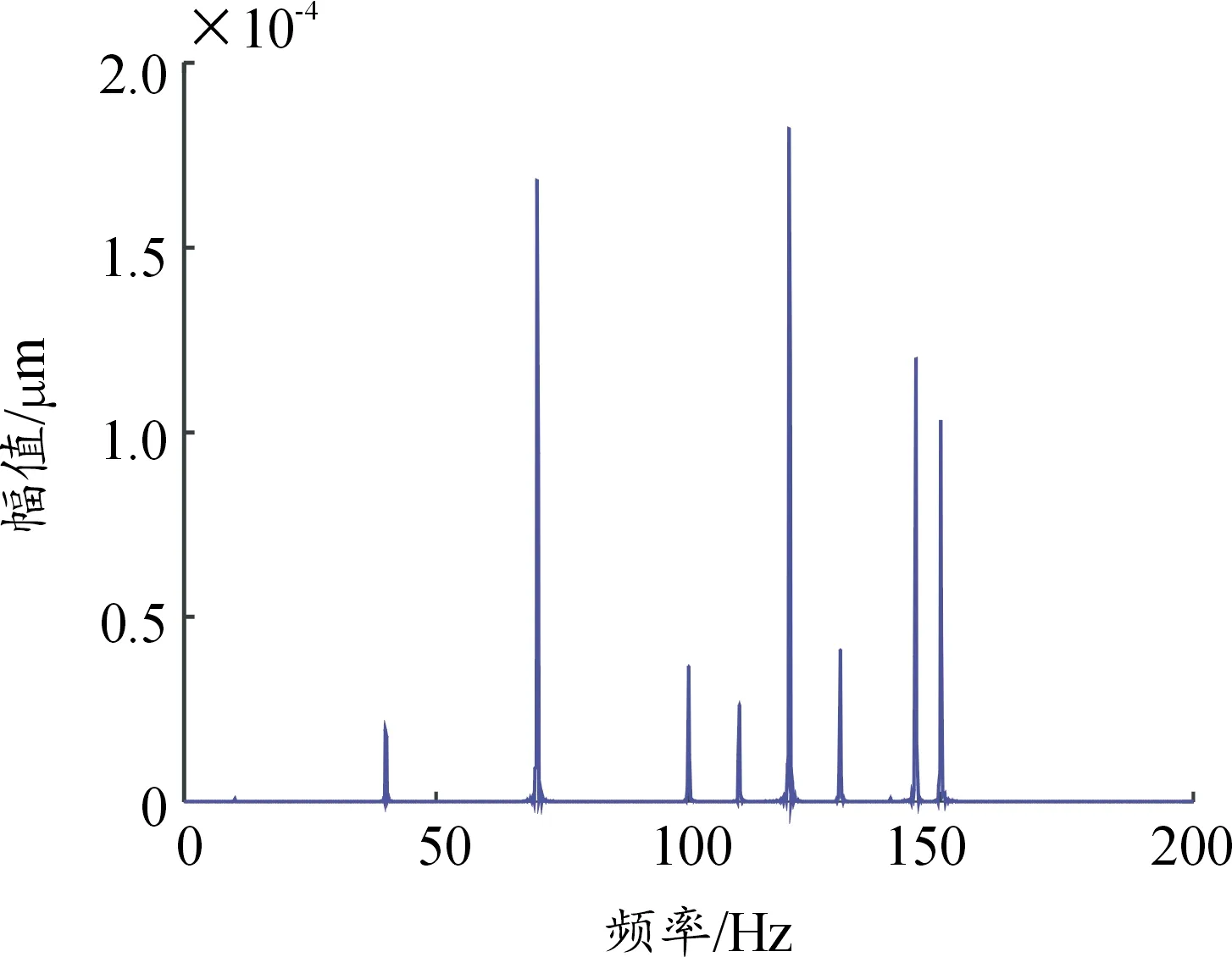
图5 混叠信号幅值谱图Fig.5 Amplitude spectrum of aliased signal

为了比较三线性和四线性的迭代平稳性和以及迭代收敛性，比较仿真信号满足三线性和四线性平行因子迭代的停止准则时三线性和四线性平行因子迭代收敛过程中迭代函数值的变化以及迭代结束时的迭代次数，比较结果如图6所示。由图6可知，迭代结束时四线性平行因子的迭代次数明显低于三线性平行因子，并且在迭代过程中，四线性迭代函数的值明显比三线性低，表明四线性相比于三线性平行因子收敛性更好，意味着四线性在的估计精度更高估计误差更小。

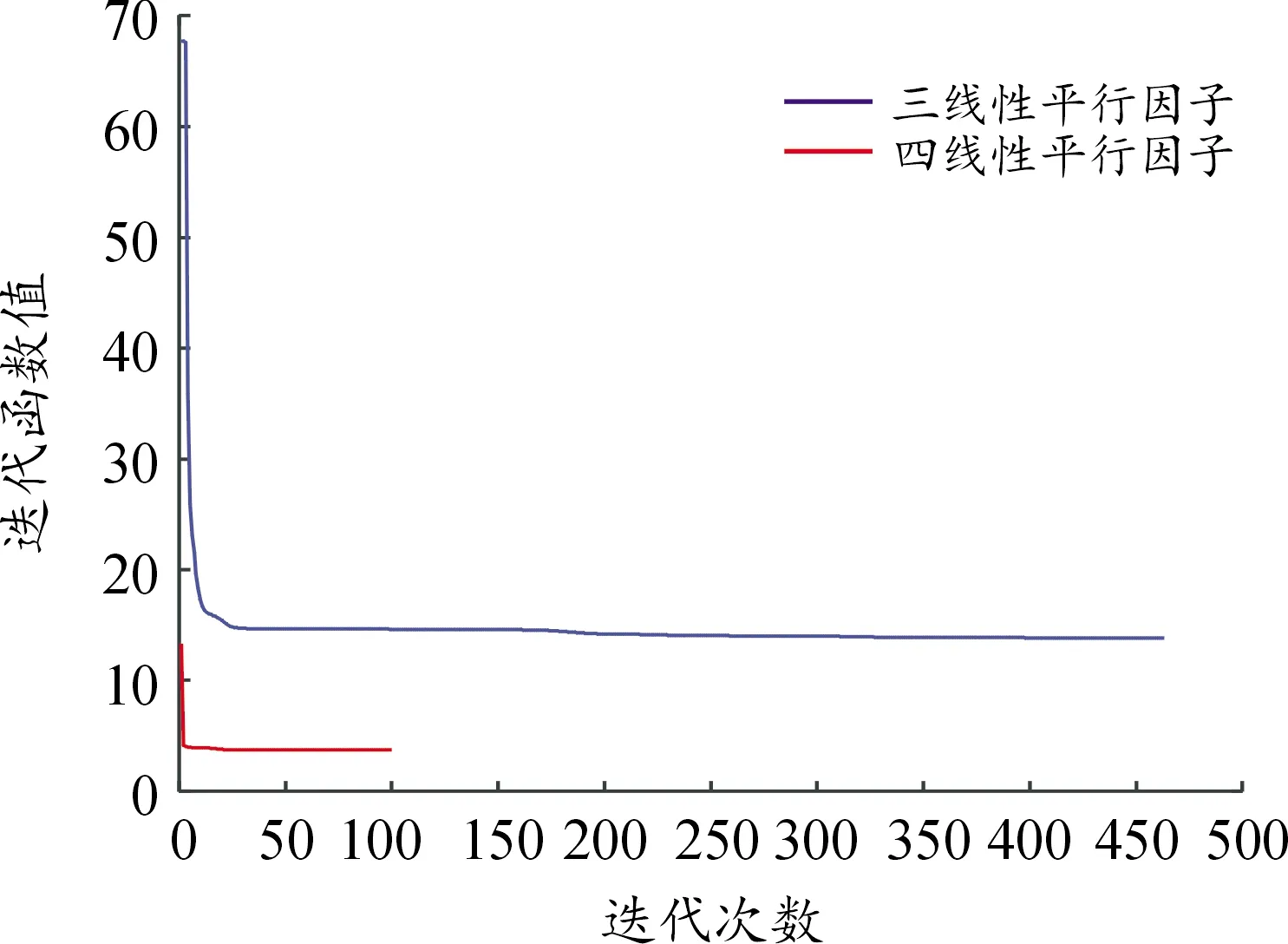
图6 迭代次数曲线Fig.6 Comparison of iteration times of different methods

用四线性平行因子盲分离方法分离混叠信号波形图得到的时域波形图，如图7(a)和图7(b)。用四线性平行因子盲分离方法分离混叠信号波形图恢复得到的幅值谱图，如图8(a)与图8(b)。用三线性平行因子分离得到的时域波形图，如图9(a)和图9(b);得到幅值谱图，如图10(a)与图10(b)。

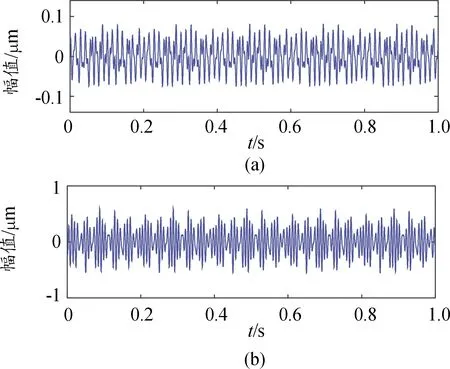
图7 恢复信号时域波形图(四线性平行因子)Fig.7 Time-domain waveform of recovered signal (quadrilinear parallel factors)

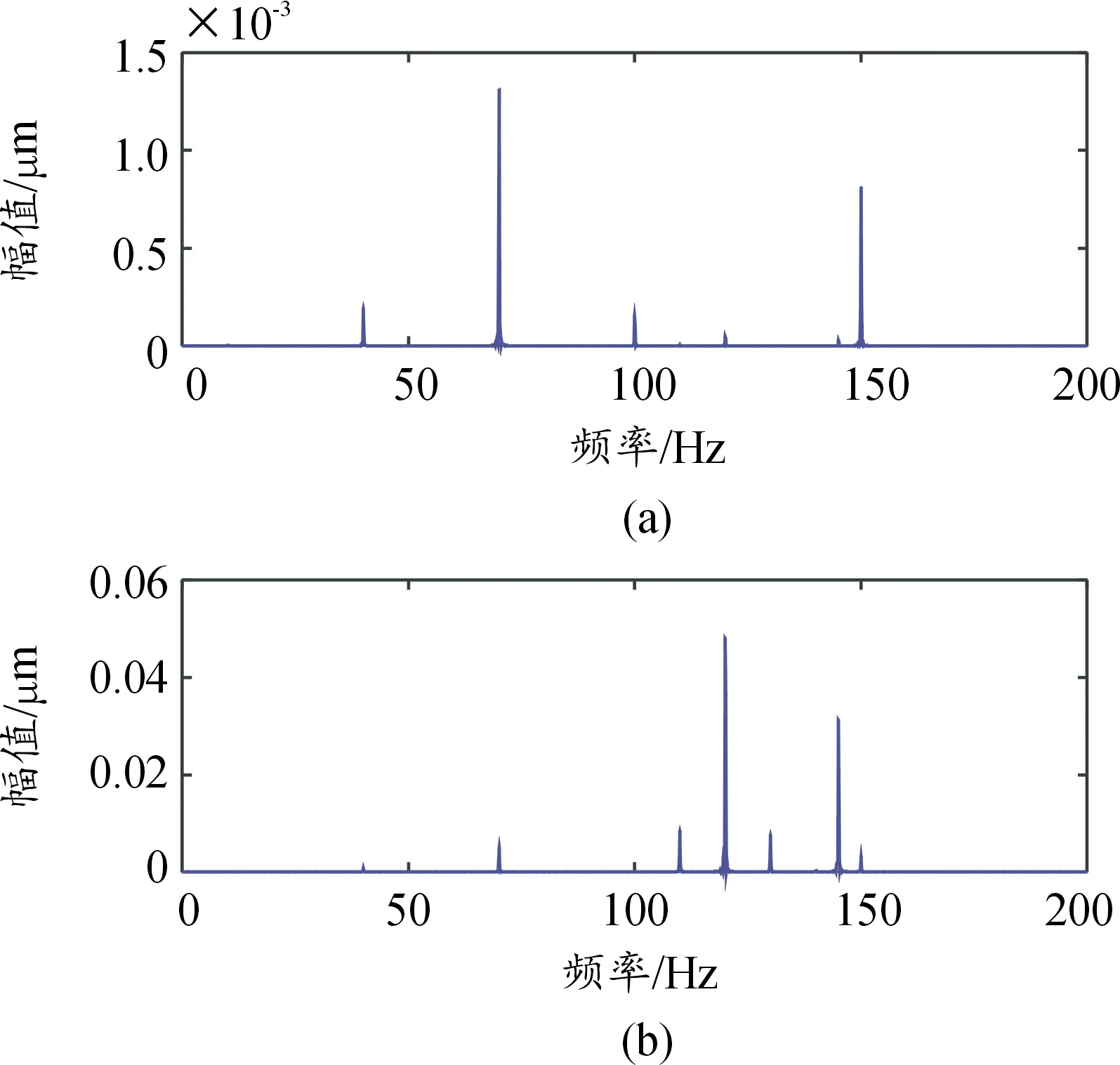
图8 恢复信号幅值谱图(四线性平行因子)Fig.8 Altitude spectrum of recovered signal (quadrilinear parallel factors)

由图8可知，用四线性平行因子盲分离方法能够分离分离混叠信号，由图7(a)可知，其主要特征频率主要为40 Hz、70 Hz、100 Hz、150 Hz，其与源信号s1(t)的特征频率基本一致，所以用四线性平行因子盲分离算法分离混叠信号其可以识别源信号s1(t)。由图8(b)可知，特征频率主要为110 Hz、120 Hz、130 Hz、145 Hz，其与源信号s2(t)的特征频率基本一致，所以用四线性平行因子盲分离算法分离混叠信号其可以识别源信号s2(t)。由图7与图2以及图4的对比(即四线性平行因子盲分离方法分离得到的时域波形图与源信号时域波形图的对比以及混叠信号时域波形图对比)可以发现四线性平行因子盲分离方法很好地分离了混叠信号，分离得到的时域波形图与源信号时域波形图相似度很高。

图9 恢复信号时域波形图(三线性平行因子)Fig.9 Time-domain waveform of recovered signal (trilinear parallel factors)

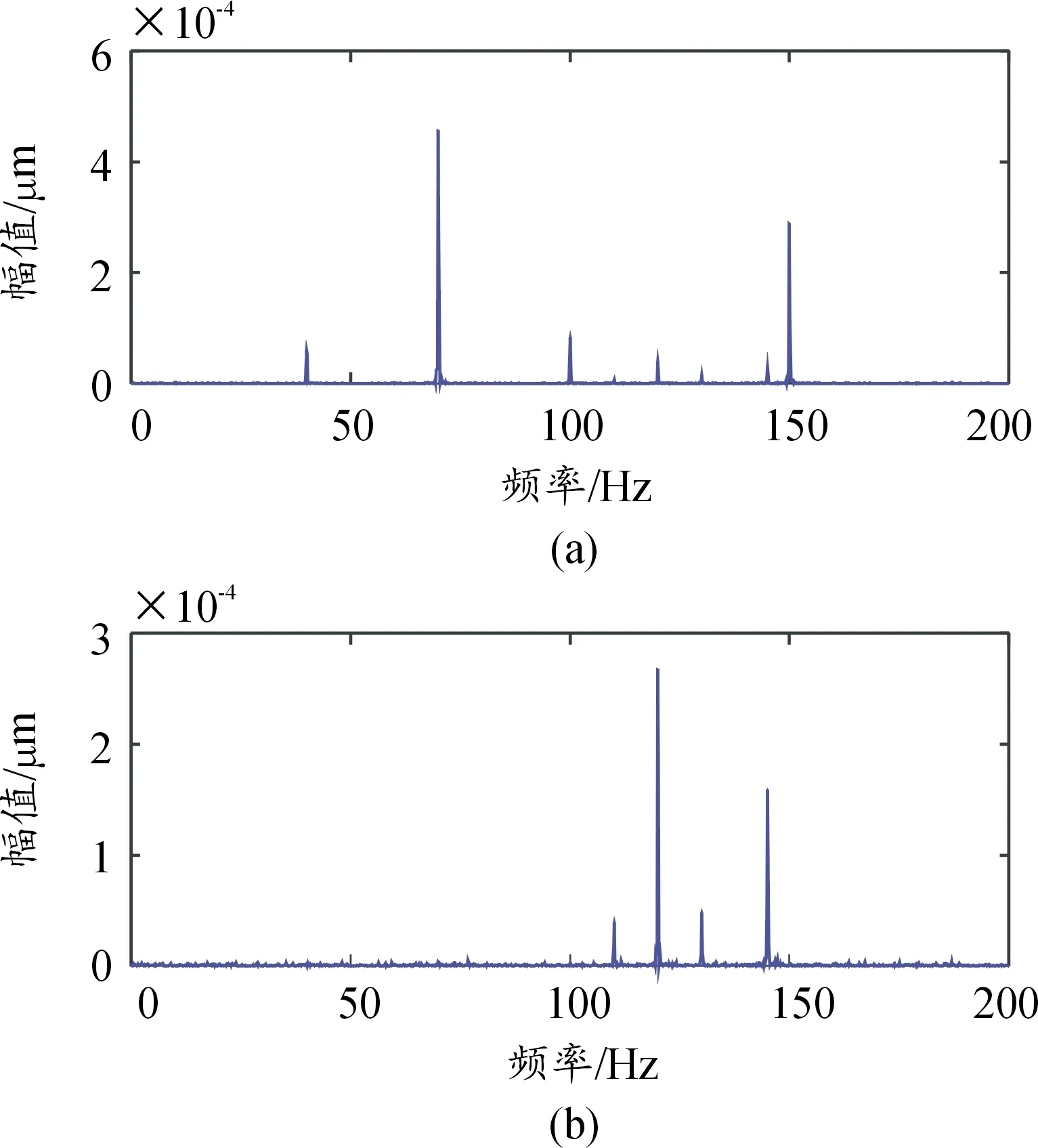
图10 恢复信号幅值谱图(三线性平行因子)Fig.10 Altitude spectrum of recovered signal (trilinear parallel factors)

由图8与图10的对比(即四线性平行因子盲分离方法分离得到的幅值谱图与三线性平行因子盲分离方法分离得到的幅值谱图对比)可知三线在分离时效果没有四线性分离效果好。由图8与图3以及图5的对比(即四线性平行因子盲分离方法分离得到的幅值谱图与源信号幅值谱图以及混叠信号幅值谱图对比)可知，四线性平行因子盲分离方法成功分离了混叠信号，并且分离得到的信号特征频率与两源信号特征频率一致，表明四线性盲分离算法可以有效地分离混合信号得到源信号。

盲源分离中通常用性能指数以及相似系数来评判分离效果的好坏，这里选择相似系数来分析评定。将混叠信号分别用三线性平行因子盲分离算法以及4-PARAFAC-BASS分离算法的分离，然后计算相似系数。式(21)是相似系数值的计算方法，式中cov(·)为方差。一般认为恢复信号与源信号越相似，则相似系数|ρij|的值越接近为1。若|ρij|值越大则表示分离效果越好，|ρij|值越小分离效果越不好。

(21)

用ρij在信噪比为20 dB时，PARAFAC-BSS分离算法与4-PARAFAC-BASS分离算法的分离性能，如表1所示。

表1 PARAFAC-BSS与4-PARAFAC-BSS的分离性能Table 1 Comparison of separation performance between PARAFAC-BSS and 4-PARAFAC-BSS

由表1可知，三线性平行因子盲源分离(PARAFAC-BSS)得到的相似系数分别是0.667 7与0.304 1与四线性平行因子盲源分离(4-PARAFAC-BSS)得到的相似系数0.932 0与0.746 4相比，四线性得到的相似系数的值更接近于1，由此可知四线性的分离效果更好。并且三线性分离中s2(t)的相似系数的值较低，分离效果很不好。综上可知，表明四线性盲分离算法可以有效地分离混合信号得到源信号。并且四线性平行因子盲分离算法得到的分离效果比三线性平行盲分离算法得到的分离效果更好，证实了所提算法的有效性。

6 实验研究

用如图11所示的实验装置，验证所提四线性平行因子盲分离算法的有效性。用电火花加工技术分别在驱动端轴承内圈中央位置以及轴承外圈中央位置加工点蚀故障，故障直径为0.007英寸，深度为0.011英寸。将加工过的故障轴承重新装入测试电机中，在电机负载为0马力的工况条件下工作，电机转速1 796 r/min，相应的转频为fr=29.17 Hz，采样频率为12 000 Hz，采样点数为24 000，轴承内圈的故障频率为104.31 Hz，轴承外圈的故障频率为143.95 Hz。当电机1单独运行时用加速度传感器采集到的振动信号数据，截取0.4 s的振动信号数据得到时域波形图如图11中(a)所示，当电机2单独运行时用加速度传感器2采集振动信号数据，截取0.4 s的振动信号数据得到时域波形图如图11中(b)所示。

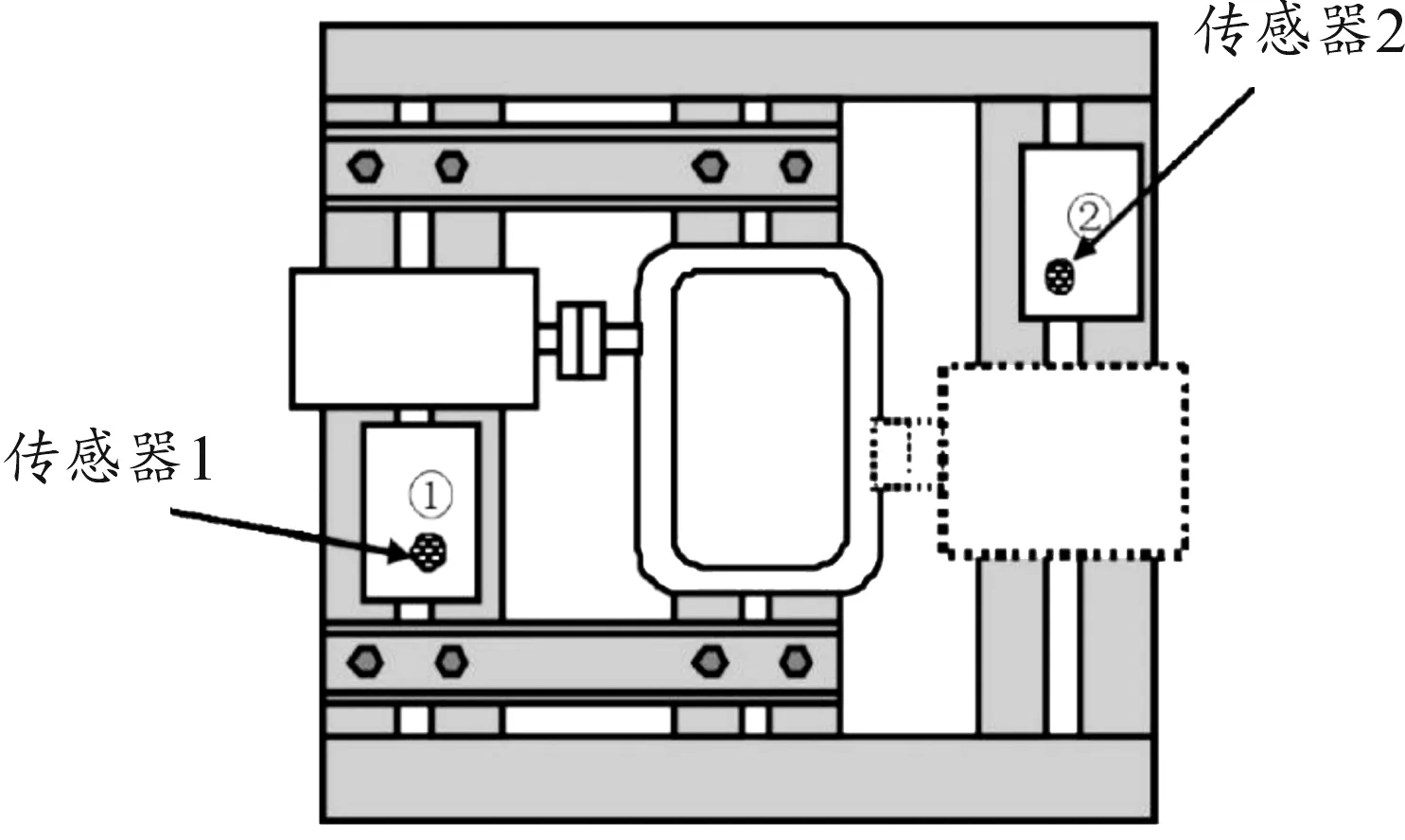
图11 实验装置示意图Fig.11 Test bed

当两电机分别单独转动时，采集数据，得到的两源信号时域波形图分别如图12(a)与图12(b)所示，幅值谱图13(a)对应特征频率为电机转频29.17 Hz，轴承故障特征频104.31 Hz，以及转频的二倍频等以及故障特征频率和转频的叠加影响频率。幅值谱图13(a)与图13(b)所示分别对应特征频率为电机转频29.17 Hz，轴承故障特征频率143.95 Hz，以及转频的二倍频等以及故障特征频率和转频的叠加影响频率。

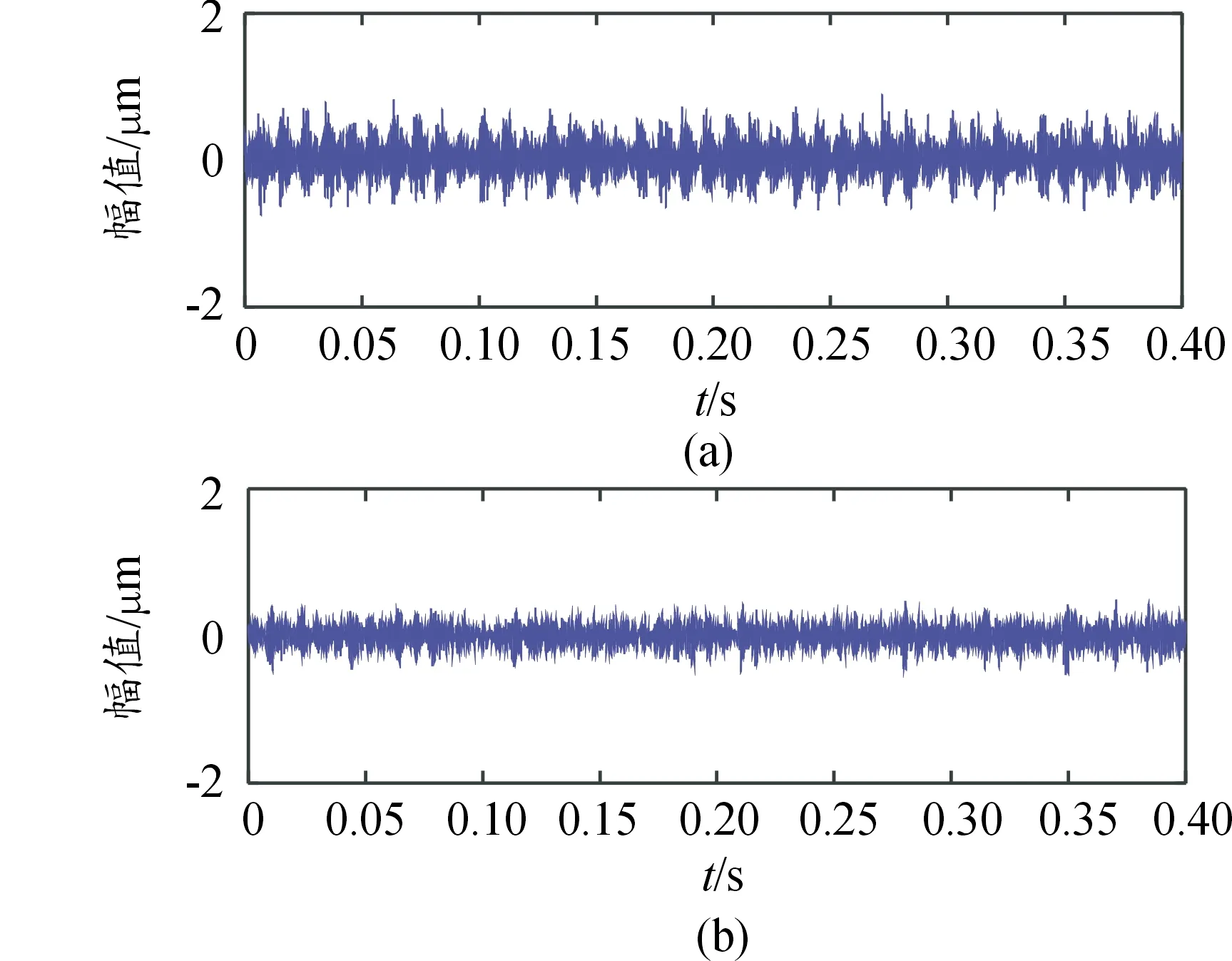
图12 源信号时域波形图Fig.12 Time-domain waveform of source signal

当电机1和电机2同时运行时得到双通道混合信号时域波形图如图14(a)与图14(b)所示，得到的幅值谱图如图15(a)与图15 (b)所示。

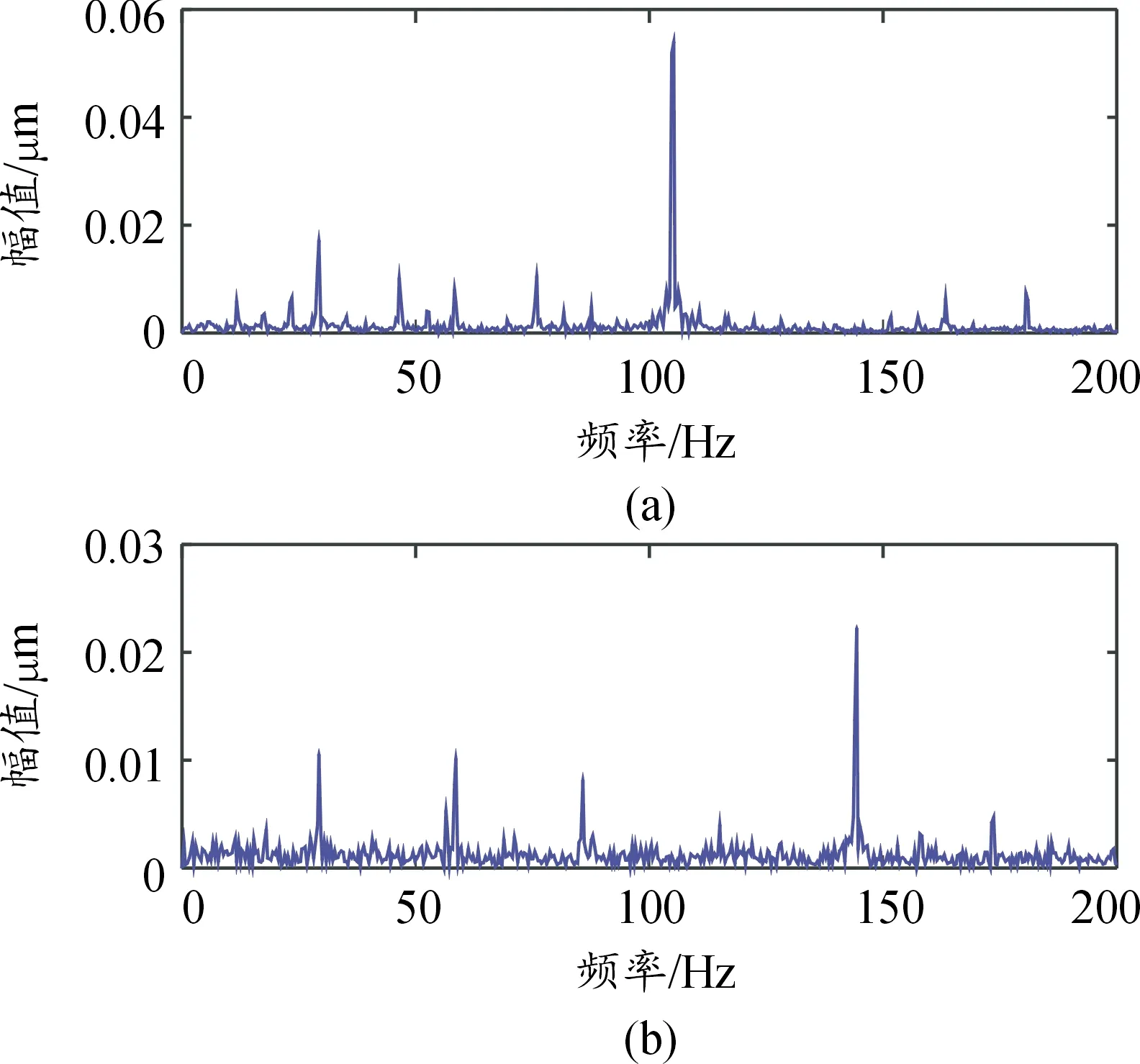
图13 源信号幅值谱图Fig.13 Altitude spectrum of source signal

图14 混叠信号时域波形图Fig.14 Time domain waveform of aliased signal

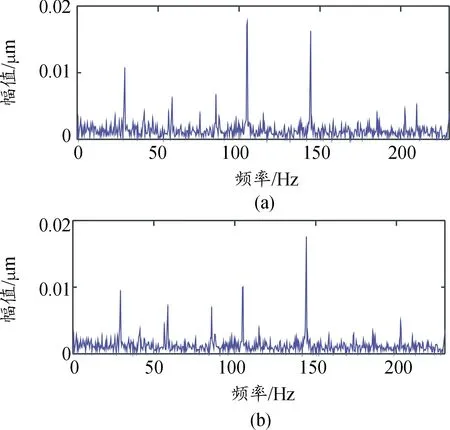
图15 混叠信号幅值谱图Fig.15 A ltitude spectrum of aliased signal

由图14的混叠信号时域波形图与图12源信号时域波形图对比可知，每一个通道采集得到的振动信号都是两个电机同时转动时信号的叠加。由图13的混叠信号的幅值谱图与图13的源信号幅值谱图对比可知，图15中两源信号的特征频率均同时在混合信号的幅值谱上显示，无法辨识各源信号的特征频率，所以两源信号完全混合。

用四线性平行因子盲分离算法分解得到的时域波形图如图16(a)与图16 (b)示，以及得到的幅值谱图如图17(a)与图17(b)所示。

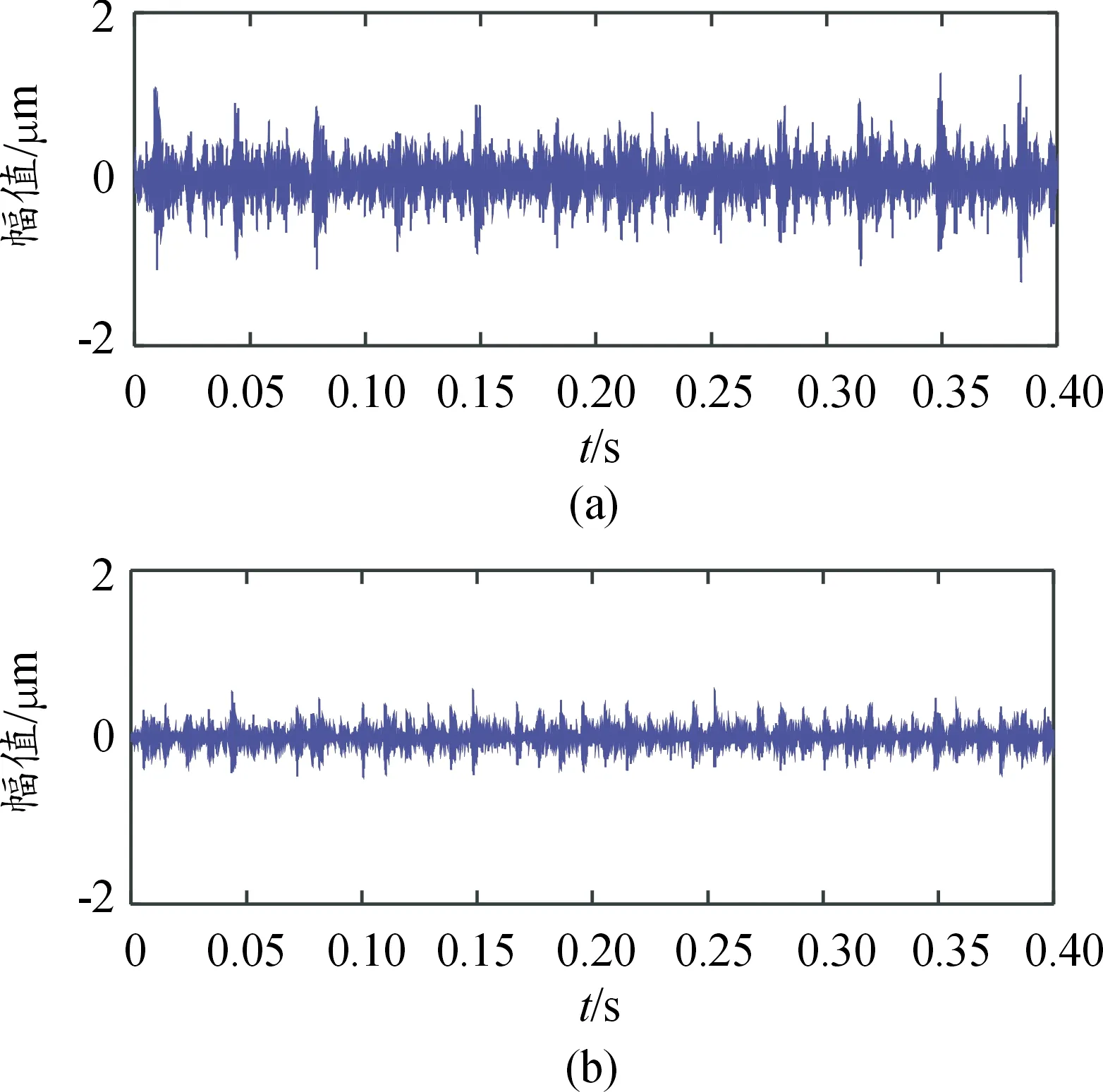
图16 恢复信号的时域波形图(四线性平行因子)Fig.16 Time domain waveform of recovered signal separated by quadrilinear parallel factor

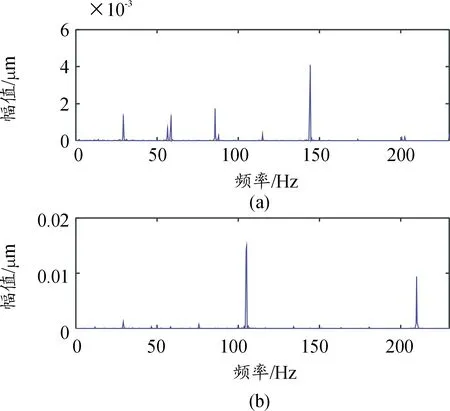
图17 恢复信号幅值谱图(四线性平行因子)Fig.17 Altitude spectrum of recovered signal separated by quadrilinear parallel factor

由图16可知，由图17所示的四线性平行因子盲分离方法能够分离分离混叠信号。由图17中(a)可知，特征频率主要为29.17 Hz、58.34 Hz、85.61 Hz、143.95 Hz，其分别对应着电机转频、转频的二倍频、二倍频与故障频率的叠加频率、以及故障特征频率。由其故障特征频率为143.95 Hz可知，该频谱为轴承外圈的故障。由图17中(b)可知，特征频率主要为29.17 Hz、104.31 Hz、208.61 Hz，其分别对应着电机转频、故障特征频率以及两倍故障特征频率。由其故障特征频率为104.31 Hz可知，该频谱为轴承内圈的故障。由图17与图12以及图14的对比(即四线性平行因子盲分离方法分离得到的时域波形图与源信号时域波形图的对比以及混叠信号时域波形图对比)可以发现，分离得到的时域波形图与源信号时域波形图有很高的相似度，分离效果良好。由图17与图13以及图15的对比(即四线性平行因子盲分离方法分离得到的幅值谱图与源信号幅值谱图以及混叠信号幅值谱图对比)可知，四线性平行因子盲分离方法成功分离了混叠信号，并且分离得到的信号特征频率与两源信号特征频率一致，但是由于盲分离本身模糊性的特性，会导致了盲分离得到的幅值谱图排序次序出现颠倒或者互换，这种排序及波形幅值的变换并不影响分离结果的准确性。从图17可以看出分离得到的幅值谱图除了排序及波形幅值有些变换外，恢复以及分离效果良好。四线性平行因子盲分离方法有效并且分离效果良好。

7 结论

本文提出基于四线性平行因子的机械故障盲分离方法，将三线性平行因子扩展到四线性，弥补了三线性建模时只对振动信号部分信息建模的缺陷，使数据包含的信息更完整。该方法在盲分离无需通道信息和源信号等先验知识的条件下能对分离出未知源信号，并且将盲分离与四线性平行因子在宽松条件下分解唯一性结合，在振动信号特征提取和信号分离时能充分发挥2种算法的优势。并且该方法使用四线性最小二乘法进行迭代拟合，相比于三线性平行因子迭代速度更快，迭代误差更小，迭代精确度更高。最后利用仿真和实验证实了所提的四线性平行因子的机械故障盲分离方法可以很好地提取故障特征并分离混合源信号。