基于前馈神经网络的柔性连续臂建模与仿真
范军红,朱云飞*,王文彪,鲍官军,姜利祥
(1. 可靠性与环境工程技术重点实验室; 2. 北京卫星环境工程研究所:北京 100094;3. 浙江工业大学 机械工程学院,杭州 310014)
0 引言
柔性连续体机器人手臂的研究近年来取得重大进展,研究人员根据不同的应用场景提出许多柔性连续体的原型,展示了其对多场景复杂环境的适应性。在航天领域,柔性连续臂在空间目标柔性捕获、航天器故障检测、辅助空间实验、行星地形探测等场景具有潜在应用价值。柔性连续臂可使用不同的驱动技术实现,如肌腱/缆绳、流体(气动或液压)肌肉驱动器、形状记忆合金以及介电弹性体驱动。通常情况下,柔性连续臂由3 个并列分布的驱动器构成,这是一个能够到达臂展范围内任意位置的最少驱动器数量配置。然而,由于缺乏运动学解耦和数值稳定的动态模型研究,柔性连续臂的建模特别是动态建模研究一直相对滞后。
刚性机械臂是高自由度的串行钢杆结构,假定钢杆不发生变形时,可以采用牛顿-欧拉递归法等高效算法进行明确的数学建模。而柔性连续臂模仿柔性无脊椎动物结构,在操作过程中会发生很大的变形,使得其数学建模极为复杂。柔性连续臂的运动方程大多依赖基于能量的模型来推导,针对柔性连续臂建模的一种常见思路是将柔性连续臂看作由多个虚拟离散小段刚体串联组成,然而这种思路由于自由度太多,在正、逆运动学求解中会遇到困难。为解决自由度太多的问题,可以使用形状函数(shape function)来描述柔性臂运动过程中的变形,这种方法被称为参数表示法。这些位移场通常表述为空间曲线或关节空间变量的多元多项式形式,构成可变形运动学模态方法的基础。
为了简化操作过程中的位置和姿态变化,研究人员提出了使用模态方法建立连续体机器人的运动学模型。早期研究者主要使用模态振型函数(mode shape function, MSF)来建立运动学模型。这种方法虽然简化了可变参数的数量,但通常需要组合多个形状函数来描述整个任务空间的参数变化,并且仅适用于变形较小的情况,局限性明显。2006 年Jones 和Walker 提出的曲线参数(curve parametric,CP)运动学模型是多截面柔性连续臂的高级运动学模型,并通过迭代方法产生准确的正运动学和逆运动学模型。该模型可以模拟任何柔性连续臂的弯曲运动,能紧凑表示实际关节空间变量(即驱动器长度)中的平滑弯曲,因此可以快速得到结果,并给出更好的物理解释。该模型有很多优势,启发了许多其他类似的运动学模型,并为柔性连续臂的相关研究提供了分析基础,但也存在一些缺陷——由于数值奇异性,它不能模拟连续体截面的直臂姿态(即当各驱动器长度相等时,完全地伸长或收缩运动)。基于CP 模型,研究者解决了其奇异性问题,扩大了CP 模型的应用范围,并对其逆运动学的数值解法进行了研究,但是其运动学模型求解存在不易收敛、耗时较长的问题。
考虑到上述模型及其求解中存在的局限性,本文提出采用神经网络对柔性连续臂运动学进行建模的方法,试图利用CP 和模态方法建立正运动学模型,产生关节空间向量到目标姿态映射的海量数据集DataSet,并利用此数据集建立基于前馈神经网络的正运动学和逆运动学模型,以期解决奇异性以及逆运动学求解不稳定问题,并显著缩短逆运动学求解的时间,为之后采用强化学习方法学习控制策略建立基础模型。
1 自研柔性连续臂介绍
1.1 设计描述
本文作者所属团队研发的柔性连续臂如图1 所示,采用分节设计,初步设计为3 节,每节由多根气动肌腱并联组成,采用自研的加压伸长型气动肌腱作为驱动器,可实现每节独立地弯曲和伸长。

图1 柔性连续臂实拍图Fig. 1 The flexible continuum arm
加压伸长型气动肌腱由内部硅胶管和外部限制其径向变形的波纹管构成。波纹管的伸长量来源于其轴向层叠的波纹结构,此结构使得气动肌肉的伸长量与纤维编织角度无关,突破了现有传统双螺旋编织网气动肌肉、囊颗粒型气动肌肉的设计局限。
在高压气体作用下,该气动肌腱最大能产生300%的轴向变形,气压降为所处环境大气压时可恢复为原来的形状。这在每个驱动器能够伸长和收缩的功能基础上,极大提高了柔性连续臂的弯曲致动性能和运动抓取的灵活性。
1.2 系统模型
为对柔性连续臂进行建模,需要抽象出其系统模型。因此,基于Godage 等2015 年建立的运动学模型给出该柔性连续臂第小段的几何模型,如图2 所示。

图2 柔性连续臂任意第i 小段的几何模型Fig. 2 Geometrical model of an optional part of the flexible continuum arm
为不失通用性,本文采用3 个可变长度驱动器的配置,将驱动器固定在一个半径为r的圆形刚构上,并按照2π/3 的弧度间隔分布,平行于一条假想的穿过截面中心点的线。驱动器的初始长度为L,伸长量为l,且l≤l()≤l,其中表示第小段,表示此小段的第个驱动器。因此,一个驱动器在任何时刻的长度为L()=L+ l()。为方便后文的描述,将第小段的伸长量组成关节向量q=[l()l()l()]。
2 运动学模型
本章对CP 模型进行推导,并总结分析采用模态方法建立的运动学模型,提出一种有效收敛的逆运动学求解方法。
2.1 曲线参数模型
基于可变长度驱动器的特点,柔性连续臂每一小段都能完成伸长、收缩和弯曲运动。因此,在忽略负载的情况下,连续体每一小段的空间姿态完全可以用一个变曲率半径和变长度的圆弧来表示。这个圆弧可由3 个空间参数定义——关于瞬时中心的曲率半径λ∈(0, ∞)、弯曲弧度φ∈[0, 2π)以及弯曲平面相对于+X的角度θ∈[-π, π]。关节空间变量中的3 个曲线参数的求解公式为
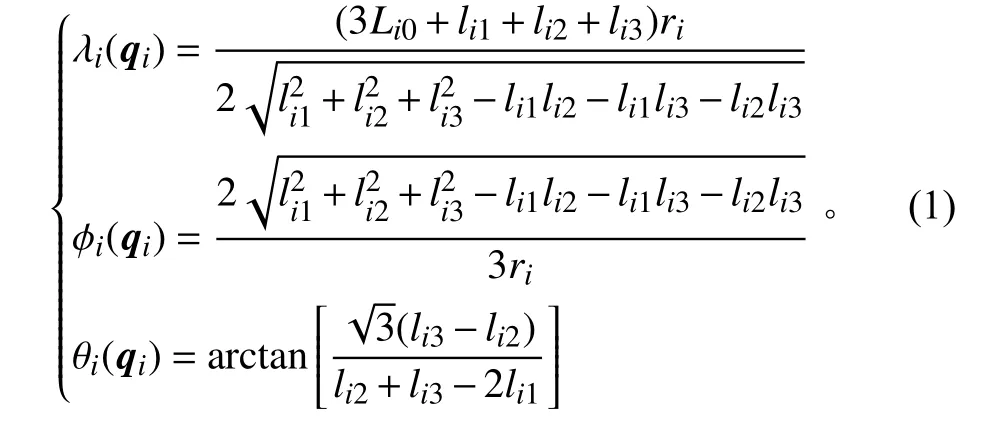
为了完成运动学建模,必须正确计算柔性连续臂的位置和姿态。由于连续体截面的固有力学变形较大,沿长度方向有变化,必须用齐次变换矩阵(HTM)来表示。在图2 中,定义了一个移动坐标系{´},并且引入一个标量参数ξ∈[0, 1]来描述移动坐标系{´}沿柔性臂中心轴线从起点(ξ=0)至末端点(ξ=1)的移动。最终,基于曲线参数模型的柔性连续臂第小段的 HTM 表达式为

正如式(1)所述,当3 个可变长度驱动器的伸长量相同(即柔性臂直线伸缩运动)时,第小段的曲率半径无穷大,曲线参数的HTM 描述失去意义。
2.2 基于模态方法的运动学模型及逆运动学求解

将该基于模态方法的运动学模型与自研的柔性连续臂实测数据进行对比,以证明该模型的有效性。图3 为1 根关节伸长48%、另外2 根关节不伸长的情况下,运动学模型(采用13 阶泰勒展开)与实测数据的对比,可以看到两者的偏差在5%以内。
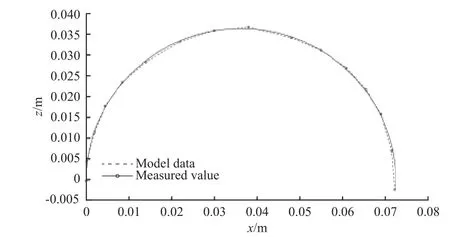
图3 模型数据与实测数据对比Fig. 3 Comparison between model data and measured values
对于逆运动学问题,适用于刚性机械臂的雅可比矩阵求逆方法失效,故考虑数值迭代的方法。逆运动学的目标是以任务空间的位姿信息作为约束条件,求解出关节空间的伸长量。关节空间到任务空间的映射为非线性关系,因此可将逆运动学视作一个约束条件下的非线性优化问题。本文尝试使用MATLAB 中的非线性约束问题求解函数,将目标姿态看作约束条件,求解出满足约束条件的关节向量值(即可变长度驱动器的伸长量)。
在求解过程中发现,只有目标姿态矩阵与初始姿态矩阵的欧氏距离极小时,此求解过程才能收敛。显然,这是不具有实用价值的。为此,本文提出建立一个从初始姿态矩阵到目标姿态矩阵转换的连续函数,并将连续函数产生的中间目标姿态作为求解过程中的临时姿态矩阵。图4 展示了沿着直线轨迹逼近目标姿态的逆运动学求解过程,其中虚线表示临时姿态矩阵形成的逼近轨迹,可以看出其完全按照直线轨迹逼近目标点。

图4 沿着直线轨迹的逆运动学求解示例Fig. 4 Example of inverse kinematics solution along a straight trajectory
图5 展示了沿着圆弧轨迹逼近目标姿态的逆运动学求解过程,虽然没有完全按照圆弧轨迹进行逼近,但是最终还是收敛到了目标点。没有完全按照圆弧轨迹逼近的主要原因是圆弧轨迹的前半段不在工作空间范围内,不可达。
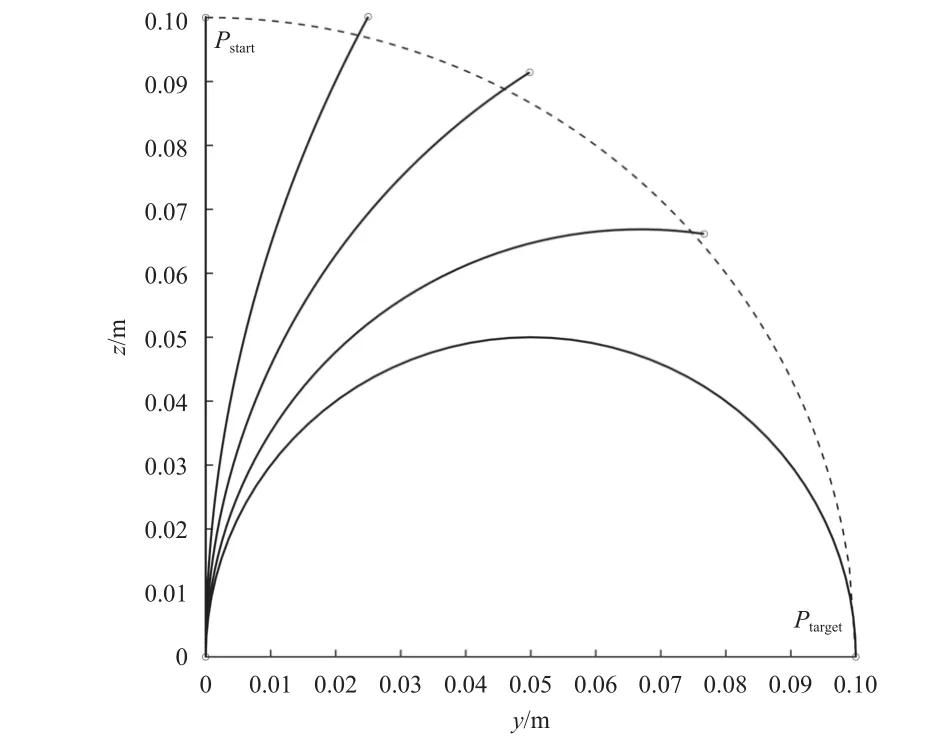
图5 沿着圆弧轨迹的逆运动学求解示例Fig. 5 Example of inverse kinematics solution along an arc trajectory
多次实验发现,添加临时姿态矩阵的方法成功解决了目标点与初始点相差较远导致不收敛的问题,但是,由于添加了很多的中间临时姿态矩阵,计算量和求解时间显著增加。
3 运动学模型拟合
上述运动学研究所用的临时姿态矩阵方法求解过程耗时较长,在逆运动学求解中尤为明显;而基于模型的强化学习方法来得到柔性臂的控制策略则要求求解时间尽量短。故此,本文提出使用前馈神经网络来拟合正运动学和逆运动学模型,以在保证精度的情况下缩短求解时间。
3.1 前馈神经网络简介
前馈神经网络是一种典型的深度学习网络。万能近似定理表明,如果一个前馈神经网络具有线性输出层和至少一层包含非线性激活函数的隐藏层结构,那么只要给予网络足够数量的隐藏单元,它就可以任意精度来近似从任何一个有限维空间到另一个有限维空间的Boral 可测函数。因此,前馈神经网络很适合用来拟合柔性连续臂的运动学模型(非线性函数)。
此外,神经网络可以灵活更改输入和输出神经元的数量,对应于柔性连续臂而言,意味着可以灵活更改关节空间变量和任务空间变量的数量,即能较容易地将1 节的模型迁移到3 节的模型中,并可以将任意点的位置和姿态视作任务空间变量来进行建模,从而显著提高模型的灵活性和普适性。
3.2 正运动学模型拟合
利用前面建立的正运动学模型,产生关节向量到末端姿态映射的100 000 个数据,作为训练数据集,其中关节向量在0~80%的伸长率区间里按照均匀分布产生;使用相同的方法产生10 000 个数据,作为测试集。然后将关节向量作为输入量,末端姿态作为输出量,训练一个前馈神经网络来拟合这个映射,从而求解出一个端到端的运动学模型,并在测试集上测试该模型的准确性。
本文设计了一个8层的神经网络,其输入输出层均包含3 个神经元,隐藏层的结构如图6 所示。在数据集预处理过程中,将其归一化为均值为0、方差为1 的正态分布数据集,故相应的激活函数采用双曲正切激活函数tanh。此模型本质上是一个回归模型,回归模型一般采用均方误差(MSE)作为损失函数。关于优化函数,采用目前最主流的Adam 函数,并取得了很好的效果。
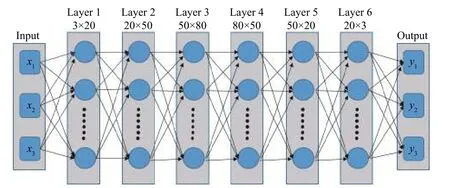
图6 前馈神经网络结构示意Fig. 6 Schematic diagram of feedforward network structure
训练过程中的超参数选择如表1 所示,其中学习率(learning_rate)为0.0001,这是在比较了学习率为0.001、0.005、0.0001 的效果之后择优选择的。批尺寸(bactch_size)和单次优化数据量(epoch)的改变对训练结果影响不明显。由于本文的训练集样本数量足够大,几乎涵盖了所有可能的输入情况,所以不考虑过拟合问题(有关参数weight_decay 的值很小)。
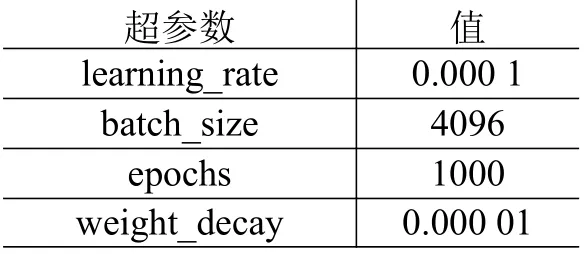
表1 正运动学模型拟合中的超参数选择Table 1 Selection of hyperparameters for forward kinematics model fitting
损失值(loss value)的优化曲线如图7 所示,可以看出,损失值在经过250 个epoch 时间优化之后较好地收敛到一个接近于0 的值,说明此模型在训练集上表现优异,有效学习到了关节向量到末端姿态的映射关系。

图7 正运动学拟合中损失值优化曲线Fig. 7 Optimization curve of loss value in forward kinematics fitting
之后,在测试集上测试模型的效果,并采用相对误差的平均值来评估模型的效果。的计算式为
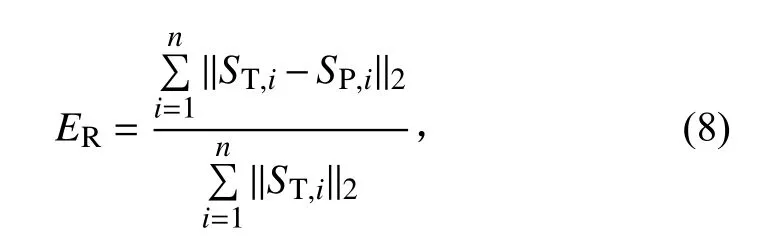
式中:表示测试集上第个样本的真实输出结果;表示第个样本的模型预测结果,并采用L2范数衡量输出向量的大小。
图8 展示了模型在测试集上的最终效果,可以看出,相对误差的平均值在0.055 左右,转换为绝对误差后稳定在5 mm 左右,符合柔性连续臂的控制精度要求。此误差来源主要是因为损失值的优化函数是随机梯度下降法,其最优值是一个相对效果很好的局部最优值,并不是绝对全局最优值。
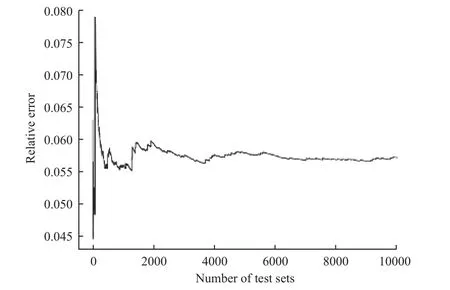
图8 正运动学相对误差平均值曲线Fig. 8 Mean value curve of forward kinematics relative error
3.3 逆运动学模型拟合
利用3.2 节生成的训练数据集,将末端姿态作为输入量,关节向量作为输出量,训练一个神经网络来拟合这个映射,从而完成逆运动学的求解过程。逆运动学与正运动学的神经网络结构完全相同(参见图6),不再赘述;部分超参数选择存在变化(参见表2),主要是对学习率进行了微调。
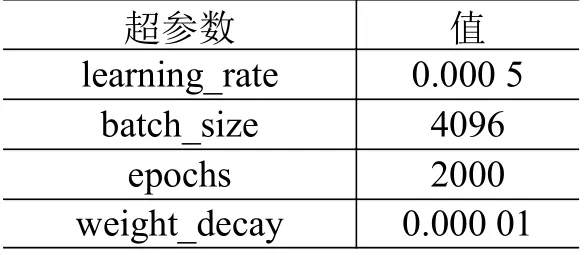
表2 逆运动学模型拟合中的超参数选择Table 2 Selection of hyperparameters for inverse kinematics model fitting
图9 展示了损失值的变化过程,从图中可以看出损失值在经过250 个epoch 时间优化之后接近完美地收敛于0,说明此模型在训练集上表现很好,学习到了末端姿态到关节向量的映射关系。
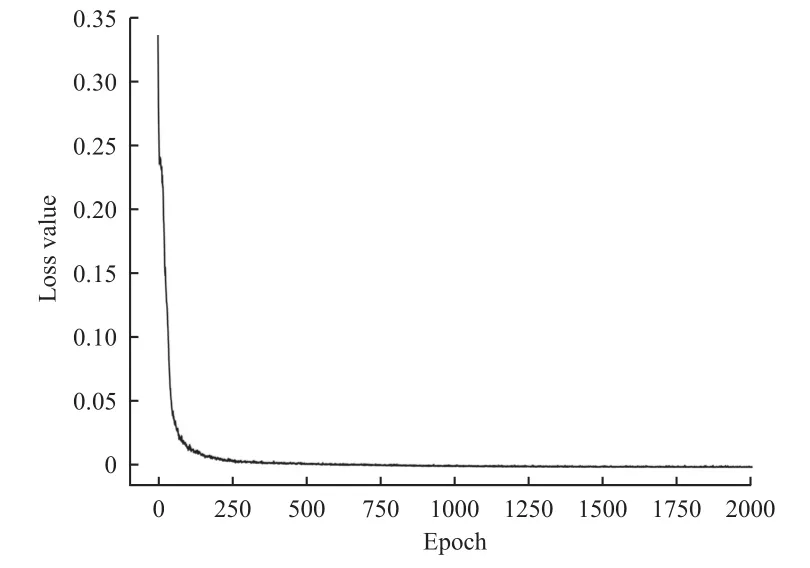
图9 逆运动学拟合中损失值优化曲线Fig. 9 Optimization curve of loss value in inverse kinematics fitting
图10 展示了逆运动学相对误差平均值,可以看出,其相对误差平均值为0.038 左右,转换为绝对误差约为4 mm,满足大部分柔性连续臂的控制精度要求,其误差来源已在正运动学部分予以解释。
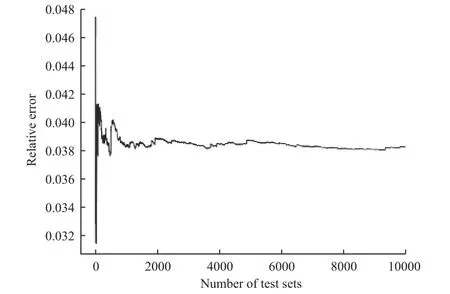
图10 逆运动学相对误差平均值曲线Fig. 10 Mean value curve of inverse kinematics relative error
此外,此逆运动学模型显著提高了求解效率。第2 章提到,利用临时姿态矩阵求解逆运动学的方法完成1 次逆运动学求解需要进行很多次约束条件下的非线性函数求解,而每次非线性函数求解需要进行很多步数的迭代,多次实验后得到其1 次逆运动学求解平均耗时14.4 s。而基于前馈神经网络的模型是一个端到端的数据驱动的模型,只关注输入/输出量,忽视过程量,且模型结构较小,因此能够很快给出结果,对数量为10 000 的测试集完成1 次测试所需的时间仅为1.5 s。
4 结束语
本文针对柔性连续臂逆运动学求解过程中不易收敛的问题,提出使用临时姿态矩阵进行逆运动学求解的方法。但是,这种方法存在求解时间过长,不适用于控制策略的学习等要求快速求解的过程。为此,又提出使用前馈神经网络对柔性连续臂进行正运动学和逆运动学端到端建模的方法,该方法的应用在保证模型精度的基础上,显著提高了逆运动学求解的效率,为后续柔性连续臂的智能控制策略研究奠定了基础。
(编辑:张艳艳)

