基于实时应变监测信息的钢筋混凝土梁有效疲劳应力参数值模型

刘芳平, 邓勇军, 易文涛, 闫 磊

(1. 河西学院 土木工程学院, 甘肃 张掖 734000； 2. 重庆三峡学院 土木工程学院, 重庆 404020; 3. 崇州市公路工程质量监督管理站, 四川 崇州 611230)

随着桥梁结构监测技术的发展，原有的交通荷载谱被实时得到的挠度-时程响应、应变-时程响应等代替[1]，更加真实和准确地反映了桥梁服役状态.这些技术进步为精确评估桥梁疲劳性能提供了必要的前提和基础.然而随监测时间增长，所得到的这些响应数据量越来越多，并且伴有失真、缺失、重复、随机出现等特点.所以，在进行桥梁疲劳评估时首先应保证监测数据的准确性和有效性.如何利用实时监测数据信息来分析结构的疲劳特征已成为当前的重要课题[2-5].

为获得反映钢筋混凝土梁真实响应状态的疲劳应力值，本文从实时应变监测信息出发，利用监测数据的周期循环特性将其按相似度简约处理为标准循环块，采用AIT(Average, interpolate,take-out，AIT)处理和傅里叶转换得到了反映结构真实响应的应变数据；然后基于动态应变标准循环块特征，运用改进的跨均值峰值计数法对随机波形应力峰值进行统计，通过转换得到桥梁真实疲劳应力特征值；再基于应变能及损伤等效原理将变幅应力谱值转换为形式简单、可以直接利用的等效疲劳应力谱值；最后建立了基于实时应变监测信息的有效疲劳应力参数值模型，并结合实际算例进行了验证分析.

1 基于实时监测应变的疲劳应力计算

要对钢筋混凝土梁进行实时、准确的疲劳性能识别评估，首先需获得结构服役期间的真实响应数据，如应变、挠度等.这些参数原始监测信息有一定的规律，但往往并非结构真实响应，其通常有如下特征：

1) 监测数据连续不断、数量巨大且复杂，原数据不易直接应用于计算分析；

2) 监测数据掺杂仪器误差、结构噪声、局部数据突变，可能造成原始数据部分失真；

3) 梁上车辆等荷载呈现相似性往复循环，所以监测的信息也呈现相似往复循环变化.

鉴于此，在进行结构疲劳性能评估时，应该将监测信息简化并进行相应处理，以实现结构真实响应数据的提取与验证.本文将监测应变简化为标准循环块，并采用AIT(“平均-插值-扣除”)手段进行低、高频运算，完成去噪取真，实现结构真实数据的提取；基于“傅里叶转换”进行时域-频域上不断转换分析及真实性验证，最终获得结构真实应变响应数据.

1.1 实时应变的简化与AIT处理

研究发现，梁上车辆荷载呈现周期性循环变化规律，即可认为梁结构所受荷载也呈现相似周期性循环变化规律.为此，可以将连续不断监测的实时应变数据用一个不断重复作用的标准循环块进行表示[6]，研究监测实时应变数据的问题可转化为研究标准循环块，并用它来推演梁结构实时疲劳有效应力.基于以上思路，可将实时应变监测数据按照式(1)进行阶段划分

(1)

式中:k表示全寿命中的阶段数，即总循环块数；Tf为结构服役寿命；T为标准循环块时间周期，考虑到车辆荷载施加的相似性，本文取T=7 d.式(1)即为钢筋混凝土梁在疲劳损伤过程中的阶段标准循环块划分计算式.每个阶段周期i内结构所受荷载、监测应变都具有相似性，都可以独立反映桥梁结构疲劳状态.

为克服应变监测数据因仪器误差、结构噪声等造成的局部突变、部分失真问题，实现真实数据的提取，本文采用AIT(“平均-插值-扣除”)手段将监测实时应变信息进行低频和高频运算，最终实现数据低频、高频分离[7].

设原始数据为x(i)，1≤i≤N,采样长度为N，x0(j)为分离后的低频数据,1≤j≤k(N=mk).首先将原始监测数据进行平均，可得到低频数据，计算如下式：

(2)

然后将式(2)所示低频数据用抽插方法推到平均值域，获得高频数据，计算如下式：

(3)

最后将低高频两组数据相减，实现数据分离：

(4)

本分离方法操作简单，分离后的应变数据结合时域、频域不断转换分析，可获得反映结构真实响应的应变数据.

1.2 实时应变时域与频域分析

1) 监测应变时域分析

对实时应变监测数据进行简化与AIT处理以后，再依照监测时间序列进行排布，得到相应周期应变-时程数据标准样本，并将此样本表进行统计平均，最后可以得到标准循环块的时域应力与时程的关系.

有时同样的荷载引起疲劳应力的时间不一样，有一定的随机性，统计分析时受应变幅值时间差异的影响，监测数据在时域出现不同应变值叠加、平均现象，偏离了梁的真实疲劳响应状况.因结构时程疲劳最重要的是应力值场大小，其出现时间不是很重要，因此可通过时域-频率转换将监测数据转换到频率上进行分析来避开时域分析的差异影响.

2) 监测应变频域分析

将监测得到的循环块应变-时程数据在完成时域分析之后，按照式(5)进行快速傅里叶转换，得到应变-频域值：

(5)

然后依据(6)式进行线性回归：

y*=b0+b1x1+b2x2+...+bnxn

(6)

式中：y*为变量y的统计估计值，x1,x2,…,xn为监测应变；b1,b2,…,bn为回归系数；b0为回归常数.

为检验转换的域谱值能否反映真实情况，可通过频域-时域之间的反复转换误差大小来判断，如式(7)所示：

(7)

如果所得误差值满足一定要求(小于5%)，那么转换结果满足真实性；同时可以将转换结果与原始样本时域结果来进一步比较，对图形相似度进行检查，如果相似，说明频域结果可以反映结构真实动态响应，反之频域数据结果失真，需进一步分析去杂.

基于监测应变数据频域-时域转换及进行真实性验证，可得到时域/频域上的真实应变响应特征循环域值，即可得到反映桥结构动态性能的标准循环块值场.

2 基于改进跨均值峰值计数法的疲劳应力特征值分析

2.1 实时疲劳应力数据计算

实时疲劳应力无法直接监测得到，要通过监测的实时应变与弹性模量乘积来表达，但是循环荷载作用下混凝土应力应变关系超出了弹性范畴，所以，基于弹性阶段得到的应力数据与实际相差甚远.对循环荷载下弹性模量的研究，雷俊卿等[8]、孟宪宏[9]、朱劲松[10]学者都给出了自己的表达式，但普遍存在影响参数多，不便于应用等问题.本文采取李秀芬[11]疲劳研究得到的弯曲变形模量与受压弹性模量关系，如下式：

Eb=0.875E

(8)

同时，得到的疲劳变形模量降低系数回归方程如式(9)所示：

γf=0.982-0.027logn

(9)

式中:γf为疲劳变形模量的下降系数,γf=Efb/Eb；Efb是疲劳变形模量；n是疲劳荷载循环次数.

结合式(8)和式(9)可得到疲劳变形模量为

Efb=(0.86-0.024logn)E

(10)

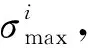
σ(t)=ε(t)·Efb=ε(t)(0.86-0.024logn)E

(11)

2.2 疲劳应力特征参数分析

依据本文思路，后续要进行的梁结构疲劳状态评估最终落脚点在结构疲劳应力上，虽然经过以上方法得到的时域/频域应变场数据结合公式(11)得到的应力场数据能够反映结构真实响应，但是如果用于疲劳计算分析，还需要进一步提取特征值.

本文疲劳应力特征值就是应力数据中波形峰值循环值，即标准循环块值场.要获得这一特征值，就必须对梁荷载(复杂随机载荷)形成的波形中应力峰值出现的次数加以累计，即统计载荷-时间历程曲线峰值出现的次数.目前主要统计方法有取点计数法、穿级计数法、峰值计数法、变程计数法等.

本文针对动态应变标准循环块的显著个性特征将峰值计数法改进与发展，使其更适用于钢筋混凝土梁结构响应实时应变监测数据处理[12].因材料处于弹塑性阶段时残余应变才会产生，并且弹塑性区中间应力波形对应幅值对残余应变贡献比较小.本改进跨均值峰值计数法假定如下：

1) 为了只计两次均值间更主要峰值，忽略中间波形对应幅值或者载荷波动的影响；

2) 将材料比例极限σc作为读数起点来代替均值线，并且只有σ(t)<σc时才对极大值进行计数，如图1所示.

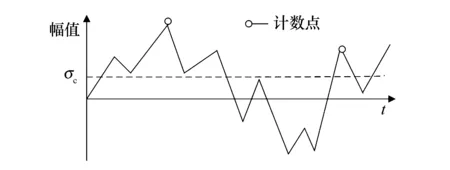
图1 改进的跨均值峰值计数法Fig.1 Improved cross-mean peak counting method

在获得应变特征值后，再通过式(11)转换为应力，变成标准循环块疲劳应力特征值.通过以上分析

(12)

3 建立有效疲劳应力参数值模型

综上得到的疲劳应力特征值可以直接反映梁结构的疲劳响应，但是其出现概率具有随机性，大小变化具有偶然性，是变幅应力，如果直接用于桥梁结构疲劳性能评估操作困难并且不容易实现.所以，在不影响梁结构疲劳损伤前提下还需将上述疲劳应力特征值进行转换，采用一种直接、简单、高效的等效疲劳应力谱值来代替原有的变幅应力谱值对梁结构疲劳状况进行评估.

3.1 基于应变能及损伤等效原理的变幅应力有效应力谱计算

有效应力谱计算普遍采用的方法是基于Miner[13]理论导出的等效等幅计算公式，它形式简单，操作方便，但是计算精确较低，疲劳评估效果一般.本文采用基于应变能及损伤等效原理来计算变幅疲劳的有效应力谱[14].基于以上原理通过相应疲劳模型来计算有效应力谱时首先应该满足以下两条准则：

准则二：变幅疲劳应力谱在梁结构上产生的疲劳损伤Di和等效应力谱产生的疲劳损伤Def等效，即：Def=Di；

1) 基于准则一的有效应力参数分析

梁在疲劳循环过程中，结构疲劳总变形为弹性形变和塑性形变之和，即：

ΔW=ΔWe+ΔWp

(13)

式中：ΔW为总的应变能密度；ΔWe为总的弹性应变能密度；ΔWp是总的塑性应变能密度.

梁结构疲劳属于高频小变形，大塑性变形可以忽略不计，即塑性应变能贡献可略去不计，因此在正常服役中结构可以用弹性应变能密度来代表总应变能密度.

由弹塑性力学可知，变幅应力产生的应变能密度为

(14)

恒幅应力产生的应变能密度为

(15)

依据准则一的规定，结合式(14)和式(15)得到：

(16)

即

(17)

式(17)没有考虑平均应力情况并且假定应力比率R=-1,σm=0.

2) 基于准则二的有效应力参数分析

准则一的计算理念是基于应变能密度等效，并没有考虑结构的疲劳损伤，下面是基于疲劳损伤等效分析有效应力的计算方法.

梁结构高周疲劳损伤的损伤率可表示为[14]

(18)

恒幅疲劳下的疲劳损伤率可表示为

(19)

依据准则二的规定,结合式(18)和式(19)得到：

(20)

式中：Δσi和σmi分别是变幅应力幅值和均值；β为材料参数，采用疲劳试验进行拟合.

由式(20)可知，有效应力虽然考虑了材料参数β，但未考虑损伤变化影响.梁结构疲劳中的非线性变化一般用参数α来表达，即αi=f(Δσi)，因此在考虑损伤非线性累积下有效应力幅值应为

(21)

式(21)即为满足以上两条准则的有效应力计算表达式，可用于梁结构疲劳损伤计算应力值.

3.2 基于结构损伤实时性计算分析的有效疲劳应力参数值模型

从损伤计算和疲劳应力谱之间的关系出发直接分析疲劳有效应力峰值是比较困难的.因此本文按照以往试验和研究经验用阶段性有效应力幅来表示有效应力峰值表达式.

李兆霞[14]、朱红兵[15]、 冯秀峰[16]等的研究结果均显示，梁结构服役期间混凝土应力峰值的增加要比应力幅的增长快很多，而且应力峰值存在明显的三阶段变化规律.依据已有研究成果，在式(21)的基础之上考虑用增长率修正系数ζ(x)来模拟梁结构正常使用阶段的有效应力峰值，用Matlab拟合得到的ζ(x)表达式如下：

(22)

式(22)是基于文献试验拟合的经验关系式，反映梁结构疲劳循环下的有效应力峰值增长率受疲劳次数及损伤度的影响.

综合式(17),式(21)和式(22)可以得到考虑有效应力幅速率影响下基于应变能及损伤等效原理的阶段疲劳有效应力峰值表达式:

按照以上计算流程，可得到梁疲劳损伤有效应力变化特征曲线.对桥梁进行实时疲劳损伤性能评估时，可用式(25)的有效应力值场并依照阶段标准循环块进行计算分析：

(25)

因实时性计算基于直接监测的应力数据，其已包含了疲劳损伤影响，是结构响应值，故无需考虑非线性影响，可直接采用等效应变能准则来进行计算.

若需根据当前监测应变信息以及梁结构疲劳状态来预测以后结构疲劳损伤，可以使用公式(26)进行计算：

(26)

式(26) 不但可以对实时应变监测数据的计算结果进行对比分析，而且对梁结构安全起警示与预测作用.但后期损伤情况和预测的寿命是基于目前应变监测数据，所以还应该考虑后期损伤的影响.

3.3 有效疲劳应力参数值模型计算流程

根据本文分析，可以将基于实时应变监测数据的有效疲劳应力参数值计算流程归纳为7个步骤.

1) 记录原始监测数据ε(t)，并以7天为模块进行阶段划分；

2) 通过“平均-插值-扣除”(AIT)手段将原监测数据进行低、高频运算，完成去噪取真，实现结构真实数据的提取；

3) 基于“傅里叶转换”将监测数据在时域-频域上不断转换分析并进行真实性验证，获得结构真实应变响应特征循环域值；

4) 按照公式(11)进行实时疲劳应力数据计算；

6) 按照式(24)计算变幅应力的有效应力谱；

7) 按照式(25)进行结构实时性损伤的有效疲劳应力参数值模型计算分析，得到梁疲劳损伤有效应力特征曲线.

4 模型实例分析

本文以重庆市丰都县龙河特大桥[12]的应变监测信息为依据进行分析.取主跨跨中2#截面顶板处编号为S0303应变传感器实际监测的应变信息分析结构损伤实时性有效疲劳应力参数值模型.本文取三周数据并按照本文提出的上述方法进行计算分析.大桥分析计算时建立的模型如图2所示，主要控

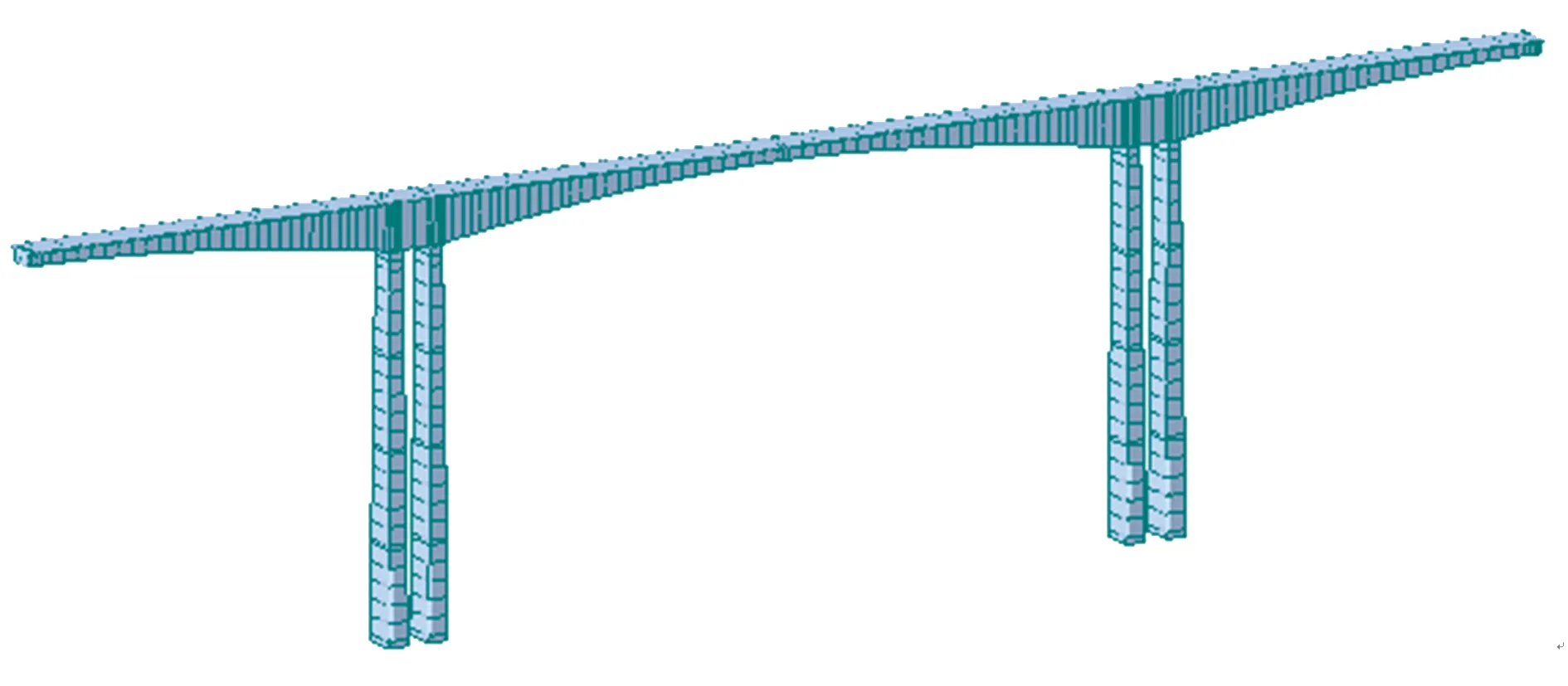
图2 龙河特大桥模型

制截面应力测点立面布置示意如图3，跨中2#截面应力传感器布置图示意如图4所示.

图3 主要控制截面应力测点立面布置示意Fig.3 Schematic diagram of the elevation layout of the stress measuring point of the main control section

图4 2#截面应力传感器布置示意

4.1 监测应变数据处理

原始监测应变数据信息如图5所示.按照式(1)将监测系统下的应变数据进行阶段划分，得到标准循环块如图6.

图5 原始监测应变

根据图6的标准循环块采用AIT方法进行运算，再进行时域及频域上的分析，得到反映桥梁结构实际响应数据，如图7所示.再将以上应变样本数据进一步转化为应力数据，得到应力标准循环块，转化结果如图8所示.

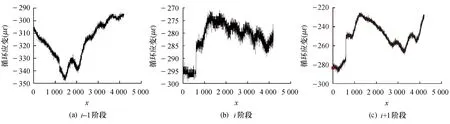
图6 监测应变划分的标准循环块

图7 阶段循环块监测应变数据样本曲线

图8 阶段循环块应力数据样本曲线Fig.8 Data sample curve of phase cycle block stress

4.2 获取结构疲劳应力特征量

图9 计算截面特征参量计数Fig.9 Counts of feature parameter for calculate section

统计采用本文方法得到的特征参量，可以获得所采用数据循环阶段疲劳特征参量如图10所示.

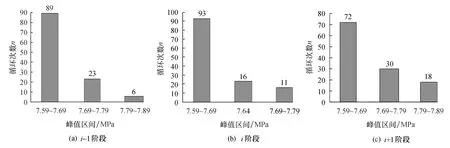
图10 计算截面特征参量统计结果Fig.10 Statistical results of features parameter for calculate section

4.3 有效疲劳应力参数值模型计算

获得疲劳特征参量后，再根据本文计算式(25)计算疲劳应力上限取1/m=0.378.最后计算得到的标准阶段有效疲劳应力上限峰值如表1所示.

表1 标准循环块有效疲劳应力特征值

由表1可知，随着桥梁工作年限逐渐增长，结构疲劳应力逐渐增加，损伤不停累积.

5 结语

1) 基于实时监测应变数据的周期循环特性，本文将其简化为标准循环块，采用“平均-插值-扣除”手段进行了低、高频运算，实现了结构真实数据的提取；基于“傅里叶转换”对其进行了时域-频域上的转换分析及真实性验证，最终获得了反映结构真实响应的应变数据.

2) 基于动态应变标准循环块的显著个性特征，在对梁结构随机载荷的波形应力峰值次数进行统计时，本文只计两次均值间主要峰值，并将材料比例极限σc作为读数起点，将跨均值峰值计数法进行了改进，使其更适用于钢筋混凝土梁实时应变监测数据的统计；在获得应变特征值后，通过转换得到梁真实疲劳应力特征值.

3) 在不影响梁疲劳损伤前提下，基于应变能及损伤等效原理将变幅应力谱值转换为形式简单、可以直接利用的等效疲劳应力谱值，建立了结构损伤实时性计算分析的有效疲劳应力参数值模型.