机器学习模型与遥感反演水深的对比研究
纪 茜,沈 蔚,饶亚丽,孟 然
(1. 上海海洋大学海洋科学学院,上海 201306;2.上海河口海洋测绘工程技术研究中心,上海 201306;3.南通智能感知研究院,江苏 南通 226000)
引 言
水深是重要的地形要素,水深的测量有助于更好的了解浅海的地形地貌,也对近海开展经济和军事等活动有很重要的作用[1]。水深遥感反演因为覆盖面积大、更新快和成本低的优势而成为测量水深的一种重要手段,也是对传统水深测量方法和技术的补充和改进。遥感反演水深的原理是利用遥感影像,根据能够测得的与水深相关性高的参数来反演水深值[2]。
目前,反演水深的模型主要有理论模型、半理论半经验模型和统计模型,其中半理论半经验模型应用比较广泛,常见的有线性回归模型、双波段比值模型和神经网络模型[3]。Lyzenga[4]等在底层反射模型的基础上,提出水深值和辐亮度之间的线性关系,从而获得水深信息。Stumpf[5]等人提出了根据波段之间的比值与水深的线性回归关系来获取水深值,这在一定程度上消除了浅海中不同底质带来的影响。王晶晶[6]等通过不同的模型和方法探讨反射率的一阶微分与水深之间的回归关系,证明水深与水体反射率在近红外波段相关性最好。为了提高反演精度,很多学者开始利用神经网络进行水深反演,通过建立水深与反射率之间的非线性关系来反演水深。Sandidge[7]等利用BP神经网络建立了遥感反射比与实测水深之间的相关模型。Anctil[8]等利用神经网络捕捉水深波动的复杂变化,分析输入延迟神经网络、递归神经网络和RBF等3种网络建立的水深波动模型的效果,得出递归神经网络更适合反演水深。邓正栋[9]等分别建立了BP(Back Propagation)和RBF(Radial Basis Function)的水深反演模型,并与单波段、多波段模型进行比较,得出RBF模型反演精度更高。郑贵洲[10]等也建立了BP和RBF人工神经网络水深反演模型,得出RBF模型结构更简单,对样本要求低,反演精度高。Tatsuyuki Sagawa[11]等提出了一种基于随机森林和多时相卫星图像的浅水测深制图方法,建立了广义深度估计模型,对高透明条件下的浅水区域研究提供了方法;Yuan Qiangqiang[12]等系统总结如何利用传统的神经网络和深度学习方法来推进环境遥感的过程。
本文以甘泉岛为例,利用WorldView-2遥感数据和激光测深数据建立了BP神经网络、随机森林和极限学习机的水深反演模型,并进行精度评价,旨在找出适合研究区每个深度范围的反演模型和参数。
1 遥感反演水深
1.1 BP神经网络法
BP(Back Propagation)神经网络[13]是一种按照误差反向传播训练的多层前馈神经网络。此网络的主要特点是信号前向反馈,误差反向传播。在前向传递中,输入信号从输入层经过隐含层逐层处理,直到输出层。每一层的神经元状态仅影响下一层的神经元状态。假如实际输出与期望输出不相符,则转入反向传播,将输出误差通过隐含层向输入层逐层反转,并将误差分给各层的所有神经元,从各层获得的误差信号来调节网络权值和阈值,经过不断地训练,使BP神经网络预测输出值逼近期望输出值。
1.2 随机森林
随机森林(Random Forest,简称RF)是一种有监督学习的算法,它是以决策树为学习机器的集成学习算法。在算法中,可以同时生成多个预测模型,并通过综合分析各模型的预测结果来提升预测准确度[14]。
假设训练数据中有M个样本单元,N个变量,随机森林模型的构建过程如下:
1)从原始训练数据中有放回的随机抽取M个样本,进行采样,生成训练集。未被抽到的样本数据组成了袋外数据集,生成决策树。
2)在每棵树的每个节点处,随机抽取n 3)每棵树进行递归分割,直到该节点所有训练样本都属于同一类,此时不再进行分割。 极限学习机(Extreme Learning Machine, ELM)是2004年由南洋理工大学黄广斌副教授提出的[15],其主要特征是隐含层节点参数可以是随机或人为给定的且不需要调整,学习过程仅需计算输出权重。在文献[16-17]中可以看到ELM应用效果较好。ELM具有学习效率高和泛化能力强的优点,被广泛应用于分类、回归、聚类、特征学习等问题中,在计算过程中不需要调整输入权值和隐元的偏置[18],基本思想如下: 假设有N个样本(xi,yi),其中xi=[xi1,xi2,…,xin]T∈Rn,yi=[yi1,yi2,…,yin]T∈Rm,g(x)为激活函数,隐含层数目为L,则ELM模型可以表示为 (1) 其中,j=1,2,…,N;wi=[wi1,wi2,…,win]T表示输入节点和第i个隐含层节点之间的权重;βi=[βi1,βi2,…,βim]T表示第i个隐含层节点与输出节点之间的权重向量;bi表示第i个隐含层节点的阈值。ELM模型的矩阵表示形式为: Hβ=Y (2) 当激活函数g(x)无限可微时,权值w和b是可以随机选择的,而且在训练的时候保持不变。因此训练ELM就可以转化为计算Hβ=Y的最小二乘解问题。 ELM算法有3个步骤: 1)确定隐含层神经元个数L; 2)选择一个无限可微的函数来作为隐含层神经元的激活函数g(x),进而计算隐含层的输出矩阵H; 本文选取西沙群岛中的甘泉岛作为研究区域,研究区的范围为118°34′41″~111°35′38″E,16°29′56″N~16°31′17″N。本文所采用的遥感影像是2014年4月2日03:33分(格林尼治时间)获取的高分辨率WorldView-2多光谱遥感影像,一共有蓝、绿、红和近红外四个波段,空间分辨率为2 m。对研究区域进行辐射定标、大气校正、耀斑改正等预处理。实测水深数据为Leica hawk eye系统测量的甘泉岛激光测深数据,利用了Terrasolid中的Terrascan和Terramatch模块对LAS格式的机载激光点云数据进行了航带拼接、裁剪、异常点的剔除、海岛点云提取等过程,将与岛屿距离大于100 m的点的平均水面高程作为测量时的平均海平面,经过高程过滤,得到了水面以下的高程点,精度为分米级。随机抽取了494 个水深点,353 个用来反演水深,其余141 个用作精度检验,如图1所示。 图1 水深实测数据和遥感影像Fig.1 Measured data and remote sensing image of water depth 水深与多光谱影像较多波段存在线性关系,因此尝试通过波段敏感性分析的方法来选取反演模型输入参数,敏感波段的判断方法是将水深实测值与遥感影像的不同波段组合之间建立Person相关系数,并将其作为判断水深与遥感影像各波段相关程度的判断依据,Person相关系数的计算公式为: (3) 为了保证模型的适用性,在所有实测点中随机选取一部分作为进行建模的控制点,其余点作为模型验证的检查点。根据相关性分析,选择WorldView-2多光谱影像波段的B1, B2,B3,B4及各波段之间的比值B1/B2,B1/B3,B1/B4,B2/B3,B2/B4,B3/B4共10个值作为自变量,利用影像各波段的光谱反射率及反射率比值作为模型的输入值,把对应的实测水深值作为模型的输出值,利用控制点建立模型,利用检查点进行模型的验证,根据模型的评价指标,判断出适用性最强的模型。 在建立模型的过程中,BP神经网络需要设置大量的参数,为了得到最佳的反演模型,需要不断的改变神经元的个数、隐含层函数和输出的函数,需要花费大量的时间。而随机森林和ELM具有自主学习的能力,可以通过样本自动调节参数得到最佳的反演模型。BP神经网络模型是利用Matlab编程实现的[19],通过不断的训练和调整,最终确定的参数为:训练函数为trainlm,输入层节点为10,隐含层节点为5,最大训练次数为1000,训练要求精度为0.000 04,学习率为0.1。随机森林是利用R语言编程实现的,确定出算法中的回归树个数n为1000,分割节点所需的变量数目m为6。极限学习机模型是在Matlab平台上实现的,输入权重矩阵为训练集的输入矩阵,偏移矩阵为训练集的输出矩阵,隐含层神经元20 个,传递函数为Sigmoidal函数,类型选择回归。 将检查点用建立的BP神经网络模型、随机森林模型和极限学习机模型分别进行拟合,计算出水深反演值,对比各模型的反演值和实测值之间的误差,进行模型的精度验证及分析。为了定量的比较各模型的反演效果,采用决定系数(R2)评价模型的优劣性,均方根误差(RMSE)、平均相对误差(MRE)和平均绝对误差(MAE) 3个统计参数作为水深反演精度的评价指标,对模型水深反演值与水深实测值进行回归分析,比较各模型的反演精度。 (4) (5) (6) (7) 式中,Pi为第i个检查点的水深反演值;Yi为第i 个检查点的水深实测值;Y是指实测水深的平均值;n是指检查点的水深反演值检查点的数量。当决定系数R2越大时,表示实际水深值和反演水深值相关性越大,反演效果也越好。RMSE越小,表示水深反演误差的波动越小,反演效果越好。MAE越小时,表示实测水深值与反演水深值误差的绝对值越小,反演效果越好。MRE越小时,表示反演的可信程度越高。 将BP神经网络、随机森林、极限学习机三个模型进行比较,绘制了实测值与反演值1:1的关系图(如图2所示)。从图2中我们可以看出,整体拟合都比较紧凑,三个模型反演的水深与实测的水深有显著的相关关系。BP神经网络、随机森林、极限学习机模型反演结果误差分析如表1所示。由表分析可知,BP神经网络、随机森林、极限学习机模型的决定系数R2整体都很大,达到了0.95以上。3个模型的均方根误差(RMSE)和平均绝对误差(MAE)都是随着水深的增加而变大,平均相对误差(MRE)都是随着水深的增加而减小。 表1 水深反演模型反演结果Table 1 Results of water depth retrieval model 图2 水深反演值与真实值1:1关系图Fig.2 1:1 Relation between theretrieved value of water depth and the true value 在0~2 m水深范围内,均方根误差和平均绝对误差较小,而平均相对误差较大,这是因为在靠近海岸的区域,波浪较多,容易受到白色浪花以及沿岸的其他物质的影响。其中,RF的误差是最小的,这可能是因为在建立决策树时,它可以在内部对于一般化后的误差产生不偏差的估计。在2~5 m内,平均相对误差很明显的减小,反射率变化较小,在这个区域生长着一些水生植物,水体性质类似,因此反射率变化小。其中ELM的误差是最小的,ELM的反演效果更佳。在5~15 m内,水质逐渐清澈,影响因素减少,三个模型的反演效果差不多。在15~20 m处,建模所用的水深点较少,随机森林和极限学习机的误差差不多,明显小于BP神经网络。总体来说,在0~2 m处,随机森林效果更好,在2~5 m处,极限学习机更好,其他水深范围内,二者反演效果相当。 本文采用WorldView-2遥感影像与激光测深数据,利用BP神经网络、随机森林、极限学习机模型对甘泉岛进行0~20m内的浅海水深反演,并同前人使用的非线性回归模型进行横向对比,其中,郭晓雷[20]等利用单波段线性回归模型、双波段比值模型和多波段线性回归模型开展了遥感水深反演;吴忠强[16]等利用双波段比值回归模型、BP神经网络和极限学习机进行水深反演;邱耀炜[21]等利用单波段模型和双波段比值两个线性回归模型和随机森林模型反演水深;以上结果均表明利用机器学习方法反演水深的模型精度比传统的线性回归模型精度低,且机器学习拟合能力更强;相比于BP神经网络,极限学习机、支持向量机和随机森林等都有较好的反演精度。结果分析表明:总体上,利用机器学习的非线性回归模型反演水深的效果比较理想,对于机器学习模型,输入层、权重和函数都会对模型的水深反演效果产生影响,因此需要多次实验反复确定,以得到最适合的反演模型。对于不同的水深范围,其反演水深效果最好的模型也不一样,这可能是因为影响每个水深范围的因子不同。在小于5 m的水深范围内,靠岸近,悬浮泥沙和人工垃圾较多,影响反演效果。在大于15 m的水深范围内,由于水体深度逐渐变大,光在水体中的穿透力变弱,因而影响反演效果。 本文研究结果是根据甘泉岛WorldView-2遥感影像和激光测深数据得出的,结论与其他研究成果基本一致。现有研究大多数是基于线性回归模型和非线性回归模型来对比,本文重点比较机器学习的各模型的差异。但还存在一些不足之处,在建立使用机器学习的水深反演模型时,以训练误差为标准来确定隐含层节点的个数,这样很难找到真正的最优解,在一定程度上会影响反演的效果。在今后的研究中,应该对参数的选取以及个数进行优化,对模型进行优化,并且提高模型的适用性。1.3 极限学习机法

2 遥感反演水深实验
2.1 研究区与数据

2.2 相关性分析

2.3 实验过程
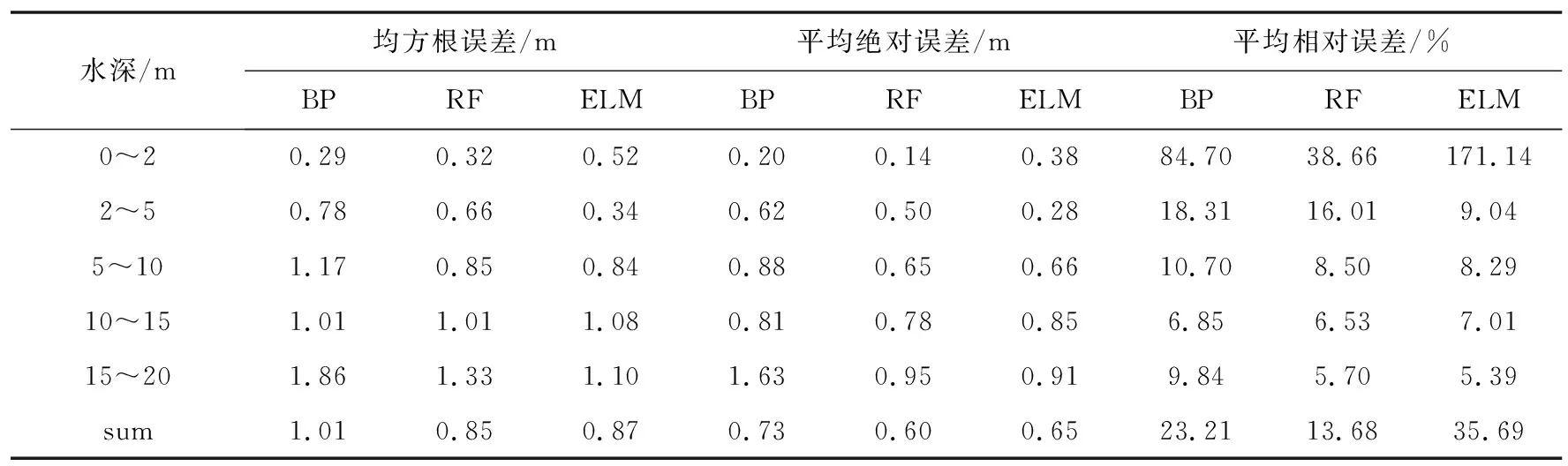
2.4 水深反演及结果分析

3 结论

