基于四元数傅里叶变换的低照度彩色图像增强算法

天津理工大学中环信息学院 乔兆亮 盖琦

针对低照度条件下彩色图像的细节丢失与视觉效果不佳等问题，提出了一种基于四元数傅里叶变换的彩色图像增强算法。把彩色图像表示为一个四元数矩阵，整体做傅里叶变换，设计频域滤波器，对图像做滤波处理。实验结果表明，该算法能够明显提升低照度彩色图像的视觉效果。

随着计算机和网络技术的发展，图像已经成为信息表达的一种重要方式，图像作为一种载体，是信息的最直观的表示。但图像在拍摄过程中会由于光照不足、噪声等因素影响，使得图像的视觉质量无法令人满意，需要做增强处理。图像增强的方法按照作用域的不同，可分为空间域和频率域，其中频率域滤波需要对图像做傅里叶变换，在变换域实现滤波处理[1-4]。

彩色图像由三个独立分量组成，如在RGB空间，由R、G、B三个分量组成，一般对于彩色图像的处理方法，是各个分量单独进行处理，如果在频率域滤波，需要针对三个分量做三次傅里叶变换，这样就忽略了彩色图像各个分量之间的内在联系。应用四元数理论，可以把彩色图像的像素作为一个矢量整体进行处理，只需要做一次四元数傅里叶变换即可，体现了图像的色彩关联[5-7]。

1 频域滤波器设计

图像频域滤波原理框图如图1所示。

图1 频域滤波原理框图Fig.1 Principle block diagram of frequency domain filtering

图中f(x,y)表示原始图像，g(x,y)表示处理后的图像，DFT代表离散傅里叶变换，DFT-1代表离散逆傅里叶变换，F(u,v)表示f(x,y)的频谱，H(u,v)代表滤波器。只要设计一个合适的滤波器H(u,v)，即可消除低频或高频成分，得到增强后的图像。本文选择的H(u,v)三维立体图如图2所示。

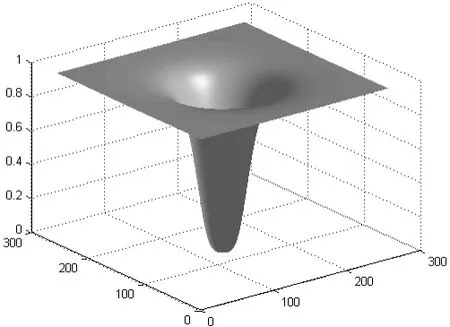
图2 H(u,v)三维立体图Fig.2 Three dimensional stereogram of H(u,v)

滤波函数可由公式（1）表示为[8]：

其中，D0代表截止频率，rl和rh的取值决定了滤波器对低频和高频分量的影响，c用来控制滤波函数斜面的锐化程度，若选择rl<1，rh>1，将同时实现抑制低频和增强高频的目的，可以使图像在压缩动态范围的同时增强图像的对比度[8]。

2 彩色图像的四元数傅里叶变换

一幅彩色图像可以表示为一个四元数矩阵，数学表示式如公式（2）所示[5]：

对于彩色图像，fr(x,y)=0。

彩色图像f(x,y)的离散四元数傅里叶变换定义如公式（3）所示[5]：

对应的逆变换定义见如公式(4)所示[5]：

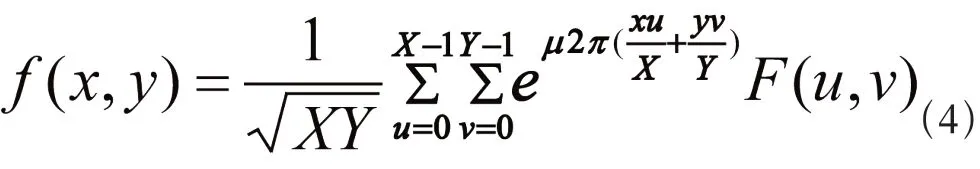
式中(x,y)和(u,v)分别为空间域和频率域的坐标。μ是一个单位纯四元数，即μ的实部为0，模为1，且μ2=-1。F(u,v)也是一四元数，可表示如公式(5)所示：F(u,v)=Fr(u,v)+Fi(u,v)i+Fj(u,v)j+Fk(u,v)k（5）包含4个分量，即Fr(u,v)、Fi(u,v)、Fj(u,v)、Fk(u,v)。

3 算法实现步骤

本算法实现步骤如下：

(1)读取原始彩色图像f(x,y)，并做四元数傅里叶变换，得到F(u,v)的4个分量；

(2)选择不同的参数，设计4个滤波器H1(u,v)、H2(u,v)、H3(u,v)、H4(u,v)；

(3)对F(u,v)的4个分量分别做滤波处理，得到滤波后的结果F'(u,v)；

(4)对F'(u,v)做四元数逆傅里叶变换，得到滤波后的图像。

4 实验结果

本实验应用MATLAB 2019a软件编程实现，原始图像选择MATLAB图像库中自带的低照度图像，实验结果如图3所示。

图3 实验结果Fig.3 Experimental results

5 结语

本文利用四元数理论，把彩色图像表示为一个四元数矩阵，整体做傅里叶变换，并设计频域滤波器，对图像做滤波处理。实验结果表明，此算法原理简单，实现方便，增强效果较好。