等梯度厚度多胞吸能结构耐撞性优化设计

张曰东，赵国辉,徐元志，张 振

(中车青岛四方机车车辆股份有限公司 国家工程研究中心,山东 青岛 266000)

列车前端吸能结构的耐撞性能是轨道车辆被动安全的主要影响因素，如何提高高速列车前端吸能结构的耐撞性能已成为目前轨道车辆被动安全研究的热点问题。薄壁结构因其低成本、高吸能效率而被广泛应用于汽车、航空、轨道交通等领域，目前薄壁结构研究的关注点在对薄壁结构的厚度和空间位置进行组合优化上[1-7]。随着变厚度板材加工工艺技术的提高，针对变厚度薄壁吸能管件的研究也逐渐兴起：文献[8]提出的超折叠单元理论指出，折角处的塑性变形能吸收大部分的冲击动能，由此可以想到将材料更多地聚集在折角区域可提升结构的吸能效率；文献[9]通过对单面和双面梯度管的耐撞性进行试验对比，认为双面梯度管的吸能效率明显强于单面梯度管，且压溃模式更为稳定；文献[10]对双面梯度厚度的方管与非凸多角管进行耐撞性仿真分析，推导出该结构的平均撞击力理论模型，认为提升厚度变化梯度可有效提升薄壁结构的吸能特性；文献[11]分别基于多项式响应面、克里金和神经网络近似模型，利用多目标遗传算法对变厚度蜂窝结构的轴向压溃进行分析，认为变厚度设计可以明显提升蜂窝结构吸能效率。

本文以某高速列车多胞吸能结构为研究对象，以截面厚度变化的梯度和截面最小厚度作为设计参数，分析不同参数下多胞结构的耐撞性能，并结合径向基函数神经网络(RBF)近似模型和NSGA- II多目标遗传算法，以最大比吸能和最小峰值力为目标进行多目标优化，得出一种最优的参数组合，以实现其最优的耐撞性能。

1 多胞管模型建立

1.1 几何模型

高速列车前端吸能结构是以八边形结构为基础、正六边形结构围绕其四周形成的五孔多胞结构，正六边形边长为56 mm；八边形侧边边长为51 mm，其余边长为56 mm。图1为多胞结构截面参数及厚度变化特征。图1中，X为胞壁截面上任意一点距离胞壁截面中间位置的长度，L为胞壁的半长度。

图1 多胞结构截面参数及厚度变化特征

为研究多胞吸能结构梯度厚度特征对吸能特性的影响，对厚度变化参数做出定义：截面中间位置的厚度为最小厚度Tmin，截面端部位置的厚度为最大厚度Tmax，厚度变化梯度S为最大厚度与最小厚度的比值，S越大说明材料越向胞壁集中位置聚集。式(1)给出了不同位置的厚度控制函数T(X)。

T(X)=Tmin+Tmin(S-1)(X/L)

(1)

1.2 有限元模型

基于有限元法对多胞管模型进行离散，网格单元类型选择4节点Belytschko-Tsay壳单元，厚度方向设置5个积分点。为模拟板材的变厚度特征，将胞壁半边长均分为8个组，每个组厚度赋值为中间位置的实际厚度。采用ANSYS/LS-DYNA软件进行多胞管轴向压溃分析，建立在压溃过程中多胞管与压块之间的主从接触和自接触模型，动摩擦因数、静摩擦因数均为0.15，压溃速度V恒定为15 m/s，压溃行程为400 mm。图2为多胞结构有限元模型。

图2 多胞结构有限元模型

多胞管结构材料为6008系铝合金[12]，其主要技术参数见表1。多胞管材料采用多线段弹塑性材料模型(24号材料)来模拟。为提升计算效率，压块材料选择刚体材料模型(20号材料)。

2 等梯度多胞吸能结构耐撞性能分析

2.1 耐撞性能评价指标

吸能结构常用的耐撞性评价的指标有吸能量EA、比吸能SEA、峰值压溃载荷PCF等。其中EA是指结构在冲击载荷下耗散的冲击能量，是瞬时压溃载荷对压溃行程的积分；SEA是指结构在压溃过程中单位质量的吸能量，其数值大小代表了吸能结构的材料利用效率；PCF是指结构在压溃过程中压溃载荷的最大值，较小的PCF能更好地保护车内乘员的生命安全。EA和SEA的数学表达式分别为式(2)和式(3)。

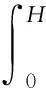
(2)

式中：H——结构最大压溃行程；

F(δ)——压溃行程为δ时的瞬时压溃载荷。

SEA=EA/M

(3)

式中：M——吸能结构的质量。

2.2 试验

试验设计提供了获取多种有效样本点的方式，主要有中心复合抽样、优化拉丁超立方抽样、哈默斯雷抽样、全因子抽样等。本文采用分布最为均匀的全因子抽样方式，等梯度多胞吸能结构的最小厚度Tmin取7个水平，设计范围为：2.8 mm≤Tmin≤4 mm；厚度变化梯度S取6个水平，设计范围为：1≤S≤2.5，共需进行42次仿真试验。

2.2.1 压溃形态对比分析

从试验管件中选取6个不同参数的试件进行试验，并对压溃形态进行对比分析。将6个试验管件分为2个对照组：CGT(2.8，1)、 CGT(2.8，1.9)和CGT(2.8，2.5)为a对照组，旨在分析厚度较薄管件的不同水平厚度变化梯度对管件压溃形态的影响；CGT(4，1)、 CGT(4，1.9)和CGT(4，2.5)为b对照组，旨在分析厚度较厚管件的不同水平厚度变化梯度对管件压溃形态的影响。CGT(2.8，1)代表最小厚度Tmin=2.8 mm、厚度变化梯度S=1的试件，其余试件命名规则相同。关于厚度变化梯度S，S=1代表低水平厚度变化梯度，S=1.9代表中水平厚度变化梯度，S=2.5代表高水平厚度变化梯度。图3为不同参数试件最终压溃变形图。

图3 不同参数试件最终压溃变形图

由图3可见，在压溃行程前段6个管件都基本能够稳定有序的压溃，但在压溃行程后段表现出差异：

(1) 在a对照组中，等厚度管件CGT(2.8，1)的压溃形态有轻微的混合模式；当S增加到1.9时，管件的压溃出现很明显的混合模式，折叠波长明显变大，压溃褶皱数量明显减少；当S增加到2.5时，压溃模式变的稳定有序，是理想的手风琴模式。

(2) 在b对照组中，等厚度管件CGT(4，1)的变形模式与a组中的类似，出现轻微的混合模式；当S增加到1.9时，管件的变形模式出现理想的手风琴模式；当S增加到2.5时，管件的压溃变形出现失稳模式，且折叠波长变大，压溃褶皱数量明显变少。

2组管件的试验结果对比发现，多胞吸能管的轴向压溃过程中，前段行程基本都能稳定有序压溃，但后段压溃行程的压溃形态有较为明显的不同。在管件厚度较薄时，中水平S管件变形出现明显的混合模式，高水平S管件则呈现理想的变形模式；在管件厚度较厚时，中水平S使管件呈现理想变形模式，高水平S管件压溃过程中则出现失稳现象。这是由于管件厚度较薄时，管件截面不同位置厚度的差异并不明显，高水平S使管件的刚度得以提高，从而使管件的吸能效率提高；管件厚度较厚时，中水平S使得管件材料的分布更为合理，从而得到理想的变形模式，但高水平S使管件不同位置截面的厚度差过大，从而导致管件的刚度严重不协调，压溃过程中出现失稳模式。

2.2.2 力学响应对比分析

对选取的6个试件的力学响应进行分析，不同试件力学响应曲线对比如图4所示。

图4 不同试件力学响应曲线对比

由图4可见，SEA和PCF的整体变化趋势是随着Tmin和S的增大而增大，且PCF在梯度恒定的情况下近似线性变化。但是在S=2.5的曲线中，当3.4 mm≤Tmin≤4 mm时，SEA和PCF的变化情况出现反常，这是由于S过大的情况下多胞管结构的刚度过于不均匀导致其在压溃过程中出现失稳，材料没有充分压溃从而出现比吸能下降的情况。可见，合理搭配多胞结构的Tmin和S可以改善其耐撞性能。

3 多胞吸能结构优化

3.1 数学模型优化

本文以多胞吸能结构的SEA最大化和PCF最小化作为优化目标，Tmin和S作为优化参数，要求吸能量EA≥初始设计吸能量E0、峰值压溃载荷PCF≤初始设计峰值压溃载荷PCF0，初始设计为厚度为5 mm的等厚度多胞管，即Tmin=5 mm，S=1。等梯度厚度的多胞吸能结构多目标优化的数学模型如下：

3.2 多目标遗传算法优化

基于RBF近似模型进行关于SEA和PCF2个响应的多目标优化，本文选用运行速度快、解集收敛性较好的多目标遗传算法中的NSGA-II算法进行优化。NSGA-II算法的参数配置为：种群规模为20，遗传代数为10，交叉概率为0.9，交叉分布指数为10，突变分布指数为20。优化出的Preto最优解集如图5所示。

图5 SEA与PCF的Preto最优解集

由图5可以看出，在SEA与PCF的Preto最优解集中，PCF随着SEA的增加而增加。理论上Preto前沿上的所有点都可以作为设计点，但高速列车多胞吸能结构的SEA直接影响列车在碰撞过程中能量耗散的大小，因此需更加关注SEA的提升。所以选取Preto最优解集中SEA最优的设计点，对应的最优参数为：Tmin=2.94 mm，S=2.46。

将优化结构与初始设计结构的仿真结果进行对比，撞击力变化曲线如图6所示。图6可以看出，优化结构的平台接触力明显提高，且PCF没有提高，表明优化结构在没有提高PCF的基础上明显提升了多胞吸能结构的吸能量。表2给出了结构优化前后的力学响应对比，从表2可以看出，优化结构的SEA提高了16.12%，PCF降低了0.39%，EA提升了18.11%，高速列车前端多胞吸能结构的耐撞性能得到了明显的提高。

图6 结构优化前后撞击力曲线

表2 结构优化前后力学响应对比

4 结束语

为提高高速列车前端多胞吸能结构的耐撞性能，本文对不同参数的等梯度厚度多胞结构进行对比分析，并基于全因子设计建立RBF模型进行多目标优化。优化后的变厚度多胞吸能结构可通过合理匹配最小厚度和厚度变化梯度，提升多胞吸能结构的耐撞性能，这一研究成果可作为高速列车吸能结构的设计参考。