基于超螺旋滑模的船载稳定平台镇定控制

刘文吉, 杜佳璐,*, 李 健, 李 诤

(1. 大连海事大学船舶电气工程学院, 辽宁 大连 116026; 2. 大连海事大学船舶与海洋工程学院, 辽宁 大连 116026)

0 引 言

作业中的船舶在风、浪等作用下产生横漂、前进、升沉、横摇、纵摇和艏摇运动,不可避免地威胁到船上设备的运行安全[1]。船舶动力定位系统可抑制船舶的横移、前进和艏摇运动[2-3],而船舶的横摇、纵摇和升沉运动需要通过船载稳定平台来隔离其对船上设备的影响,从而使船载稳定平台上支撑面相对惯性空间保持稳定,使船上设备安全平稳作业。实际中,船载稳定平台是一个具有高度非线性、强耦合、变负载的多变量系统[4-6],并遭受随机变化且不可预知的海洋环境引起的船舶摇荡运动对其产生的扰动,导致船载稳定平台运动数学模型具有动态不确定和扰动不确定,加大了船载稳定平台镇定控制难度。

自20世纪50年代至今,陀螺式稳定平台研究已相对成熟。针对舰载雷达稳定平台,文献[7]将模糊逻辑控制与传统比例-积分-微分(proportional-integral-derivative, PID)相结合,设计模糊PID控制器,较好地克服了系统非线性因素的影响。文献[8]采用灰色滑模算法设计陀螺稳定平台稳定控制器,有效减小了系统非线性摩擦扰动的影响。文献[9]和文献[10]分别根据自抗扰控制(active disturbance rejection control,ADRC)的思想设计了陀螺式平台镇定控制器,有效提高了系统的鲁棒性。然而,陀螺式平台由于其自身结构的限制,其承载能力低。

相较于陀螺式平台,并联平台具有承载能力高等优点[11-13]。文献[14]针对一个并联三自由度船载平台,根据测得的船舶横摇、纵摇和升沉运动量进行运动学反解,解算出平台每个液压缸的期望伸缩量,并设计位置PI控制器,协同控制3个液压缸,补偿船舶横摇、纵摇和升沉三自由度运动,使船载平台上支撑面保持平稳,从而隔离船舶运动对船上设备产生的扰动。针对3-SRR/SRU型并联三自由度船载平台,文献[15]在运动学反解基础上,设计了PID控制器,实现了船载平台稳定控制。文献[16]将滑模控制和PID控制相结合,为3-RPS型并联平台设计了代理滑模稳定控制器。文献[17]设计了一种3-SRR/RCR型并联三自由度船载平台及其非线性模型预测镇定控制器,仿真结果表明所设计的平台镇定控制器在控制性能和能效方面优于传统的PID控制器。针对一款Stewart结构船载平台,文献[18]提出一种基于船舶运动预报的模型预测控制策略,并通过实验验证了该控制策略的有效性及高精度。上述文献均未考虑船载稳定平台所遭受到的未知外界扰动的影响,这是不实际的。针对2UPS-RPS-PS型并联三自由度冗余驱动稳定平台,考虑稳定平台建模误差及遭受的外部干扰,文献[19]在动力学分析的基础上,提出了基于终端滑模的平台稳定控制策略,计算机数值仿真及样机物理实验验证了稳定控制策略的有效性。针对3-RRPRP/RS并联复合驱动的三自由度船载稳定平台,考虑稳定平台所遭受的内部及外部干扰,文献[20]将滑模变结构控制方法与扩张状态观测器(extended state observer,ESO)相结合,提出了基于ESO的船载平台滑模变结构镇定控制策略,计算机数值仿真及样机物理实验结果表明所提出的镇定控制策略能补偿船舶运动。针对并联三自由度船载平台,文献[21]考虑到平台横摇、纵摇、升沉运动之间存在耦合及所遭受的动态不确定与未知外界扰动,将其视为总扰动,构造ESO,实时估计这个总扰动,并设计PID反馈控制律,实现平台的稳定控制。

本文针对并联三自由度船载稳定平台(下文均简称为船载平台),同时考虑存在动态不确定以及风、浪等引起的船舶摇荡运动对船载平台造成的未知外界扰动,构造超螺旋扩张状态观测器(super-twisting extended state observer,STESO),进一步,提出基于STESO的超螺旋滑模(super-twisting sliding mode,STSM)镇定控制方案,使得船载平台上支撑面渐近调节于惯性空间中某一期望的位姿,并保持不变,使船载平台隔离船舶的橫摇、纵摇和升沉运动对船上设备运行安全的影响。

1 问题描述与预备知识

如图1所示,定义北东坐标系与船载平台上支撑面坐标系。{NE}-OneXneYneZne为北东坐标系,其坐标原点One可取为地球表面上的任何一点,OneXne轴和OneYne轴分别指正北、正东方向,OneZne轴垂直于地球表面指向下,{NE}-OneXneYneZne为惯性坐标系。{TP}-OtpXtpYtpZtp为船载平台上支撑面坐标系,将其坐标原点Otp选在上支撑面的质心,OtpXtp轴平行于船舶中线从船尾指向船艏,OtpYtp轴垂直船舶中线指向船舶右舷,OtpZtp轴垂直于OtpXtpYtp平面指向船底。平面OneXneYne与OtpXtpYtp均平行于静水面。

依据牛顿-欧拉法,建立船载平台的动力学方程[22]为

(1)

式中:p=[z,φ,θ]T为船载平台上支撑面在惯性坐标系下的位姿,由升沉位移z、橫摇角φ和纵摇角θ组成;τ=[τ1,τ2,τ3]T表示船载平台运动控制向量,τ1为升沉控制力、τ2为橫摇控制力矩、τ3为纵摇控制力矩;τd=[τd1,τd2,τd3]T表示海洋环境引起的船舶运动对船载平台的扰动,τd1为升沉扰动力、τd2为橫摇扰动力矩、τd3为纵摇扰动力矩;M(p)∈R3×3为惯性矩阵,其表达式为

(2)

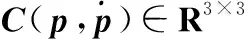
(3)

G=[mpg,0,0]T为重力向量,g为重力加速度。

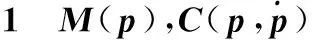
假设 2风、浪等海洋环境引起的船舶运动对船载平台的扰动τd是未知时变的,τd,i(i=1,2,3)及其变化率是有界的。

其中,船载平台的动态模型参数难以精确获得;另外风、浪等对船舶运动的干扰具有明显的随机性,且预先是不可知的,但其所具有的能量有限。因此,假设1与假设2合理。

控制目标:在假设1与假设2的条件下,设计船载平台镇定控制律,使得船载平台上支撑面保持在惯性坐标系中某一期望的位姿pd=[zd,φd,θd]T不变。

引理 1[23]考虑系统:

(4)

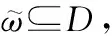
(5)

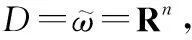
(6)

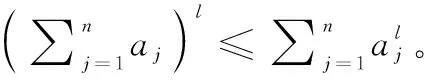
2 船载平台镇定控制律设计与稳定性分析

本节首先设计STESO,为船载平台的总扰动提供在线估计,分析STESO的收敛性;基于此,利用超螺旋算法设计船载平台有限时间镇定控制律,并进行系统稳定性分析。

2.1 STESO设计

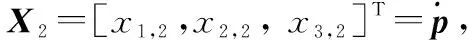
(7)

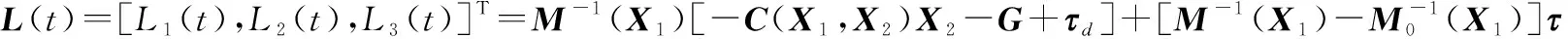
针对式(7),设计如下滑模面:

S=ε2+λε1

(8)

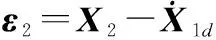
将滑模面S对时间求导,根据式(7),可得

(9)

将船载平台的总扰动L(t)扩张为一个新的状态向量N(t)=[N1(t),N2(t),N3(t)]T,得到如下增广系统:

(10)

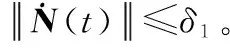
记

(11)

针对增广系统式(10),构造如下形式的STESO:

(12)

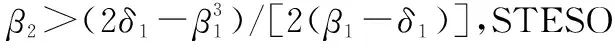
证明定义STESO的估计误差:

(13)

将式(13)对时间求导,根据式(10)和式(12),可得STESO的误差动态方程:

(14)

(15)

将η1对时间求导,根据式(14),可得

(16)

将η2对时间求导,根据式(14),可得

(17)

将η(t)对时间求导,根据式(16)与式(17),可得

(18)

式中:

针对STESO的误差动态方程式(14),构造如下李雅普诺夫预选函数:

V1(η(t))=η(t)TP1η(t)

(19)

式中:

将式(19)对时间求导,根据式(18)可得

(20)

式中:

(21)

根据完全平方不等式与式(21),可以得到

(22)

式中:

将式(22)代入式(20)中,可得

(23)

式中:

设计参数β1与β2满足:

β1>2δ1

(24)

(25)

根据式(15)、式(19)以及式(21),有

(26)

将式(26)代入式(23)中可得

(27)

式中:

由引理1和式(27)可知,η(t)会在有限时间

(28)

证毕

2.2 船载平台STSM镇定控制律设计

基于所构造的STESO式(12),利用超螺旋算法,设计船载平台STSM镇定控制律:

(29)

式中:α1>0与α2>0为设计参数。

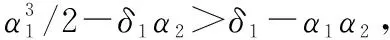
证明将控制律式(29)代入式(9)可得

(30)

(31)

将η′(t)对时间求导,根据式(30),可得

ω1=diag(|S1|-1/2,|S2|-1/2, |S3|-1/2)

针对由式(1)、式(12)和式(29)构成的船载平台闭环控制系统,构造如下李雅普诺夫预选函数:

V2(η′(t))=η′(t)TP2η′(t)+V1(η(t))

(33)

式中:

将式(33)对时间求导,根据式(28)与式(32),可得

(34)

式中:

(35)

根据完全平方不等式与式(35),可以得到

(36)

式中:

将式(36)代入式(34)中,可得

(37)

式中:

如果设计参数α1与α2满足

α1>2δ1

(38)

(39)

(40)

将式(40)代入式(37),并根据引理2,可得

(41)

式中:

根据引理1和式(41)可知,η′(t)在有限时间

(42)

内收敛到零,则滑模面S在有限时间ts2内收敛于零。进一步,根据式(8),船载平台镇定误差ε1与ε2渐近收敛于零。

证毕

3 仿真研究

为验证所设计的船载平台STSM镇定控制律的有效性,以某一船载平台为例进行仿真研究,其动力学方程式(1)中的模型参数标称值为mp=300 kg、Ix=10.59 kg·m2、Iy=10.59 kg·m2、Iz=19.85 kg·m2[21]。进一步,将所设计的船载平台STSM镇定控制律与基于ADRC的船载平台镇定控制律进行仿真比较,以表明所设计的船载平台STSM镇定控制律的优越性。

3.1 船载平台STSM镇定控制律仿真

本节利用Fossen[25]和Perez研制的MSS(Marine Systems Simulator)软件包,获得海浪引起的船舶运动对船载平台的扰动力及力矩,分别在两种海况下对所提出船载平台STSM镇定控制律进行仿真实验。

分别在2级和4级海况下进行仿真。仿真中采用ITTC(International Towing Tank Conference)双参数海浪谱,2级海况参数选择为波浪扩散因子数值为2、平均波向为30°、有义波高为0.5 m;4级海况参数选择为波浪扩散因子数值为3、平均波向为120°、有义波高为2.5 m。不施加控制作用情况下的船载平台上支撑面位姿运动仿真曲线如图2所示。

(1) 2级海况下船载平台动力学方程式(1)的惯性矩阵取其标称值,即M(X1)=M0(X1)。

仿真中,设船载平台上支撑面的期望位姿X1d=[0 m,0°,0°]T,船载平台上支撑面的初始状态为X1(0)=[0.1 m,1°,2°]T和X2(0)=[0 m/s,0°/s, 0°/s]T;选取所构造的STESO的设计参数为λ=1,β1=3,β2=20,所设计的STSM镇定控制律的参数为α1=4,α2=0.3,仿真结果如图3～图5中实线所示。图3为船载平台上支撑面在升沉、橫摇和纵摇方向上的运动曲线,由图3可知,所设计的船载平台STSM镇定控制律能控制船载平台有效隔离船舶的横摇、纵摇和升沉运动对船上设备运行安全的影响,保证船载平台的上支撑面始终保持期望的位姿。图4为船载平台上支撑面升沉控制力以及横摇、纵摇控制力矩曲线,由图4可知,控制力及力矩是合理的。图5为船载平台的总扰动及其估计曲线,由图5可知,所构造的STESO可以提供对总扰动的估计。

(2) 4级海况下船载平台动力学方程式(1)的惯性矩阵摄动为M(X1)=(1+30%)M0(X1)。

仿真中,设船载平台上支撑面的初始状态、期望位姿、STESO和STSM镇定控制律的设计参数均与2级海况下的一样,这意味着在不同海洋环境扰动下,船载平台镇定控制律保持不变,仿真结果如图6～图8中实线所示。由图3～图5与图6～图8可知,在海洋环境扰动变大且存在模型参数摄动时,所设计的船载平台STSM镇定控制律展现了与2级海况下几乎同样的控制效果,这表明所设计的船载平台STSM镇定控制律对模型参数摄动和未知外界扰动具有良好的自适应能力和鲁棒性。

3.2 仿真比较

本节中,将所设计的船载平台STSM镇定控制律与文献[21]中的船载平台ADRC镇定控制律式(43)和式(44)进行仿真比较。

(43)

(44)

式中:i=1,2,3。

取设计参数b0,1=300,ωo,1=13,kp1=12,kd1=20;b0,2=13,ωo,2=13,kp2=14,kd2=48;b0,3=14,ωo,3=13,kp3=15,kd3=50,分别在第3.1节中的两种情况下对船载平台ADRC镇定控制律进行仿真,仿真结果见图3～图8中点线。由图3和图4可知,在2级海况下,船载平台ADRC镇定控制律和本文所提的船载稳定平台STSM镇定控制律均具有同样令人满意的控制性能。但由图6和图7可知,在4级海况下,本文所提出的船载平台STSM镇定控制律的镇定误差较小。另一方面,由图5和图8可知,两种情况下,所设计的STESO相较文献[21]中的船载平台构造的常规ESO的估计精度都高。上述仿真结果充分表明了本文设计的基于STESO的船载平台STSM镇定控制律较船载平台ADRC镇定控制律的优越性。

4 结 论

本文针对船载平台存在的动态不确定以及未知外界扰动,构造了STESO,估计由动态不确定以及未知外界扰动引起的总扰动;进一步,设计了船载平台STSM镇定控制律,理论分析及仿真结果均证明了所设计的控制律可使船载平台上支撑面保持在惯性空间中某一期望的位姿不变,且较船载平台ADRC镇定控制律控制精度高,可隔离船舶运动对船上设备运行安全的影响,从而可提高船上设备在不同海洋环境条件下的可操作性和安全性。