基于分布式协同进化的星座自主任务规划算法
高天旸, 胡笑旋, 夏 维
(1. 合肥工业大学管理学院, 安徽 合肥 230009; 2. 过程优化与智能决策教育部重点实验室, 安徽 合肥 230009)
0 引 言
对地观测卫星,即遥感卫星,是一种广泛应用于地面勘探、环境监测、气象预测、军事侦查等重要领域的战略资源。在传统遥感卫星系统应用过程中,卫星任务规划通常在地面进行,在应对突发需求时制定的新方案往往需要等待下一次卫星过境测控站才能上注执行,这极大地限制了遥感卫星系统的响应速度[1-2]。随着星载计算能力的提升,卫星任务规划自主化成为了可能,自主化即减弱卫星运行对地面系统的依赖,将任务规划运算交由星载芯片进行,能一定程度摆脱测控可见性的限制[3-4]。当前,遥感卫星系统不断由多星向星群、星座发展,其星间协作关系愈加密切,星座协同自主任务规划逐渐成为自主化卫星管理与控制方法的主要发展方向[5]。
星座协同自主任务规划旨在为不同物理结构的星座系统设计采用不同组织结构的协同策略与相应的优化算法,从而令星座内各星互相协同合作以共同制订整体任务执行方案。自主协同星座的组织结构主要可分为全集中式、集中协调式、并行集中式(部分分布式)与全分布式4类,其中前三者可以被归纳为层级化结构[6]。文献[7-8]面向主从结构星座系统,设计了一种全集中式混合动态变异遗传算法与两种重规划方法,其方案由主星规划形成并分发至各从星执行。文献[9]提出了一种集中协调式规划策略,先由主星将任务信息广播至各从星,各从星评估自身观测能力与成本形成报告返还主星,最终由主星选定各任务执行星。文献[10]提出了一种多维多智能体协作模型,主星使用基于合同网协议的分配方法,通过公告、招标、授予等步骤对各从星进行任务分配与重分配。在层级化结构中,各星被分为主星与从星两种角色,主星负责对系统进行统筹规划并主持星间协调过程,从星被动地接收来自主星的筹划结果、进行自我方案规划并参与协调过程。采用层级化结构的方法具有清晰的规划流程,能快速形成有效方案,但由于其流程围绕主星节点开展,对其的计算能力与通信环境的要求较高,因此主要应用于拥有高算力节点或稳定通信总线的星座系统。
在采用层级化结构的自主星座中,当主星遭遇意外而失效时,整个系统将陷入瘫痪,而采用全分布式结构则可避免此类问题。文献[11-12]将主星损坏后星座内剩余各从星看作多个互相通信与协商的独立智能体,并分别对其效用函数进行识别,提出了基于效用的后悔博弈、烟雾信号博弈和基于广播的博弈作为分布式协商策略,并改进混合动态变异遗传算法以使其适用于分布式优化环境。文献[13]设计了一种多星智能体协调协商任务分配算法,率先收到任务信息的卫星向其所有邻近星广播以构成群组,群组内各星首先评估自身对各任务的执行意向,随后共同进入一种基于最大增益信息算法的分布式协调迭代优化过程以形成最终分配方案。文献[14-15]提出了一种基于任务联盟构建的星间协作方法,各星智能体通过基于信任度的知识传播策略以不断传递已知任务信息与他星执行意向信息,并据此改进自身意向以优化整体任务分配方案。在全分布式结构中,各星作为平等个体共同参与协调优化过程,通过积极的通信交互以对任务分配进行协调并生成相应的执行方案。采用全分布式结构的方法可利用不同星间的通信能力组成信息网络以支持其协调过程,从而使各星承担的通信与计算压力更加平均,适用于不具备强算力节点或星间通信能力不稳定的星座系统。
基于上述分析,本文进一步探究全分布式结构方法对各星计算资源的运用方式,提出了一种全分布式星座协同迭代优化策略,将制定多星整体方案的总问题转换为多个制订单星方案的分问题。在该策略中,各星被看作为独立智能体,通过“接收”“更新”“发布”的三阶段协作行为在相应分问题解空间中探索总问题的优质解。在此基础上,本文设计了一种分布式多智能体合作式协同进化遗传算法,该算法对不同卫星方案进行编码形成多个亚种群,利用不同自主卫星的计算资源实现各亚种群并行进化,并通过各亚种群特征信息的传播与接受过程来协调任务在各星间的分配。同时,设计了一种包含时间窗间重叠度因素与自适应机制的适应度函数,能够有效引导各亚种群共同朝着提升整体方案质量的方向进化,进一步增强算法的寻优能力。最后,本文在S698PM嵌入式开发环境下进行仿真实验,结果表明,所提出方法在小规模问题中能求得与CPLEX效果相当的优质解,在大规模问题中表现出比贪婪算法与集中式遗传算法更强的优化能力,同时在恶劣通信环境下展现出良好的适应性,适用于不同拓扑结构的星座系统。
1 问题描述
在一个由多颗自主遥感卫星组成的星座系统中,各星除了基本的观测与通信能力外,还都拥有一定的星载算力,且具有计算任务目标访问时间窗的功能。如图1所示,当一批待观测任务集合信息以地面上注或星上自生成等方式到达星座中任一卫星,该星作为规划发起星,需要调动星座内的其他卫星与其共同针对该任务集合进行分配与规划,以求整体方案中的被执行的任务权重的总和最大。该任务集合中包含一定数量的地面点目标,对其中任一目标的观测都需要占用一颗遥感卫星的一段工作时间,且执行时间段必须在该卫星对目标的可见时间窗内。
1.1 概念定义
(1) 任务:T={t1,t2,…,ti,…,tNT}表示一批刚到达的待规划任务集合,NT为集合中任务的数量,其中每一个任务ti可以通过一个二元组ti=(tvi,di)表示,i为任务序号,tvi表示该任务的权重,di表示该任务所需观测持续时间。
(2) 卫星:S={s1,s2,…,sj,…,sNS}表示星座系统中所有卫星的集合,NS为集合中卫星的数量。
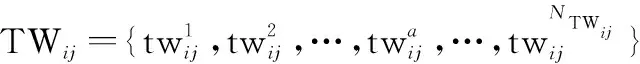
1.2 多星任务规划问题模型
根据上述定义对星座内的多星任务规划问题进行建模,可得模型如下:
(1) 决策变量
(2) 目标函数
在系统整体执行方案中所有被安排执行的任务的总权重之和最大。
(1)
(3) 约束条件
(2)
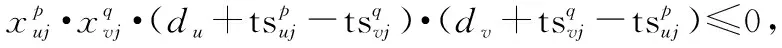
(3)
(4)
其中,式(2)表示每个观测任务最多只能被执行一次;式(3)表示同一卫星对先后两个任务的观测持续时间不能有重叠;式(4)表示每个任务执行持续时间必须在其可见时间窗内。
1.3 全分布式环境下单星规划分问题
在全分布式环境下,受限于全局信息(他星任务可见性与初始执行状态)的缺失,单星智能体在协调优化过程中对星座内多星任务规划问题的探索能力仅限于对自身规划方案进行调整。如图2所示,将制定多星整体方案的总问题转化为多个制订单星方案的分问题并分别交由对应各星智能体进行独立探索。各分问题模型仅包含与本星方案相关的决策变量,其余变量则通过读取他星方案作为已知常量输入,而目标函数与约束条件则与总问题相同。将各分问题的解组合即可形成总问题的解,各星通过探索不同的单星方案组合以对整体方案进行寻优。
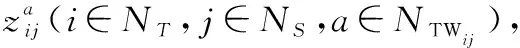
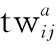
(5)
(6)
2 分布式协同规划算法
针对上述遥感星座自主协同任务规划问题,本文设计了一整套的全分布式协同优化策略与相应规划算法,本节将对其进行具体描述。
2.1 全分布式星座协同迭代优化策略
受启发于文献[19]中描述的分布式多智能体组合优化启发式(combinatorial optimization heuristic for distributed agents, COHDA)算法,本文设计了一种基于“接收”“更新”“发布”的三阶段协作行为的全分布式星座协同迭代优化策略,如图3所示。
其主要流程如下。
步骤1发起星将任务集合信息广播至星座内其余各星,各星随即针对任务集合进行自我规划形成本星初始方案并储存至本星方案集,系统进入方案优化阶段。
步骤2在方案优化阶段中,各星不断循环进行以下三阶段行为:① 向星座内其余各星发送本星方案集中的方案;② 将从他星接受到的最新方案储存至本星方案集;③ 根据方案集中的他星最新方案优化更新自身方案并储存至本星方案集,随后返回阶段①。
步骤3当到达预设的运行时限后,方案优化阶段结束,此时各星上储存的方案集内容均相同,都包含各星最新提出的本星方案,但不同星方案之间仍可能存在重复执行冲突;各星对其进行规则统一的冲突消解后形成最终整体方案。
2.2 多智能体合作式协同进化遗传算法
基于上述全分布式星座协同迭代优化策略,本文设计了一种多智能体合作式协同进化遗传算法(distributed agent-collaborative coevolution genetic algorithm,DA-CCGA),CCGA[20]是传统遗传算法的变体,其使用多个并行进化的亚种群将对复杂问题的优化搜索过程分解为对多个较简单的分问题并行搜索,具有对分布式计算环境的先天适应性[21]。DA-CCGA由CCGA融合上述全分布式优化策略而形成,令代表不同星方案的亚种群分布于相应星上,各星亚种群相对独立地进化以探索本星方案分问题,并通过交换种群特征信息以辅助适应度评价过程。DA-CCGA如算法1所示。

算法1 DA-CCGA输入:卫星集合S;本星编号sid;待规划元任务集合T;待规划任务的本星时间窗集合TWsid;传播周期Pspread;规划运行时限Ptmax输出:最终整体规划方案P*1初始化最优印象集I*sid与抽样印象集Isamsid2初始化本星初始亚种群P0sid←init(TWsid)3计算初始亚种群适应度estimate(P0sid,I*sid,Isamsid)4向他星传播印象集spread(P0sid,I*sid,Isamsid)5初始化代数计数g←16 While 当前运行耗时pt
(1) 染色体编码与解码
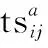
(2) 印象集
非小细胞肺癌表皮生长因子受体基因突变274例分析…………………………………………………… 王 艳等(20):2817
在DA-CCGA中,各星储存的方案集被扩充为“印象集”,即本星记录的对他星亚种群特征个体的印象,包括“最优印象集”,即已知最新的各亚种群最优方案个体集合,与“抽样印象集”,即已知最新的从各亚种群随机抽取的方案个体集合。印象集中的所有方案个体均依据“最后更新时间戳”进行管理。各星通过不断地传播、接收、更新再传播印象集信息,以满足各亚种群在进行适应度评价时对他星方案信息的需求。
(3) 适应度函数
如图5所示,各星亚种群中单条染色体的适应度值为其与他星染色体组成的整体方案的计算值,计算函数如下:
(7)
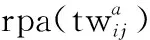
(4) 适应度评价过程
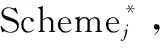
(8)

(5) 亚种群协作策略
如图6所示,传播种群特征即向所有邻近星发送本星储存的印象集信息,在每次发送前需要随机从本星亚种群中抽取的一个方案个体以更新本星抽样印象集。而接受种群特征即接收来自他星的印象集信息并根据其时间戳更新本星印象集,若接收后本星印象集发生变化则需重新计算本星亚种群内所有个体的适应度。
(6) 交叉与变异
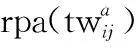
如图8所示,变异算子随机作用于染色体的某个基因位上,将该基因位的执行任务去除后尝试重新插入除任务以外的任务后得到变异后的染色体。
(7) 最终整体方案提取
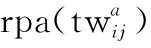
3 仿真实验分析
为了验证本文所提出的方法的适用性与有效性,本节使用S698PM嵌入式开发环境模拟星座系统中分布式星载算力以对其自主任务规划过程进行仿真实验,该星座由5颗自主遥感卫星组成,其中2颗为中轨卫星,其余3颗为低轨。实验模拟五星星座在一定规划运行时限内对一定规模任务集合在特定规划时域内的方案进行自主规划,规划使用的任务点目标坐标数据为随机生成,其可见时间窗数据由仿真软件模拟计算。
3.1 参数与通信环境敏感性测试
为了测试部分重要参数与星间通信环境变化对于DA-CCGA效能的影响,使用相应不同设置的多组实验进行对比分析,每组重复运行50次并计算平均目标函数值,在测试中,待规划任务数量为1 000,规划时域长度为12 h,规划运行时限为30 min(1 800 s)。
(1) 传播周期影响
在DA-CCGA中,由于各亚种群的适应度评价过程依赖于对其他亚种群特征信息的获取,故各卫星在优化过程中进行种群特征传播的频率变化必然会对算法效能造成影响,为探究其具体影响模式,设置不同传播周期时长的实验组进行对比,最终结果如图10所示。
可见,传播周期变化对算法效能的影响并非是单向的,过短或过长的传播周期均会降低算法的寻优能力与稳定性,这通常是因为过于频繁的传播与接收将导致各星反复对亚种群进行重新评估,在大量占用计算资源的同时过度限制各亚种群的搜索方向,妨碍了搜索过程的有效进行。当传播周期适中(15~20 s)时算法优化效能达到峰值,此时各星在整个规划过程中可向他星传播种群特征信息89~119次。随后继续增加传播周期至450 s(传播4次),算法仍能以良好的稳定性得到满意解(与峰值的平均差距小于1.1%),但当传播周期增加至600 s(传播2次)以上时,在寻优能力降低的同时算法的稳定性也受到显著影响。可见DA-CCGA能以较低的星间通信频率到达接近高频率的效果,对恶劣的星间通信环境具有良好的适应性,但仍需要一定次数的星间通信以支持其各亚种群的有效进化。
(2) 启发式因子影响
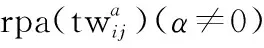
(3) 星间拓扑与通信能力影响
在现实应用环境中,不同星座系统在不同时刻可能拥有不同的星间拓扑结构与相应的通信能力,为了检验DA-CCGA对不同通信环境的适应能力,设置以下通信拓扑场景,所有场景时长均为30 min:
① 稳定通信环境场景
S:其中一星与其他所有星之间可以稳定互相通信,其余星之间无法通信,即星形拓扑结构;
C:所有卫星均可以稳定与左右两邻星互相通信通信以组成环形拓扑结构;
L:去除环形拓扑中某两星的相互通信能力以形成线形拓扑结构;
A:所有卫星均可以稳定与任意另一星互相通信的网状拓扑结构。
② 不稳定通信环境场景
M:由仿真软件模拟计算出2021年1月18日18:00至2021年1月18日18:30时间段内各星间真实可见性组成的不稳定通信环境场景;
S30-A30:场景开始后的30 s内为“S”,场景结束前的30 s内为“A”,其余时间任意两星间均无法通信;
S1-A30:场景开始后的1 s内为“S”,场景结束前的30 s内为“A”,其余时间任意两星间均无法通信。
使用以上通信环境设置不同实验组进行对比,最终结果如图12所示。
如图12(a)所示,在稳定通信环境场景中,不同星间拓扑结构实验组的结果均十分相似,其中A与C拓扑结构略优,S与L拓扑结构稍次之,可见DA-CCGA对不同拓扑结构的星座具有较强的适用性,但通信机会在星座内分布较为广泛且平均的拓扑结构依然能对算法效能产生正向的影响。
如图12(b)所示,DA-CCGA在M中的表现与其在稳定通信环境场景各实验组中的非常接近,这再一次验证了DA-CCG对恶劣的星间通信环境的适应性。而S30-A30与S1-A30均为仅允许卫星在规划运行开始后与结束前的小段时间内进行通信的极端恶劣通信环境场景,但对算法性能的影响却有巨大差距。算法在S30-A30中的表现仅略逊于各稳定通信环境场景与M(差距在0.4%以内),而S1-A30的结果却与M拥有4.98%的差距,由此可见DA-CCGA适应恶劣通信环境的前提是:各星在优化搜索过程的初期拥有足够的通信机会以充分了解他星初始亚种群的种群特征,从而有效指导本星亚种群在整个运行过程中的进化。
3.2 对比实验
DA-CCGA作为一种全分布式搜索算法,可充分地利用分布于星座内的计算资源以不断对问题进行寻优,但同时其搜索优化过程却依赖于各节点间的通信协调。为了具体对比DA-CCGA与传统集中式方法的寻优能力,设置了多组不同问题规模的实验组,分别使用贪婪插入(greedy insert, GI)算法、集中式遗传算法(centralized genetic algorithm,CGA)与DA-CCGA进行优化求解,同时将第1.2节中描述的多星任务规划模型线性化后使用CPLEX尝试求其精确解与上述算法优化结果进行对比,其中CGA仅使用单颗模拟卫星算力运行,CGA与DA-CCGA均重复运行50次并计算平均目标函数值,最终结果如表1所示。表1中“—”表示无法求解;规划运行时限仅针对CGA与DA-CCGA,而CPLEX运行耗时并未给出。

表1 算法对比测试结果
当问题规模较小(任务量小于等于250)时,GI、CGA与DA-CCGA均能以较短的运行时间得出与CPLEX精确解相同或相近的结果,当问题规模扩大(任务量大于250)时,CPLEX由于模型约束数量限制被超过而无法求解,而CI、CGA与DA-CCGA之间的差距逐渐扩大,且DA-CCGA一直具有明显的优势。以1 000任务数测试组为例,如图13所示,从单次运行结果的分布区间来看,DA-CCGA的稳定性略优于CGA,两者的寻优效率都随着运行时间的延长而减缓,但DA-CCGA的减缓速度明显低于CGA,当到达25 min时,CGA已趋于收敛,而DA-CCGA则仍具有可继续优化的趋势。最终DA-CCGA搜索到的最优解目标函数值平均比CGA高出2.85%。可见,DA-CCGA对于星座任务规划问题,特别是大规模问题,具有相较于传统集中式方法更强的优化搜索能力。
4 结 论


