利用复摆测量重力加速度及对摆的位形参数的测量

隋林泓 刘利霜 赵鑫雨 曹彦煜 贾春硕 李喜彬

（内蒙古师范大学物理与电子信息学院 内蒙古 呼和浩特 010022）

重力加速度在工程物理的各个领域中都扮演着重要的角色，因此，精确地测量当地的重力加速度一直是工程物理实践中的一项重要任务.对重力加速度的测量方法有很多，比如单摆法［1］，悬挂弹簧法［2］，当然最简单的办法是在小球上贴一个加速度传感器.不过以上方法只能实现一次测量，无法给出不同物理量下的实验数据，这就增大了实验的偶然误差.本实验最大的亮点在于可以通过悬挂不同质量磁铁的方法，获得多组数据，并利用回归分析的方法，有效地降低了偶然实验误差，从而提高了实验精度.

1 实验目的

对当地重力加速度进行精确地测量，以及对钢尺不规则部分有效长度的测量.

2 实验器材（含规格）及成本

硬件：钢尺（5 cm）、钕铁硼磁铁10块（40 m m×20 m m×5 m m）、游标卡尺、天平、长尾夹、MR63ZZ微型轴承（Dφ6 m m×dφ3 m m×B2.5 m m）、智能手机、计算机.

软件：phyphox，M ATLAB R2019，Anaconda3，Adobe illustrator CC2019.

成本：10块钕铁硼磁铁约40元，50 cm钢尺10元，轴承1.5元，其余物品仪器均可在实验室或者日常生活中找到，总成本约50元.

说明：这里没有用到复摆支架，是因为实验过程中要在钢尺的一端吸附上磁铁，而复摆的支架同样为铁质，会对实验产生非常大的影响.

3 实验原理

实验装置的原理图如图1所示，O点为旋转中心.旋转中心到下边缘的距离为l1，其分布的质量为m1，剩余的质量为m2.钢尺总质量M=m1+m2，下端磁铁质量为m.由于上端的质量分布不是规则的，这里设有效长度为l2，即质量为m2的物质分布在长度l2上，而且这个长度可以通过本实验测量得到.

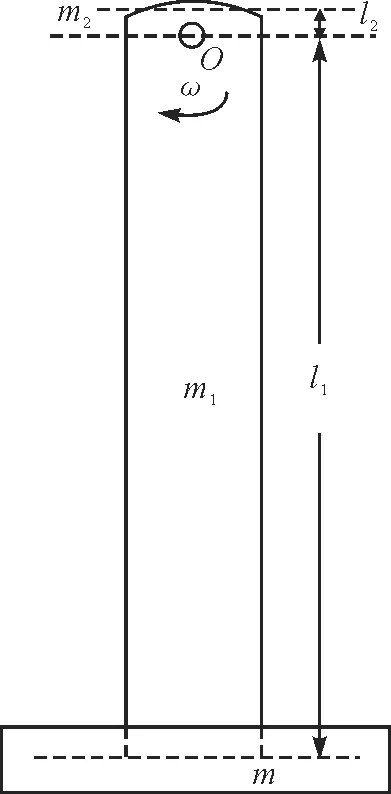
图1 实验装置原理示意图

由上面的讨论可以得到如下关系.

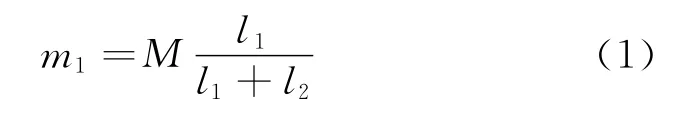
设系统转动惯量为I，由刚体定轴转动定律

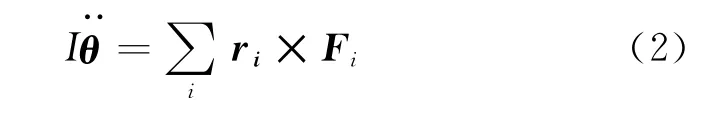
得到系统的运动方程为

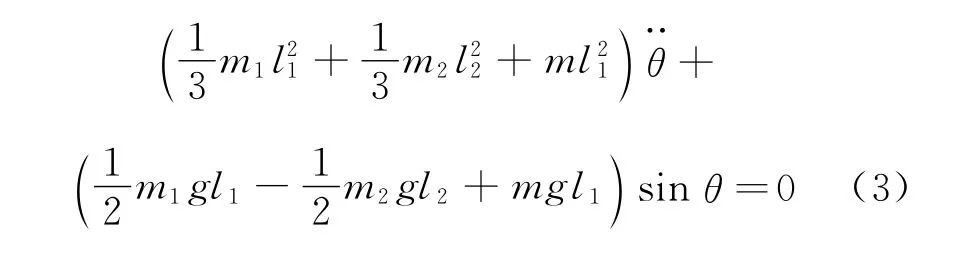
在小摆角条件下，式（3）可以近似为

可对上式中的角频率作进一步的处理

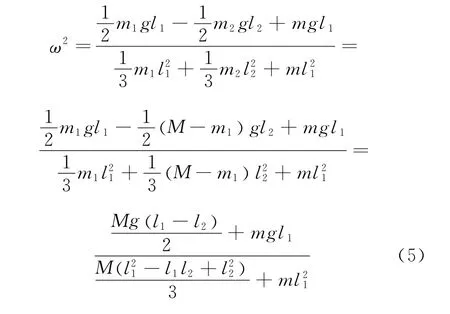
这里用到了式（1）.在式（5）的分母上，虽然l2要比l1小很多，但为了保证实验的精度，这里保留关于l2的一阶项，但忽略l2的二阶项，并定义有效质量

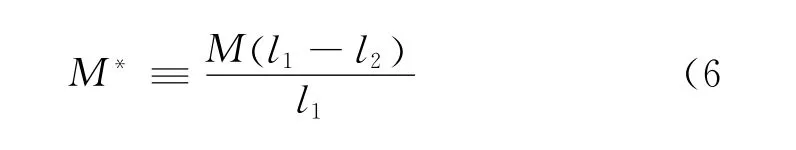
于是，式（5）中的角频率就可以写为

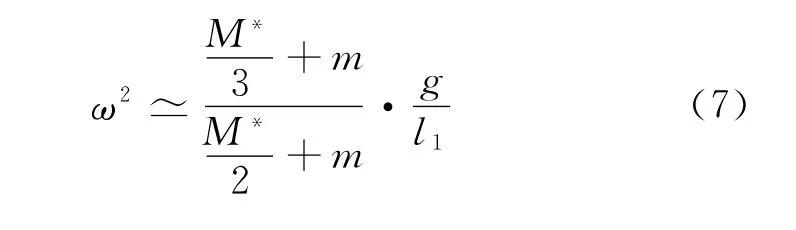
复摆往复运动的周期就可以写为

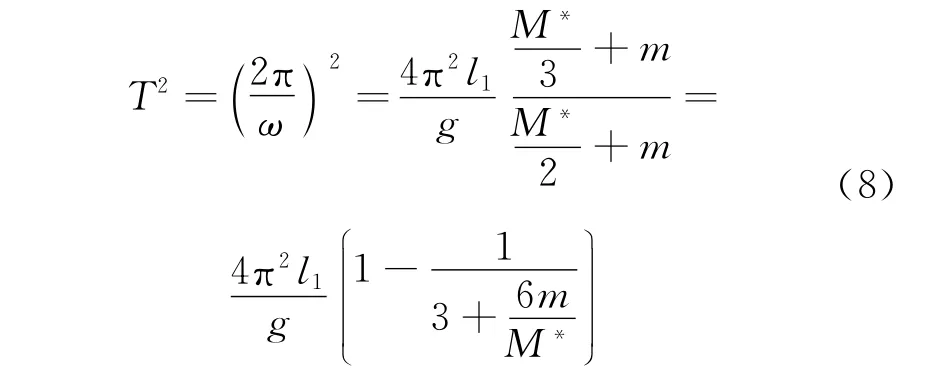
在实验原理上，本实验有如下优势.第一，对实验装置进行了尽可能详细的理论计算，并分析了它对实验结果带来的影响.第二，通过在钢尺末端吸附不同质量的磁铁，即改变变量m来得到不同情况下的运动周期，从而排除了偶然误差对实验结果的影响.第三，所需测量的物理量，包括摆长l1、摆锤运动周期T以及悬挂磁铁的质量m，都可以进行精确地测量，相对误差均远小于.最后，可以通过非线性回归分析得到钢尺的有效质量，从而确定有效位形参数l2.

4 实验方法

原理图图1所对应的实物图如图2所示，前文已经明确说过，实验中不应该使用复摆架，这里只需放在一个比较空旷的位置即可.

图2 原理图1所对应的实物图

具体的实验步骤如下.

（1）用游标卡尺测量50 cm处到圆孔上端的距离，如图3所示，读数为23.80 m m，钢尺小孔直径6.20 m m.则50 cm处到旋转中心的距离l1为读数减去轴承外直径的一半，即l1=0.520 7 m.

图3 钢尺刻度50 cm处到小孔远端的距离读数

（2）取一个长尾夹的手柄并在末端反复缠绕透明胶带，直到使得轴承恰好卡在上面不发生滑动.在轴承的外侧缠上双面夹带，使得恰好嵌入在钢尺的圆形切口处，并使之不发生相对滑动.用长尾夹将上面的装置夹在空旷的位置，比如桌角处.

说明：使用轴承有以下几个好处.第一，如果将钢尺直接悬挂在悬针上，钢尺会发生纵向滑动，这会严重地增加实验误差.第二，减小了摩擦力.第三，补偿在钢尺圆环处质量的缺失.

（3）用天平测量需要吸附在钢尺上磁铁的质量.

（4）将安装有phyphox应用程序的智能手机放在装置下方约10 cm处，将需要进行实验的磁铁吸附在钢尺末端，并调整位置，使得磁铁的上边缘恰好和钢尺上的1 cm刻度重合，这样磁铁重心刚好落在了钢尺的末端.

（5）给钢尺一个合适的初始摆角（小于5°）并无初速度释放.运行phyphox应用程序的磁力计并记录数据，一组记录时长约65 s，保存数据并导入计算机.同样的方法共记录11组数据.

（6）数据分析.

5 数据处理与分析

5.1 数据处理

数据显示，复摆的运动具有很好的周期性，phyphox应用程序记录的周期性磁场如图4所示.

将保存好的Excel文件由M ATLAB读取、画图.打开图片，找到图像相对稳定的一段（一般在25 s之后），选择一个峰并放大直到可以看清最大值所在的位置，单击该点，此时会显示最大值处的坐标，横坐标即为该峰顶点所在的时间坐标.再缩小，选择和此峰间隔数为10的另外一个峰.重复上面的放大操作，得到这个峰的坐标.那么复摆的运动周期就是

图5是悬挂质量为26.0 g的数据获取示意图，数据可以精确到10-5s.

图5 获取复摆周期的方法示意图

重复这个步骤，可获得其他10组实验的数据，其详细的结果展示在表1中.

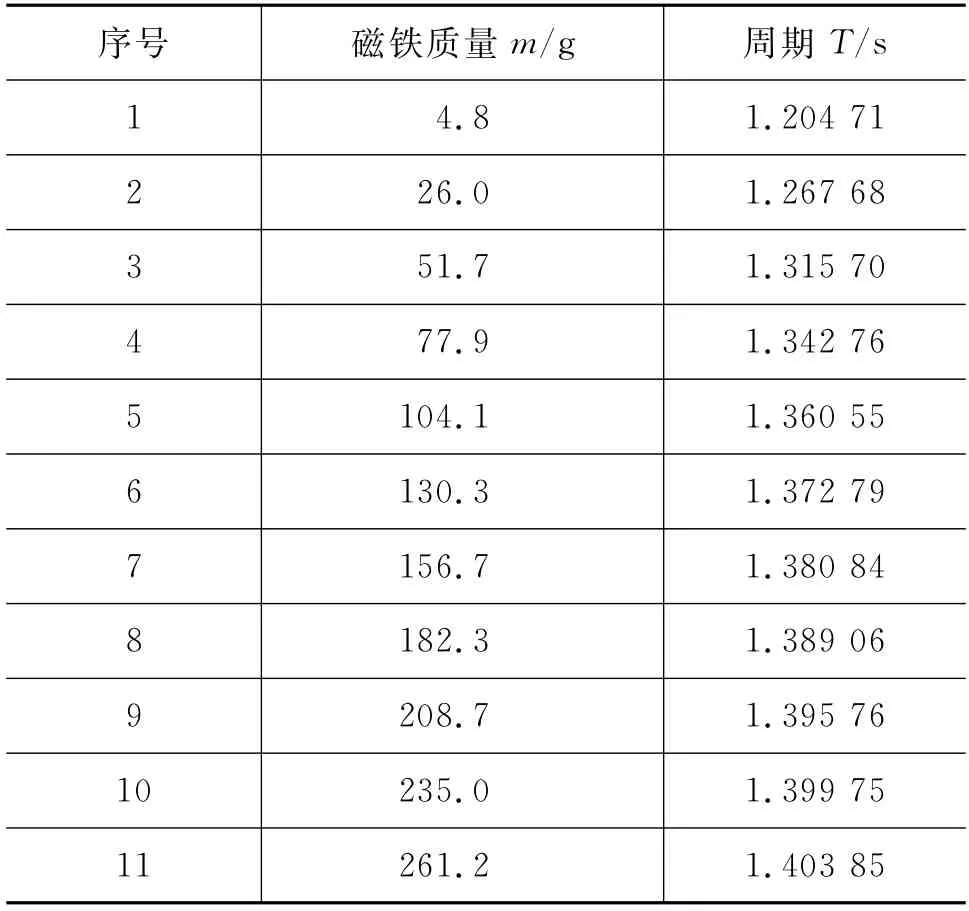
表1 悬挂磁铁质量与周期的实验数据

5.2 非线性回归分析

针对表1获得的测量数据，采用式（8）定义的回归函数，计算过程中利用M ATLAB软件自带的Non Linear Model.fit函数，最终得到最佳拟合结果是：重力加速度估计的中心值为g=9.803 9 m／s2，置信度为0.95的置信区间为（9.803 9±0.023 006）m／s2，误差为0.054%（当地标准重力加速度为g标准=9.798 64 m／s2），有效质量估计的中心值为M*=114.79 g，0.95的置信区间为（114.79±3.617 9）g.同样利用方差传递公式，得到有效位形参数的中心值为=6.760 6 m m（M=116.3 g），置信区间为（6.760 6±0.0162 4）m m.利用python软件绘制出T2-m的数据点及拟合函数并带有误差棒，如图6所示.

图6 实验数据的回归分析图

6 误差分析

在之前的讨论中可知，为了确定重力加速度需要测量如下几个物理量：旋转中心到钢尺零刻度的距离，这是误差最大的来源，首先旋转中心到50 cm刻度处的距离测量误差会比较大，但不会超过1 m m；磁铁的宽度并没有达到20 m m，事实上只有约19.6 m m，因此在磁铁上端与钢尺的10 m m处重合的同时，磁铁的重心并未与钢尺的零刻度处重合，但误差不会超过0.3 m m，总体而言旋转中心到钢尺的零刻度的距离误差大约在1 m m左右.利用天平测量钕铁硼磁铁的质量时，系统误差为0.1 g，但随着磁铁数量的增加，这个相对误差会越来越小.振动周期利用相关软件获得，精度为10-4s，虽然有人为的误差，但只要做到精细，这个误差可以维持在10-4s.利用前面的计算，重力加速度可以写为

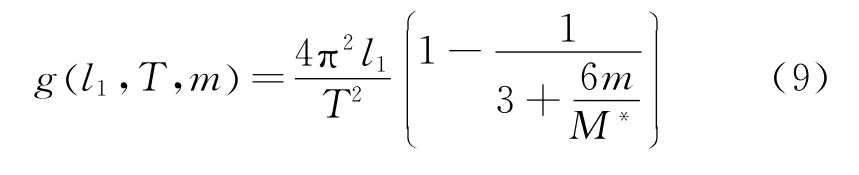
利用误差传递公式，重力加速度g的绝对误差为

实验的绝对误差与相对误差如表2所示.

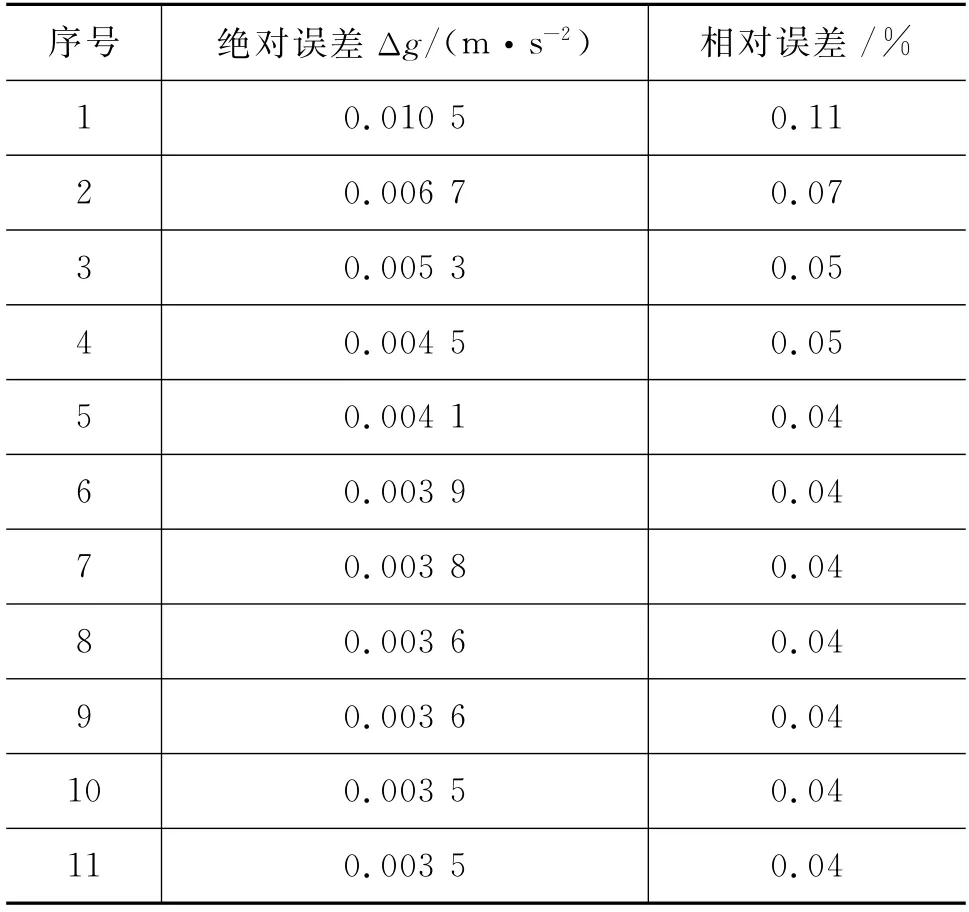
表2 实验数据误差分析

7 结论

本实验利用智能手机上的应用程序phyphox，利用手机自带的磁传感器测量复摆末端规则磁铁运动的周期，并付诸以其他计算机软件，比较廉价但准确地测量出了呼和浩特市当地的重力加速度，值为g=9.803 9 m／s2，相对准确的测量值误差仅为万分之五.这个实验还成功地测量出了钢尺顶端不规则部分的有效位形尺寸.利用复摆测量加速度有如下优势：

第一，末端悬挂物为规则的条形磁铁，磁铁的中心刚好可以和钢尺的末端重合，这就有效的减少了实验中的误差.

第二，不同于单摆实验，复摆的运动周期依赖于摆锤的质量，可以通过悬挂多块磁铁获得不同质量情况下的摆动周期，再利用回归分析的方法，减小了实验的偶然误差，从而有效地提高了实验的精度.

第三，结合智能手机上的应用程序，简化了实验流程但提高了实验精度，通过手机传感器采集数据，成本更加低廉，操作上更加简易，而且数据获取更加灵活.

此外，该实验很好地展示了刚体旋转与非刚体旋转的区别，不论是在高中阶段的教学中，还是在本科阶段力学课程的教学中，乃至在计算物理相关课程的教学中，都具有重要的启发意义.