时滞反应扩散捕食者-食饵模型的全局渐近稳定性

范宏卓，张存华

(兰州交通大学 数理学院，甘肃 兰州730070)

0 引言

捕食者-食饵模型是生物数学中的一类重要的种群模型[1-3]。假设种群在空间上的分布是均匀的，那么具有Holling-Ⅱ型功能反应函数的捕食者-食饵模型能够表示成常微分方程系统

(1)

其中，x(t)表示食饵在t时刻的种群密度，y(t)表示捕食者在t时刻的种群密度，r表示食饵种群的内禀增长率，K表示食饵的最大环境容纳量，α是捕食者对食饵的捕获率，m为半饱和常数，μ表示捕获的食饵到捕食者种群的转化率，d表示捕食者种群的死亡率。在建立模型(1)时并没有考虑捕食者种群之间的竞争关系，但大量的实验和观测数据表明捕食者之间存在竞争。因此一个更合理的捕食者-食饵模型应该建立在比率依赖理论上[4-5]，这意味着捕食者的增长率应该是一个关于食饵和捕食者数量比率的函数，满足这种功能特性的功能反应函数叫比率依赖的功能反应函数[6-7]。具有比率依赖的Michaelis-Menten型功能反应函数的捕食者-食饵模型具有形式

(2)

实际上，在种群环境中由于捕食者和食饵的迁徙行为，种群的数量在空间上的分布并不是均匀的，然而模型(2)忽视了种群空间分布的不均匀性。基于此，文献[8]提出了一类考虑种群空间分布的模型

(3)

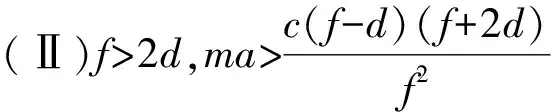
另一方面，种群的成熟需要一定时间，因此一个更加实际的模型应当考虑时滞因素的影响。基于这些原因，本文考虑以下具有时滞和比率依赖的功能反应函数的捕食者-食饵反应扩散种群模型

(4)

其中时滞τ是非负常数。本文主要研究系统(4)正常数稳态解E*=(u*,v*)的全局渐近稳定性。

1 正常数稳态解的全局稳定性

使用时滞反应扩散方程的上下解方法[9-12]分析系统(4)的正常数稳态解(u*,v*)的全局渐近稳定性。

引理1 设ma-c>0且令

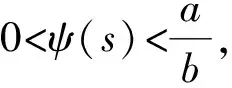
证明由于ma-c>0，于是

从而ψ(s)>0。容易得出

因为

所以

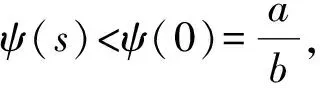
(5)

令(u(x,t),v(x,t))为系统(4)的解。则

(6)

证明由抛物型偏微分方程的极值原理,易证对任意x∈Ω和t>0，u(x,t)和v(x,t)都是非负的。又由模型(4)的第一个式子可得

(7)

由(7)式和抛物型偏微分方程的比较原理知

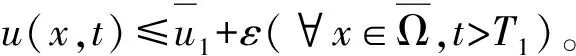
由比较原理知

再由ε的任意性得

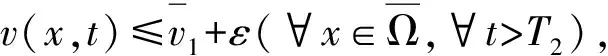
其中,

由比较原理和ε的任意性可以得到

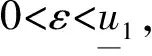
所以有

由比较原理知

再由ε的任意性得

(8)

证毕。

其中,

重复引理2和上述的推导过程并且令

其中

(9)

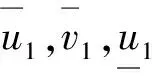
(10)

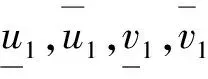
(11)

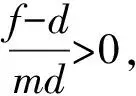
即

(12)

假设

(13)

根据ψ(s)单调递减，φ(s)单调递增和(13)式，

即

(14)

所以由数学归纳法可得(11)式成立，证毕。

(15)

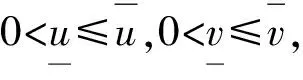
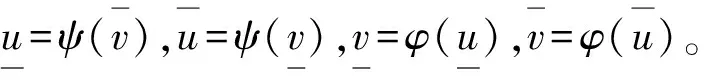
(16)

定理1 若条件(Ⅰ)或者(Ⅱ)成立，则系统(4)的正常数稳态解E*是全局稳定的。

证明由

容易得出

bψ(s)2-aψ(s)=s(ma-c-mbψ(s))。

(17)

(18)

(19)

(18)式减去(19)式得到

(20)

从而

(21)

(18)式加上(19)式得到

从而

(22)

再将(21)式代入(22)式得

将上式化简后得

(23)

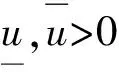
再根据(21)式可以计算得到

(24)

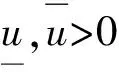
2 小结

本文在文献[8]中所提出的捕食者-食饵模型的基础上，研究了一类具有时滞的反应扩散捕食者-食饵模型，证明了该模型正常数稳态解的全局稳定性。由于本文考虑了种群成熟要消耗时间的时滞，因此本文所研究的模型比文献[8]中的模型更具有一般性。并且本文所证明的定理还表明了特定时滞不会破坏模型正常数稳态解的全局稳定性。