立体几何初步常见典型考题赏析

■张文伟

立体几何是研究现实世界中物体的形状、大小与位置关系的数学分支,在解决实际问题中有着广泛的应用。立体几何中的概念、公理、定理是同学们需要掌握的核心知识。下面就空间几何体的结构特征、立体图形的直观图、简单几何体的表面积与体积、空间点线面的位置关系以及直线、平面的平行和垂直关系,进行举例分析,帮助同学们更好地学好这部分知识。

题型1：空间几何体的结构特征与直观图

例1 (多选题)下列命题中正确的是( )。

A.棱柱的侧棱都相等,侧面都是全等的平行四边形

B.在四棱柱中,若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱

C.存在每个面都是直角三角形的四面体

D.棱台的上、下底面可以不相似,但侧棱长一定相等

解：根据棱柱的定义可知,棱柱的各个侧面都是平行四边形,但不一定全等,A 不正确。在直四棱柱中,两个过相对侧棱的截面的交线平行于侧棱,又垂直于底面,B 正确。正方体ABCD-A1B1C1D1(图略)中的三棱锥C1-ABC,其四个面都是直角三角形,C 正确。棱台的上、下底面相似且是对应边平行的多边形,各侧棱的延长线交于一点,但侧棱长不一定相等,D 不正确。应选B,C。

跟踪训练1：如图1所示,在平面直角坐标系xOy中,水平放置的正方形ABCO,点B的坐标为(4,4),则由斜二测画法画出的该正方形的直观图中,顶点B＇到x＇轴的距离为____。

图1

提示：由斜二测画法画出的直观图,如图2所示。

图2

作B＇E⊥x＇轴于点E。在Rt△B＇EC＇中,B＇C＇=2,∠B＇C＇E=45°,所以B＇E=

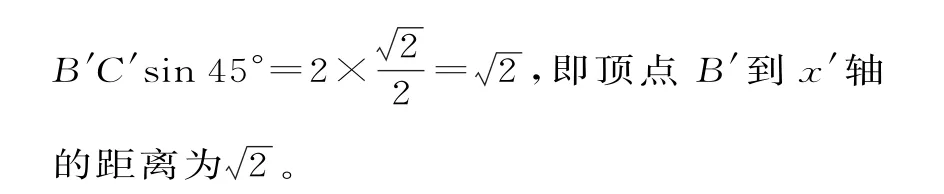
题型2：空间几何体的表面积问题

求多面体的表面积:只需将它们沿着棱“剪开”展成平面图形,利用求平面图形面积的方法求多面体的表面积。求旋转体的表面积:可以从旋转体的形成过程及其几何特征入手,将其展开后求表面积,但要搞清它们的底面半径、母线长与对应侧面展开图中的边长关系。求不规则几何体的表面积:通常将所给几何体分割成基本的柱体、锥体、台体,先求出这些基本的柱体、锥体、台体的表面积,再通过求和或作差,求出所给几何体的表面积。

图3

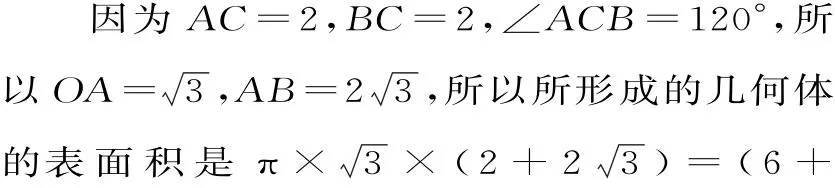
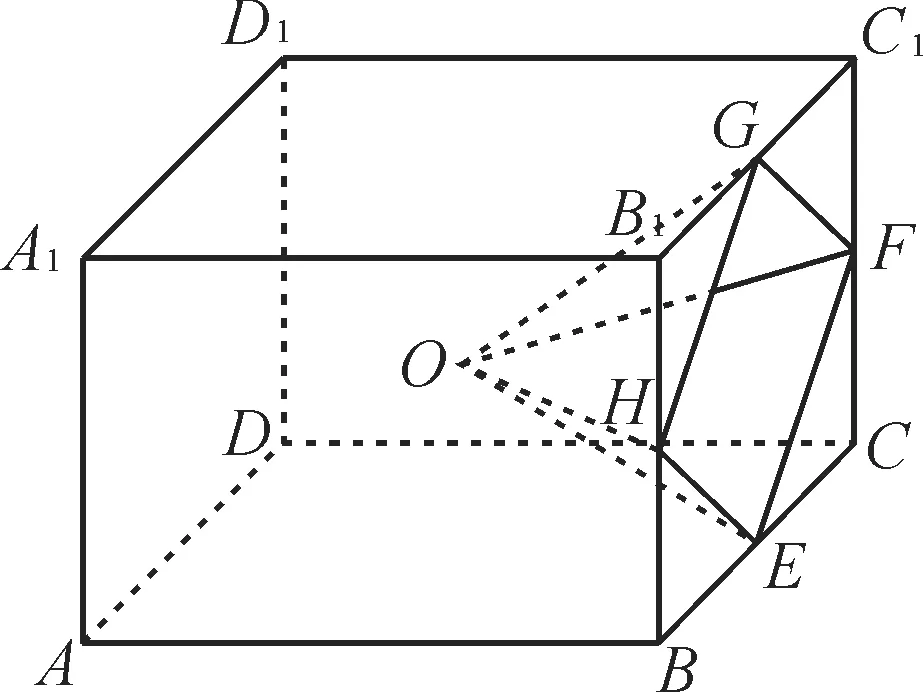
图4

跟踪训练3：如图5 所示,长方体ABCD-A1B1C1D1的体积为36,E为棱CC1上的点,且CE=2EC1,则三棱锥E-BCD的体积是( )。

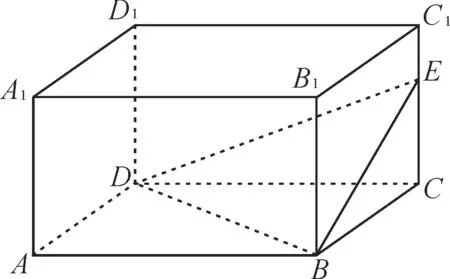
图5

题型4：与球有关的切、接问题

一个多面体的各面都与一个球的球面相切,则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。内切球的球心到多面体各面的距离均相等,外接球的球心到多面体各顶点的距离均相等。

例4 在三棱锥P-ABC中,PA=PB=PC=2,AB=AC=1,BC= 3,则该三棱锥的外接球的表面积为( )。

解：如图6,已知PA=PB=PC=2,过P作PG⊥平面ABC,垂足为G,则G为三角形ABC的外心。

图6

题型5：空间点线面之间的位置关系

判断两条直线异面的常用方法(反证法):假设两条直线不是异面直线,即两条直线平行或相交,由假设出发,经过严格的推理,导出矛盾,从而否定假设,肯定两条直线异面。直线与平面位置关系的判断:借助模型(如正方体、长方体)是解决这类问题的有效方法,证明直线在平面内,只要证明直线上两点在平面内;证明直线与平面相交,只需说明直线与平面只有一个公共点;要证明直线与平面平行,必须说明直线与平面没有公共点。判断平面与平面相交,只要找到一个交点即可;判断平面与平面平行,只要说明两个平面没有公共点。

例 5 如图 7 所示,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点。

图7

现有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线。

其中正确的结论为_____。(把你认为正确的结论序号都填上)。

解：因为点A在平面CDD1C1外,点M在平面CDD1C1内,直线CC1在平面CDD1C1内,CC1不过点M,所以AM与CC1是异面直线,①错误。取DD1的中点E,则BN//AE,但AE与AM相交,②错误。因为点B1与BN都在平面BCC1B1内,M在平面BCC1B1外,BN不过点B1,所以BN与MB1是异面直线,③正确。同理知④正确。答案为③④。

跟踪训练5：现有以下四个命题,其中正确的命题是( )。

①在平面α内有两条直线和平面β平行,那么这两个平面平行;②在平面α内有无数条直线和平面β平行,那么这两个平面平行;③平面α内的△ABC的三个顶点在平面β的同一侧且到平面β的距离相等且不为0,那么这两个平面平行;④平面α内有无数个点到平面β的距离相等且不为0,那么这两个平面平行或相交。

A.③④ B.②③④

C.②④ D.①④

提示：当两个平面相交时,一个平面内有无数条直线平行于它们的交线,即平行另一个平面,①②错误。应选A。

题型6：直线与平面的平行问题

证明直线与平面平行的关键是寻找线线平行,证明中常构造三角形中位线或平行四边形。证明直线与平面平行的五种常用方法:(1)利用线面平行的定义(无公共点)。(2)利用线面平行的判定定理(a⊄α,b⊂α,a//b⇒a//α)。(3)利用面面平行的性质定理(α//β,a⊂α⇒a//β)。(4)利用面面平行的性质(α//β,a⊄β,a//α⇒a//β)。(5)向量法,证明直线的方向向量与平面的法向量垂直。

例6 在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD为梯形,AB//CD,∠BAD=60°,PD=AD=AB=2,CD=4,E

为PC的中点。

(1)证明:BE//平面PAD。

(2)求三棱锥E-PBD的体积。

解：(1)如图8,取PD的中点F。

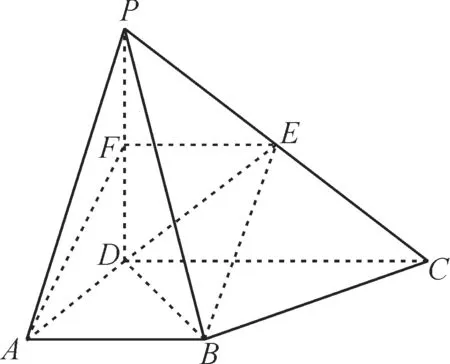
图8

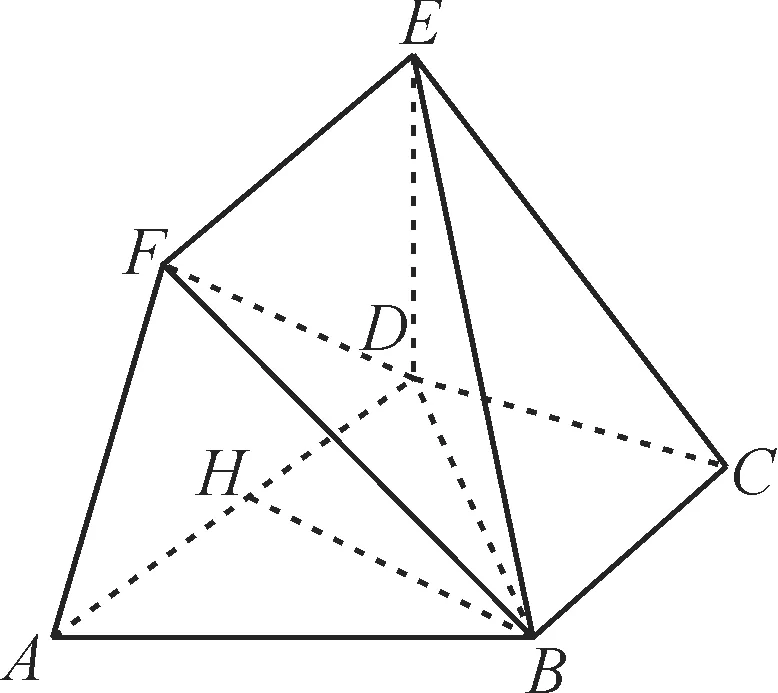
图9

(1)求证:BC//EF。

(2)求三棱锥B-DEF的体积。

提示：(1)由AD//BC,AD⊂平面ADEF,BC⊄平面ADEF,可得BC//平面ADEF。因为BC⊂平面BCEF,平面BCEF∩平面ADEF=EF,所以BC//EF。

题型7：平面与平面的平行问题

证明两个平面平行的六种常用方法:(1)利用面面平行的定义。(2)利用面面平行的判定定理。(3)垂直于同一条直线的两个平面平行。(4)如果两个平面同时平行于第三个平面,那么这两个平面平行。(5)利用“线线平行”“线面平行”“面面平行”的相互转化。(6)向量法,证明两平面的法向量平行。

例7 如图 10 所示,在三棱柱ABC-A1B1C1中,E,F,G,H分别是AB,AC,A1B1,A1C1的中点。

图10

求证:(1)B,C,H,G四点共面。

(2)平面EFA1//平面BCHG。

证明：(1)因为G,H分别是A1B1,A1C1的中点,所以GH//B1C1。又B1C1//BC,所以GH//BC,所以B,C,H,G四点共面。

(2)在△ABC中,E,F分别为AB,AC的中点,所以EF//BC。因为EF⊄平面BCHG,BC⊂平面BCHG,所以EF//平面BCHG。因为G,E分别为A1B1,AB的中点,所以A1GEB,所以四边形A1EBG是平行四边形,所以A1E//GB。因为A1E⊄平面BCHG,GB⊂平面BCHG,所以A1E//平面BCHG。又A1E∩EF=E,所以平面EFA1//平面BCHG。

跟踪训练7：如图11,在四棱锥P-ABCD中,∠ABC= ∠ACD= 90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,PA=2,AB=1。设M,N分别为PD,AD的中点。

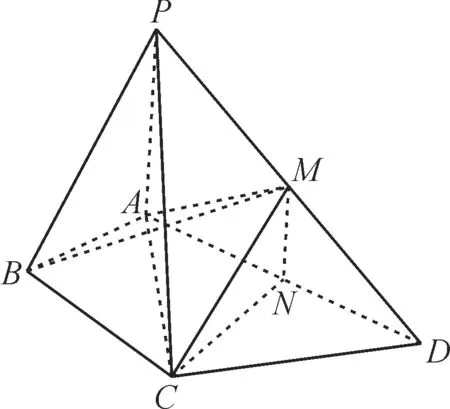
图11

(1)求证:平面CMN//平面PAB。

(2)求三棱锥P-ABM的体积。

提示：(1)由M,N分别为PD,AD的中点,可得MN//PA。

因为MN⊄平面PAB,PA⊂平面PAB,所以MN//平面PAB。

在Rt△ACD中,由∠CAD=60°,CN=AN,可得∠ACN=60°。由∠BAC=60°,可得CN//AB。由CN⊄平面PAB,AB⊂平面PAB,可得CN//平面PAB。因为CN∩MN=N,CN、MN⊂平面CMN,所以平面CMN//平面PAB。

(2)由(1)知,平面CMN//平面PAB,所以点M到平面PAB的距离等于点C到平面PAB的距离。

题型8：直线与平面的垂直问题

证明直线与平面垂直的四种常用方法:(1)利用线面垂直的判定定理。(2)利用两平行线中的一条与平面垂直,则另一条也与这个平面垂直。(3)利用一条直线垂直于两个平行平面中的一个平面,则与另一个平面也垂直。(4)利用面面垂直的性质定理。

例8 如图12,PA⊥圆O所在的平面,AB是圆O的直径,C是圆O上的一点,E,F分别是点A在PB,PC上的射影。

图12

给出下列四个结论:①AF⊥PB;②EF⊥PB;③AF⊥BC;④AE⊥平面PBC。其中正确结论的序号是____。

解：由PA⊥平面ABC,BC⊂平面ABC,可得PA⊥BC。因为AB是圆O的直径,C是圆O上一点,所以BC⊥AC。因为PA∩AC=A,所以BC⊥平面PAC。又AF⊂平面PAC,所以BC⊥AF,③正确。因为AF⊥PC,PC∩BC=C,所以AF⊥平面PBC。又PB⊂平面PBC,所以AF⊥PB,①正确。因为AE⊥PB,AF⊥PB,AE∩AF=A,所以PB⊥平面AEF。又EF⊂平面AEF,所以PB⊥EF,②正确。因为AF⊥平面PBC,AF∩AE=A,所以AE不与平面PBC垂直,④错误。答案为①②③

跟踪训练8：如图13,S是Rt△ABC所在平面外一点,且SA=SB=SC,D为斜边AC的中点。

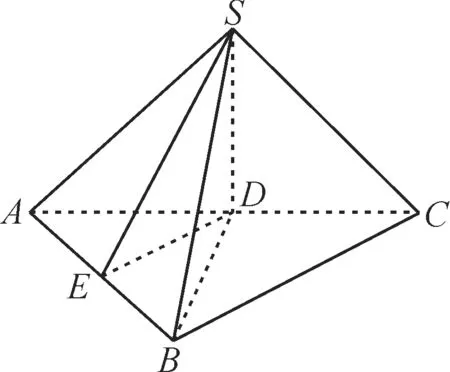
图13

(1)求证:SD⊥平面ABC。

(2)若AB=BC,求证:BD⊥平面SAC。

提示：(1)取AB的中点E。 在Rt△ABC中,由D,E分别为AC,AB的中点,可得DE//BC,所以DE⊥AB。

由SA=SB,可得SE⊥AB。因为SE∩DE=E,所以AB⊥平面SDE。又因为SD⊂平面SDE,所以AB⊥SD。

在△SAC中,由SA=SC,D为AC的中点,可得SD⊥AC。又AC∩AB=A,所以SD⊥平面ABC。

(2)由AB=BC,可得BD⊥AC。由(1)知SD⊥平面ABC。因为BD⊂平面ABC,所以SD⊥BD。又SD∩AC=D,所以BD⊥平面SAC。

题型9：平面与平面的垂直问题

证明两个平面垂直,关键是寻找其中一个平面内的一条直线与另一个平面垂直,也就是利用线面垂直,得到面面垂直。已知两个平面垂直,一般要在一个平面内作交线的垂线,转化为线面垂直,然后进一步转化为线线垂直。求作空间一点向平面引垂线(段)或求几何体的高,可利用面面垂直的性质。

例9 如图14,点N为正方形ABCD的中心,△ECD为正三角形,平面ECD⊥平面ABCD,M是线段ED的中点,则( )。

图14

A.BM=EN,

且直线BM,EN是相交直线

B.BM≠EN,且直线BM,EN是相交直线

C.BM=EN,且直线BM,EN是异面直线

D.BM≠EN,且直线BM,EN是异面直线

解：取CD的中点F,DF的中点G(作法略)。由△ECD是正三角形,可得EF⊥CD。由平面ECD⊥平面ABCD,可得EF⊥平面ABCD,所以EF⊥FN。

提示：如图15,过点P作PO⊥平面ABC于O,则PO为P到平面ABC的距离。

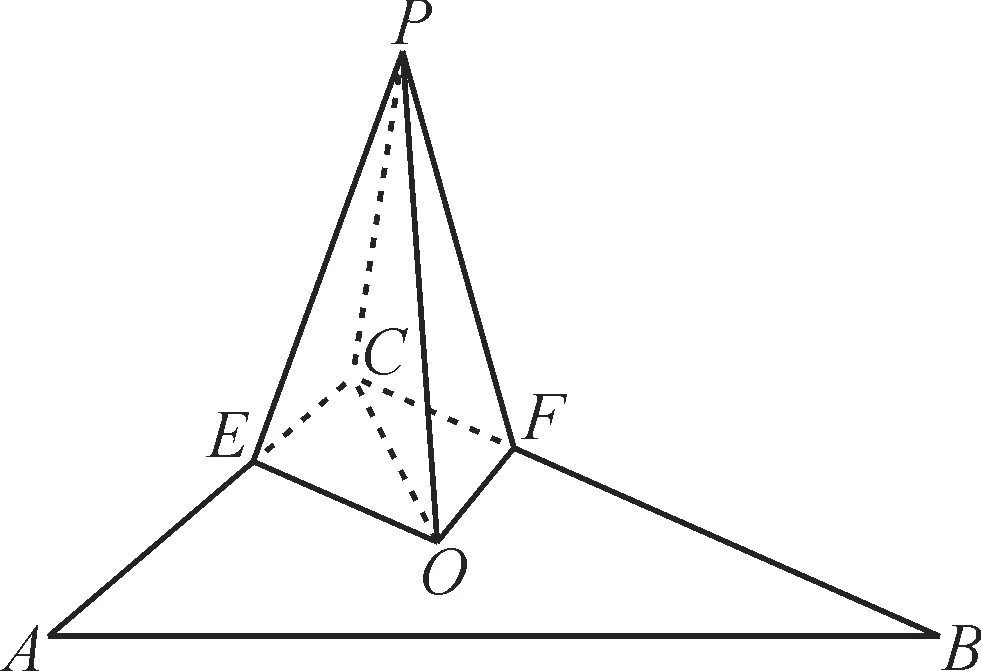
图15

过O作OE⊥AC于E,OF⊥BC于F,则PE⊥AC,PF⊥BC。

题型10：立体几何中的探索性问题

探索性问题一般可以分为判断存在型、条件探索型、结论探索型、类比推理型、知识重组型等。立体几何中的探索性问题一般以判断存在型为主。这类问题一般的设问方式是“是否存在…,若存在…,若不存在…”。由于没有一个明确的结论,在没有经过深入分析、严格计算和推理论证前其存在性是未知的。

例10 如图16 所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足____时,平面MBD⊥ 平面PCD。(只要填写一个你认为是正确的条件即可)

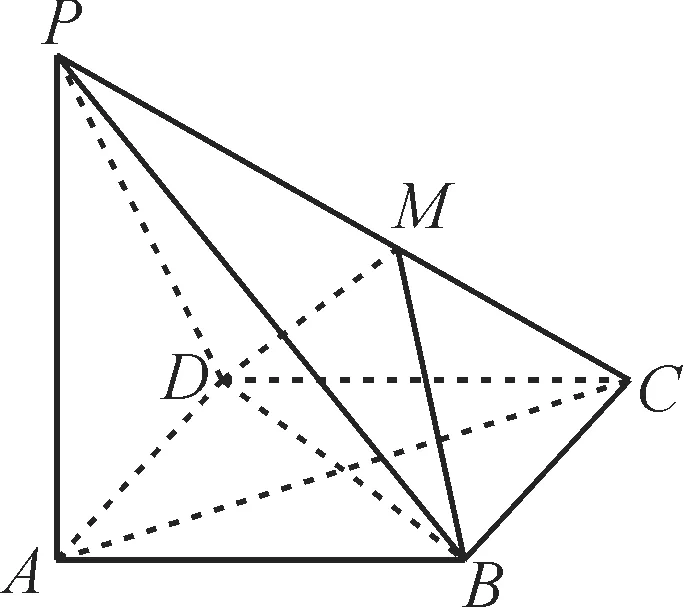
图16

解：由四边形ABCD的各边都相等,可得AC⊥BD。由PA⊥底面ABCD,可得PA⊥BD。因为PA∩AC=A,所以BD⊥平面PAC,所以BD⊥PC。

当DM⊥PC(或BM⊥PC)时,则PC⊥平面MBD。而PC⊂平面PCD,所以平面MBD⊥平面PCD。

答案为DM⊥PC(或BM⊥PC)。

跟踪训练10：如图17

图17

所示,一张A4纸的长、宽分别为2 2a、2a,A,B,C,D分别是其四条边的中点。现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体。下列关于该多面体的命题,正确的是____。(写出所有正确命题的序号)

①该多面体是三棱锥;②平面BAD⊥平面BCD;③平面BAC⊥平面ACD;④该多面体外接球的表面积为5πa2。