基于卷积神经网络的时频域CT重建算法

李昆鹏，张鹏程*，上官宏，王燕玲，杨 婕，桂志国

（1.中北大学信息与通信工程学院，太原 030051；2.生物医学成像与影像大数据山西省重点实验室（中北大学），太原 030051；3.太原科技大学电子信息工程学院，太原 030024；4.山西财经大学信息学院，太原 030006；5.山西中医药大学健康服务与管理学院，太原 030024）

0 引言

X 射线计算机断层扫描（Computed Tomography，CT）是一种在临床和工业中被广泛使用的成像技术。在断层成像中所需解决的主要问题是如何通过投影数据恢复出图像数据。随着断层成像技术在许多领域中的广泛使用，众多研究人员致力于研究CT 重建方法。目前主要的CT 重建方法可分为三类：解析重建算法、迭代重建算法和基于神经网络的重建方法。

依据傅里叶中心切片定理，解析重建算法建立了待重建物体的Radon 变换与其二维傅里叶变换之间联系。滤波反投影（Filtered Back-Projection，FBP）算法是经典的解析重建算法，广泛应用于CT 重建中。FBP 算法的优点是计算速度快，计算存储消耗小；然而，当投影数据角度较少或投影数据中包含大量噪声时，该算法重建所得图像质量将大幅降低。

区别于解析重建算法仅对投影数据处理，CT 重建迭代算法同时考虑投影数据和重建图像的统计特性。迭代重建算法通过给目标函数添加不同的正则项，从而包含了不同的统计模型，如全变分（Total Variation，TV）、广义全变分、非局部信息和字典学习等。在目标函数中使用正则项，显著地提升了重建后图像的视觉效果。然而，为了获得较好的重建结果，需要谨慎设置迭代算法中的超参数以及严格控制迭代次数。在迭代重建算法求解过程中，导致计算代价高的主要原因是反复进行的投影/反投影运算。尽管能通过并行计算方法对该部分进行加速，但是仍旧比解析重建算法消耗更多计算时间和储存空间。

近年来，深度学习在计算机视觉和自然语言处理领域得到了广泛的应用。卷积神经网络（Convolutional Neural Network，CNN）是目前应用最广泛的深度学习算法之一。由于很难采用CNN 表征投影域到图像域之间的复杂映射关系，因而文献［16-17］在网络中使用全连接技术建立CT 重建网络。在重建网络中采用全连接技术导致网络规模过大，增加了网络训练和实际应用的难度。

为了避免在CT 重建网络中使用全连接技术，研究人员将迭代重建算法的迭代过程展开成固定的

N

步迭代，用CNN替换其中每一次迭代。一方面，迭代重建算法的正则项可以直接用CNN 进行替换；另一方面，通过交替方向乘子法将目标函数分解为几个子目标函数，这些子目标函数优化结果等价于原目标函数的优化结果。部分子目标函数可以通过CNN 实现，从而避免了在重建网络中使用全连接技术，减少了重建网络的参数量。但是相较于解析重建算法，这类方法所需计算量仍然非常大。

与上述两类基于神经网络的重建方法不同，双域重建算法采用反投影算子来实现投影域数据到图像域数据的转换，在投影域与图像域分别利用CNN 进行滤波和图像恢复。该类方法避免了在重建网络中使用全连接技术，且相较于迭代展开重建算法，减少了重建所需计算量，因而被越来越多的研究人员采用。

与传统FBP 算法相比，使用特殊的滤波器替换原有理想斜坡滤波器对投影数据进行滤波，可以得到与迭代重建算法重建视觉效果相近的结果。该滤波器可以通过对迭代重建算法进行理论推导直接得出，也可以通过迭代重建算法进行优化求解得出。根据傅里叶中心切片定理可知，未经过滤波而直接进行反投影将引起重建图像的低频分量过度加权，导致图像变得模糊。传统FBP 算法的滤波器为理想斜坡滤波器，该滤波器是一个高通滤波器，在实际应用中很难实现。对此，常采用加窗的方法对理想斜坡滤波器进行修正。通常使用理想矩形窗对理想斜坡滤波器进行加窗得到Ram-Lak 滤波器。虽然采用Ram-Lak 滤波器重建的图像可以有效地去除重建图像低频模糊效应，但是重建图像会存在明显的Gibbs 震荡现象。针对Ram-Lak 滤波器所引起的重建图像震荡效应，文献［2］提出选取sinc 函数作为窗函数得到Shepp-Logan 滤波函数，该方法弥补了Ram-Lak 滤波器的不足；但是Shepp-Logan 滤波器在低频段偏离理想滤波器，导致重建图像的低频部分视觉效果差。解析重建算法还易受投影数据质量的影响，当投影数据角度较少或投影数据中包含大量噪声时，重建所得图像视觉效果明显变差。理论上说，采用特殊的滤波器对投影数据进行滤波，可以进一步改善传统FBP 算法重建图像中低频偏离、高频震荡等现象。

针对采用时域滤波器进行解析重建导致重建后图像存在伪影和图像细节丢失等问题，本文利用卷积神经网络强大的特征提取和表达能力，设计了一个结合频域处理的双域CT 重建神经网络（Dual Domain Frequency Network，DDFre-Net）。本文主要工作有以下几点：1）为了解决时域滤波器进行解析重建导致重建后图像存在伪影和图像细节丢失的问题，在频域使用CNN 对投影数据进行处理，构建了投影域网络Fre-CNN；2）为了解决在投影域到图像域转过程中使用全连接技术而导致网络参数量大的问题，实现了正投影/反投影线性算子，构建了反投影层；3）为了提高重建网络在训练过程中的收敛速度，获得较高质量的重建图像，构建了图像域网络Img-CNN；4）为了抵消神经网络对结果图像的模糊效应，保留重建图像细节，在原最小均方误差损失函数基础上引入多尺度结构相似度损失函数来组成复合损失函数以保留更多重建图像的细节。为了验证本文算法的有效性，将本文算法与FBP 算法、TV 算法、残差编解码卷积神经网络（Residual Encoder-Decoder CNN，RED-CNN）算法在临床数据集上作对比。实验结果表明，本文算法重建的图像伪影少，信噪比高，且速度快。

1 DDFre-Net

本文构建了一个基于双域的CT 重建网络DDFre-Net，该网络结合了投影数据频域处理和图像数据时域处理，总体架构如图1（a）所示。DDFre-Net 主要由三部分组成：投影数据频域处理网络Fre-CNN、反投影层（Back-Projection）和图像数据时域处理网络Img-CNN。在DDFre-Net 中，输入的投影数据首先在Fre-CNN 中进行处理。在Fre-CNN 中，投影数据先经Spa2Fre 层进行傅里叶变换，然后经过频域编解码的CNN处理，最后在Fre2Spa 层进行傅里叶反变换。反投影层（Back-Projection）实现了投影域到图像域的变换功能，该层网络的参数是固定的。在DDFre-Net 的图像域处理中，Img-CNN 对反投影层输出的图像进行进一步恢复，最终得到重建图像。DDFre-Net 是一个端到端的卷积神经网络，在网络的输出端采用统一的损失函数对网络进行约束。

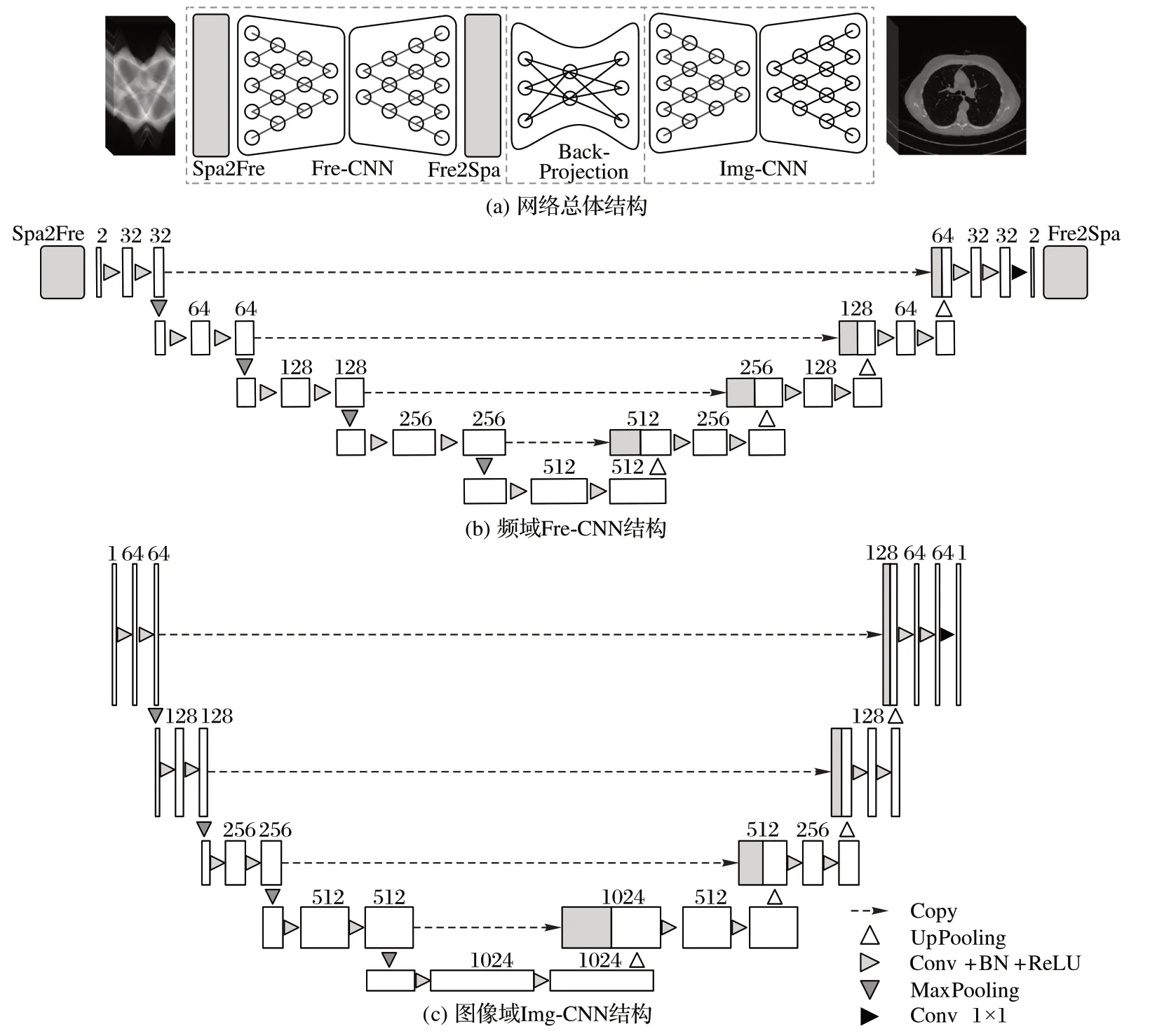
图1 DDFre-Net结构Fig.1 DDFre-Net structure

1.1 投影域网络

在传统FBP 算法中，通常采用理想斜坡滤波器对投影数据进行滤波处理从而改善重建图像后图像的质量。对投影数据的滤波处理可以在时域进行，也可以在频域进行。时域滤波是通过将投影数据与时域滤波器进行离散卷积实现；频域滤波则是先各自将投影数据和滤波器进行傅里叶变换，在频域将二者直接相乘实现。

传统FBP 算法中的理想滤波器是根据傅里叶中心切片定理推导得到。由于该理想滤波器是个频带无限的滤波函数，很难直接在实际中应用。因而，为了精确地表征该斜坡滤波器，Ghani 等利用CNN 替换理想斜坡滤波器，对投影数据进行滤波处理；Whiteley 等针对由于探测器损坏或灵敏度不足而导致的投影数据缺失的问题，利用CNN 在时域对正电子发射型计算机断层显像（Positron Emission computed Tomography，PET）投影数据进行恢复和滤波处理。Wang 等在频域中利用CNN 对PET 投影数据进行滤波。相较于CNN 在时域中的滤波处理，频域处理的重建网络模型具有更强的泛化能力。因此，本文在频域中构建网络对投影数据进行滤波处理。

频域处理网络的详细结构如图1（b）所示，最左端是Spa2Fre 层，中间是频域编解码网络Fre-CNN，最右端是Fre2Spa 层。在Spa2Fre 层中对时域投影数据进行傅里叶变换；在Fre2Spa 层中对频域滤波后的投影数据进行傅里叶反变换；由于基于编解码结构的CNN 具有较强的特征提取和信息表征能力，所以本文采用基于U-Net 的CNN来构建频域滤波网络。如图1（b）所示，频域滤波编解码网络Fre-CNN深度为4，每一级由编码子网络与解码子网络组成。为避免深度网络训练过程中梯度消失问题，同级网络之间通过跨层连接，将同级编码端低维特征补充到解码端高维特征。每一级的编码子网络和解码子网络都由相同的网络结构组成，该网络结构包含两个连续的卷积层（Convolutional layer，Conv），在每次卷积操作后均有一个批规范化（Batch Normalization，BN）操作和一个线性修正单元（Rectified Linear Unit，ReLU）作为激活函数进行激活。其中，卷积操作的卷积核大小为1×3。在编码端，两次连续卷积后进行一次1×2 的池化操作，其步长为1×2；在解码端，两次连续卷积之后进行一次1×2 的上采样（Up-Conv）操作，其步长为1×2。投影域网络卷积特征图数量和数据大小如图1（b）所示。投影域网络计算式如下：

其中：

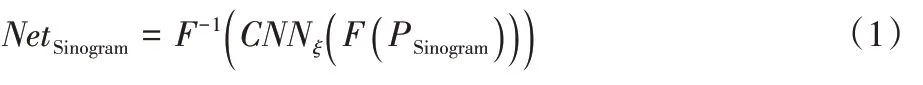
P

为投影数据；

F

和

F

分别表示傅里叶正变换和傅里叶反变换；

Net

表示该网络的输出；

CNN

为投影数据在频域中的滤波网络。

1.2 反投影层

在二维扇形束CT 重建过程中，在

N

个投影角度下获取投影数据，每个角度下的投影数据长度为

N

，所有投影数据表示为

p

。重建后的图像为

x

，其大小为

N

×

N

。于是，CT 重建问题可以表述为求解以下线性方程：

其中：

A

是系统矩阵，其大小为

NN

×

NN

。CT 重建过程便是根据系统矩阵

A

从投影数据

p

中恢复出未知图像

x

。系统矩阵

A

中的元素

a

表示第

i

条X 射线穿过模体在第

j

号像素内产生的贡献。系统矩阵

A

与图像

x

的乘积被称为正投影，而系统矩阵的转置

A

与投影数据

p

的乘积被称为反投影。在实际应用中，由于系统矩阵非常庞大，通常采用即时计算的方式计算正投影系统矩阵

A

和反投影系统矩阵

A

。CT 图像重建过程可以表示为滤波后投影数据

P

与反投影矩阵

A

直接相乘的反投影过程。理论上说，该反投影过程可以使用全连接技术实现。由于实际CT 重建问题中投影数据和重建图像的尺寸较大，导致全连接层的网络参数非常庞大，阻碍了该技术在常规电脑上的实现。为了解决该问题，本文构造了一个权重参数固定的反投影层，采取即时计算的方式计算反投影矩阵

A

和正投影矩阵

A

。反投影层的前向操作可以表示为：

其中：反投影层的输入

x

来自于投影域网络的输出，

x

表示该反投影层的输出。网络在训练过程中，误差反向传播通过反投影层可以表示为：

其中：

e

表示来自于图像域网络的反馈误差，该反馈误差经过正投影操作得到误差

e

，反馈至投影域网络。为了提升DDFre-Net 重建网络的性能，正投影采用射线驱动方法进行计算，反向投影则采用像素驱动方法进行计算。反投影层可以表示为：

其中：

Net

为反投影层输出；

BP

(·)为反投影层；

Net

为投影域网络输出。

1.3 图像域网络

为了进一步改善重建图像视觉效果，在反投影层之后增加一个图像域处理网络Img-CNN。如图1（c）所示，该网络是一个U-Net 结构的网络，包含一个编码器子网络（左半部分）和一个解码器子网络（右半部分）。编码器子网络和解码器的深度设为4。在编码端，每一级包含两个连续的卷积块和池化块。每个卷积块包含两个卷积层，每个卷积层采用步长为1 的3×3 卷积核进行卷积，同时每个卷积层紧跟一个批规范化层及一个ReLU 非线性激活函数层。在连续两个卷积块后，有卷积核大小为3×3、步长为2×2 的最大池化层进行下采样操作。池化层输出的特征图数量是输入特征图两倍。在解码端，输入的特征图先经过Up-Conv 操作，通过插值操作使特征图大小增大为原来的两倍。在Up-Conv 操作中，输出特征图数量为输入特征图数量的1/2，同时，Up-Conv 输出的特征图与对应同一编码端卷积输出特征图进行级联操作。每一级编码端和解码端采用跨层连接操作，解决深度神经网络梯度消失的问题，并提高网络训练的收敛速度。在Img-CNN最后，采用一个卷积核大小为1×1、步长为1 的卷积层进行网络特征融合，输出重建图像。Img-CNN 每层卷积数量和每层图像大小如图1（c）所示。图像域网络可用下列计算式表示：

其中：

Net

为网络输出；

CNN

为图像域数据处理网络；

Net

为反投影层的输出。

1.4 网络损失函数

本文采用像素级损失函数和结构相似性损失函数共同对重建网络进行约束。本文所使用的像素级损失函数为最小均方误差（Mean Square Error，MSE），如式（7）所示：

其中：

x

是重建图像，

x

则是参考图像。

但MSE 损失通常会导致网络收敛于训练数据的均值，导致重建后图像存在平滑模糊、缺少细节和纹理特征的现象。故本文采用MSE 损失函数和多尺度结构相似度（Multi Scale Structural Similarity，MS-SSIM）损失函数（如式（9）所示）共同作为重建网络损失函数，进一步地保持重建图像细节。MSE 损失和MS-SSIM 损失函数公式如下：

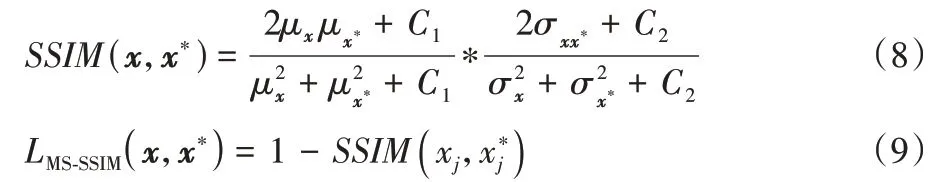
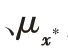
2 实验设置

2.1 数据集

本文采用“2016 NIH-AAPM-Mayo Clinic 低剂量挑战赛”所提供的公开数据集，该数据集包含了20 例不同病人的胸部正常计量的CT 数据，共3 570 张CT 重建图像。由于该临床数据集采用螺旋轨迹扫描方式获取，因而原始投影数据不能直接被用于扇形束CT 重建。在本文实验中，在一定扫描参数下通过正投影算法重新获取投影数据，分别产生了投影角度数目为90、180 和360 的投影数据。生成投影数据的探测器数量是768，采样间隔是1 mm；重建图像尺寸为512×512，采样间隔为0.585 9 mm×0.585 9 mm；射线源到探测器中心距离为1 068.0 mm；射线源到旋转中心距离为595.0 mm。19 个病例的数据用于重建网络的训练，剩余1 个病例的194 个投影数据用于重建算法的测试。

为了进一步地验证本文算法的减少重建图像伪影和抑制重建图像噪声的能力，通过在投影中加入电子噪声和泊松分布的噪声来生成带噪声的数据集，从而模拟真实的投影数据：

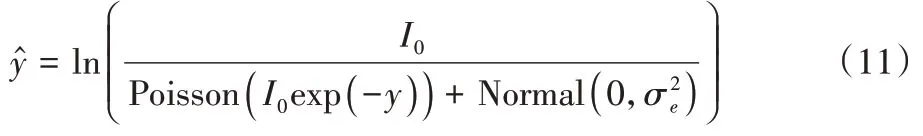
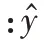
2.2 实验环境

本文算法采用深度学习Pytorch 框架进行构建，采取Adam 优化算法作为重建网络训练的优化算法，初始学习率设置为10，批量大小设置为1，每训练1 000 次保存一个模型。选取的对比算法为FBP、TV 和RED-CNN 三种。FBP 算法采用Ram-Lak 滤波器对投影数据进行滤波，并使用本文算法中的反投影层对滤波后的投影数据进行反投影操作，得到重建后的图像。TV 算法则是采用TRIGER工具箱自带的自适应步长的全变差最小（Adaptive Steepest Decent Projection Onto Convex Sets，ASD-POCS）算法进行CT 重建，其中迭代次数设置为40。在PyTorch 框架下对RED-CNN 算法进行复现，网络训练参数设置与文献［35］一致。

本文算法和对比算法均在同一台工作站上进行实验，该工作站硬件参数配置如下：CPU 型号为Intel Core i7-9700k 3.6 GHz，内存64 GB，GPU：NVIDIA RTX 3090 24 GB。该工作站的操作系统为Ubuntu20.04 LTS。

2.3 评价指标

本文分别采用峰值信噪比（Peak Signal to Noise Ratio，PSNR）、结构相似性（SSIM）和归一化均方误差（Normalized MSE，NMSE）这三个指标对重建结果进行评价。SSIM 公式为式（8），PSNR 和NMSE 的计算公式如下：

其中：

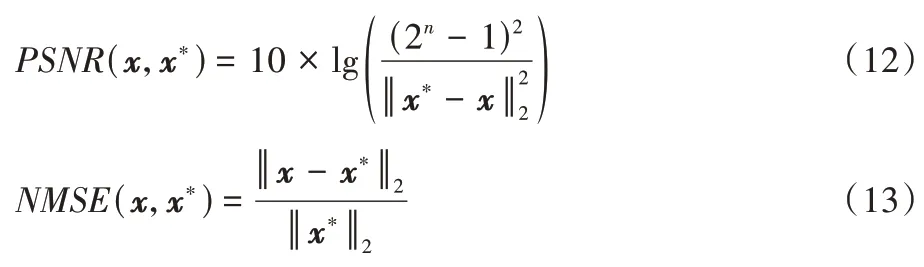
n

为图像像素的比特数，一般取8 或16；

x

是重建图像，而

x

则是参考图像；

μ

代表图像均值；PSNR 的单位是dB，数值越大表示图像失真越小；SSIM 值位于（0，1），该值越接近1表示重建图像质量越好；NMSE 衡量结果图像和参考图像之间的差异，NMSE 值越低表示重建图像质量越高。

3 不带噪声数据实验与结果分析

为了验证本文算法的有效性，分别选取了同一病例三个不同部位的投影数据作为各算法的输入，投影数目分别为360、180 和90 个。在重建结果展示中，重建部位一和重建部位二图像的视窗均为［-900，2 100］HU，重建部位三图像的视窗［-360，440］HU。在重建结果残差图像中，各图像的视窗为［-512，512］HU。最后，给出了不同算法在同一病例测试集上整体评价指标和各个算法的计算时间。

3.1 360个投影数目的重建结果分析

图2 为不同算法对同一病例的三个不同组织部位的CT重建图像结果对比。在各重建图像的正下方为该重建图像PSNR 和SSIM 的数值指标，左下角是感兴趣区域（图2（a）中白色矩形位置）的放大图像。

图2 不同算法在投影数目为360时的重建结果对比Fig.2 Comparison of reconstruction results under 360 projections by different algorithms

图3 为不同重建算法重建所得图像与参考图像的残差图像。各个残差图像的下方为计算的NMSE 指标数值。综合图2 和图3 可得，采用FBP 算法进行重建，重建结果的噪声和伪影较为明显，重建图像视觉效果欠佳；TV 算法能很好地保留图像的细节信息，在抑制噪声和保留图像的结构信息方面表现良好；RED-CNN 算法虽然计算的PSNR 指标较高且能够在一定程度上抑制噪声并消除伪影，但是所得的图像细节较为模糊；本文算法可以有效地抑制噪声、去除伪影和保留纹理等细节，在视觉效果方面优于对比算法。虽然TV 算法计算所得重建图像的评价指标略高于本文算法，但是二者在图像视觉效果方面并无太大差异。

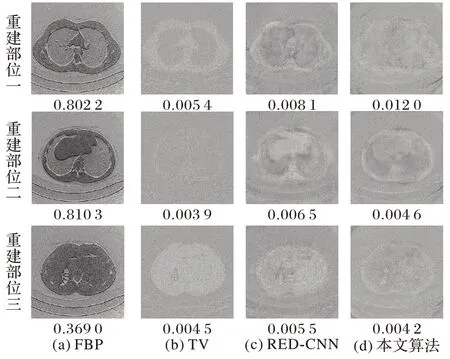
图3 不同算法在投影数目为360时的重建结果残差图Fig.3 Difference images of reconstruction result under 360 projections by different algorithms

3.2 1 80个投影数目的重建结果分析

随着投影角度数量的减少，不同重建算法计算所得重建图像的评价指标PSNR、SSIM 和视觉效果均会有所下降。图4 是本文算法和对比算法在180 个投影数目下的重建结果图，相应的重建结果残差图如图5 所示。

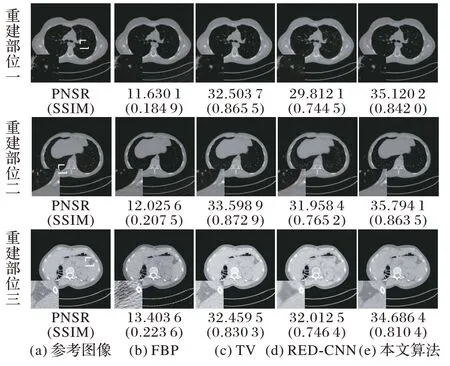
图4 不同算法在投影数目为180时的重建结果对比Fig.4 Comparison of reconstruction results under 180 projections by different algorithms

从图4 和图5 可以观察到，传统的FBP 算法明显增加了重建图像的噪声和伪影，无法很好地获得重建信息。TV 算法虽然可以有效地减少重建后图像中的噪声和伪影，但是仍然模糊了图像的细节，且重建后图像中存在一些条状伪影。RED-CNN 算法严重地平滑了重建后图像的细节。相较于TV 算法所得结果，RED-CNN 方法重建所得图像虽然PSNR数值较高，但是由于该方法严重地平滑了所得图像的细节，因此视觉效果较差。相较于对比算法，本文算法有效地保留了重建图像的结构和纹理等细节信息，且图像质量评价指标和视觉效果比对比算法高。

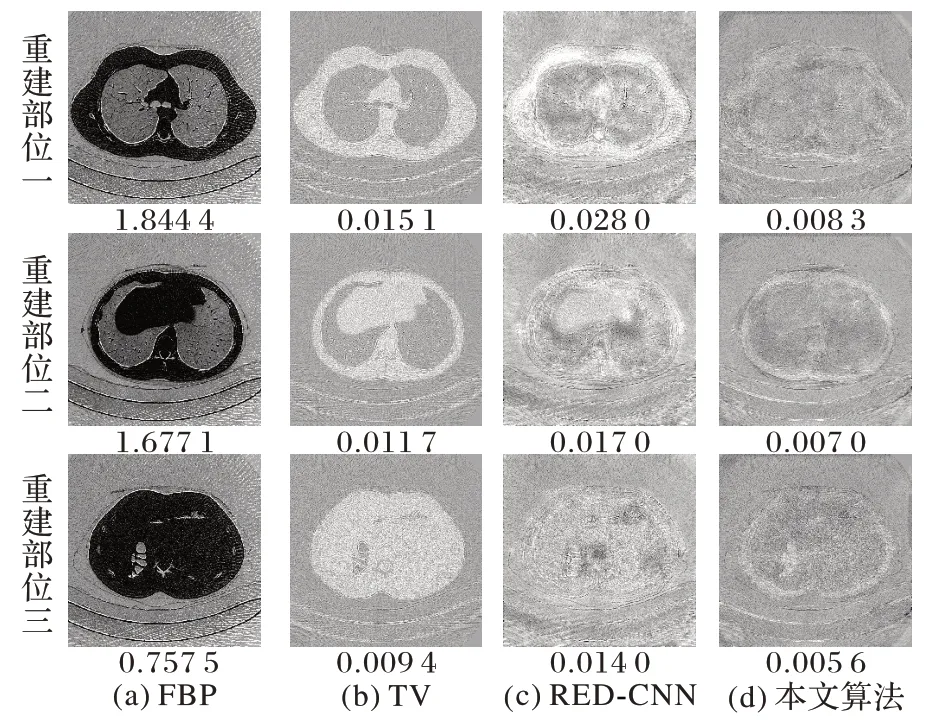
图5 不同算法在投影数目为180时的重建结果残差图Fig.5 Difference images of reconstruction result under 180 projection by different algorithms

3.3 90个投影数目的重建结果分析

随着投影数据角度数量的进一步减少，不同重建算法所得重建图像的质量均有明显的下降。图6是90个投影数目下4种算法的重建图像，相应的重建结果残差图如图7所示。

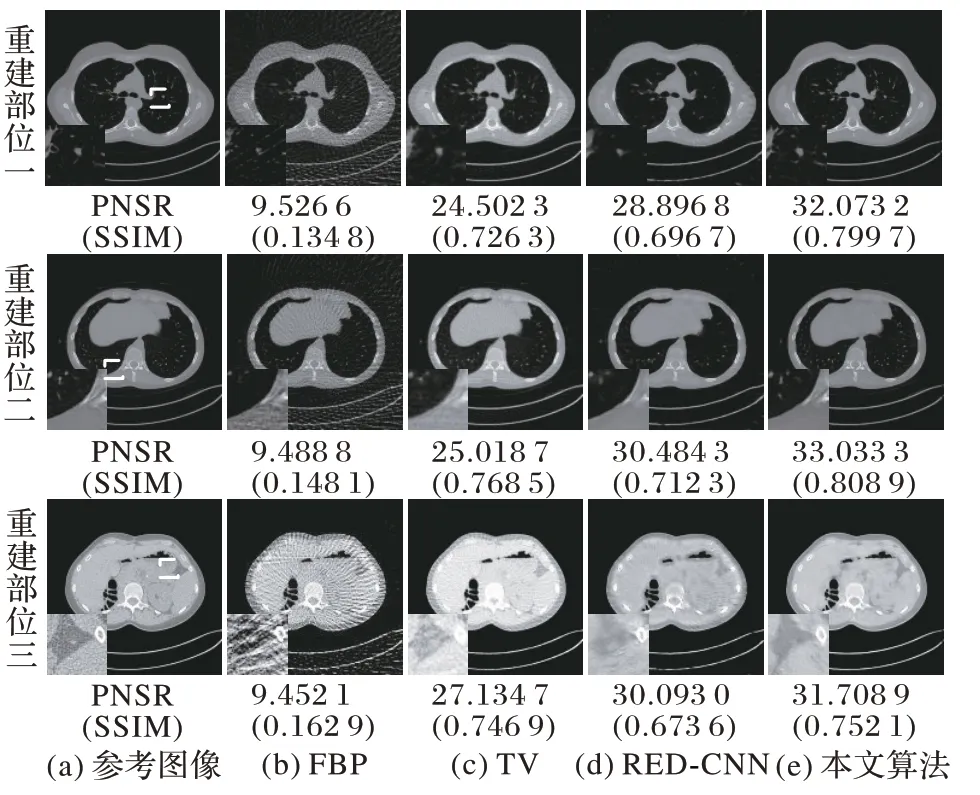
图6 不同算法在投影数目为90时的重建结果对比Fig.6 Comparison of reconstruction results under 90 projections by different algorithms

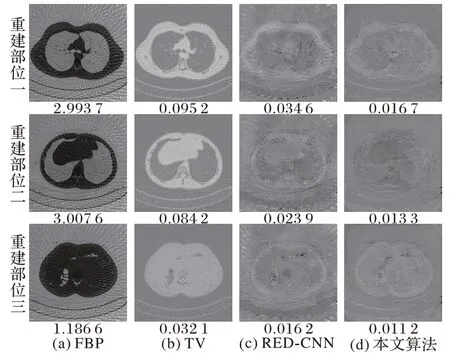
图7 不同算法在投影数目为90时的重建结果残差图Fig.7 Difference images of reconstruction result under 90 projection by different algorithms

从图6 中不难发现，三种对比算法计算所得重建图像均丢失了图像的结构特征，存在较为严重的条纹伪影和噪声。本文提出的算法虽然也会模糊图像，并导致图像丢失结构细节，但是与三种对比算法相比，本文算法可以更好地保留图像结构信息并在指标PSNR、SSIM、NMSE上获得更好数值。

3.4 重建测试集指标以及重建时间分析

表1 是对比算法和本文算法在测试集上单张图像的重建时间对比。从表1 重建时间对比中可以看出，FBP 算法计算速度最快，TV 算法计算耗时最长，本文所提DDFre-Net 算法计算时间介于RED-CNN 算法与FBP 算法之间。

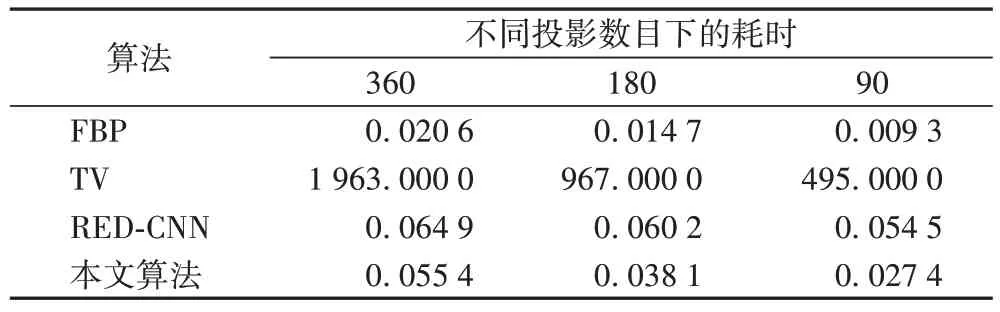
表1 不同算法单张图像重建耗时 单位：sTab 1 Reconstruction of time single image by different algorithms unit：s

表2是对比算法和本文算法在测试集上的PSNR、SSIM和NMSE 三个指标。从表2 可以看出，本文所提出DDFre-Net 算法在投影角度数目为360 时测试集上指标略低于TV 算法，但在投影角度数目为180 和90 时，在测试集上各指标均要优于FBP、TV 和RED-CNN 三种算法。综上可知，本文算法在保证重建图像质量较好的前提下，计算速度快。

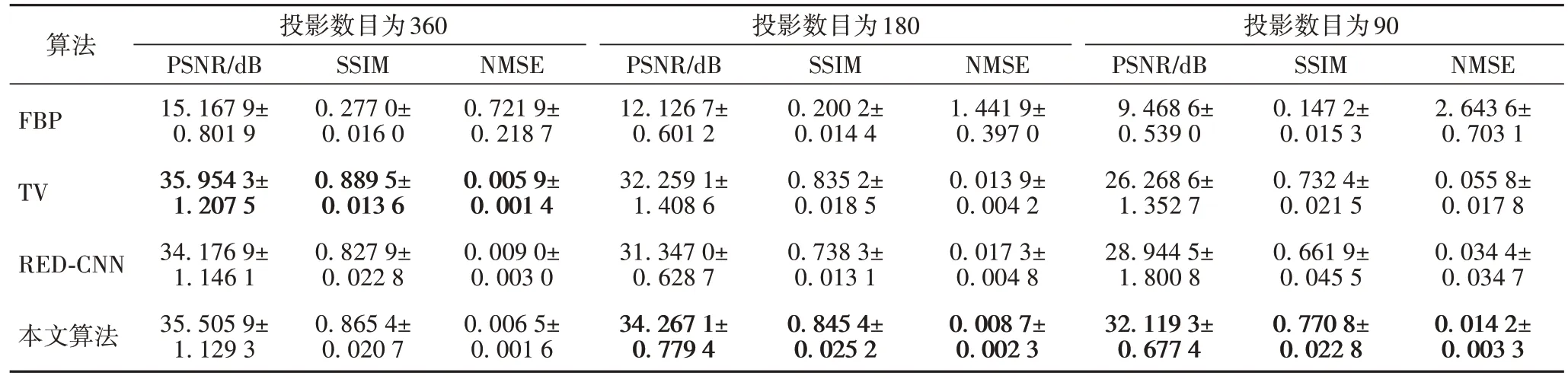
表2 不同算法测试集上指标对比Tab 2 Index comparison of different comparison algorithms under different projections

3.5 网络训练损失函数曲线

图8 是本文DDFre-Net 算法在不同投影角度数量下的网络训练损失。从图8 中可以观察到，随着网络训练次数的增加，网络的损失逐渐减小，从而说明该网络是收敛的。

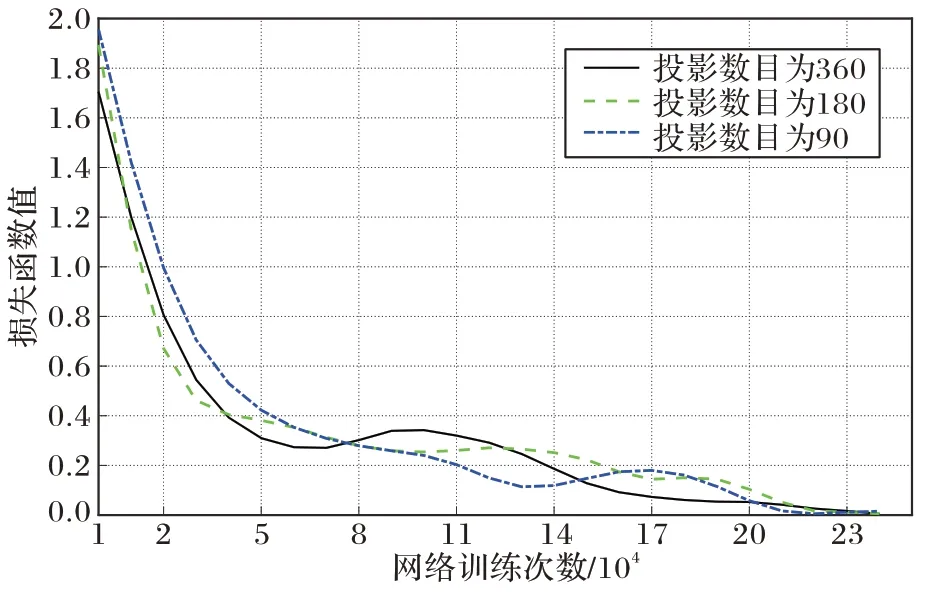
图8 DDFre-Net训练损失Fig.8 DFre-Net training loss

4 带噪声数据实验与结果分析

为了进一步验证算法的鲁棒性，在带噪声的投影数据上进行CT 重建。图9 分别 为FBP 算法、TV 算法、RED-CNN 算法和本文算法的重建结果，所得图像与参考图像的残差图如图10 所示。

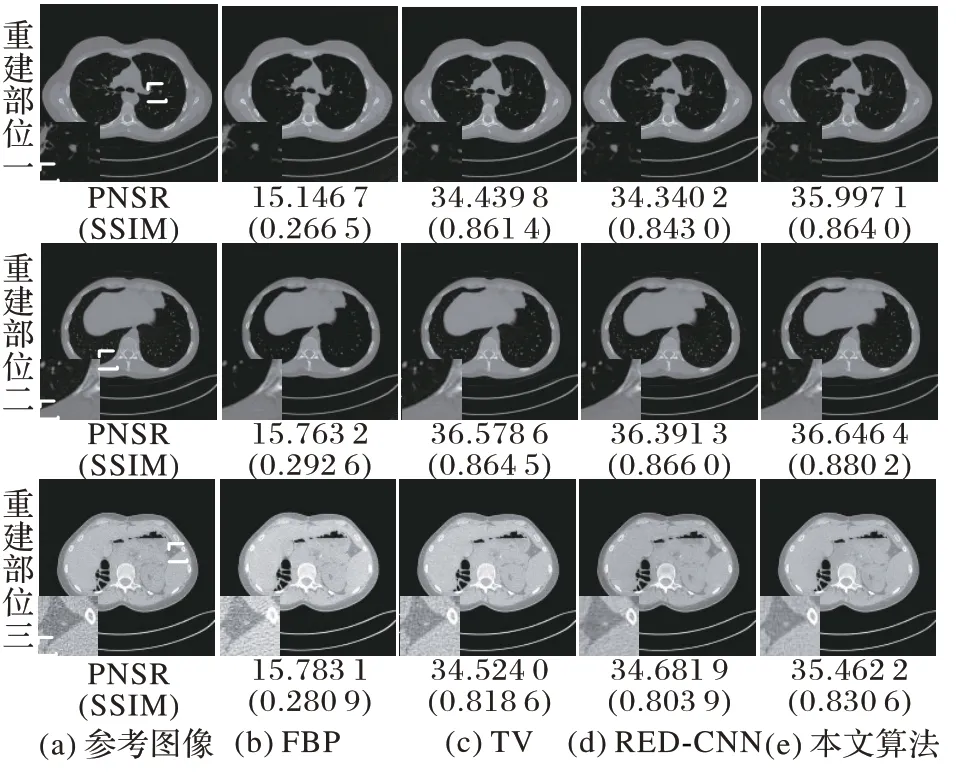
图9 不同算法在投影数目为360时的噪声数据集重建结果对比Fig.9 Comparison of reconstruction results under 360 projections on noisy dataset by different algorithms

从图10 可以看出，与FBP 算法相比，本文算法有效地抑制了重建后图像中条状伪影的产生；与TV算法相比，本文算法进一步抑制了重建后图像中的噪声分布；与RED-CNN算法相比，本文算法很好地保留了重建后图像中的纹理信息。

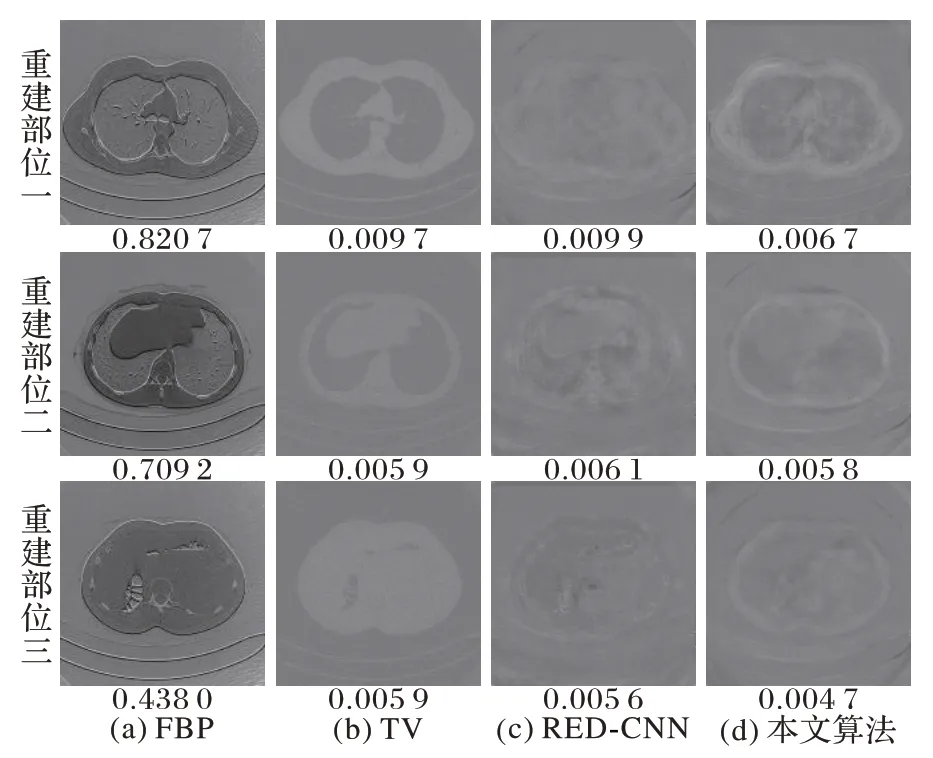
图10 不同算法在投影数目为360时的噪声数据集重建结果残差图Fig.10 Difference images of reconstruction results under 360 projection on noisy dataset by different algorithms

表3 为本文算法与对比算法在360 个投影角度下带噪声测试数据集上的总体表现。从表3 中可以观察到，本文算法的总体评价指标均要优于对比算法，从而表明本文算法在带噪声的数据集上也有很好的表现。

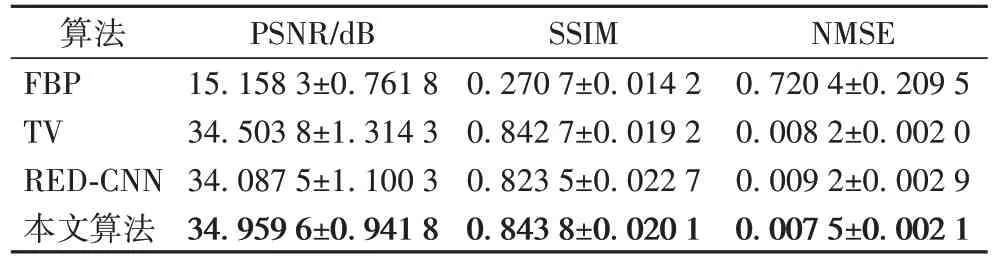
表3 不同算法在360个投影数目下噪声数据集指标对比Tab 3 Index comparison by different algorithms under 360 projections on noisy datasets

5 结语

针对采用传统滤波器进行CT 图像重建，重建后图像存在伪影和图像细节丢失的问题，本文设计了一个端到端的双域CT 重建DDFre-Net，在频域中采用CNN 对投影数据进行滤波，有效地改善了CT 重建图像的质量。为了验证所提算法的有效性，分别在不带噪声数据集和带噪声数据集上，将本文算法与FBP、TV 和RED-CNN 算法进行了比较。实验结果表明，在不带噪声数据集上，所提算法在投影数目分别为180 和90 的情况下重建图像质量高，重建速度快；在带噪声数据及下，所提算法在投影数目为360 的情况下效果最佳。同时DDFre-Net 简单，无需人为设置复杂的超参数，故在实际应用中极易实现。不足之处是DDFre-Net 虽然采用U-Net 的结构减少了参数，但是所需参数仍然较为庞大，可以通过减少U-Net 编解码层的数量进行优化。本文算法针对的是二维扇形束CT 图像重建情形，因为二维扇形束CT 重建是三维锥束CT 重建的一个特例，所以下一步工作将尝试将本文算法向三维锥束适配。