基于自注意力机制时频谱同源特征融合的鸟鸣声分类

刘志华，陈文洁，陈爱斌*

（1.中南林业科技大学计算机与信息工程学院，长沙 410004；2.中南林业科技大学人工智能应用研究所，长沙 410004）

0 引言

近年来，全球工业化快速发展，但同时对环境造成了严重的破坏。许多鸟类失去了原本的栖息地，濒临灭绝，鸟类多样性锐减。各国采取了一系列的举措来保护濒临灭绝的鸟类。保护濒危鸟类的关键一步是先识别出该鸟类，早期识别特定鸟类需要耗费大量的人力资源，如长时间的专家现场观测或根据收集到的录像辨别。

随着人工智能学科的兴起，将人工智能的方法运用到鸟类物种识别，有效减少了人力物力资源的浪费，同时能有效对特定鸟类物种进行识别。鸟类一般生活在茂密的森林，这对于鸟类图像数据的收集造成了一定的困难。虽然使用鸟类图像进行识别的方法取得了一定的成绩，但此类方法有识别范围窄的局限性。而基于音频的鸟鸣声分类在原始数据收集上并没有这一局限性。在真实世界中根据鸟类鸣声录音建立准确的鸟类鸣声分类器是较难的，因为环境噪声的不确定性，鸟类鸣声可能因地理位置而异，音频内容本身也不总是清晰地识别出来。在开放环境中记录的鸟类鸣声往往是嘈杂的，可能有环境噪声、多种鸟类或其他物种的声音同时出现。这些不可避免的复杂问题使得基于音频的鸟类分类富于挑战性。

基于音频的鸟类分类是声学事件分类的一种形式。受益于声学分类，人们对鸟类声音进行了大量的研究。早期的鸟鸣声分类主要以机器学习方法为主，如Qian 等将大规模的鸟类声音特征作为一个极端学习机的输入，证明了人类手工制作的特征用于鸟类识别的高效性。Tan 等采用动态时间规整的算法，将计算得到的鸟鸣声参数与一组参考鸟类鸣声确定的存储模板进行匹配。阙鑫华等改进传统的动态时间规整算法用于鸟鸣声分类，在效果上取得了一定的提升。这种基于模式匹配的方法取得了较好的分类效果；但是由于模式匹配参数获得的局限性，因而限制了该方法的泛化性。隐马尔可夫模型、支持向量机、高斯混合模型等基于鸟类特征的方法被用于鸟鸣声分类。与基于模板匹配的技术相比，此类利用特征进行分类的方法能够更好地推广；但是该类方法对提取鸟鸣声特征在时间和频率上的变化能力有限，难以应对具有嘈杂背景噪声的鸟鸣声分类识别。

最近深度学习被证明比传统的机器学习方法更适合复杂的分类问题。深度学习模型最常用的架构是卷积神经网络（Convolutional Neural Network，CNN），它通过滤波器在特征图的时间和频率维度上同时移位计算来克服机器学习方法特征提取能力不足的局限性。借助短时距傅里叶变换（Short Time Fourier Transform，STFT）等方法将鸟鸣声音频转换为时频谱（Spectrogram），从而CNN 能有效应用于鸟类声音分类。Sprengel 等将鸟鸣声时频谱归一化处理后的结果作为卷积神经网络的输入，在复杂背景下分类的平均精确率（Mean Average Precision，MAP）为0.686。Koops 等在STFT 的基础上对鸟鸣声进一步处理得到更为有效的梅尔频率倒谱系数（Mel Frequency Cepstrum Coefficient，MFCC）作为深度神经网络的输入，该深度神经网络模型用于鸟鸣声分类，MAP 达到了0.73 的分类效果。与使用简单CNN 提取时频特征不同，Sankupellay等使用50层的残差神经网络（Residual Neural Network 50，ResNet50）对鸟鸣声的时频谱进行分类，Huang 等使用稠密连接网络（Densely connected Network，DenseNet）提取时频谱特征并进行分类，提升了分类效果。以上方法均只利用了卷积神经网络的强大特征提取能力对鸟鸣声的时频谱进行特征提取，而大多数的时频谱只包含很少的有价值信息，很多像素是空白的，因此该类方法难以提取到足够的有用信息，在复杂背景噪声情况下表现不佳。

为提取鸟鸣声音频的更多有用信息，出现了一些利用多特征融合的方法。Naranchimeg 等使用视觉特征和声学特征的融合方法在鸟鸣声分类任务上取得了准确率为78.9%的成绩，其结果比使用单一特征分类效果要好。Xie 等选用三种表征鸟鸣声的不同成分：梅尔谱图、基于谐波成分的谱图和基于打击乐成分的谱图，然后选择基于CNN 的模型融合这三类特征得到最终分类结果，达到了86.31%的平均准确率。谢将剑等采用三个独立模型分别提取通过STFT、梅尔倒谱变换和线性调频小波变换得到的鸣声信号特征，然后进行自适应加权融合的结果比任一单通道要好。这些方法的结果证明多特征融合方法的有效性；但与此同时增加了实验样本的数量，而且这种方法忽略了鸟鸣声具有时域连续性特点。

考虑到鸟鸣声具有时域连续性特点。由于循环神经网络擅长捕捉音频的时序特性，Graves 等使用循环神经网络（Recurrent Neural Network，RNN）对语音进行分类。Qiao等基于RNN 提出了一种序列到序列的深度学习方法，该方法从鸟类声音中提取更高级的特征用于分类。这一特点也被用于近年的鸟类跨语言评估论坛（Bird Conference and Labs of the Evaluation Forum，BirdCLEF）挑战赛，2018 年BirdCLEF 挑战赛采用基于RNN 的模型用于鸟鸣声分类，双向长短时记忆（Bidirectional Long Short-Term Memory，BLSTM）结构被应用于文献［29］中。但是RNN 特征提取能力不足，因此刑照亮等采用CNN 加LSTM 方式进行建模，该方法能提取到鸟鸣声的帧间时序信息，有助于提升分类效果。由于3 维卷积神经网络（3 Dimensional CNN，3DCNN）擅长处理时序数据，所以Himawan 等使用3DCNN 提取鸟鸣声时频特征用于分类。Zhang 等在3DCNN 的基础上提出了时频帧线性网络（Spectrogram-frame Linear Network，SPFN）用于分类，在网络前端使用线性3DCNN 提取具有强时域连续性特点的特征，然后在后端采用双重门控循环单元（Gate Recurrent Unit，GRU）作为分类器，该网络能捕捉到鸟鸣声长时间的时域连续性特点。这些利用鸟鸣声的时域连续性特点，提取单一时频谱特征的方法达到了较好的分类效果。但是实时环境下的鸟鸣声特征会存在高频或低频噪声，会和鸟鸣声前景特征混杂在一起。因此仅利用这一特性是不够的，模型的鲁棒性不强。

鸟鸣声本身具有频率高低性特点，且其时频谱是一种描述各个频率成分随时间变化的图像。因此同时关注其时域特性、频域特性以及时频域特性是很有意义的。本文在上述研究的基础上，充分利用鸟鸣声时频谱中所蕴涵的时域特性、频域特性和时频域特性，提出了一种将鸟鸣声时频谱蕴含的三类同源特征进行融合的模型。由于时频谱每一帧的信息在短期内可以认为不变，那么连续的多帧信息就能反映出鸟鸣声长时间内的特点，如其声音的频率范围、时域连续性长度等。本文利用卷积神经网络，采用基于单一向量的卷积滤波器分别在鸟鸣声时频谱的时域维度和频域维度上进行线性移动，同时进行下采样以提取相应维度上的特征信息。最终得到只保留频域或时域维度的两类谱图特征，本文将之分别称为p、t 谱图特征。其中p 谱图特征只拥有鸟鸣声的频域特性，t 谱图特征只拥有鸟鸣声的时域特性。与使用基于单一向量的卷积滤波器不同。本文使用基于多维向量的滤波器在时频谱的时域和频域维度上同时进行移动，得到同时保留时域和频域特性的鸟鸣声特征，本文将之称为pt 谱图特征。自注意力机制能降低其他噪声在特征中的重要性，同时重点关注到鸟鸣声有价值的特征信息。本文提出使用自注意力机制对这三类同源特征进一步处理以加强其各自拥有的特性。最后将t、p、pt 三类同源谱图特征进行决策融合以利用鸟鸣声蕴藏的多种特点，并根据融合后的特征得出最终分类结果。

1 本文模型

本文构建模型用于鸟鸣声分类的工作主要包括以下几个步骤：1）鸟鸣声特征可视化。使用短时距傅里叶变换将鸟鸣声音频信号转化为时频谱图像，再通过梅尔标度滤波器组（Mel-scale filter banks）将时频谱图像转化为梅尔时频谱图像。为增强数据的有效性，本文在该过程中还采取了预加重和对数处理。2）同源谱图特征提取。利用卷积神经网络的特征提取能力，根据三类同源特征的不同特性，设置不同大小的卷积核，在同一时频谱图上进行线性滑动操作得到同源特征。3）特征加强。将自注意力机制和特征融合操作用于三类同源谱图特征，以加强鸟鸣声特征的有效性。4）对提出的模型进行训练和测试。

本文分类模型的具体框架结构如图1 所示。

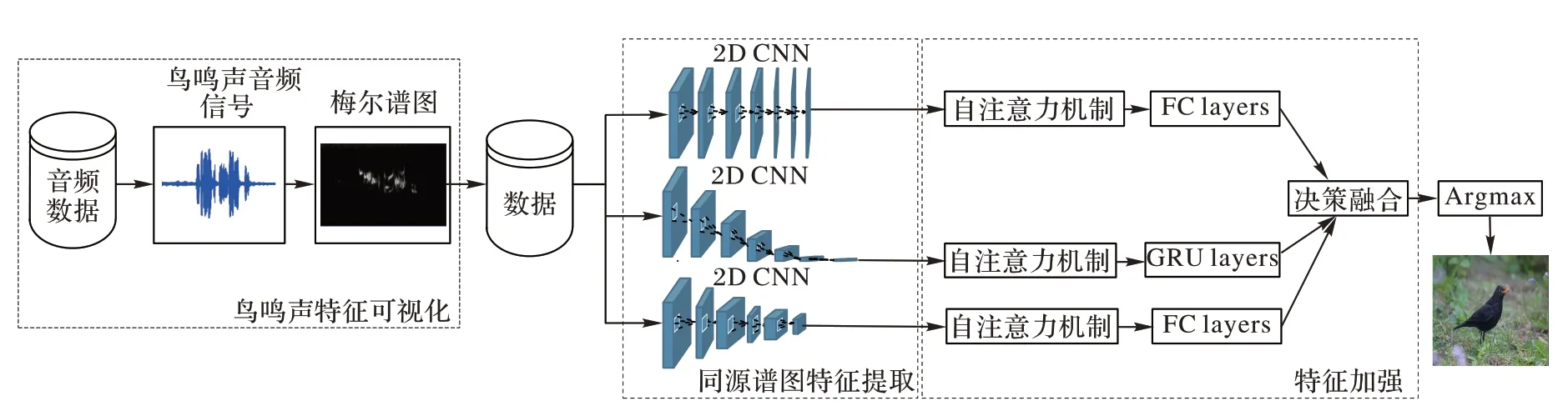
图1 本文分类模型的具体框架结构Fig.1 Specific framework structure of proposed classification model

1.1 鸟鸣声特征可视化

Neal 等已经证实在鸟鸣声分类任务中，将鸟鸣声音频特征可视化是较为有效的。由于信号的傅里叶变换得到的信号频谱不能反映信号瞬时频率随时间的变换情况，仅仅适用于分析平稳的信号。对于非平稳的鸟鸣声音频信号，傅里叶变换只能给出其总体效果，不能完整把握信号在某一时刻的本质特征。因此本文选择短时傅里叶变换来分析鸟鸣声音频信号，它使信号达到局部平稳的同时，能提供时域和频域的局部化信息。为减少音频信号中低频噪声的影响，本文在进行变换之前对原始音频信号进行预加重操作，然后将预加重后的信号再进行短时傅里叶变换得到时频谱。上述两步操作如式（1）～（2）所示：

其中：

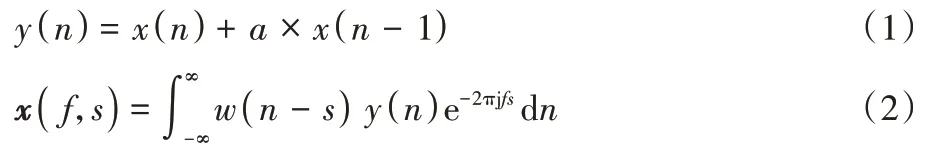
x

(

n

)是第

n

时刻的信号采样值；

a

是预加重系数，一般为0.95；

y

(

n

)是预加重后的信号采样值；

w

(

n

-

s

)是汉明窗（Hamming window），其中心位置在

s

处。参考文献［36］的设置，文中的汉明窗长度为1 024 即一窗内包含1 024 个采样点值，步长为512 即帧移率为50%。

x

()

f

，

s

是经过短时傅里叶变换后得到的二维时频谱矩阵；

f

是矩阵的行数，表示频率；

s

是在每个窗口内变换得到的帧。本文参照文献［19］将原始音频标准化为约7 s，可得帧数

s

取值属于［0，600），滤波器个数设置为80，可得

f

取值属于［0，80）。最终可以将鸟鸣声特征可视化为80×600 的图像。将时频谱矩阵

x

()

f

，

s

通过梅尔标度滤波器组（Mel-scale filter banks）便能得到梅尔时频谱

x

(

fmel

，

s

)，具体实现如式（3）所示：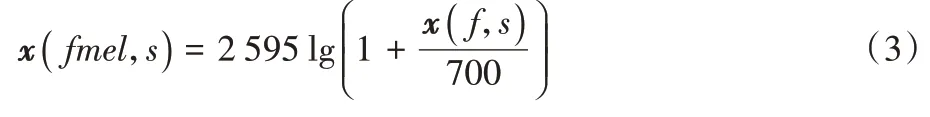

而将幅度值进行对数操作可以进一步加大高低振幅的区别，有助于提取鸟鸣声有用信息。因此最后将幅度值取对数操作，将其转换成对数幅度。经过上述处理后，可以得到鸟鸣声音频特征的可视化图，如图2 所示。

图2 大小为80×600的鸟鸣声特征可视化Fig.2 Visualization of bird sound features with size of 80×600

1.2 同源谱图特征提取

为利用鸟鸣声时域连续性特点，文献［2，31］使用循环神经网络直接从时频谱中提取特征用于分类。研究表明循环神经网络在特征提取上有一定的局限性，如对时频谱图特征的扩充和预处理难以实现。而卷积神经网络拥有强大的特征提取能力，将其作为循环神经网络的前置特征提取器能提升分类效果。

基于此，本文采用2 维卷积神经网络（2 Dimensional CNN，2DCNN）来提取鸟鸣声时频谱中蕴藏的t、p、pt 三类同源特征信息。根据三类同源谱图特征信息的特点，分别使用基于单维向量和多维向量的卷积核用于三类同源谱图特征的提取。t 谱图特征具有鸟鸣声完整的时域连续性特点。因此采用大小为［

N

，1］的单向量卷积核在谱图上不断上下滑动，并使用［

N

，1］的池化核进行下采样操作，直到其频域维度降为1 为止。最终将当前时间步上所有高频至低频的信息融合到一起，并按时间顺序排序堆叠。与提取t 谱图特征的操作不同。对于只表现鸟鸣声频域特点的p 谱图特征，本文使用大小为［1，

M

］的单向量卷积核在时频谱图上不断左右滑动，使用大小为［1，

M

］的池化核在时频谱的时间维度上进行下采样操作。最终原始时频谱图的时域维度降至一维。时频谱连续帧的所有信息均融合到对应的频率维度，只保留完整的频域特性。上述操作的优点是不会破坏鸟鸣声时域连续性或频域高低特点，且能提取到鸟鸣声特征在时域上或频域上细微的变化。对于pt 谱图特征，考虑到其同时拥有鸟鸣声时域和频域特点，本文综合提取p、t 谱图特征的设置，采取大小为［

M

，

N

］的多维向量卷积核，在时频谱的时域和频域维度上同步滑动以保留其原本具备的时频特性；同时使用大小为［

M

，

N

］的池化核进行下采样操作，最终得到具有时频特性的pt 谱图特征。提取t、p、pt 特征的网络各层参数设置分别如表1～3 所示，其中滤波器个数为8 的层是卷积层，其余为池化层。经过上述操作后得到t、p、pt 谱图特征，其大小分别为1×600、80×1、9×25。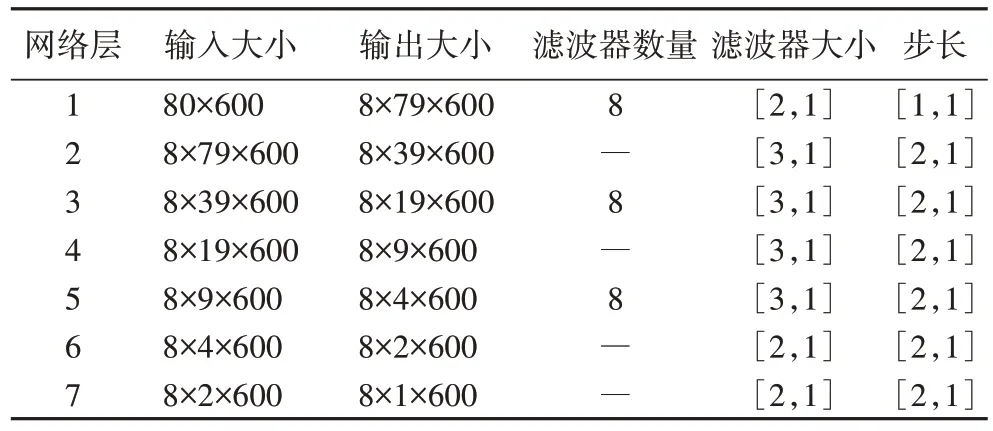

表1 提取t特征的网络参数设置Tab 1 Parameter settings of the network to extract t feature

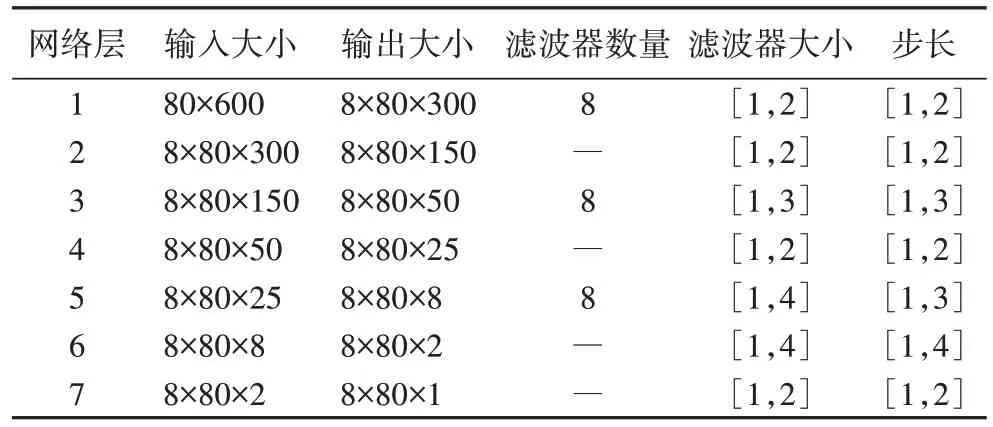
表2 提取p特征的网络参数设置Tab 2 Parameter settings of the network to extract p feature

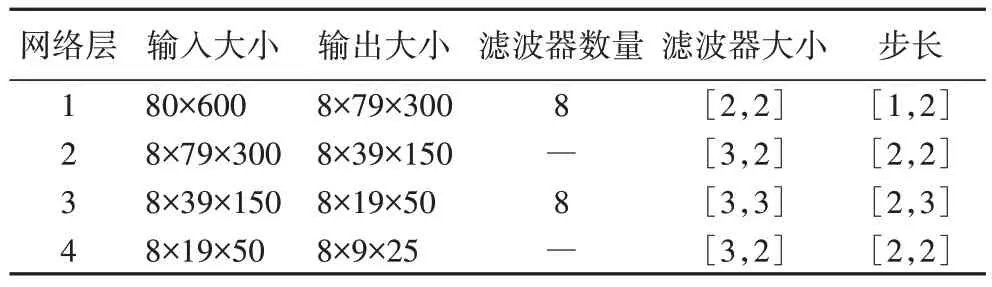
表3 提取pt特征的网络参数设置Tab 3 Parameter settings of the network to extract pt feature

1.3 特征加强

由于卷积神经网络在提取t、p、pt 谱图特征时候，有些噪声如高频或者低频噪声可能会被过多地关注。这会降低鸟鸣声特征的有效性。

自注意力机制能加强想关注的部分特征。在文献［43］中提出了一种具有时间关注的CNN-BLSTM 模型来加强对音频特征的关注，其注意力根据每一层卷积神经网络提取的特征计算而来，且不影响特征本身的提取。因此本文模型采用自注意力机制来加强对鸟鸣声特征的关注，同时降低噪声的重要性，进而提高鸟鸣声音频特征的有效性。为不增加网络的复杂度，本文仅对每一个通道最后一层池化后得到的谱图特征采取自注意操作。由于三类同源谱图特征的维度不一致，因此使用自注意力机制分别关注t、p、pt 谱图特征，而不是使用同一注意力机制参数关注不同的特征。自注意力机制的具体实现方法如式（4）～（6）所示：

其中：

query

、

key

、

value

是当前的谱图特征经过1×1 卷积后得到的特征矩阵，与原始谱图特征形状一致；

Score

是

query

和

key

特征矩阵点乘后得到的结果；

n

是特征矩阵中数值点的个数；

S

是根据当前

Score

元素经过计算得到的注意力权重值；

S

是

S

按照在原特征矩阵中的位置组合得到注意力权重矩阵；

output

是谱图特征和注意力权值相乘后得到的结果。

经过上述操作，可以得到加强的p、t、pt 同源谱图特征。本文将这三类谱图特征分别作为分类器的输入，然后将三个分类器的输出得分进行决策融合，对特征进一步地加强。在具体操作上，将这三个分类器的输出类别得分进行一个简单的相加，然后取平均值操作。因为分类器输出结果是对当前鸟鸣声预测为某一类别的概率值，所以对相加后的结果取平均值操作，以防止对每个类别的预测概率得分超过上限值1。决策融合具体实现如式（7）所示：

其中：

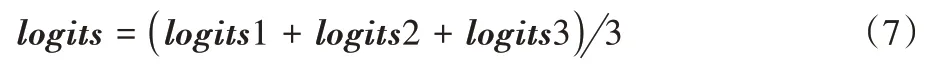
logits

1、

logits

2、

logits

3 是三个通道根据三类同源特征的预测得分；

logoits

是所有预测得分融合后的结果。将决策融合后的结果通过Argmax（）函数，可以得到鸟鸣声分类的结果。本文选用不同的分类器用于三类同源谱图特征的分类：对于p、pt 谱图特征，选用全连接层（Fully Connected layers，FC）作为分类器；对于t 谱图特征，考虑到其具有完整的时间连续性特点，因此并没有使用全连接层作为分类器，而是使用擅长处理时序信号的循环神经网络用于分类。在具体的循环神经网络选择上，本文选用GRU 网络，这是因为GRU 网络比长短时记忆（Long Short-Term Memory，LSTM）网络更易于训练，且分类效果相差无几。

2 实验与结果分析

2.1 实验数据

本文使用自动脚本程序从鸟类公共数据集Xeno-canto网站获取所需要的鸟类音频数据，这些音频采样率为48 kHz且均以MP3 格式保存。生物等级分类依次是界、门、纲、目、科、属、种。本文从该网站中选取灰雁、普通鵟、金黄鹂、喜鹊、乌鸫、叽喳柳莺、欧柳莺、大山雀这八种鸟类（其学名分别为Anser anser、Buteo buteo、Oriolus oriolus、Pica pica、Turdus merula、Phylloscopus collybita、Phylloscopus trochilus、Parus major），其中欧柳莺、叽喳柳莺是同一属下的不同种类，其他六种鸟类均为分属于不同科下的鸟类。灰雁属于鸭科，喜鹊属于鸦科，普通鵟属于鹰科，金黄鹂属于黄鹂科，大山雀属于山雀科，欧柳莺和叽喳柳莺属于柳莺科，乌鸫属于鸫科。这八种鸟类的音频均由世界各地的人们自愿上传到该网站，本文选用的这八种鸟类是经过科学考虑的，首先这八种鸟类在该网站中的音频数据是相对较多的；其次这八种鸟类中有些鸟类生活在茂密的森林中，其栖息地物种繁多，对生物多样性的鉴别也有一定的意义；此外这些鸟鸣声包含与鸟鸣声相互混杂的复杂背景噪声，且同一属下的鸟类鸣声比较相似，不同科下的鸟鸣声相似性不大。因此本文随机选取自然情况下录制的这八种鸟类音频进行实验，以验证本文提出的模型的泛化性以及鲁棒性。由于原始音频录制时间长短不一，为了将输送进网络的数据标准化，本文将原始音频切分为多个互不重叠的片段（约7 s）。这样每个原始音频可以得到多个实验样本，并能较好地扩充数据集。本文所采用的八种鸟类的鸣叫声特征图如图3 所示。

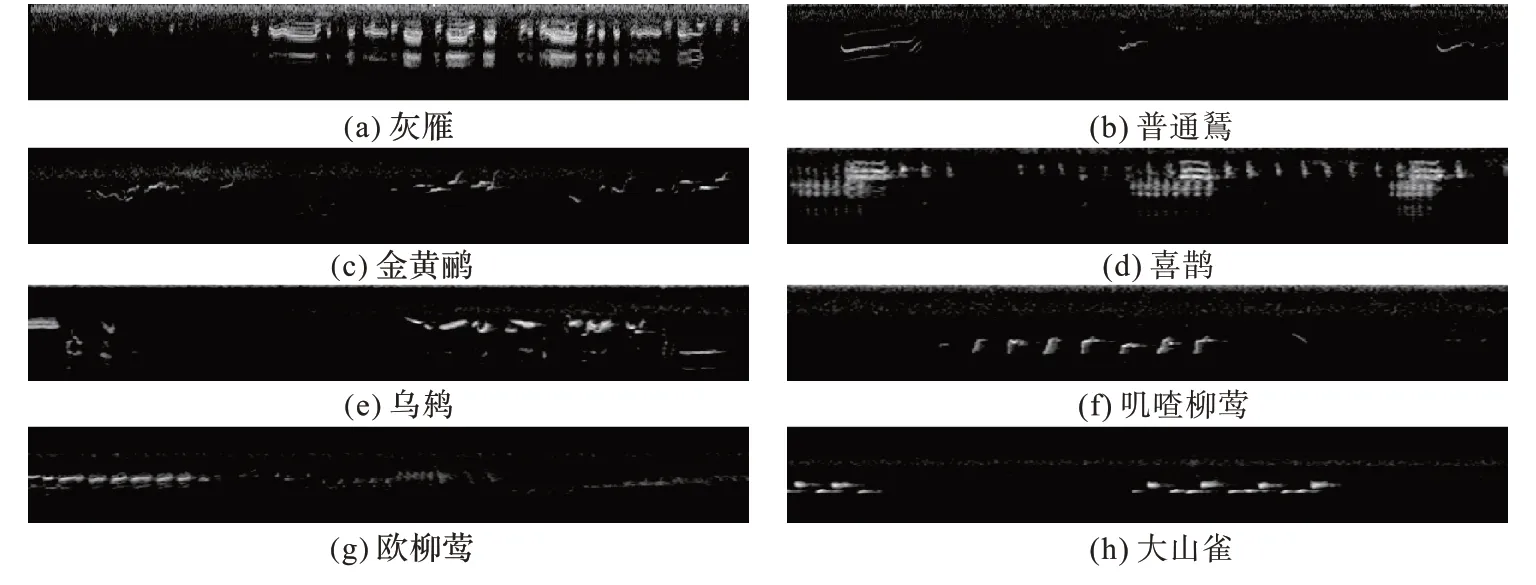
图3 八种鸟类的鸟鸣声特征图Fig.3 Bird sound feature pictures of the eight bird species

在长时间的音频段中鸟鸣声片段较短，标准化后得到的实验样本并不都包含鸟鸣声特征，有些样本可能只包含一些纯粹的背景噪声或包含其他鸟类的声音，这些情况导致有些实验样本的标签与实际标签不符合，对分类效果会造成不好的影响。因此需要重新标记，去掉只有噪声或者空白的样本。与完全利用人工的操作方式不同。本文先利用基于能量比对的算法进行一个初步筛选，以减少后期人工操作的工作量。本文从每一类的实验样本中挑选一个基本没有噪声的数据作为该类实验样本的基线，计算该样本中所包含的能量总和。然后遍历该类中所有的实验样本，如果当前实验样本能量低于基线样本能量总，则将当前实验样本删除。

经过上述操作，本文选用的这八种鸟类的原始音频数量以及最终的实验样本数量如表4 所示。

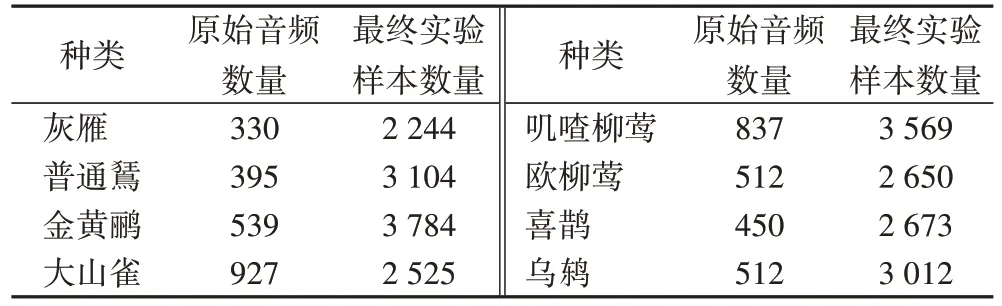
表4 每种鸟类的实验样本数量Tab 4 Number of experimental samples per bird species

2.2 模型训练

在每一次的实验中，训练集和测试集不是固定的。而是按照7∶3 的比例将所有实验样本随机划分为训练集和测试集，随机得到的训练集样本16 493 个，测试集样为7 068 个。本文实验代码建立在Tensorflow1.14.0 框架基础上，Python环境为3.6.8，硬件环境为Intel i9，Nvidia Titan XP。根据实验环境的硬件条件，本文一次选取16 个实验样本进行实验。综合考虑文献［44-46］的做法，本文使用均方根传递（Root Mean Square Prop，RMSProp）梯度下降优化算法作为网络的梯度优化方法，将动量参数设置为0.7。本文采用MAP 作为分类预测效果指标，交叉熵（cross entropy）损失函数作为网络的损失衡量函数，损失函数具体如式（8）所示：

其中：

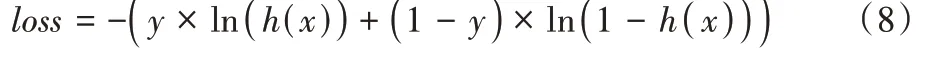
loss

是当前的损失值；

y

是当前预测结果为假或真的情况，对应值为0 或1；

h

(

x

)是当前样本

x

为真或假的概率值。为防止网络的过拟合，在每一个卷积层采取正则化操作。训练时在卷积层和分类器之间采取随即失活策略，且随机失活率

drop_rate

=0.3，而测试时

drop_rate

=0。最终采用可变学习率函数来进行训练，模型的初始学习率设置为0.001。根据多次实验结果，可以认定该学习率函数适合于本文的模型和数据集。学习率函数具体如式（9）所示：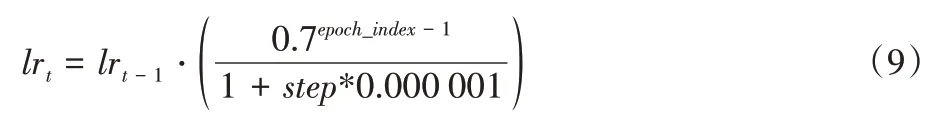

其中：

lr

是第

t

次迭代后得到的学习率，

lr

是其初值，具体值为0.001；

epoch

_

index

是数据训练的次数，根据多次实验，本文将其训练次数设置为30；

step

代表当前是第几次迭代，每次迭代就会更新一次参数。

2.3 结果分析

本文提出的模型在训练数据集上表现良好。经过30 个epoch 训练后接近过拟合，此时停止训练并保存模型参数，随后将训练得到的模型参数用于测试集数据，得到最终预测结果。在实验中，本文将模型训练和测试的相关数据保存以供分析。将训练的预测准确率值和损失值相关数据可视化，如图4 所示。对图4 进行分析，可以知道本文模型在训练初始，其准确率曲线先快速上升，而后缓慢上升，最后趋于不变。同样分析可以得到本文模型的损失在训练初始快速下降，而后缓慢下降，最后趋于不变，稳定在0.127 附近。在训练初始，本文模型的损失和准确率曲线波动幅度较大，但是随着训练的增加而快速趋于稳定。由此可以确信提出的这个模型能够快速学习到鸟鸣声三种同源谱图特征具有的特点，所以能很好地应对复杂背景噪声干扰。

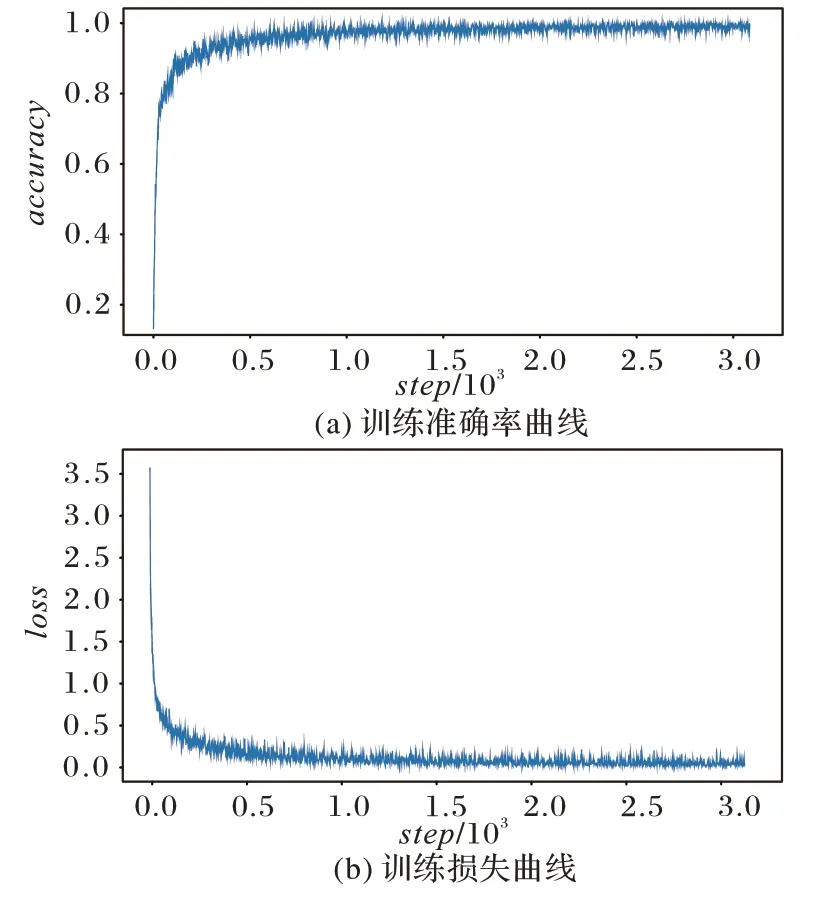
图4 训练数据可视化Fig.4 Visualization of train data

将测试的预测准确率值和损失值相关数据可视化，如图5 所示。对图5 所示结果进行分析可知，本文模型的鸟鸣声识别准确率稳定在0.939，损失稳定在0.127 左右，且波动均在合理范围内。测试准确率和训练准确率稳定后的差值在0.024～0.030，相应的损失差值在0.001～0.004。在实验样本包含各种复杂背景噪声的情况下，本文模型也能达到较好的效果，可以证明从同一鸟鸣声时频谱中提取p、t、pt 三类同源谱图特征进行融合的有效性。本文模型能够有效学习到鸟鸣声在时域、频域和时频域上的一些抽象规律。

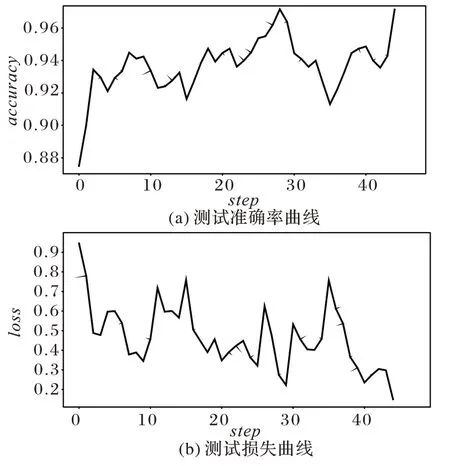
图5 测试数据可视化Fig.5 Visualization of test data

为了更好验证所提模型的有效性，进行了一系列的自对比实验。实验结果如表5 所示。

在表5 的实验1～3 中，分别以鸟鸣声所具有的不同特性作为分类依据。实验1 将鸟鸣声的频域高低性特点用于分类，分类准确率为0.896，在这三个实验中效果最佳。实验2利用鸟鸣声时域连续性特点用于分类，识别效果仅只有0.804。实验3 利用结合鸟鸣声的时频特性用于分类，效果仅次于利用其频域特性用于分类的模型，其分类效果为0.872。综合实验1～3 的结果，本文认为在具有复杂背景噪声的情况下，鸟鸣声频域特点能较好反映出鸟鸣声的抽象规律；而当背景噪声在整个时域上都存在的时候，噪声会和鸟鸣声真实特征混合，造成伪连续性现象，导致模型学习鸟鸣声连续性特点较难，因此实验2 的分类效果较差。

表5 自对比实验结果Tab 5 Self-comparison experiment results

表5 中的实验4，利用了鸟鸣声具有的时域、频域、时频域特性，提取t、p、pt 同源谱图特征进行决策融合（Decisionfusion）的结果用于分类，达到了较好的效果。本文认为三类同源特征能够互补，所以决策融合能加强特征的有效性，在复杂背景噪声下表现出较好的鲁棒性，其分类效果为0.923。实验4 比实验1 的分类效果提升了2.7 个百分点，这也证明了本文提出利用鸟鸣声蕴藏的三类固有特性用于分类的有效性。实验5 在实验4 的基础上，引入了自注意力（Self-attention）机制。在同样的情况下，取得了平均准确率为0.939 的分类效果。实验5 较实验4 的分类准确率提升了1.6 个百分点，较实验1 利用鸟鸣声频域特性用于分类的准确率提升了4.3 个百分点。这证明了注意力机制可以加强提取到的t、p、pt 同源谱图特征，能够让本文的模型学习到鸟鸣声更多细腻的抽象规律，也证明了引入自注意力机制的正确性。

本文对模型的性能进行了更加细腻的分析。根据测试集每一个样本的预测和真实标签，绘制出8 分类的混淆矩阵如图6 所示。其中矩阵的行代表真实的标签，列代表本文模型预测的分类标签。

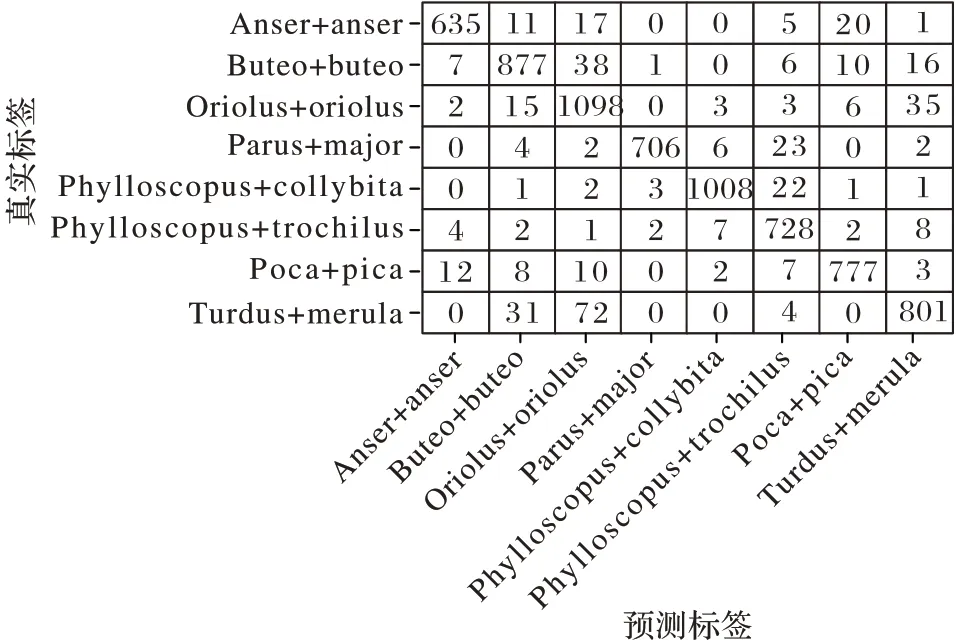
图6 测试集的混淆矩阵Fig.6 Confusion matrix of test set

对混淆矩阵进行分析，可以得到模型对每一种鸟类更确切的数据，如精确率（Precision）、召回率（Recall）、

F

1 值（F1-score）等。将这些数据统一展现在表格中，如表6 所示。其中精确率（Precision）和召回率（Recall）是广泛应用于信息检索和统计学分类领域的两个度量值，用来评价结果的质量。精确率体现了预测为正的样本中有多少是真正的正样本。MAP 是8 种类别精确率的平均值，本文的MAP 为0.939。召回率体现的是样本中的正例有多少被正确预测了。F1-score 是综合精确率和召回率的评价指标，用于反映模型整体效果的指标，且其分数值越接近1，说明模型的分类效果越好。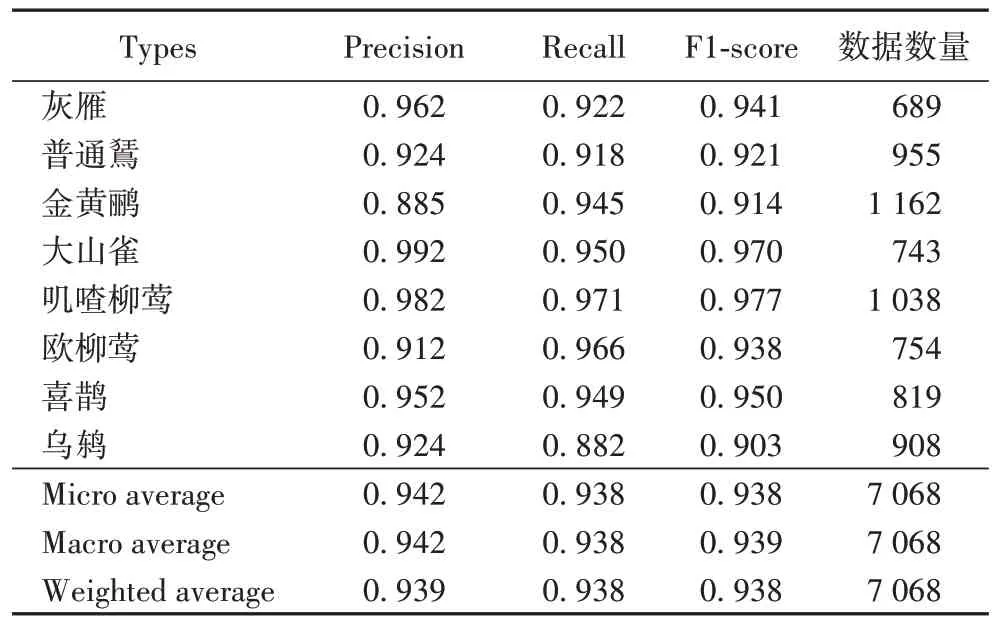

表6 混淆矩阵分析结果Tab 6 Confusion matrix analysis results

回顾图4 可以看到，灰雁的实验数据混杂了大量的高频噪声。本文模型对灰雁的分类准确率达到了0.962，且其F1-score 也较高为0.941，证明了本文模型抗噪性较强；然而对金黄鹂的分类精确率仅为0.885，观察实验数据发现该类实验样本不仅包含大量的背景噪声，同时还夹杂着其他鸟类的鸣叫声。本文认为共生鸟的鸣叫声，在频率上和金黄鹂鸣叫声较为相近，困扰了本文模型对特征的提取。但是与表5中实验1 利用p 谱图特征进行分类的结果相比。本文的模型对金黄鹂的分类精确率依然提升了3.3 个百分点（限于篇幅，并未在此处将表5 实验1 的混杂矩阵展示），且其F1-score仍然较高为0.914，证明了本文模型还能应对非目标鸟鸣声噪声的影响。从图4 中可以看到，灰雁和喜鹊、叽喳柳莺和欧柳莺的叫声比较相似，但这四种鸟类的分类精确率均在0.91 以上，F1-score 在0.93 以上，这说明本文模型对细腻度下的鸟鸣声分类依然有效。灰雁和欧柳莺的F1-score 较低，这并不能说明本文模型对于细腻度下得分类存在缺陷。本文认为这是该两类训练数据集比其他两类较少造成的。综合上述分析，本文认为提出的模型方法能够应对复杂背景噪声下的鸟鸣声分类问题。

在同一数据集上，本文还与其他模型进行对比实验，评价指标使用MAP。实验结果如表7 所示。从表7 中可以看到，实验1 的MAP 只有0.872，效果较差。这说明了前文的猜想即简单提取鸟鸣声特征，难以应对复杂的背景噪声。实验2 和实验3 均利用了鸟鸣声时域连续性特点，实验3 分类效果的MAP 为0.932，这验证了利用鸟鸣声时域连续性特点的有效性。但是实验3 的MAP 仅为0.868，本文认为这是因为循环神经网络在特征提取上有一定的局限性，验证了文献［39-40］的结论。本文模型在对比实验中取得了较好的成绩，MAP 为0.939。这验证了本文利用鸟鸣声固有的特性用于分类的有效性，能够应对复杂背景噪声下的鸟鸣声分类，模型具有较强的抗噪性以及泛化性。

表7 与其他模型对比实验结果Tab 7 Comparison of experimental results with other models

3 结语

本文利用鸟鸣声的时域连续性和频域高低性，以及时频域既连续又有高低性特点，提出了从同一张时频谱中分别提取鸟鸣声的t、p、pt 谱图特征。采取自注意力机制和特征融合操作加强鸟鸣声特征的有效性，然后将融合后的结果用于分类。经过科学考虑，本文从Xeno-canto 网站上选取了具有代表性的8 种鸟类。这些鸟鸣声音频大都包含了复杂背景噪声如混杂的非目标鸟鸣声、风声等，且有些鸟类鸣叫声较为相似。本文模型取得了MAP 为0.939 的较好分类效果。实验结果验证了本文模型的优越性，在复杂背景噪声下仍然能较好地学习到鸟鸣声抽象规律。未来的研究将致力于提升鸟鸣声分类效果，同时增强模型的抗噪性：继续研究鸟鸣声本身所具有的一些特性，并探究其利用模型；研发较好的噪声去除模型以减少噪声对分类效果的影响，如充斥在整个时间域上的噪声或者和鸟鸣声混杂在一起的高低频噪声等。