基于局部冗余混合编码的故障快速恢复方法

刘靖宇，牛秋霞，李萧言，史巧硕，武优西

（河北工业大学人工智能与数据科学学院，天津 300401）

0 引言

近年来，新产生的数据量呈艾字节（Exa Byte，EB）增长，研究表明全球数据总量将在2030 年达到2 500 ZB。磁盘以大容量、低成本的优点作为海量存储系统的存储介质，但磁盘故障频发，对金融、军事等各个领域产生了严重影响，因此如何满足存储可靠性要求具有重要意义。

独立磁盘冗余阵列（Redundant Array of Independent Disks，RAID）为海量数据的存储提供了可靠性保障，得到了广泛应用。由于校验阵列码的重构性能可由存取数据块的个数来衡量，基于非最大距离可分（Non-Maximum-Distance-Separable，Non-MDS）码的RAID6 在重构过程中重构链较短，重构失效数据块读取更少的数据量，因此提升了重构性能，越来越受研究人员关注。如：WEAVER 编码、HoVer 编码、Code-M（

s

，

c

）。WEAVER 编码可容多盘故障，缺点是存储效率低；HoVer 编码的重构性能不稳定；Code-M（

s

，

c

）在重构时，要读取其他条带单元组的大量数据，重构读开销大。针对现有Non-MDS 编码重构时间有待减少的缺陷，基于Code-M（

s

，

c

）中条带单元组的概念，提出一种支持故障快速恢复的Non-MDS 编码：局部冗余混合编码Code-LM（

s

，

c

），其与Code-M（

s

，

c

）的主要差异如下：1）Code-LM（

s

，

c

）牺牲了一定存储空间，在每个条带单元组中增加了局部冗余：组内水平校验块，进一步缩小了重构链长度，减少了重构失效数据块所需读取数据量，提高了重构性能。2）水平对角校验块的生成方法不同。Code-M（

s

，

c

）中任意水平对角校验块有且只有1 种生成方式，Code-LM（

s

，

c

）中任意水平对角校验块与任意组内水平校验块均有2 种生成方式。3）恢复失效数据块方式不同。Code-M（

s

，

c

）恢复任意失效数据块有2 种方式，Code-LM（

s

，

c

）恢复任意失效数据块有4 种方式，Code-LM（

s

，

c

）不同数据块的重构链存在公共块，减少了重构时读取的数据量。4）Code-LM（

s

，

c

）提高了存储系统容错性。条带单元组均出现单盘故障时，Code-M（

s

，

c

）不可恢复，Code-LM（

s

，

c

）可恢复。

1 相关工作

1988 年，Patterson 等提出了RAID 技术，RAID 以数据条带化提升了系统性能，以数据冗余机制提升了数据可靠性。RAID 结构通常被划分为RAID0 到RAID6。其中，RAID0 存储效率（数据块的数目与所有块的数目的比值）为100%，但不具备容错能力；RAID1 通过镜像方式实现数据冗余，但存储效率低；RAID4 和RAID5可容单个盘故障，RAID6 可容忍任意双盘故障。随着存储规模增大，磁盘故障频发，为提高存储系统可靠性，RAID6 的使用日益广泛。

副本与阵列纠删码是RAID6 常用的两种保障存储可靠性的方法，与副本相比，阵列纠删码存储效率更高。根据MDS 特性，阵列纠删码分为最大距离可分（Maximum-Distance-Separable，MDS）编码和Non-MDS 编码。MDS 编码校验块为全局校验块，重构链长度随着存储系统规模增大而增加，重构性能下降，如EVENODD 编码、RDP（Row-Diagonal Parity）编码、N 编码、Short 编码、HV（Horizontal-Vertical）编码等。与MDS 编码相比，Non-MDS编码分布了更多的校验块，缩小了重构链的长度，重构失效数据块所需数据量较少，重构性能与存储系统规模无关。根据存储效率的不同，Non-MDS 编码分为两类：存储效率大于50%，如HoVer 编码、Code-M（

s

，

c

）、V-Code（

m

，

n

）；存储效率低于50%，如WEAVER 编码。

WEAVER 编码是具有对称形式的垂直编码，最多能容12 盘故障，缺点是存储效率低，在绝大多数配置下低于50%。HoVer 编码存在两种长度的校验链，分别为水平校验链与对角校验链，如图1 所示。其重构性能不稳定：当故障两个磁盘的编号间距较大时，重构效率高；当故障的磁盘为水平校验盘或故障的两个磁盘编号相邻时，重构性能低。

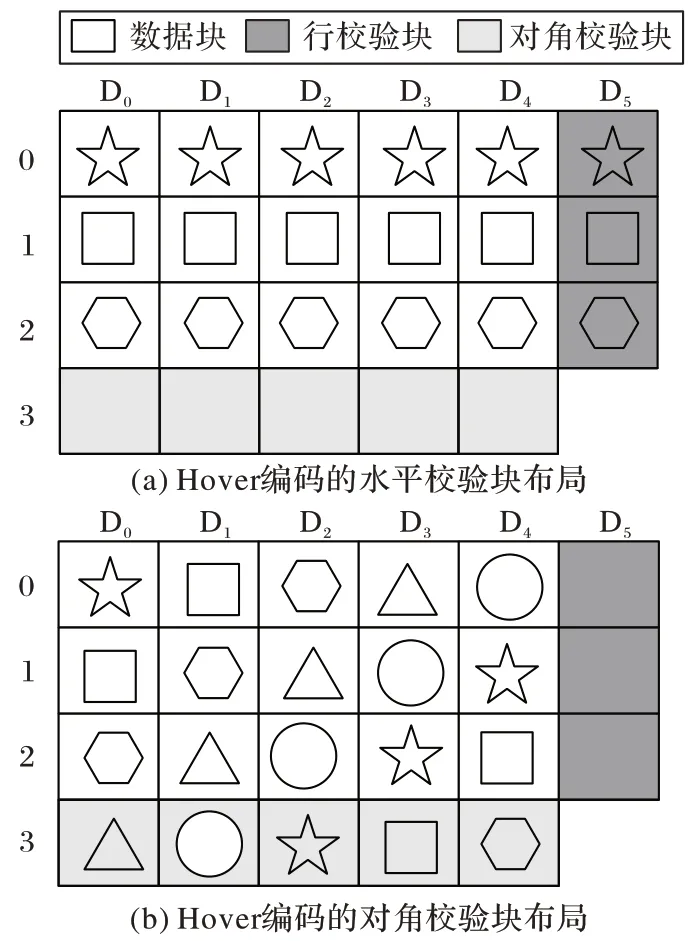
图1 HoVer编码的校验布局Fig.1 Parity layout of HoVer code

D、D、D、D、D、D表示阵列中的6 块磁盘，行校验块存储在水平校验盘D，若D失效，重构时需要读取所有磁盘的全部数据，如图1（a）所示。Code-M（

s

，

c

）引入了条带单元组的概念，根据不同的故障情况采取对应的重构方法。Code-M（

s

，

c

）存在以下不足之处：1）重构时，要读取序号相邻的条带单元组的大量数据，读开销较大，重构时间有待减少；2）容错能力有待提升，例如当每个条带单元组均存在一个故障磁盘时，故障不可恢复。

谢平提出设计新型高容错能力的Non-MDS 编码成为提高重构性能的一种研究趋势，因此通过减少重构链链长来减少重构过程中存取数据块的个数，对于提高存储系统重构性能具有重要意义。

2 Code-LM（s，c）编码

Code-LM（

s

，

c

）中

s

表示每个条带中条带单元组的数目，

c

表示每个条带单元组中条带单元的数目，每个条带单元有

c

+1 个连续的块。为具有双盘容错能力，

s

不小于2，

c

+1 为大于等于5 的质数。

2.1 数据块与校验块的分布

二元组（

s

，

c

）表示特定的条带单元，该条带单元所在条带单元组的序号为

s

，且

s

满足0 ≤

s

≤

s

-1；该条带单元在条带单元组

s

中的列号为

c

，且

c

满足0 ≤

c

≤

c

-1。三元组(

s

，

r

，

c

)表示条带单元(

s

，

c

)上的特定块，该块在条带单元(

s

，

c

)中的行号为

r

，且

r

满足0 ≤

r

≤

c

。

基于Code-LM（3，4）的RAID 分组中，每个条带有3 个条带单元组，分别标记为条带单元组0，条带单元组1，条带单元组2；每个条带单元组有5 行，分别标记为0，1，2，3，4；每个条带单元组有4 列，每列对应一个条带单元，如在条带单元组0 中有4 个条带单元，分别标记为（0，0），（0，1），（0，2），（0，3）；每个条带单元有5 个块，如条带单元（0，1）中的5 个块可分别标记为（0，0，1），（0，1，1），（0，2，1），（0，3，1），（0，4，1），如图2 所示。

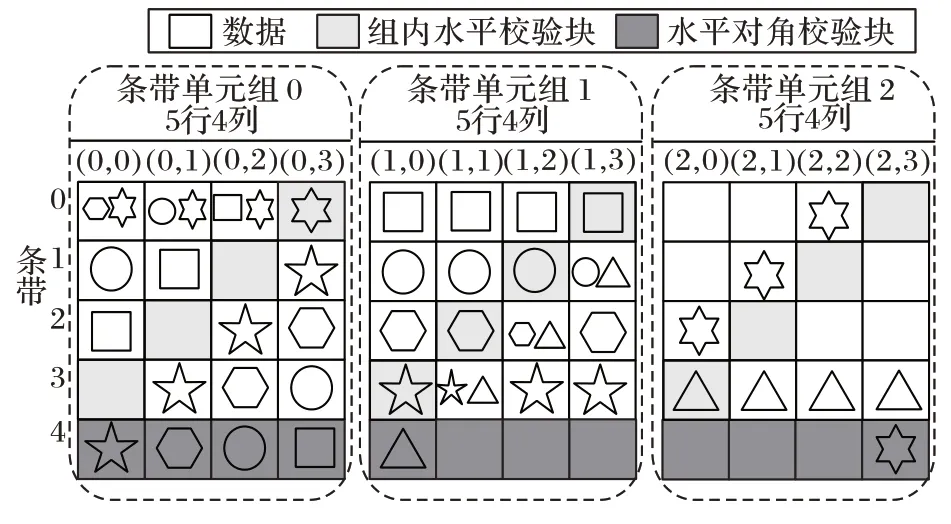
图2 Code-LM（3，4）的校验布局Fig.2 Parity layout of Code-LM（3，4）

对于Code-LM（

s

，

c

）中的块(

s

，

r

，

c

)，当

r

+

c

=

c

-1，(

s

，

r

，

c

)为组内水平校验块；当

r

=

c

，(

s

，

r

，

c

)为水平对角校验块，其余块为数据块。条带单元（0，3）中组内水平校验块为（0，0，3），水平对角校验块为（0，4，3），数据块为（0，1，3），（0，2，3），（0，3，3）。

形状相同的块处于同一校验链。例如在条带单元组0中，处于行序号为0 中的数据块（0，0，0），（0，0，1），（0，0，2）与在条带单元组2 中同一对角线上的块（2，2，0），（2，1，1），（2，0，2），（2，4，3）构成同一水平对角校验链。

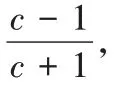
2.2 Code-LM（s，c）的构建规则

Code-LM（

s

，

c

）中的任意一个数据块参与三个校验块的生成，分别为1 个组内水平校验块，2 个水平对角校验块。任意组内水平校验块()

s

，

r

，

c

有两种生成方式：1）由条带单元组

s

中同一行上的数据块异或生成，形式化编码规则如式（1）；2）由条带单元组()

s

-1 mod

s

中的一组对角线上的块异或生成，形式化编码规则如式（2）。任意水平对角校验块(

s

，

r

，

c

)有两种生成方式：1）由条带单元组

s

中的一组对角线上的数据块与条带单元组(

s

+1)mod

s

中的同一行上的数据块异或生成，形式化编码规则如式（3）；2）由条带单元组

s

中的一组对角线上的数据块与条带单元组(

s

+1) mod

s

中一个组内水平校验块异或生成，形式化编码规则如式（4）。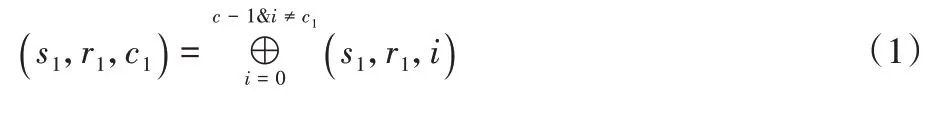

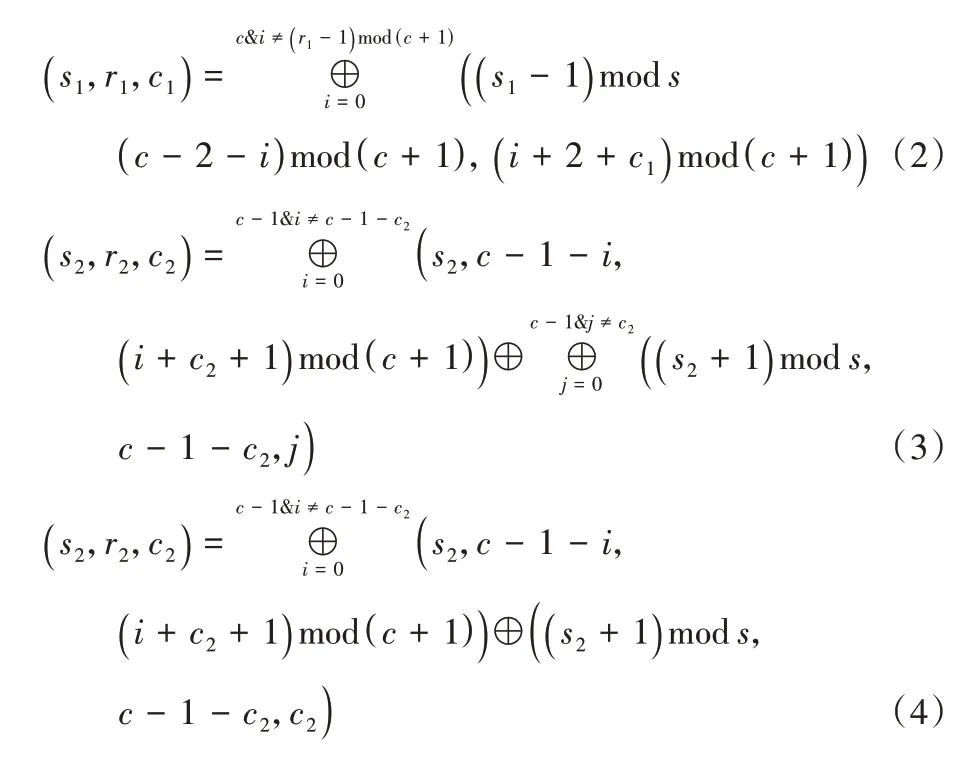
2.3 Code-LM（s，c）的重构方法

任意一个失效的数据块(

s

，

r

，

c

)有4 种恢复方法：1）由条带单元组

s

中的同一行上的数据块与组内水平校验块异或生成，重构规则如式（5）；2）由条带单元组

s

中的同一行上的数据块与条带单元组(

s

-1) mod

s

中的一组对角线上的块异或生成，重构规则如式（6）；3）由条带单元组

s

的一组对角线上的块与条带单元组(

s

+1) mod

s

中的一个组内水平校验块异或生成，重构规则如式（7）；4）由条带单元组

s

中的一组对角线上的块与条带单元组(

s

+1) mod

s

中的同一行上的数据块异或生成，重构规则如式（8）。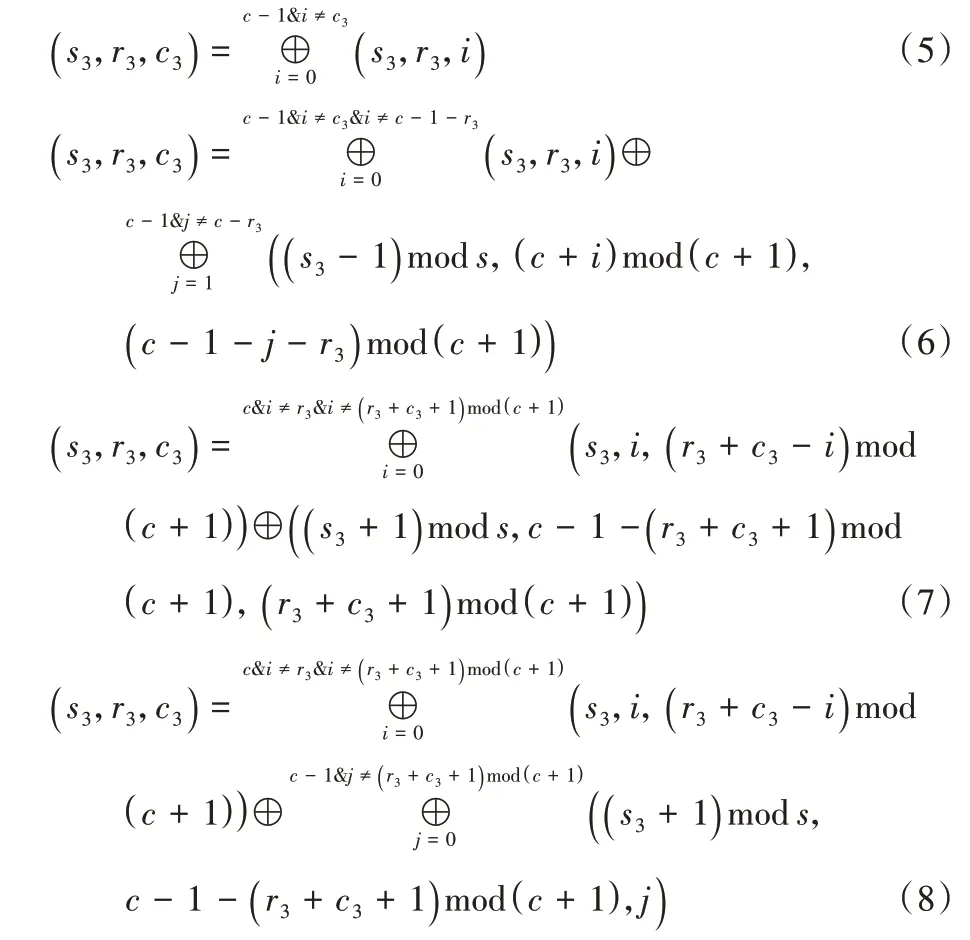

2.3.1 单条带单元失效情况下的重构

任意单条带单元(

s

，

c

)失效，(

s

，

r

，

c

)表示失效条带单元上的失效块。重构条带单元(

s

，

c

)时，需要读取条带单元组

s

和(

s

+1) mod

s

中块。例如，Code-LM（3，4）中条带单元（1，1）失效，恢复（1，1）时，需要读取条带单元组1 和2 中块，如图3 所示。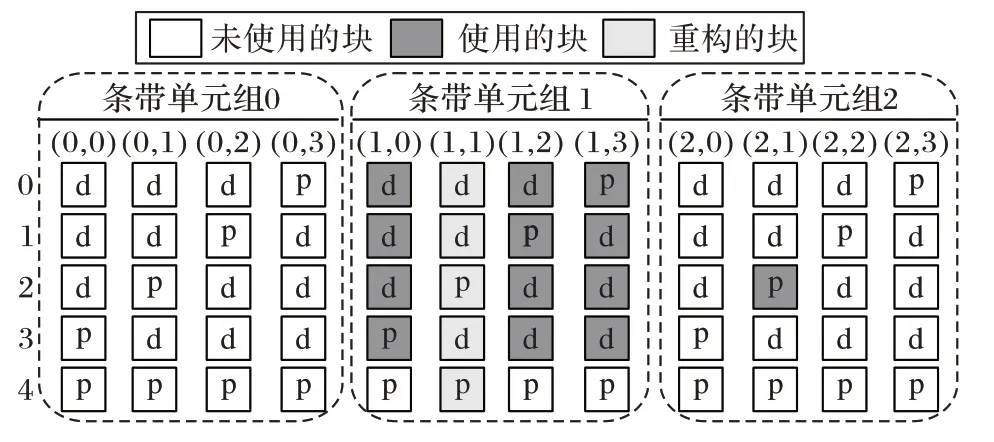

图3 单个条带单元失效，Code-LM（3，4）的重构情况Fig.3 Reconstruction with single-strip-failure in Code-LM（3，4）

重构方法如下：使用式（5）和式（1）分别恢复条带单元(

s

，

c

)上的数据块与组内水平校验块时，只需读取条带单元组

s

中行

r

上的数据；使用式（4）恢复条带单元(

s

，

c

)上的水平对角校验块时，只需额外读取条带单元组(

s

+1) mod

s

中一个水平校验块，原因在于失效水平对角校验块所在重构链与其他失效块所在重构链有且只有一个交点。算法1 描述了此情况下，Code-LM（

s

，

c

）的重构过程。算法1 基于Code-LM（

s

，

c

）的RAID 组中任意失效条带单元(

s

，

c

)重构算法。步骤1 标识失效条带单元(

s

，

c

)。

步骤2 重构失效条带单元：

使用条带单元组

s

中同一行的块重构失效块。

2.3.2 双条带单元失效情况下的重构

任意两个条带单元(

s

，

c

)、(

s

，

c

)失效时，分为以下3 种情况：1）条带单元(

s

，

c

)、(

s

，

c

)在同一条带单元组，即

s

=

s

，

c

≠

c

；2）条带单元(

s

，

c

)、(

s

，

c

)在距离为1 的两个条带单元组，即(

s

+1) mod

s

=

s

；3）条带单元(

s

，

c

)、(

s

，

c

)在距离大于1 的两个条带单元组（此时条带单元组的数目不小于4）。

下面根据不同故障情况给出对应的重构算法。

1）条带单元(

s

，

c

)、(

s

，

c

)在同一条带单元组。若存在一条校验链，该校验链与失效条带单元有且仅有一个交点，即该校验链中有且仅有一个块失效，那么该失效块可恢复，并且为恢复序列的起点。由Code-LM（

s

，

c

）的结构可知，存在

c

条水平对角校验链，它们的对角数据块位于条带单元组

s

，水平数据块位于条带单元组(

s

+1)mod s，由于每一个条带单元中数据块的数目为

c

-1，因此这

c

条水平对角校验链中必存在一条校验链的水平数据块部分与失效条带单元(

s

，

c

)没有交点。同理可得，必然存在另外一条水平对角校验链的水平数据块部分与失效条带单元()

s

，

c

没有交点。综上所述，这两条水平对角校验链中的失效数据块可作为恢复序列的起点。重构失效条带单元(

s

，

c

)、(

s

，

c

)时，需要读取条带单元组(

s

-1) mod

s

、(

s

+1) mod

s

和

s

中的数据。Code-LM（3，4）中条带单元（1，1）、（1，2）失效，重构需要读取条带单元组0、1和2中的块。重构块之间的箭头表示重构顺序关系，即只有恢复箭头起点的块后，才可以恢复箭头终点的块，如图4所示。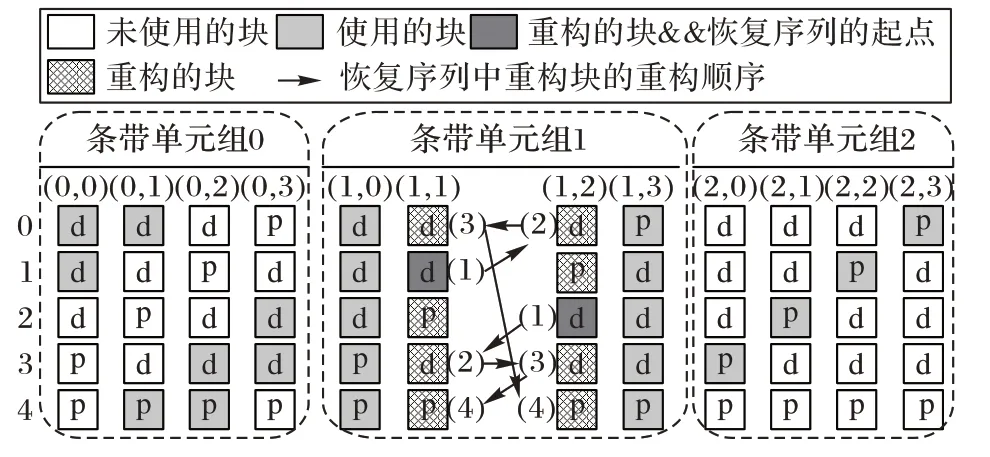

图4 两个条带单元失效且在同一条带单元组，Code-LM（3，4）的重构情况Fig.4 Reconstruction with double-strip-failure in one strip-set in Code-LM（3，4）

重构方法如下：重构失效条带单元(

s

，

c

)、(

s

，

c

)，首先使用式（6）重构恢复序列起点(

s

，

c

-1 -

c

，

c

)和(

s

，

c

-1 -

c

，

c

)。若未恢复数据块与已恢复块处于同一对角线，使用式（7）重构，若未恢复数据块与已恢复块处于同一行，使用式（5）重构；若失效块为水平对角校验块，使用式（4）重构。算法2 描述了此情况下，Code-LM（

s

，

c

）的重构过程。算法2 基于Code-LM（

s

，

c

）的RAID 组中，同一条带单元组中任意两个失效条带单元(

s

，

c

)、(

s

，

c

)的重构算法。步骤1 标识失效的两个条带单元(

s

，

c

)、(

s

，

c

)。

步骤2 重构失效块：

步骤2.1 分别使用恢复序列起点所在的水平对角校验链上的块来重构恢复序列起点(

s

，

c

-1 -

c

，

c

)、(

s

，

c

-1 -

c

，

c

)。

步骤2.2 重构恢复序列中剩余的失效块：

以下两个重构过程同时进行：

CASE 恢复序列的起点是(

s

，

c

-1 -

c

，

c

)

2）两个失效的条带单元(

s

，

c

)、(

s

，

c

)在距离为1 的两个条带单元组，即(

s

+1) mod

s

=

s

。重构任意失效条带单元(

s

，

c

)、(

s

，

c

)时，需要读取条带单元组

s

、

s

和(

s

+1) mod

s

中块。Code-LM（3，4）中条带单元（1，2）、（2，1）失效，重构时需要读取条带单元组0、1 和2 中的块，如图5所示。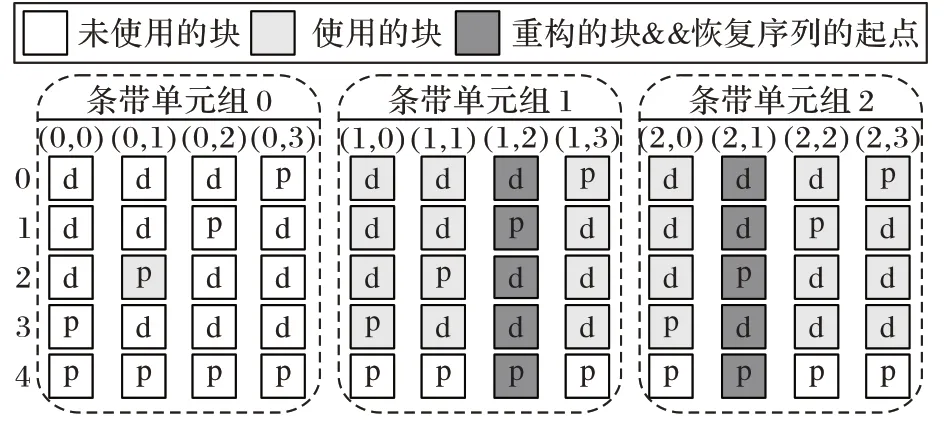

图5 两个条带单元失效且在距离为1的2个条带单元组时，Code-LM（3，4）重构情况Fig.5 Reconstruction with double-strip-failure in two adjoining strip-sets in Code-LM（3，4）

重构方法如下：若失效块为数据块或组内水平校验块，使用式（5）重构；若失效块为水平对角校验块，使用式（4）重构。算法3 描述了此情况下，Code-LM（

s

，

c

）的重构过程。算法3 基于Code-LM（

s

，

c

）的RAID 组中任意两个失效条带单元(

s

，

c

)、(

s

，

c

)的重构算法，(

s

+1) mod

s

=

s

。步骤1 标识失效条带单元(

s

，

c

)和(

s

，

c

)。步骤2 重构条带单元(

s

，

c

)的失效块：

使用条带单元组

s

上同一对角线的块和条带单元组(

s

+

使用条带单元组

s

上同一行的数据块重构失效块。3）两个失效条带单元(

s

，

c

)、(

s

，

c

)在距离大于1 的两个条带单元组。Code-LM（

s

，

c

）重构任意失效条带单元(

s

，

c

)和(

s

，

c

)时，需要读取条带单元组

s

、

s

、(

s

+1) mod

s

和(

s

+1) mod

s

中块。Code-LM（4，4）中条带单元（1，1）和（3，1）失效，重构需要读取条带单元组0、1、2 和3 中的块，如图6 所示。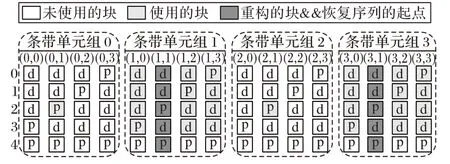

图6 两个条带单元失效且在距离大于1的2个条带单元组时，Code-LM（4，4）重构情况Fig.6 Reconstruction with double-strip-failure in two different strip-sets with strip-set distance of 1 in Code-LM（4，4）

重构方法如下：若失效块为数据块或组内水平校验块，使用式（5）重构，若失效块为水平对角校验块，使用式（4）重构。算法4 描述了此情况下，Code-LM（

s

，

c

）的重构过程。算法4 基于Code-LM（

s

，

c

）的RAID 组中任意两个失效条带单元(

s

，

c

)、(

s

，

c

)重构算法（且两个条带单元在距离大于1 的条带单元组）。步骤1 标识失效条带单元(

s

，

c

)和(

s

，

c

)。步骤2 重构条带单元(

s

，

c

)的失效块：

3 Code-LM（s，c）性能分析

本章对Code-LM（

s

，

c

）的编码效率、存储效率、读写性能、重构开销与重构性能进行分析，并将其与RDP-Code（

n

-2，

n

）、Code-M(

s

，

c

)、V-Code(

m

，

n

)作比较。基于不同编码的每个RAID 分组中磁盘的总数目均为

n

，

n

=

s

×

c

。每个磁盘完全相同，设单盘容量固定为

d

个块，每个块的大小相同。

3.1 编码效率

编码效率可定义为编码所需异或（Exclusive OR，EOR）运算次数与磁盘阵列中的数据块数量的比值，因此编码效率值越小，编码效率越优，编码计算负载越小。

当磁盘数目相同时，与RDP-Code（

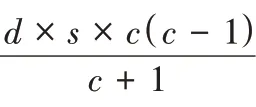
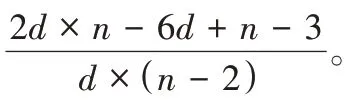
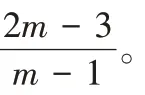
n

-2，

n

）、V-Code（

m

，

n

）相比，Code-LM（

s

，

c

）的编码效率最优，Code-LM（

s

，

c

）编码时的计算负载最小，如图7 所示。原因在于其牺牲了一定的存储空间，分布更多的校验块，生成一个校验块所需的数据块更少，缩短了校验链长度。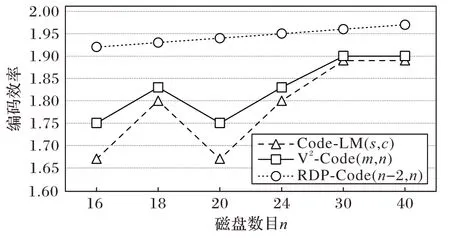

图7 编码效率对比结果Fig.7 Comparison results of coding efficiency

3.2 存储效率

存储效率可定义为磁盘阵列中数据块的数目与磁盘阵列中所有块的数目的比值。

当磁盘数目相同时，与RDP-Code（

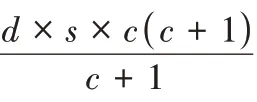
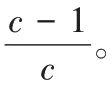
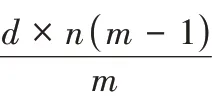
n

-2，

n

）、V-Code（

m

，

n

）和Code-M（

s

，

c

）相比，Code-LM（

s

，

c

）存储效率最低，由于其牺牲了一定的存储空间，存放更多的校验块。当

c

增加时，Code-LM（

s

，

c

）存储效率增加，且与其他编码的存储效率差距不断减小。例如，当

c

=4，6，10，12，16，18 时，对应的磁盘数目

n

=12，18，30，36，48，54，对应的存储效率分别为60%、71%、82%、85%、88%、89%，如图8 所示。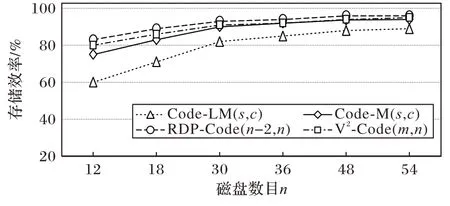

图8 磁盘数目相同时，编码存储效率比较Fig.8 Comparison of storage efficiency with same numbers of disks

3.3 无磁盘故障情况下的Code-LM（s，c）读写性能分析

无磁盘故障情况下，磁盘阵列存在读和写两种操作。读操作包括小读（一次读一个块）和条带单元读（一次读一个条带单元），写操作包括小写（一次写一个块）和条带单元写（一次写一个条带单元）。

1）读操作：由于Code-LM（

s

，

c

）是垂直编码，其校验块均匀分布在每个条带单元上，因此在无磁盘故障时，其小读操作没有引起额外的开销；由于每个条带单元都存在校验块且校验块无需读取，所以其条带单元读不能完全占有单个磁盘上的连续读带宽。2）写操作：由Code-LM（

s

，

c

）编码规则可知，任意一个数据块参与3 个校验块的生成，分别是两个水平对角校验块，一个组内水平校验块，因此在正常模式下，其小写操作会引起3 个校验块的写操作。Code-M（

s

，

c

）与V-Code（

m

，

n

）小写操作均引起2 个校验块的更新，因此与Code-M（

s

，

c

）、V-Code（

m

，

n

）相比，Code-LM（

s

，

c

）小写开销最大。由于Code-LM（

s

，

c

）中任意一个条带单元数据块的数目为

c

-1，因此其条带单元写将更新校验块的数目为3(

c

-1)，更新磁盘的数目为2(

c

-1)。由于Code-LM（

s

，

c

）中条带单元组数目至少为2，因此在存储规模相同的情况下，与水平编码相比，其条带单元写开销较大；与垂直编码相比，其条带单元写开销较小。

3.4 单盘故障时，Code-LM（s，c）重构开销

解码复杂度决定了重构效率，影响系统可靠性。

由算法1 可知，失效数据块与失效组内水平校验块所在的重构链长度为

c

，失效水平对角校验块所在的重构链长度为

c +

1；使用式（1）重构失效数据块和组内水平校验块时，需要的异或操作数均为

c

-2，使用式（4）重构失效水平对角校验块时，需要的异或操作数为

c

-1。由于任意失效条带单元中，数据块数目为

c

-1，组内水平校验块和水平对角校验块数目均为1，因此为恢复任意失效条带单元，Code-LM（

s

，

c

）需要读取的块个数为

c

×(

c

-1)+1，写入的块的个数为

c

+1，即I/O 复杂度为

c

+2，计算总复杂度为

c

-

c

-1。

3.5 双盘故障时，Code-LM（s，c）重构开销

双盘故障时分为以下3 种情况：

1）任意两个故障磁盘在同一条带单元组。

由算法2 可知，恢复序列中恢复起点所在重构链长度为2

c

-1，失效水平对角校验块所在的重构链长度为

c

，其他失效块所在重构链长度为

c

+1；恢复任意两个失效条带单元，需要读取的块数目为(

c

+1) ×(

c

-2)+3

c

，需要写入的块的数目为2(

c

+1)，I/O 复杂度为

c

+4

c

，计算总复杂度为2

c

+

c

-4。

2）任意两个故障磁盘在距离为1 的两个条带单元组。

使用算法3 重构时，失效数据块与组内水平校验块所在的重构链长度为

c

，失效水平对角校验块所在重构链长度为

c

+1；恢复任意两个失效条带单元，需要读取的块的数目为2

c

×(

c

-1)+1，需要写入的块的数目为2(

c

+1)，I/O 复杂度为2

c

+3，计算总复杂度为2(

c

-

c

-1)。

3）任意两个故障磁盘在距离大于1 的两个条带单元组。

使用算法4 重构时，失效数据块与失效组内水平校验块所在的重构链的长度为

c

，失效水平对角校验块所在的重构链长度为

c

+1，恢复任意两个失效条带单元，需要读取的块的数目为2

c

×(

c

-1)+2，需要写入的块的数目为2(

c

+1)，I/O 复杂度为2

c

+4，计算总复杂度为2(

c

-

c

-1)。

3.6 Code-LM（s，c）重构性能比较

将Code-LM（

s

，

c

）与同时具有组内水平校验块和对角校验块的RDP-Code（

n

-2，

n

），具有水平对角校验块的Code-M（

s

，

c

），具有对角校验块V-Code（

m

，

n

）进行比较。为便于比较作出如下假设：

用于数据重构的总带宽是相同，即单位时间内完成与重构相关的数据读写总量是固定的。

重构时读取数据块的个数决定了重构时间，读取数据块个数越少，重构时间越少，重构性能越好。

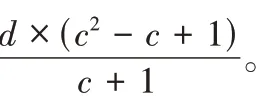
任意双盘故障分为以下3 种情况：

RDP-Code（

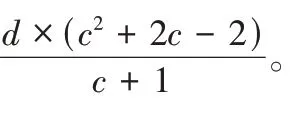
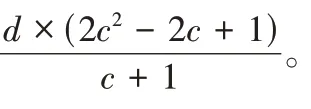
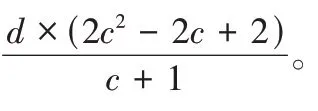
n

-2，

n

）：任意单盘故障时，失效数据块所在重构链长度为

n

-1，任意单盘重构需要读取的块个数为

d

×(

sc

-2)；双盘重构需要读取的块个数为

d

×(

sc

-2)。在磁盘数目相同时，Code-LM（

s

，

c

）的任意单盘和双盘重构性能均优于RDP-Code（

n

-2，

n

）。当

c

一定时，随着s 的增加，任意单盘和双盘重构时间比率会进一步降低。

s

=3，

c

=4，Code-LM（3，4）牺牲的存储效率为0.23，任意单盘重构时间 为RDP-Code（10，12）的0.26 倍，双盘重构时间为RDP-Code（10，12）的0.44 倍；

s

=4，

c

=4，Code-LM（4，4）牺牲的存储效率为0.28 倍，任意单盘重构时间为RDP-Code（14，16）的 0.19 倍，双盘重构时间为RDP-Code（14，16）的0.31 倍；

s

=5，

c

=6 时，与RDP-Code（

n

-2，

n

）相比，Code-LM（

s

，

c

）的单盘和双盘重构时间减少最多，Code-LM（5，6）单盘和双盘重构时间分别为RDP-Code（28，30）的0.16 倍和0.23 倍，即分别减少了84%和77%如图9 所示。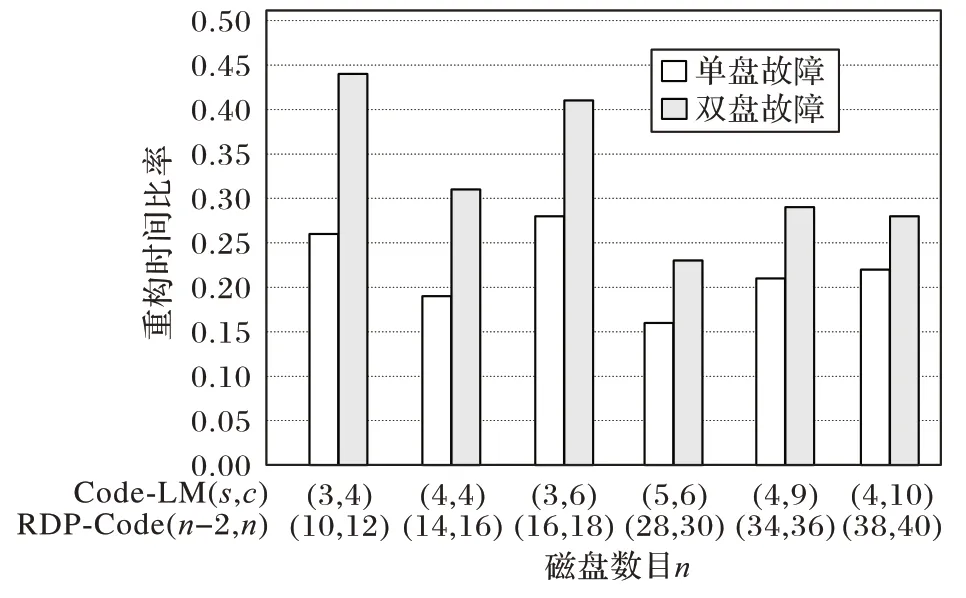

图9 Code-LM（s，c）与RDP-Code（n -2，n）重构时间比较Fig.9 Comparison of reconstruction time between Code-LM（s，c）and RDP-Code（n -2，n）

针对RDP-Code（

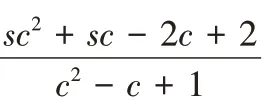
n

-2，

n

）中的任意单盘故障情况，Xiang等提出了单盘修复优化算法RDOR（Row-Diagonal Optimal Recovery），与RDP-Code（

n

-2，

n

）的传统单盘修复算法相比，其减少了单盘重构时间，提高了单盘重构性能；Code-LM（

s

，

c

）的单盘重构性能优于单盘恢复优化算法RDOR。当磁盘数

n

=12 时，Code-LM（3，4）的单盘重构时间为RDP-Code（10，12）的0.26 倍，为RDOR 的0.42 倍；当磁盘数目

n

=30 时，Code-LM（5，6）中单盘重构时间为RDP-Code（28，30）的0.16倍，为RDOR的0.23倍，如图10所示。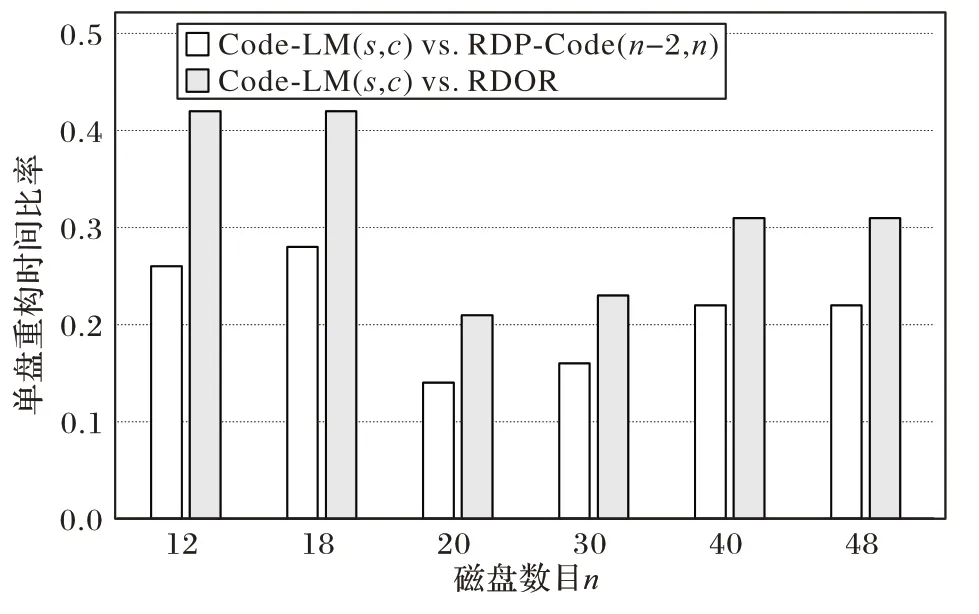

图10 Code-LM（s，c）与RDP-Code（n -2，n），RDOR单盘重构时间比较Fig.10 Comparison of reconstruction time of single disk failure between Code-LM（s，c）and RDP-Code（n -2，n），RDOR

Code-LM（

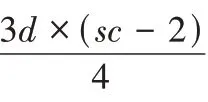
s

，

c

）的任意单盘重构性能和双盘重构性能均优于Code-M（

s

，

c

）。当

s

一定时，随着

c

增加，牺牲的存储效率进一步减小，双盘重构时间比率会进一步降低。

s

=3，

c

=4，Code-LM（3，4）牺牲的存储效率为0.15，双盘重构时间为Code-M（3，4）的0.49 倍；

s

=3，

c

=6，Code-LM（3，6）牺牲的存储效率为0.12，双盘重构时间为Code-M（3，6）的0.44 倍；

s

=3，

c

=10，Code-LM（3，10）牺牲的存储效率为0.08，双盘重构时间为Code-M（3，10）的0.40 倍，如图11 所示。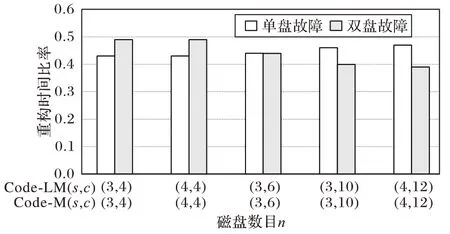

图11 Code-LM（s，c）与Code-M（s，c）重构时间比较Fig.11 Comparison of reconstruction time between Code-LM（s，c）and Code-M（s，c）

当

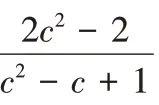
m

=

c

+1 时，随着

c

增加，Code-LM（

s

，

c

）牺牲的存储效率进一步减小，任意单盘重构性能和双盘重构性能均优于V-Code（

m

，

n

）。

s

=5，

c

=4 时，Code-LM（5，4）牺牲的存储效率 为0.2，双盘重构时间为V-Code（5，20）的0.31 倍，Code-LM（5，4）单盘重构时间为V-Code（5，20）的0.33 倍，即减少了67%；

s

=5，

c

=6，Code-LM（5，6）牺牲的存储效率为0.14，双盘重构时间为V-Code（7，30）的0.30 倍；

s

=5，

c

=10，Code-LM（5，10）牺牲的存储效率为0.09，双盘重构时间为V-Code（11，50）的0.28 倍；

s

=4，

c

=10，与V-Code（

m

，

n

）相比，Code-LM（

s

，

c

）双盘重构时间减少最多，Code-LM（4，10）的双盘重构时间为V2-Code（11，40）的0.28 倍，即Code-LM（4，10）双盘重构时间减少了72%，如图12 所示。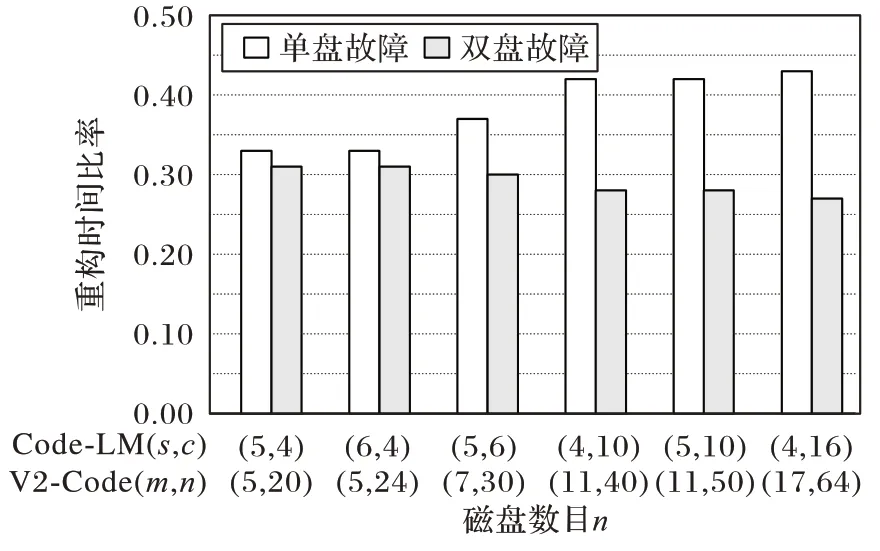

图12 Code-LM（s，c）与V2-Code（m，n）重构时间比较Fig.12 Comparison of reconstruction time between Code-LM（s，c）and V2-Code（m，n）

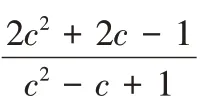
4 结语

本文提出了一种支持故障磁盘快速恢复，可容忍任意双盘失效和其他形式多盘失效的新型Non-MDS 编码：Code-LM（

s

，

c

）。Code-LM（

s

，

c

）是垂直编码，校验块在每个条带单元中均匀分布。它根据不同的故障情况采用不同的恢复方法，它与通用的MDS 编码相比，分布了更多的校验块，缩短了重构链的长度，缩短了重构时间，提高了重构性能，重构性能稳定且与存储系统规模无关。理论分析和实验结果表明，Code-LM（

s

，

c

）可提高大规模存储系统中数据可靠性。在未来的工作中，为了进一步提高存储系统的可靠性和容错性，将研究一种新型Non-MDS 编码，该编码可容任意多盘故障。