深度强化学习解决动态旅行商问题

陈浩杰，范江亭，刘 勇

（黑龙江大学计算机科学与技术学院，哈尔滨 150006）

0 引言

生活中的运输路线的设计、配送快递等旅行商问题往往会涉及选择动作的过程，即节点序列顺序的预测问题，例如对于运输路线的设计决定以什么顺序设计运输路线，快递配送问题是决定在下一个时间选择哪个客户节点作为配送点等，这些决策问题都属于组合优化问题中的旅行商问题，并且很多情况下属于NP-hard 问题，加入动态网络信息后，问题所映射到图的规模非常大，解决这些问题的资源消耗随着图的节点增多呈指数倍数增长，所以有必要针对这些问题研究出更加贴合实际的求解方法。

近些年，利用强化学习自动学习不断变化的节点信息的算法成为机器学习的一大新的探索，本文提出一个结合变体Transformer机制和分布式强化学习的统一模型Dy4TSP（Dynamic model for Traveling Salesman Problems），来求解动态旅行商问题中涉及到图的动态节点的情况。为了更高效地处理动态图信息，在输出节点序列时，使用Transformer 的变体通过某种方式得到与每个输入序列相关联的权值，用此权值来指导模型输出。整个模型只需要输入动态图信息，选择要处理的旅行商问题类型，就可以预测出对应问题的几种最优决策的节点解序列。不同于以往贪心产生唯一解的方式，该模型会预测出多个拥有最优奖励值的路线，减少漏掉整条条件概率最大的路线的可能性；并且与大多数经典启发式不同，当输入图的节点或者边信息和训练时的变化不同时，模型依旧保持鲁棒性。为解决图规模的动态组合优化问题，特别是那些难以设计启发式的旅行商问题提供了新的方向。

本文的主要工作如下：

1）提出一个将多头注意力机制与分层强化学习结合来求解动态图上的旅行商问题的轻量级模型Dy4TSP；

2）本文模型加入了节点动态变化的元素，随着配送车辆对节点的遍历，车辆剩余负载和客户节点的需求量发生变化，更加接近于实际生活中的旅行商问题；

3）本文模型采用分布式强化学习算法融合参数量更少的图卷积神经网络网络和预测网络部分，并行地训练模型，所需的训练时间更少，在更短的时间内获得更好的训练效果；

4）本文模型是可扩展的，针对不同的维度都可以选择相应的旅行商问题并输入到模型中进行预测与训练，为不同维度的旅行商问题提供了统一的模型。

本文模型可以在没有标签的情况下，经过分布式强化学习算法的训练为动态旅行商问题的学习提供比以往模型准确率更高的方法。

1 相关工作

最近人们对用深度学习和强化学习来解决图的组合优化问题产生了兴趣。最初将深度强化学习用于组合优化问题是Vinyals 等引入了指针网络（Point Network，PN），对输入序列按照注意力机制得到的概率值重新排列作为模型的输出，缺陷是该模型基于有监督学习，严重依赖于标签数据。

Bello 等第一次尝试用强化学习算法解决组合优化问题，解决了强化学习需要标签的问题，但模型的设计过程没有针对处理图结构的输入问题，没有得到很好的扩展应用。

Sutskever 等通过将图变换为一个序列，然后再基于序列到序列模型来生成节点决策顺序。这种方法存在的问题非常明显，在将图变换为序列的过程中会丢失大量的结构信息。

Khalil 等使用基于图网络表征的单一模型，通过拟合Q-learning训练模型输出节点插入到局部路线中的顺序，每一步为智能体提供增量奖励有效地学习贪心算法来依次构造最优解。缺点是模型需要人为的设计辅助函数，泛化能力差。

Kulkarni 等介绍了一个分层强化学习模型，这是强化学习领域最经典的并行分布式工作，可以结合不同层次的动作价值函数，多个时间尺度的抽象来帮助智能体的优化策略，为本模型的训练模型的分布式学习提供了新的思路。

Nazari 等将指针网络的编码器替换为一维卷积层直接进行节点序列的表征过程，从而可以有效更新状态变化后节点表征向量，他们将该模型应用于车辆路径问题中，减少了很多动态节点变化上的不必要的计算。

Gao 等利用图注意力神经网络以及循环神经网络对组合优化问题的排序策略进行学习，采用PPO（Proximal Policy Optimization）强化学习算法对模型进行训练，但是在优化能力上未达到或极度靠近最优解。

本文不同于以上模型，本文结合多头注意力机制和分布式强化学习方法，以一种自动学习的方式，实时地生成问题的解，不但拥有高效的收敛性，而且得到的结果更加接近最优解。

2 问题定义

经典旅行商问题（Traveling Salesman Problem，TSP）：配送车辆从图中配送中心节点出发，经过所有城市一次且仅一次并回到配送中心，目标是配送客户节点需求数多，且配送路径最短。

配送收集旅行商问题（Distribution Collection Traveling Salesman Problem，DCTSP）：配送车辆从图中配送中心节点出发，由一限定负载容量的配送车辆负责配送需求大于零的客户，目标是配送客户节点需求数多，且配送路径最短。

拆分交付旅行商问题（Split Delivery Traveling Salesman Problem，SDTSP）：在配送收集旅行商问题的基础上，将每个客户的需求量拆分成多部分，允许配送车辆对客户节点的需求量大于车辆剩余负载的客户节点进行配送，该解决方案可以将给定客户节点的需求量分配到多条路线以减少空载率。

3 神经网络构建

将对动态旅行商问题求取最优解的过程看成序列决策问题，整体用马尔可夫决策过程建模，通过设计一个最优策略的概率分布函数，来达到建立实时输出可行解序列的参数化模型的目标，模型的训练通过分布式强化学习训练产生近似最优解来修正预测模型输出的节点序列顺序。

神经网络构建阶段包括网络模型创建和模型训练两阶段，主要分为3 个步骤，如图1 所示。

1）Graph2Vec 图卷积神经网络，以整个

T

时刻的图

G

和到目前为止输出的节点集

S

依次作为输入，由前馈网络结合邻居及节点信息进行聚合操作，输出某个时刻每个节点的向量序列，如图1（a）所示；2）Vec2Seq 预测网络，将Graph2Vec 网络的输出中取

t

时刻预测网络未输出节点的表征向量，连接上一时刻预测网络已输出的节点，依次输入到多头上下文注意力机制和Softmax 层，得到

t

时刻节点的概率分布，依据概率分布等信息输出前

b

个节点作为Vec2Seq 预测网络预测得到的

t

+1时刻将要遍历的节点，如图1（b）所示，第1）～2）部分作为本文的主体模型进行实时输出可行解序列的工作；3）n2Drl 训练网络，对以上创建的网络模型进行训练，将Graph2Vec 网络的节点表征向量与Vec2Seq 网络的预测节点部分输入到

n

个线程的Actor 中，多个线程分布式探索环境，积累状态过度量（状态，动作，奖励）等信息，一个批次结束后更新状态过渡向量的优先级并存入经验缓存机制中，使用多个线程并行运行的方式更加高效地收集大规模图数据，如图1（c）所示。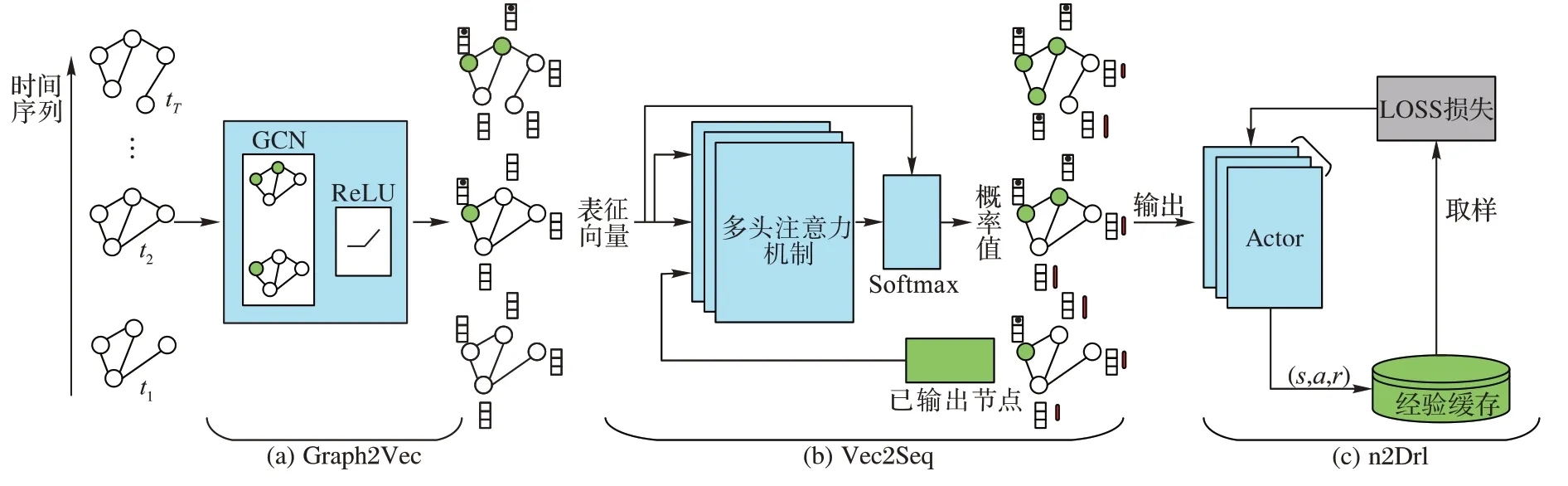

图1 神经网络构建框架Fig.1 Neural network construction framework

综上，通过Graph2Vec 生成网络表征，将每个时刻的节点表征向量提供给Vec2Seq 预测网络进行节点序列预测，与此同时Vec2Seq 预测网络同步更新网络参数，使得对于图中的每个节点，可以更准确地判断出该节点是否是最优解的一部分。

3.1 Graph2Vec图卷积网络

Trivedi 等使用了循环神经网络（Recurrent Neural Network，RNN）框架，使得某一时刻的节点计算依赖于上一时刻的计算结果，很难具备高效的并行计算能力，并且RNN 的网络结构对于长距离和层级化的依赖关系难以建立，尤其是在本文所研究的动态旅行商问题中，这样导致求解问题随着输入顺序动态改变，网络预测的性能有一定的差异。同时在时间序列中对图神经网络截取快照是一种粗糙的方法，基于此Graph2Vec 网络使用连续时间的节点表征，通过聚合邻居节点的信息，直接在图中进行卷积操作，产生整个时间序列的向量作为节点表示。

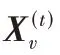
3.2 Vec2Seq预测网络

在这部分网络中，延用了NLP（Natural Language Processing）中广为应用的成熟技术Transformer 模型，由于Transformer 使用自注意力机制和前馈神经网络等结构搭建网络，解决了RNN 模型的长期依赖问题，并且相对于卷积神经网络可以更好地进行并行计算，可以有效地处理动态网络结构，所以Vec2Seq 预测网络仅基于多头上下文注意力机制从多个角度计算Graph2Vec 的节点表征序列对预测模型输出序列的注意力权重，来指示当前输出的节点，提高了整个模型的预测准确度。

最后Vec2Seq 预测网络通过Softmax 传递结果，如式（6）利用Softmax 函数使所有未输出节点的相似性量归一化，把相似性

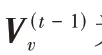
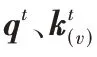
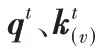
C

映射成0 到1 之间的实数，将此数值作为节点

u

和邻居节点

v

的概率值，此后在预测节点时可以选取相应概率的节点作为Vec2Seq 预测网络的目标输出。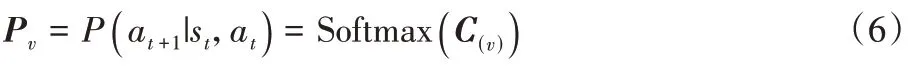

输出节点前首先判断目标节点的需求值是否大于0，满足条件后开始进行节点序列输出，输出的过程中使用集束搜索算法取代贪心算法，每次深度扩展解时只保留概率值最大的前

b

个节点加入集合

S

，其中

S

表示属于已输出的节点集。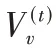

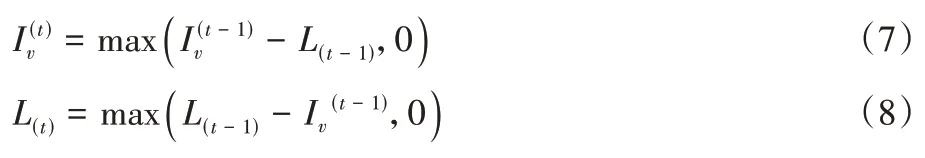
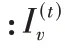
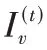
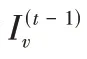
3.3 n2Drl训练网络

本文考虑使用一种自我驱动性的深度强化学习算法n2Drl 来训练模型，该算法的理论模型基于马尔可夫决策过程，该理论让智能体在所给的环境状态中通过奖励值的反馈自主学习做动作，以使累积奖励最大化。由于动态旅行商问题中模型需要训练的样本的数量相较于之前会有成倍数增长的趋势，在这种情况下，引入分布式强化学习，采用并行智能体策略，把任务分配到不同的智能体上，复制

n

个线程，在每个线程运行一个智能体同所给的环境进行交互来并行缩短收集数据的时间。在第二部分Vec2Seq 预测网络输出可行解序列后，训练过程中需要计算出输出这

b

个节点后所带来的奖励值，通过奖励值来衡量当前节点动作的优劣，更新函数如式（9）：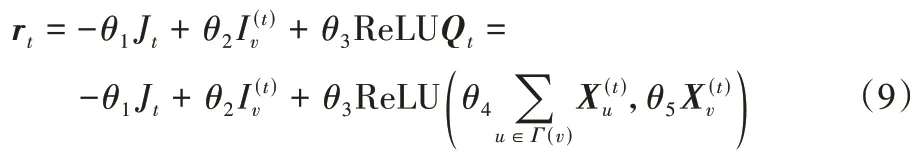

其中：

Q

表示

t

时刻状态行为值函数，表示配送车辆在策略

P

(

a

|

s

，

a

)和当前状态

s

下，采取动作

a

作为解的优劣程度，如式（9）所示为当前输出的节点

v

和其所有邻居节点的拼接，

J

表示

t

时刻的路径长度，为遍历前后客户节点的二维坐标位置

F

的平方差，其中

θ

是每一个部分的权重参数，决定了每个部分对动作奖励值的贡献度。本文将截止到

t

时刻为止智能体探索环境所反馈回的总奖励值定义为

R

，如式（10）所示，计算多步奖励的过程中引入衰减因子

γ

，作为下一时刻奖励值的系数，令未来状态所反馈回的奖励值以不同程度的衰减度递归地指导智能体做决策，来同时关注决策后的眼前利益和未来奖励。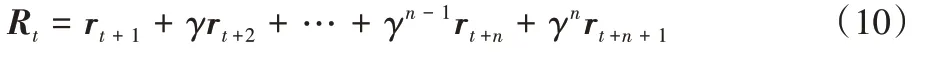

之后将这些数据，压入缓存中并随机抽取批量数据利用式（11）对带有模型参数的损失函数

L

(

W

)进行训练，训练模型的网络参数

W

由Xavier初始化器初始化，来保持各层梯度的比例大致相同，后期使用Adam优化器对损失函数式（11）进行随机梯度下降优化更新参数

W

，使得总奖励值

R

与模型输出的

t

时刻状态行为值函数

Q

越来越接近，并将优化后的网络参数

W

进行输出作为n2Drl 训练网络的训练结果。

4 实验与结果分析

4.1 Vec2Seq预测网络参数设置

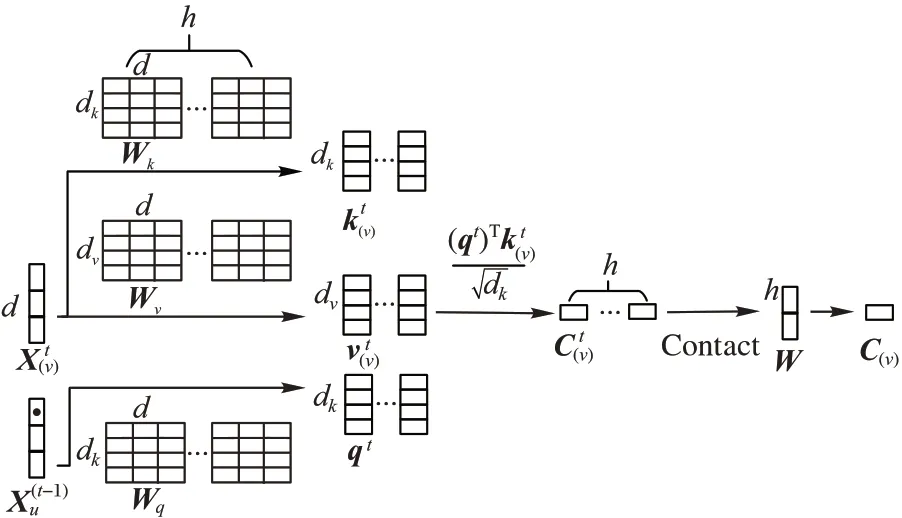
图2 多头注意力机制Fig.2 Multi-head attention mechanism

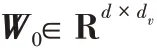
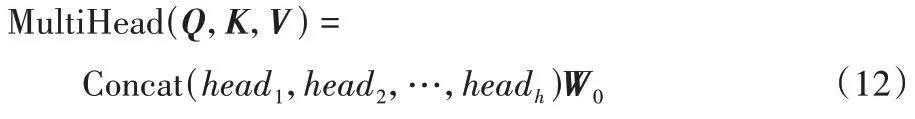
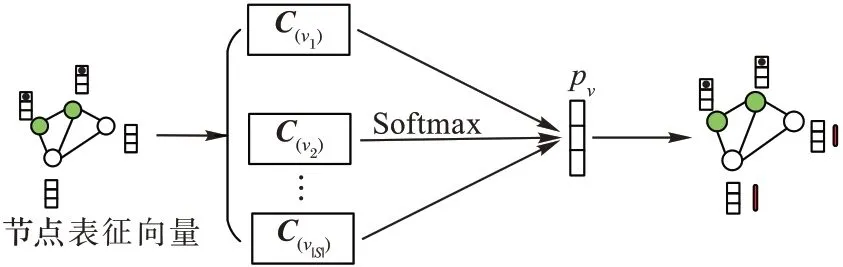
图3 Softmax函数网络结构Fig.3 Softmax function network structure

4.2 实验参数设置

对于任意时刻

t

(

t

=0，1，…，

T

(

T

≥0))，考虑到现实中旅行商问题的节点分布随机性，本文随机生成有着不同需求量的客户节点来模拟现实世界，实验过程中随机生成1 000 个图，图中客户节点数目设置皆为20、50 和100 个，将这些图

G

(

V

，

E

)输入到本文的模型Dy4TSP 中。本文对所提出的模型进行实验，设置每个epoch 处理256 个批次，迭代次数皆为30 次，设置时间最大为

T

=100，在训练模型的过程中，学习率设为0.000 1，从Replay Memory 中采样的训练样例为16，训练模型的网络参数

W

使用Adam优化器对损失函数式（11）进行随机梯度下降来更新，其中梯度下降的参数设置

β

=0.9，

β

=0.99，

ε

=10。与此同时，发现本文模型在配送收集旅行商问题、拆分交付旅行商问题的图训练时的超参数和旅行商问题的超参数一致，这样可以在不同的问题上节省调整参数的时间。为了减少训练时间，使得模型更快地收敛到预计的效果，加入预训练过程，使用已训练好的模型训练新的网络，由经过预训练的模型来解决不同节点数目的同类型旅行商问题，本文模型（

T

≥0）比没有在相同实例大小问题上训练表现好，这表明本文加入预训练过程的模型可以很好地泛化到不同节点的实例问题中。

4.3 对比实验

由于旅行商问题亦属于组合优化问题，所以针对所研究的旅行商系列问题，本文将选取处理组合优化问题的模型PN、S2V（Structure2Vector）、注意力模型（Attention Model，AM）、带有边嵌入的图注意网络（Graph Attention Network with Edge Embedding，EGATE）和动态强化学习网络（Dynamic Reinforcement Learning network，DyRL）与本文模型Dy4TSP 作对比，以启发式算法优化器LKH3（Lin-Kernighan-Helsgaun3）得到的路径长度为最优性能基准。图4（a）、（b）展示了在固定客户节点数目的TSP、DCTSP 上使用不同的模型，所得到的和开源求解器LKH3 的最优性能差距，即最优路径的差距对比，图4（c）表示不同的模型对于不同节点数的SDTSP 问题的最优路径长度。图4（a）、（b）中的TSP100 表示该旅行商问题由100 个客户组成，对于TSP100而言，本文模型在最优路径上的优化性能超越了其他对比模型大约0.15 到0.37 个单位，比较接近于EGATE 模型，并且在20 个节点时可以达到LKH3 的最优路径长度。

图4（b）加入动态元素后所有的对比模型皆与最优路径差距较大，与此同时本文模型也可以取得比对比算法较优的结果，尤其是Dy4TSP.b5 时，本文模型使用集束搜索宽度5，所有情况下，不同的节点数目皆可以达到0.1 到1.05 的最优路径差距；由于SDTSP 没有网络上的算法求解器，本文将图4（c）的纵坐标设置为最优路径长度，将DyRL AM 模型和EGATE 模型应用于此问题，不同的模型之间有着0.01 到1.01 的差距，Dy4TSP 以不到0.1 的差距优于EGATE。基于图4 实验结果，可以发现本文模型能够比对比模型获得更优的结果，在节点数目规模达到100 个后，本文模型在不同的问题上皆明显优于对比模型，在限制时间内输出最接近最优解决方案的路线。

同时还对比了不同搜索算法对于选择节点后生成总遍历长度的影响，在测试过程中选取贪心算法和不同集束参数的集束搜索算法。理论上取样数目越多，则更容易得到理想的节点路线，然而考虑到时间复杂度会随着选取节点数目的增多成指数增长这一弊端，如何找到一个理想的临界值是加入搜索算法对比实验的目标。图4 比较了本文模型在不同搜索算法下与当前最优的开源求解器LKH3 的距离差距，其中gr 表示贪心算法，s 表示随机取样，b 表示集束搜索算法，右侧的数字表示集束宽度参数。本文发现，在使用贪心算法时的最优路径差距普遍比集束搜索算法要更长，集束宽度为5 时达到最优路径差距。

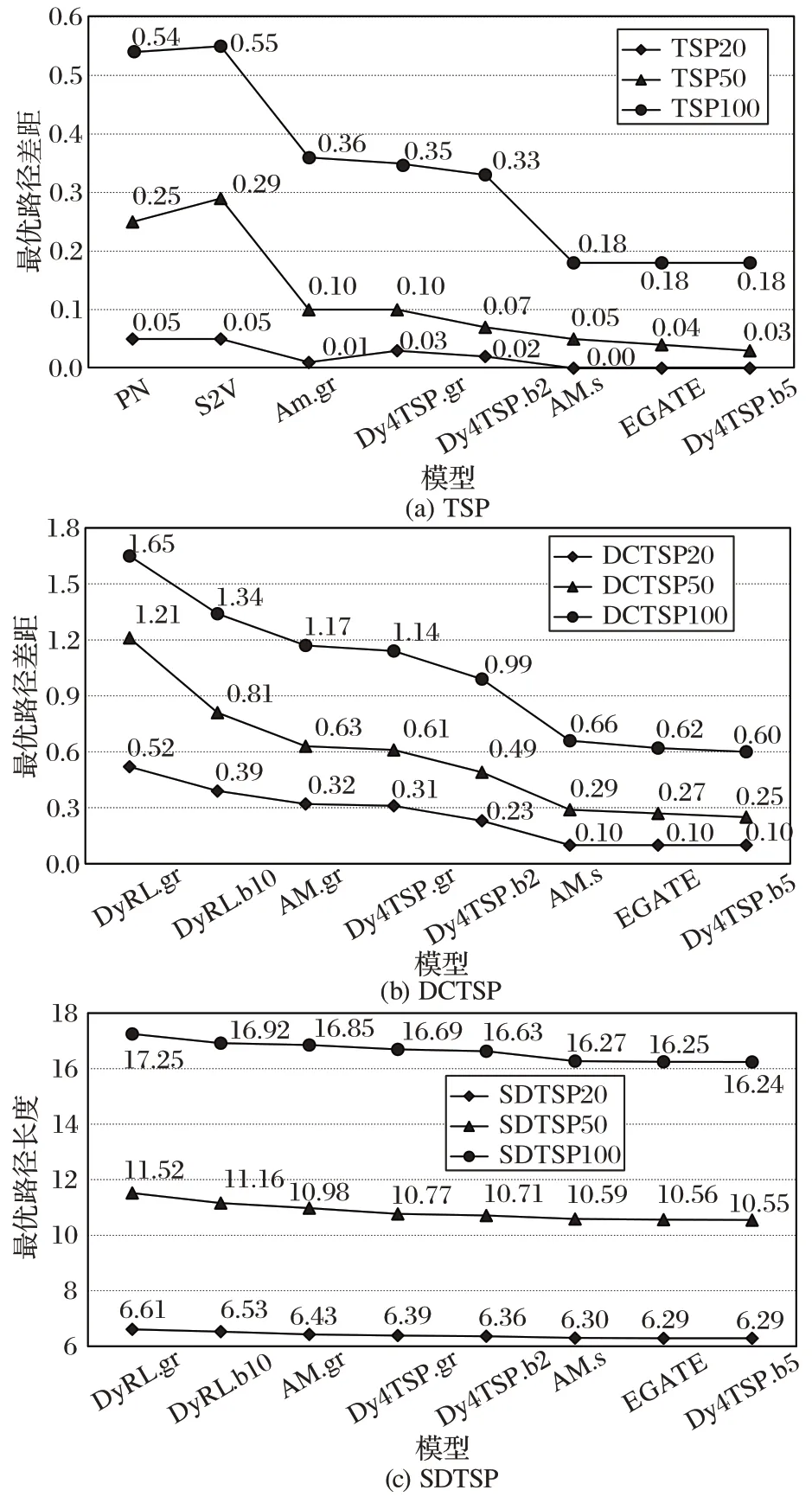
图4 不同模型的最优路径差距和最优路径长度比较Fig.4 Comparison of optimal path gap and optimal path length between different models

图5 比较了不同节点数目的SDTSP 在训练过程中随着epoch 的增加，学习网络的损失值的变化。由于学习网络随着训练时间的增多，经过反向传播、梯度优化等过程对本模型进行学习优化以及学习过程中权重矩阵的调整后，控制学习网络整体的学习幅度朝着预测更加准确的方向进行，模型的损失值在开始时快速下降，最后损失值趋于平稳，在一定范围内震荡，所以损失值后期呈现逐渐收敛于0 的状态。

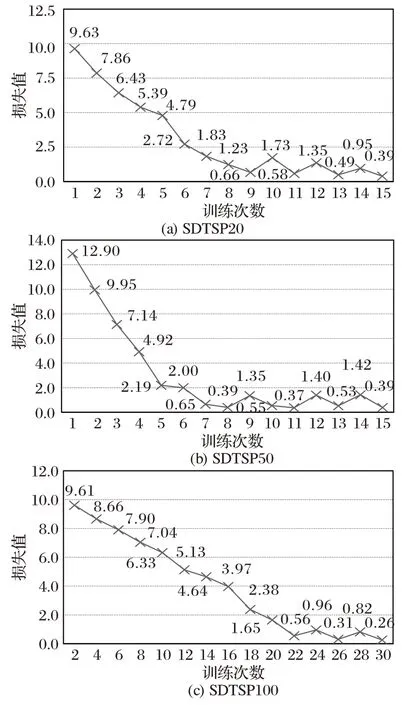
图5 不同节点数目训练损失值比较Fig.5 Comparision of training loss values for different numbers of nodes

5 结语

本文提出了一种基于强化学习模型Dy4TSP 来计算NPhard 问题中的动态旅行商问题。本文模型结合了深度学习技术和分布式强化学习方法从而得到了一种可以自动学习预测节点序列的模型。核心部分是一个Vec2Seq 预测网络，通过后期n2Drl 分布式训练网络的训练实时地生成解决方案，可以精准地预测组合优化问题中涉及序列决策问题中节点序列预测的概率，多头上下文注意力机制网络的设计和分布式强化学习训练的目的是尽可能从多个特征角度探索环境，也在尽可能少的时间合成多种解决方案，从而可以通过集束搜索算法对解决空间进行快速探索，通过大量不同节点数目的实验结果表明，Dy4TSP 显著地比现有文献中解决动态旅行商问题的技术速度更快、质量更高，可以很好地处理动态旅行商问题。