基于趋化校正的哈里斯鹰优化算法

朱 诚，潘旭华，张 勇

（天津商业大学信息工程学院，天津 300134）

0 引言

群智能优化算法是一种模拟自然界中进化机制、行为模式、物理规律，并建立特定数学模型的元启发式算法，被广泛应用于模式识别、人工智能、系统控制、信号处理等领域。大量学者在受到不同生物行为和物理现象的启发后，先后提出多种群智能优化算法，Rashedi 等提出基于万有引力定律和牛顿第二定律，通过种群的粒子位置移动来寻找最优解的引力搜索算法（Gravitational Search Algorithm，GSA）；源于对鸟群捕食的行为，通过群体中个体之间的协作和信息共享来寻找最优解，Kennedy 等提出粒子群优化（Particle Swarm Optimization，PSO）算法；Passino受大肠杆菌的群体觅食行为所启发而提出细菌觅食优化（Bacterial Foraging Optimization，BFO）算法；Mirjalili 等通过模仿鲸鱼围捕猎物时的行为方式，提出鲸优化算法（Whale Optimization Algorithm，WOA）；Dorigo 等受自然界中蚂蚁觅食的群体行为启发而提出蚁群（Ant Colony Optimization，ACO）算法。

哈里斯鹰优化（Harris Hawks Optimization，HHO）算法是Heidari 等于2019 年提出的一种新型群智能算法，该算法源于哈里斯鹰（又名栗翅鹰）捕食时的群体协作行为。整个寻优过程包括探索、探索与开发转换和开发三个阶段，具有原理简单、控制参数少、全局搜索能力出色等特点；但也存在收敛速度慢、寻优精度低、易陷入局部最优等缺点。为了克服上述缺点，学者们提出了不同的优化方法，汤安迪等通过引入Tent 混沌映射和精英等级制度策略提升算法收敛速度和精度（Chaos Elite HHO，CEHHO）；赵世杰等提出猎物能量的周期性递减调控机制，并与牛顿局部增强策略相融合实现改进HHO（Improved HHO，IHHO）；Qu 等利用信息交换机制和非线性逃逸能量因子提高种群的多样性和算法性能；Zhang 等通过对仿真实验结果进行评估，从6 种不同的能量更新策略中选出指数递减策略作为优化方案；马一鸣等对基于最大似然估计的适应度函数进行改进，有效解决针对室内到达时差定位的非线性方程求解问题；Turabieh等通过控制种群分布来改进HHO 算法，并用于预测学生潜力；Ismael 等使用基于对立学习的HHO 算法（HHO Algorithm based on Opposition-Based Learning，HHOA-OBL）用于超参数估计和特征选择；Elsayed 等将HHO 与序列二次规划相结合方法HHO-SQP（hybrid HHO with Sequential Quadratic Programming），实现电源的定向过流继电器的优化协调；刘小龙等通过多子群方形邻域拓扑结构和固定置换概率来平衡算法的探索、开发；郭雨鑫等利用精英反向学习机制和黄金正弦算法提高种群多样性并减少算法收敛时间；Guo 等利用佳点集和非线性收敛方程对HHO 进行改进；Gupta 等通过引入优化的快速俯冲策略和对立学习机制提出了HHO 的改进优化算法m-HHO（modified HHO）。

本文针对HHO 算法存在的问题提出了一种基于趋化校正的哈里斯鹰优化（Chemotaxis Correction HHO，CC-HHO）算法，从5 个方面进行改进：通过识别收敛曲线的状态，预测寻优的发展方向；引入基于生物能量消耗的逃逸能量因子

E

与跳跃距离

J

，使算法更符合生物的规律特性、更好地平衡算法的探索与开发；通过精英选择拓展算法全局搜索的广泛性；引入CC 机制提高局部搜索的精确性；当寻优陷入停滞时，对种群的逃逸能量施加扰动，强制进入探索阶段，帮助算法跳出局部最优。

1 HHO算法的介绍

HHO 算法作为一种元启发式算法，其灵感来自于哈里斯鹰的捕食过程。本章对其基本原理和数学模型进行简要说明。

1.1 探索阶段

哈里斯鹰是一种群体捕食动物，所有成员分工合作、协调行动。探索阶段是一个全局搜索的过程，鹰从空中跟踪和探测猎物。当确定目标猎物后，所有成员逐步向猎物位置靠近，围绕猎物寻找合适的位置。完成包围，为最后的攻击做准备。

所有哈里斯鹰在初始状态下随机出现在搜索空间的某一个位置，并根据两种策略向最优解移动。令

q

为位于（0，1）的随机数，当

q

＜0.5 时，每只鹰会根据种群其他成员和猎物的位置进行移动；当

q

≥0.5 时，哈里斯鹰会随机栖息在种群活动范围内的某一棵树上，其数学公式如下：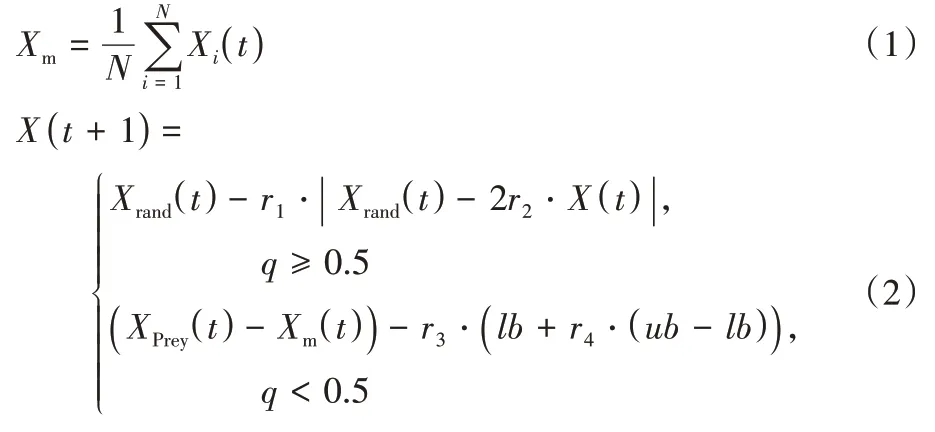

其中：

N

为种群规模；

X

为种群的平均位置；

X

（

t

+1）和

X

（

t

）分别表示第

t

+1 次和第

t

次迭代后种群所处的位置；

X

为种群中随机选择的搜索代理的位置；

X

为最优个体的位置；

r

、

r

、

r

、

r

均为（0，1）的随机数；

ub

和

lb

分别为种群的上下界。

1.2 探索与开发转换阶段

哈里斯鹰优化算法从全局搜索与局部搜索的转换主要依靠逃逸能量因子

E

来控制，其定义如下：

其中：

E

为在（-1，1）的能量迭代初始值；

T

表示最大迭代次数。当 |

E

|≥1 时，HHO 算法将进行全局搜索，表示整个种群随着猎物在整个搜索空间中移动；当|

E

|＜1 时，HHO 算法则转为代表局部搜索的开发阶段。

1.3 开发阶段

在对目标猎物完成包围后，鹰群在开发阶段将进行攻击。根据猎物的逃逸行为和哈里斯鹰的追逐策略，HHO 算法使用四种不同的策略来模拟攻击，并通过逃逸能量因子

E

和随机数

r

∈(0，1)来决定使用的策略，

r

是猎物的逃脱机会，

r

＜0.5 表示成功逃脱，

r

≥0.5 则是未能成功逃脱。

1.3.1 软包围

当 |

E

|≥0.5 和

r

≥0.5 时，猎物有足够的体力，试图通过跳跃逃脱，但最终被捕获，公式如下：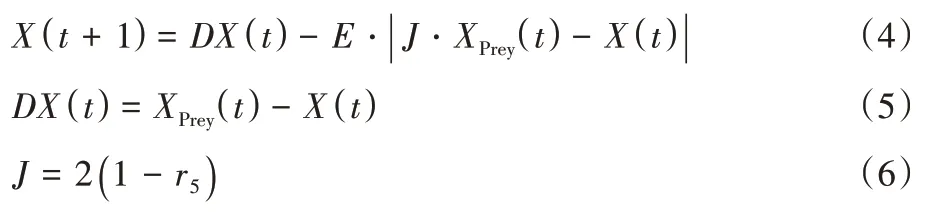

其中：

DX

（

t

）为最优个体和当前个体的距离，表示第

t

次迭代后鹰群与猎物的位置偏差；

r

为（0，1）的随机数；

J

为猎物逃跑过程中的跳跃距离。

1.3.2 硬包围

当 ||

E

＜0.5 和

r

≥0.5 时，猎物没有充足的能量，被鹰直接捕获，公式如下：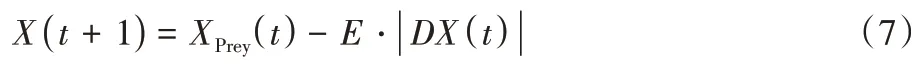

1.3.3 快速俯冲的软包围

当|

E

|≥0.5 和

r

＜0.5 时，猎物逃逸能量充沛有机会逃脱，因此鹰群形成一个更加智能的软包围圈，实施策略如下：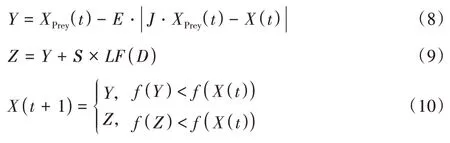

其中：

D

为问题维度；

S

是一个

D

维的随机向量；

LF

为Levy 飞行函数。计算公式如式（11）所示：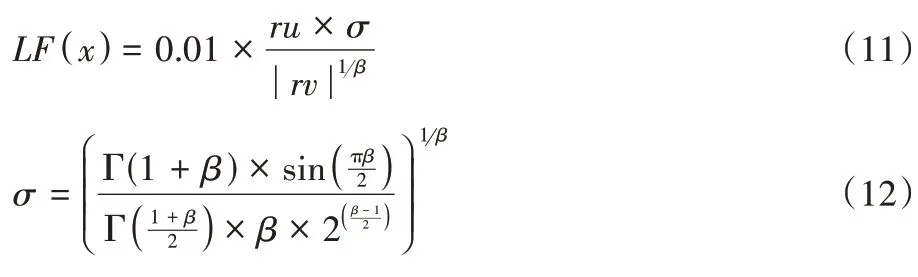

其中：

ru

和

rv

为（0，1）的随机数，

β

是值为1.5 的常量。

1.3.4 快速俯冲的硬包围

当 |

E

|＜0.5 和

r

＜0.5 时，猎物体能不足，但仍有机会逃脱。因此鹰群形成一个硬包围圈，缩小与猎物的平均距离，采用以下策略进行狩猎：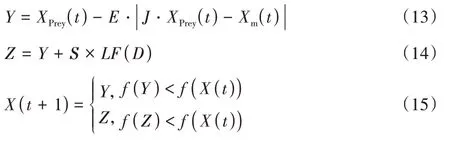

2 改进的HHO算法

为了克服经典HHO 算法存在的缺陷，并提高其寻优性能，本章将从以下几个方面阐述采用的优化方法。

2.1 识别收敛趋势

在寻优过程中，收敛曲线能够描述每次迭代的搜索结果及其变化轨迹，所以，分析曲线的变化趋势并采取相应的处理机制可以有效防止搜索陷入局部最优。本节对收敛曲线的趋势和分类进行说明，并对识别方法和分类规则进行阐述。

1）设相邻两次迭代之间搜索到最优解的下降率为

HuntStep

，其数学公式如下：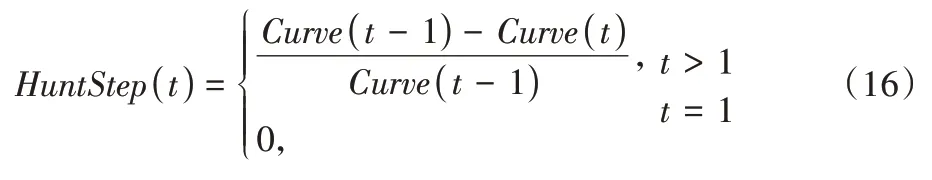

其中：

t

为迭代计数，

Curve

（

t

）为第

t

次迭代搜索到的最优解。2）设最优解变化权重

StepValue

，其值受迭代计数

t

和最优解下降率

HuntStep

的影响，见表1。

表1 最优解变化权重Tab 1 Change weight of optimal solution

3）针对不同的寻优阶段统计不同数量的最优解变化权重之和

TreadStatus

，公式如下：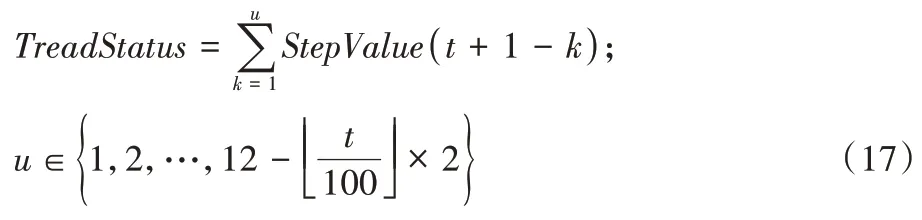

4）根据

TreadStatus

的值，识别收敛曲线变化趋势

ConvergenceState

，如表2 所示。

表2 收敛曲线变化趋势说明Tab 2 Explanation of change trend about convergence curve

使用

u

个最优解变化权重之和来分析收敛曲线的变化趋势，是为了排除个别记录偏离总体趋势而导致的误判。结果表明，该方法能够较好地预判陷入局部最优的可能性，有助于最终得到更优解。

2.2 趋化校正

在HHO 算法中，一个搜索代理每次迭代中只能移动一次位置。本节利用BFO 算法的CC 机制，提高HHO 局部搜索能力。由于CC 会增加算法寻优的时间消耗，为了平衡寻优精度和效率，只在软包围和硬包围两种策略中，且收敛曲线状态

ConvergenceState

处于“平缓下降”的前提下，才进行CC。设随机方向向量

δ

，其每个元素的取值范围为（-1，1），定义如下：

设随机游动方向

φ

定义如下：

通过趋化机制对搜索代理的位置进行校正，设

che

的定义如下：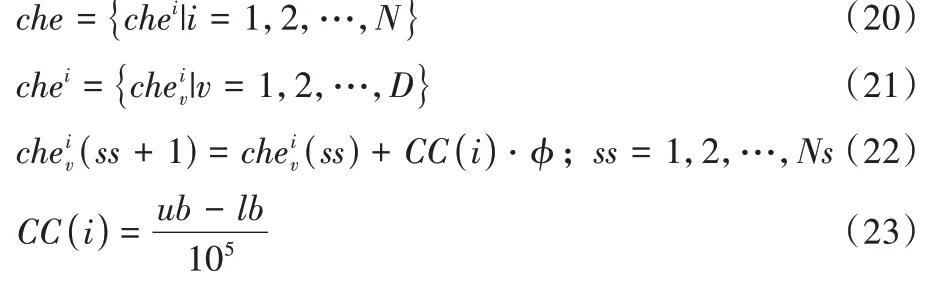

其中：

CC

（

i

）为HHO 中第

i

个搜索代理的游动步长；

D

是每个搜索代理的维数；

v

是第

v

个变量。反复游动，直到趋化计数器

ss

达到最大游动步数

Ns

。若

f

（

che

）＜

f

（

X

（

t

）），则

与经典的HHO 算法相比，此方法使搜索代理有更多的移动机会，因此更有可能获得最佳结果。

2.3 基于生物能量消耗的逃逸能量因子E与跳跃距离J

在HHO 算法中，逃逸能量因子

E

反映对问题最优解的搜索能力、决定着全局搜索和局部搜索的切换、影响着开发阶段所采用的策略，其在寻优过程中表现为线性递减的状态。Gupta 等提出的m-HHO 优化算法为了使搜索获得更多处于开发阶段的机会，设置非线性能量因子

E

如下：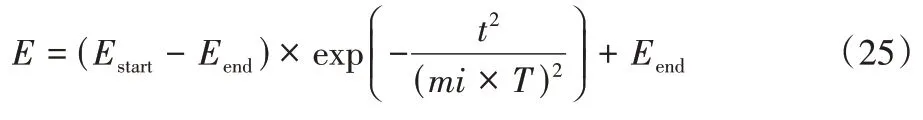

其中：

t

为当前迭代计数；

T

为最大迭代次数；

mi

为非线性调制指数；

E

和

E

分别为初始和最终能量参数值。

m-HHO 虽然在探索阶段将获得较好的结果，但是因其放弃的随机因子，使得算法在广泛性和鲁棒性上有所下降，且以上两种算法均不符合猎物在逃跑过程中的能量消耗与恢复，以及鹰群与猎物间的多轮博弈的实际情况。猎物在逃跑过程中随着奔跑距离的增加体能迅速下降，在体能消耗到极限的条件下，通过短暂的休息或停留可以获得一定程度的恢复，将这个往复、循环的过程描述为如下公式：

其中：

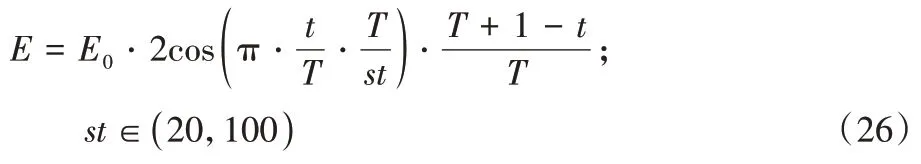
E

的含义与式（3）相同；

st

为（20，100）的随机数，决定着猎物在逃跑过程中进行体能恢复的次数。

由图1 可知，猎物在被追捕过程中的体能消耗的总体趋势呈下降状态，而且随着时间的推移，体力恢复的上限将会越来越低、恢复所需时间越来越长。

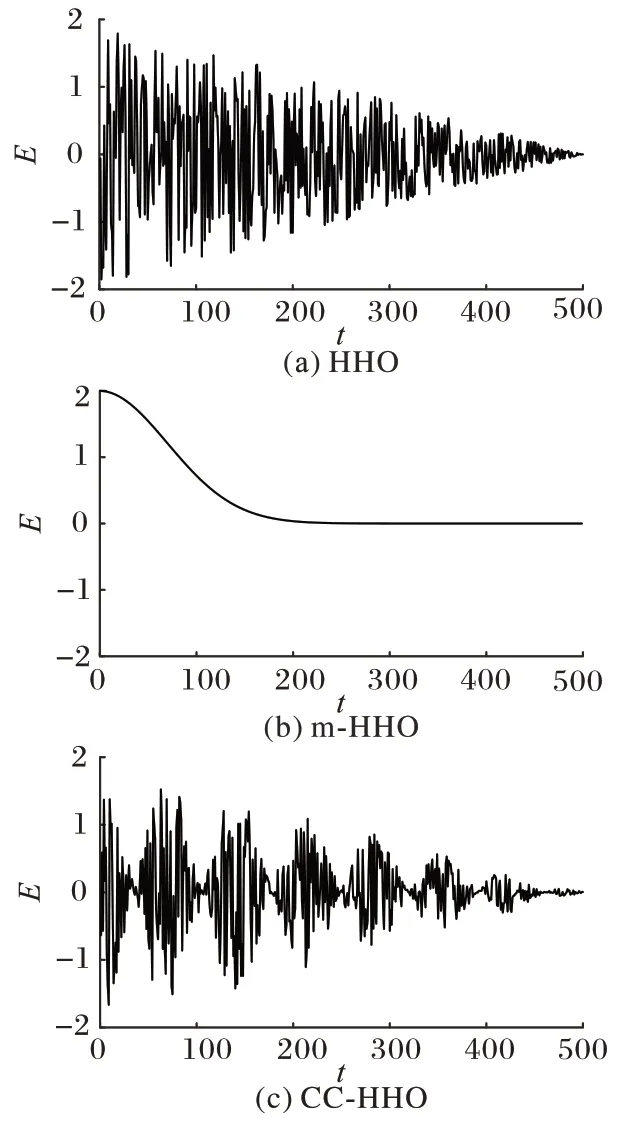
图1 逃逸能量因子E的变化曲线Fig.1 Change curve of escape energy factor E

逃逸能量因子

E

的变化必然导致其在逃跑过程中的跳跃距离

J

产生相应的变化，针对逃逸能量因子|

E

|与0.5 的关系，设置

J

如下：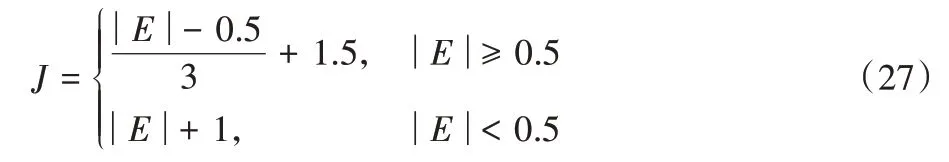

如图2 所示，下方曲线为逃逸能量因子

E

，上方曲线为跳跃距离

J

。可见，

E

与

J

的变化是一一对应的，猎物在体能充沛时，跳跃距离较远；体力耗尽时，几乎跳不动；更加符合生物规律。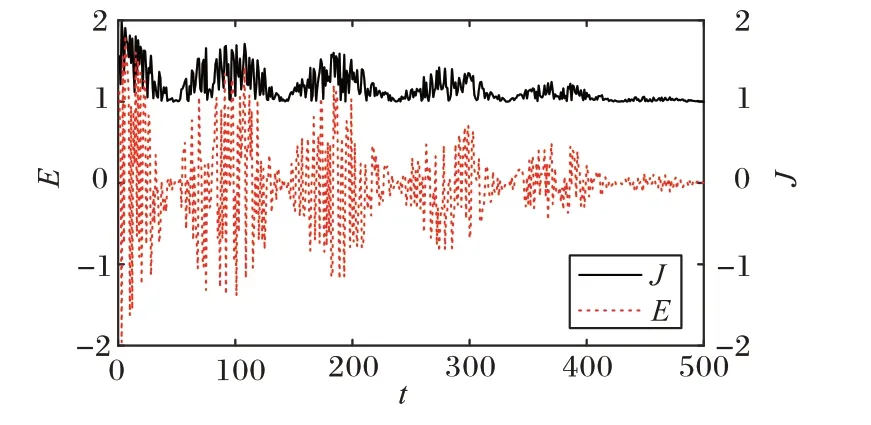

图2 逃逸能量因子E与跳跃距离J的关系Fig.2 Relationship between escape energy factor E and jump strength J

2.4 精英选择

为了提高HHO 算法的收敛精度和全局搜索能力，本节在迭代过程中不仅仅记录搜索到的最优解，同时将次优解引入寻优过程，用于引导其他个体的移动方向。

设

X

和

X

分别为通过迭代得到的最优解和次优解所处的位置，根据精英选择机制计算以

X

（

t

）、

X

和

X

两两组合作为参数，生成的新位置集合

LocationES

，计算公式如下：

分别计算集合

LocationES

中三个新位置的代价函数适应度值，并取出最小值，如式（32）所示：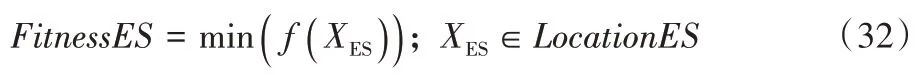

若

FitnessES

＜

f

（

X

（

t

）），则同时更新

X

（

t

）、

X

和

X

。

2.5 强制进入探索阶段

在迭代后期，如果收敛曲线的状态为“平缓下降”或“水平线”，则说明搜索即将陷入局部最优或已经陷入局部最优，通过令逃逸能量因子

E

=1，强制使寻优切换到全局探索阶段。根据随机数

q

的值，搜索代理向上限或下限大范围移动，公式如下：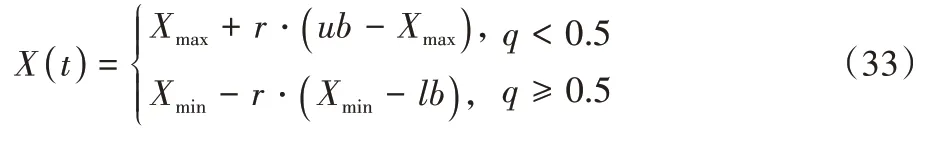

其中：

X

和

X

分别为种群中距种群的平均位置

X

最远和最近的个体；

r

是位于（0，1）的随机数；

ub

和

lb

分别为上下限。当

q

＜0.5 时，搜索代理在

X

和上限之间选择一个位置；

q

≥0.5 时，在

X

和下限之间选择一个位置。

3 算法伪代码与时空复杂度分析

3.1 算法伪代码

本节对上述改进方法在原始HHO 算法中的应用以伪代码形式进行说明。

输入 种群规模

N

、最大迭代次数

T

。

输出 猎物的位置和其适应度值。

3.2 时间复杂度分析

设改进算法的种群规模为

N

，迭代

T

次，按照算法的执行步骤进行算法时间复杂度分析。1）鹰群初始化，需进行

N

次操作，时间复杂度为

O

（

N

）。2）计算收敛趋势，计算2 次，时间复杂度为

O

（2）。3）计算函数适应度，时间复杂度为

O

（1）。4）进行精英选择求得最优解，需要6 次计算、2 次比较，时间复杂度为

O

（8）。

5）执行群行为。

5.1）计算

E

与

J

，时间复杂度为

O

（2）。5.2）根据收敛趋势，判断是否进入强制探索，比较1 次，计算1 次移动1 次，时间复杂度为

O

（3）。5.3）确定进入探索或开发，比较1 次，时间复杂度为

O

（1）。5.4）在探索阶段，比较1 次，移动1 次，时间复杂度为

O

（2）。5.5）在开发阶段，比较1 次，确定鹰群的攻击策略，移动1 次，时间复杂度为

O

（2）。5.6）趋化校正，计算3 次，比较1 次。趋化过程中需要试探

MaxStep

次，时间复杂度为

O

(4+

MaxStep

)。步骤5）循环

N

次，因此其时间复杂度为

O

((14 +

MaxStep

)*

N

)。经历上述步骤后，改进算法在

T

次迭代后的时间复杂度为：

O

(

T

*(14 +

MaxStep

)*

N

)。

3.3 改进算法空间复杂度分析

空间复杂度是用算法执行时占用存储空间来衡量的，设鹰群的规模为

N

，迭代次数为

T

，需要求解的函数的维数为

D

，按照算法步骤进行空间复杂度分析。在改进算法中，

X

［

N

］［

D

］存储种群初始化值，

X

［1］［

D

］存储优化的自变量，

Fitness

存储优化函数值，

LocationES

［3］［

D

］存储3 个精英自变量，

FitnessES

［3］［1］存储3个精英函数值，

HuntStep

［1］［

T

］存储每两次迭代之间的结果差，

StepValue

［1］［

T

］存储每次迭代结果评分，

X

［1］［

D

］存储种群中随机选择的搜索代理所在位置，

X

［1］［

D

］存储种群的平均位置，

δ

［1］［

D

］存储随机方向向量，

che

［

N

］［

D

］存储趋化修正值。因此，整个改进人工鱼群算法的空间复杂度为：2*

O

(

N

*

D

)+7*

O

(

D

)+2*

O

(

T

) +

O

(3)。

4 实验与结果分析

本节通过10 个基准函数，使用Intel i7-4790、8 GB 内存的计算机在Matlab 2012b 仿真平台上对CC-HHO 算法的寻优性能进行测试，并给出实验结果及分析。基准函数分为3 类：F1～F4 为单峰函数，用于评估元启发式算法的开发能力；F5～F8 为多峰函数，F9～F10 为定维多峰函数；F5～F10 均具有一个以上的局部最优解，变量数量以指数形式增加，用于对算法的探索能力和对局部最优的规避能力进行评价。函数编号、函数名、变量数、变量边界和理论最优解如表3 所示。

表3 基准函数信息Tab 3 Information of benchmark functions

4.1 CC-HHO算法与其他元启发式优化算法比较

本节将CC-HHO 算法与包括经典HHO 算法在内的其他4 种元启发式优化算法GSA、PSO、WOA和HHO进行比较。为了便于不同算法进行横向比较，所有实验参数均采用和原始HHO 算法相同的设置，即：种群数为30，迭代次数为500。为了平衡算法时间复杂度和局部搜索的细致性，趋化操作中单向运动的最大步数

Ns

为4。每组测试包含30轮，记录均值、标准差、最优值和最差值，测试结果见表4。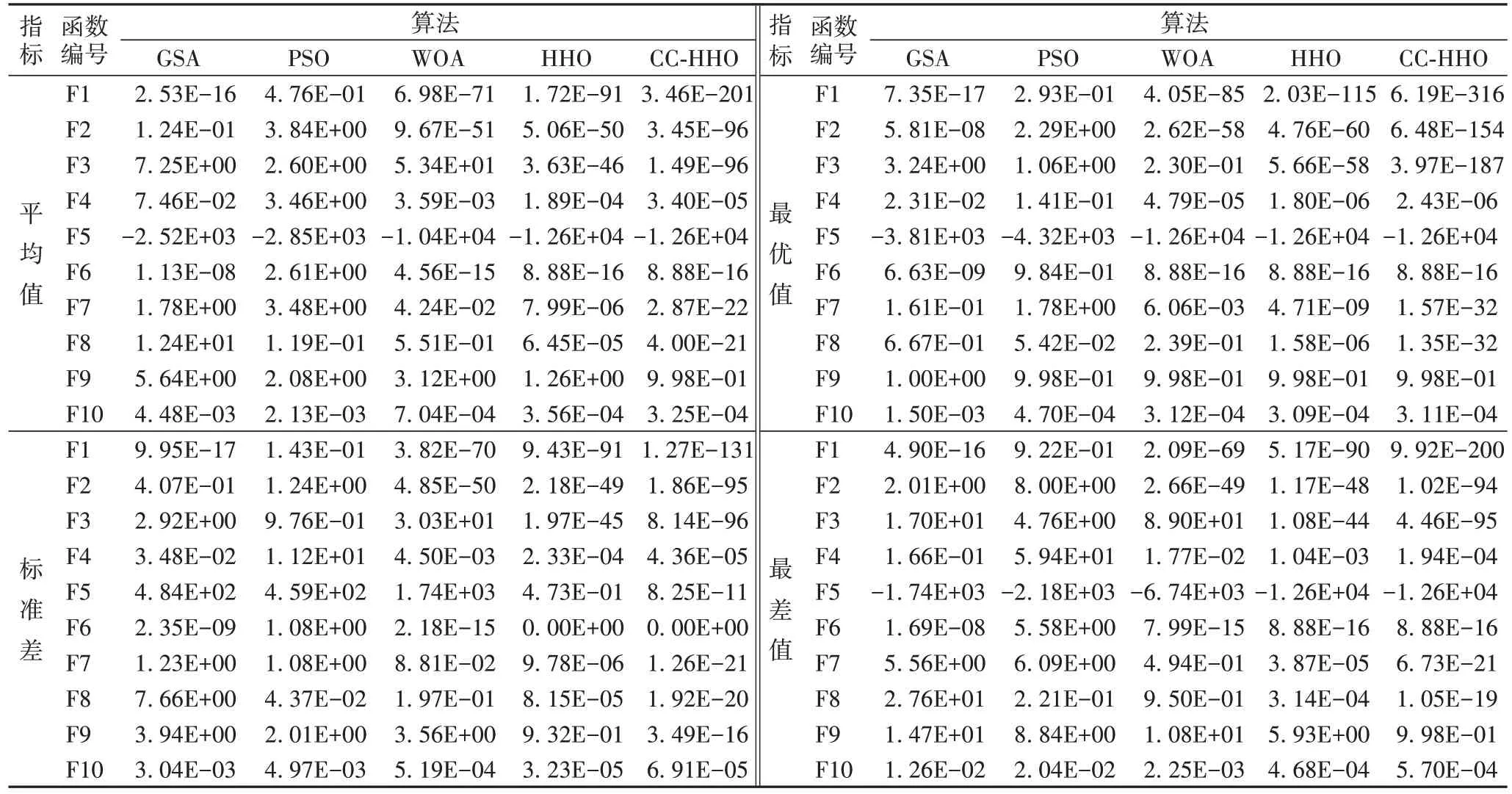

表4 CC-HHO 与其他元启发式算法的寻优结果比较Tab 4 Optimization result comparison between CC-HHO and other meta heuristics algorithms

本文所提出CC-HHO 算法的寻优能力与其他4 种算法相比都具有很强的竞争力。对于单峰测试函数F1～F4，CCHHO 的平均值和标准差都大幅优于包含HHO 在内的其他4种算法，不但最终结果更好，而且算法稳定性更优。在多峰函数和定维多峰函数方面，从F5～F6 来看，CC-HHO 的均值与HHO 持平，优于GSA、PSO、WOA；从F7～F10 来看，CCHHO 获得令人满意的结果，相对于HHO 具有小幅优势。

4.2 CC-HHO算法与其他改进HHO算法比较

本节将CC-HHO 算法与其他4 种改进的HHO 算法CEHHO、IHHO、HHOA-OBL、HHO-SQP进行性能对比分析，迭代次数为500，每种算法对每个函数进行30 次测试，收集均值、标准差、最优值和最差值作为评价依据，测试结果如表5 所示。

如表5 所示，CC-HHO 算法在函数F1～F4 的平均值和最优值表现上完全压制其他4 种改进的HHO 算法。对于F5～F6，因为5 种改进算法都是从HHO 算法的衍生而来，所以搜索性能指标基本相同。从函数F7～F10 的结果来看，虽然CC-HHO 算法在数量级上没有形成巨大优势，但与其他函数相比仍然更加优秀。结果表明，CC-HHO 算法的准确度和鲁棒性都优于其他改进算法。

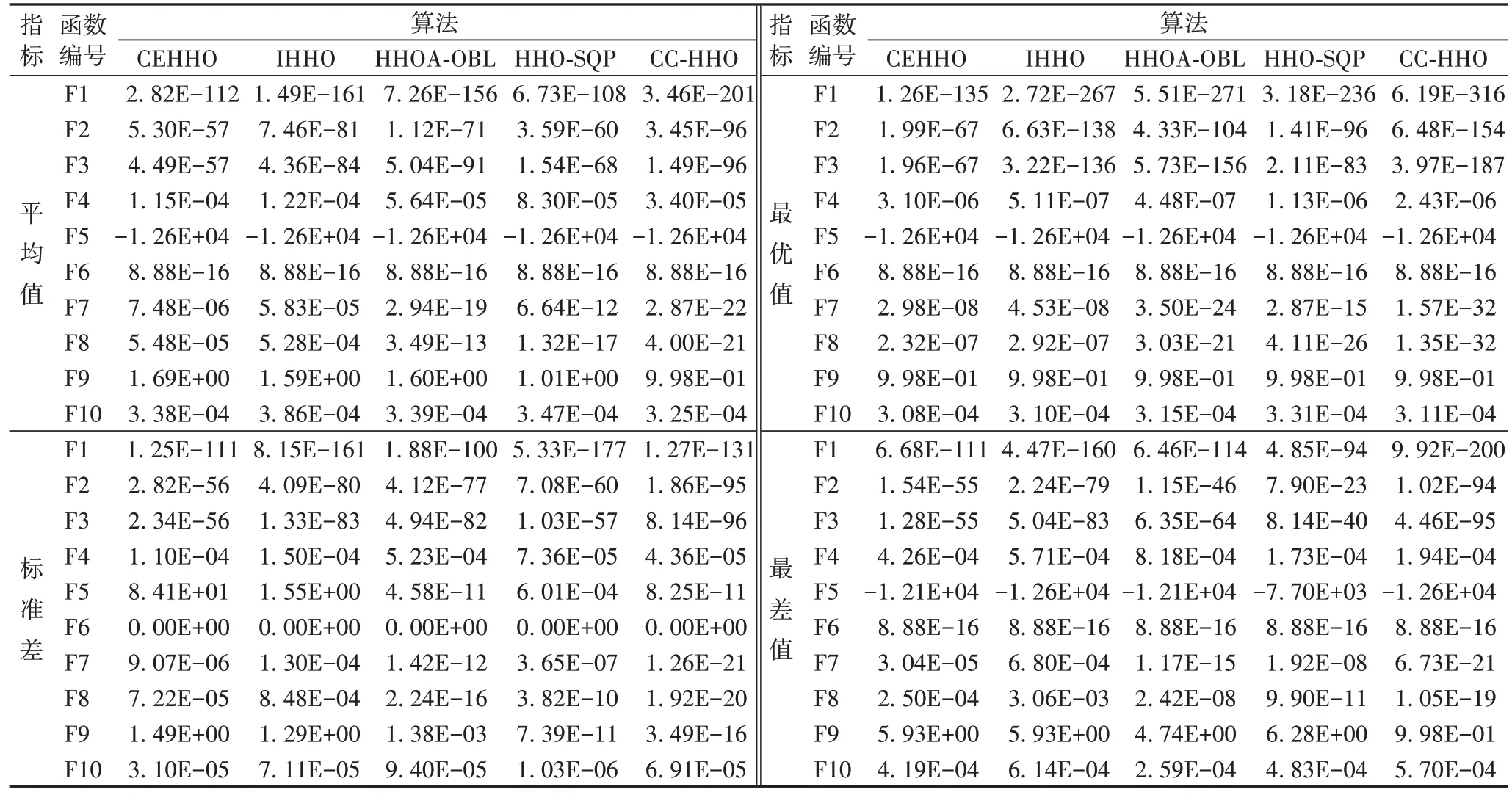
表5 CC-HHO 与其他改进HHO算法的寻优结果比较Tab 5 Optimization result comparison between CC-HHO and other improved HHO algorithms

图3 是单峰基准函数的收敛曲线，在5 种改进的HHO 算法中，CC-HHO 算法的最终寻优结果最好。F1 和F4 的收敛速度最快，收敛精度最高。在F3，虽然CC-HHO 算法的收敛速度相对较慢，但是依然在寻优后期通过CC 找到更优解。在F4，能够明显看出CC-HHO 算法在迭代初始阶段就快速收敛并经历至少两次陷入局部最优，但通过“强制探索”跳出。

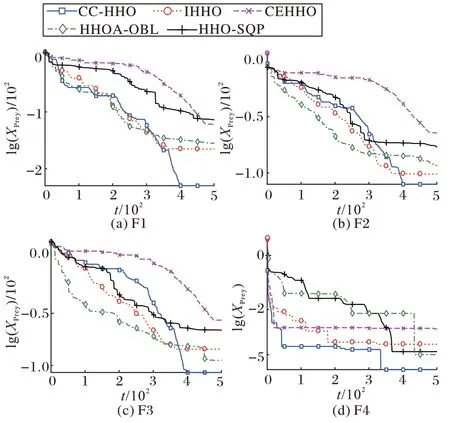
图3 单峰函数的收敛曲线Fig.3 Convergence curves of unimodal functions

图4 是多峰基准函数的比较，对于F7，CC-HHO 算法比HHO-SQP 和HHOA-OBL 收敛速度稍慢；对于F5、F6、F8，CCHHO 算法收敛最快，收敛精度也很突出，当其他改进的HHO算法陷入局部最优，没有机会搜索到更好的解时，CC-HHO 算法通过分析收敛趋势、精英选择、趋化校正寻找到更优解。

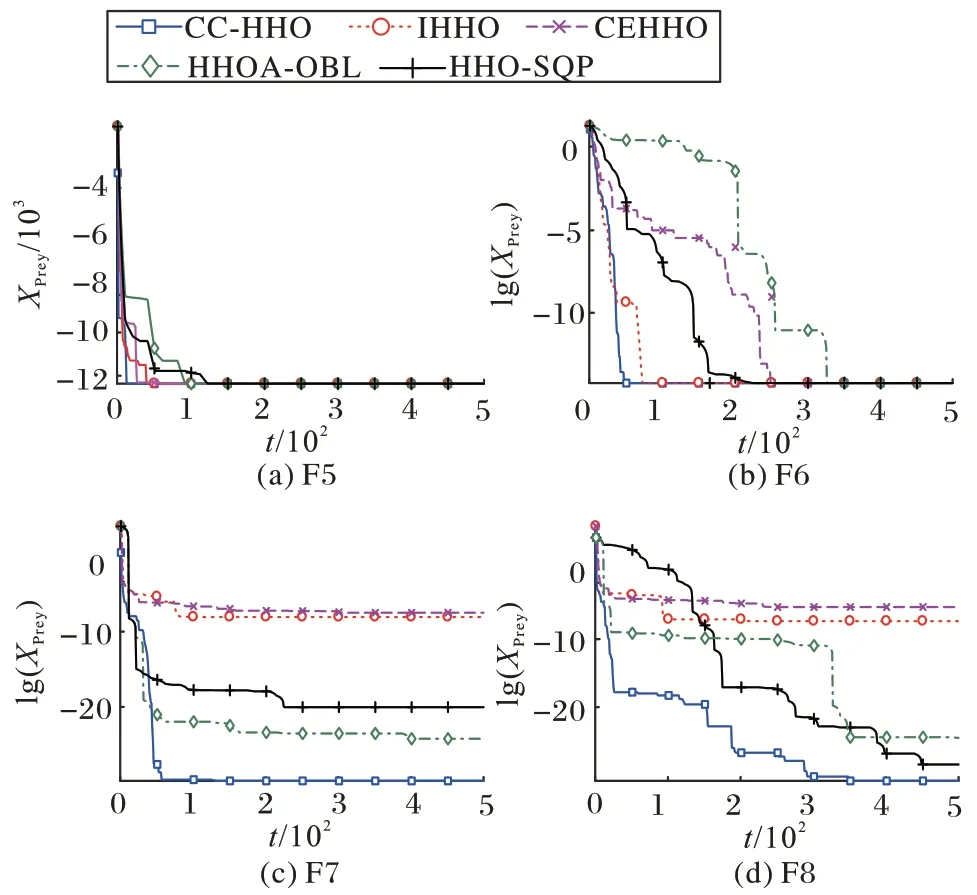
图4 多峰函数的收敛曲线Fig.4 Convergence curves of multimodal functions

图5 为5 种改进的HHO 算法在定维多峰函数F9～F10 的寻优收敛曲线，最终寻优结果处于同一数量级。F10 表明CC-HHO 算法具有最佳的收敛速度和最终解。

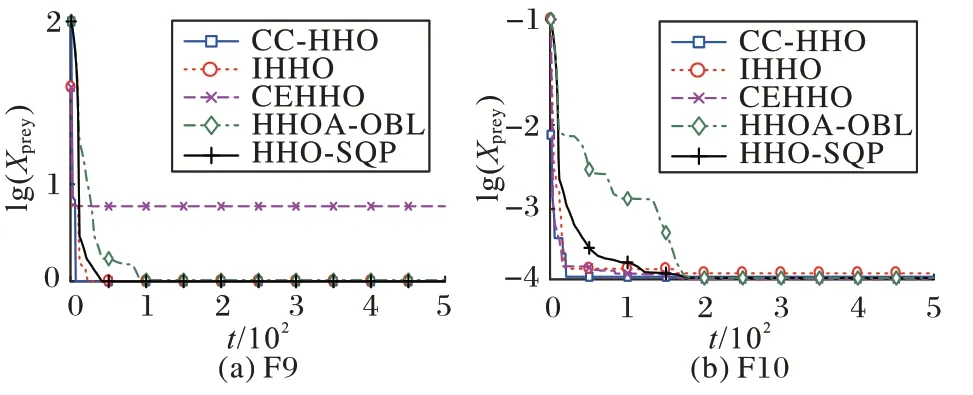
图5 定维多峰函数的收敛曲线Fig.5 Convergence curves of fixed-dimensional multimodal functions

5 结语

为了克服HHO 算法的缺点，提高算法的寻优性能，通过识别收敛曲线状态、趋化校正、引入基于生物能量消耗的逃逸能量因子、精英选择、强制探索的途径进行优化和提出改进算法。并通过10 个基准函数进行测试。对比其他元启发式算法和改进的HHO 算法，仿真结果和收敛曲线表明，本文CC-HHO 算法在单峰函数上展现出超强的寻优能力；在多峰函数和定维多峰函数上，除所有参与比较算法均能找到理论最优解的情况，本文CC-HHO 算法在收敛精度上具有一定优势。综上说明，本文算法在探索、开发和避免局部最优方面具有竞争力，提高了原算法的搜索效率和鲁棒性。但是多模态基准函数的寻优表现不如单峰基准函数，有待于进一步研究。