基于多属性综合评价的食品安全标准引用网络重要节点发现方法

郝志刚，秦 丽，2*

（1.华中农业大学信息学院，武汉 430070；2.湖北省农业大数据工程技术研究中心（华中农业大学），武汉 430070）

0 引言

食品安全国家标准的起草和实施是我国食品安全体系建设中重要的一环。随着食品行业的发展以及食品安全体系建设的不断完善，现有的食品标准数量已经达到上千个。普通民众很难对这些食品标准有一个清晰的认识，而且由于我国食品安全标准体系仍不完善，各标准之间不协调统一，这导致标准的审查和执行上也存在问题，特别是标准更新周期的不一致，有些标准更新周期长，标准的版本较早；有些标准更新周期短，存在多个标准。食品生产企业和食品质检部门如果对这些标准的认识不统一，将会导致同时执行多个标准，对我国的食品生产和检测造成严重影响，进一步危害我国的食品安全体系建设。而造成这一结果的原因主要是食品安全标准数量较多，种类繁杂，标准之间存在着较多的引用关系，对食品标准的修订带来很大难处，尤其是那些占据着核心地位的食品标准，对这些标准的修订“牵一发而动全身”。对食品生产企业来说，准确把握众多标准中的核心标准对指导食品生产是很有必要的。为了找出这些隐藏在所有食品安全标准中的“核心标准”，需要利用食品安全标准引用网络来从众多的食品安全国家标准中找到对食品安全检验、检测影响较大的关键标准，因此本文提出了一种基于多属性综合评价的食品安全标准引用网络重要节点的发现方法。

网络模型是对现实世界中事物以及事物之间的关系的抽象，网络中的节点和边分别表示事物和关系，通过分析网络，可以得到很多有用的信息来进行下一步研究。其中，最具代表性的工作就是社交网络分析。而食品安全标准引用网络虽然节点只有一千多个，但节点间的引用关系比较复杂，因此社交网络节点的分析方法也可以应用到食品标准引用网络中。基于这一想法，本文使用社交网络中评价节点重要性的一些指标，如度中心性（Degree Centrality，DC）、紧密度中心性（Closeness Centrality，CC）、介数中心性（Betweenness Centrality，BC）等，并结合PageRank（PR）页面重要性算法来对标准节点的重要性进行综合评价，以此来判断哪些食品安全标准属于“核心标准”。

1 相关工作

近年来，社交网络的研究领域越来越广泛。在这些研究中，对网络节点重要性进行排序是一项重要工作。基于此，诞生了一些经典的排序方法，如度中心性、半局部中心性、紧密度中心 性、Katz中心性、介数中心性、PageRank等其他算法。郑文萍等提出了节点中心性度量指标LNC（Local Neighbor Centrality）识别网络中的关键节点；罗浩等提出了采用信息融合的IOMEC（In-degree Out-degree Multiplex Evidential Centrality）节点重要性度量方法；杜航原等提出利用节点的内聚度和分离度计算节点重要性；马媛媛等提出KI（K-shell Intimacy）算法计算节点的亲密度从而对节点重要性进行排序；邵豪等提出H 算法识别动态网络中的重要节点；尹荣荣等融合了结构洞与K核指标来对网络节点重要度进行评估；梁耀洲等通过排名聚合的方法来挖掘社交网络中的关键用户。随着社交网络相关研究的成功，研究人员将目光转向了其他领域内的复杂网络研究，并将社交网络研究中的一些成果直接应用到其他网络中，如物流配送节点重要性、公路网络节点重要性等，且取得了不错的研究成果。

2 重要性评价指标

2.1 度中心性

节点度数是节点周围的邻居节点数目，在有向图中包括出度（指向其他节点的边的数目）和入度（进入该节点的边的数目），是评价一个节点重要性最为直观的指标。节点度数越大表明与之直接相连的节点也越多，该节点重要性程度也就越高。而度中心性（DC）则是根据网络中节点总数对节点的度进行标准化。假设在网络

G

中共有

N

个节点，其中，节点

x

共有

k

个节点与之直接相连，则记该节点度数为

deg

(

x

)=

k

，对应的度中心性计算为式（1）：

但是，这一指标只能表明节点在局部小范围内的重要程度，没有考虑节点在网络中所处的位置信息。因此，需结合其他评判标准来综合考虑节点的重要程度。

2.2 紧密度中心性

节点紧密度表示节点与网络中所有节点的紧密程度，即节点到其他节点的距离总和越小，紧密度越高。而紧密度中心性（CC）则是利用节点总数对节点紧密度进行标准化。假定节点

x

和节点

y

之间的距离用

d

(

x

，

y

)来表示，则

x

的紧密度中心性计算如式（2）：

2.3 介数中心性

节点的介数用来反映节点在网络中所处位置的重要程度，途经某节点的最短路径越多，该节点的介数越大。同样，介数中心性（BC）则是利用节点数目对其进行标准化。假定节点

x

和节点

y

之间的最短路径数为

σ

(

x

，

y

)，其中通过节点

i

的数目为

σ

(

x

，

y

|

i

)，则节点

i

的介数中心性计算如式（3）：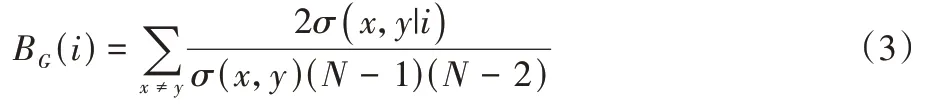

2.4 PageRank

PageRank（PR）算法是Google 应用在搜索引擎中来判断Web 页面重要度的一种算法。一个页面的重要程度由指向该页面的其他页面数目以及页面相应的重要程度决定。将其应用到网络中，则表明一个节点的重要程度由相邻节点数目和节点对应的重要程度决定，通过多次迭代，最终确定每一个节点的重要程度。对于一个节点

v

其PR 值计算如式（4）：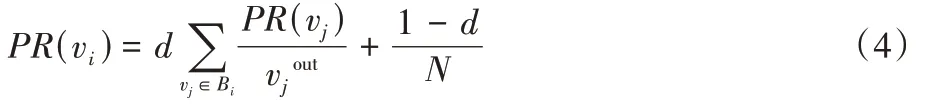

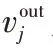
3 食品标准引用网络构建

食品安全标准引用网络的构建主要由两部分工作组成：一个是节点的抽取，另一个是节点间关系的抽取。

3.1 节点抽取

食品安全标准引用网络的节点名称由食品标准的标准编号表示，该编号是独一无二的，因此每个节点都代表一种食品安全标准，节点抽取本质上就是对每个食品安全标准的编号进行抽取。而食品安全标准的编号组成是有规律的，比如：1）每种标准编号以“GB”开头，表示国标；2）“GB”之后是每种标准对应的特殊数字串；3）最后是每种标准的发布时间。根据这些信息，可以通过正则式将其提取出来。

3.2 关系抽取

食品安全标准之间的引用关系隐含在标准文档的内容中，经过数据处理后的文本和表格信息作为关系抽取的原始数据，使用一些简单的自然语言处理技术就可以将食品标准引用关系抽取出来。

本文采用了基于规则的模式匹配方法。因为要抽取的关系比较简单，在文档中表述标准之间的引用关系时会写明在哪一方面参考了其他标准，比如，在《GB2717―2018 食品安全国家标准酱油》中在引用其他标准时，相应的描述文本为“污染物限量应符合GB2762 的规定”“真菌毒素限量应符合GB2761 的规定”“致病菌限量应符合GB29921 的规定”等。而类似“污染物限量”“真菌毒素限量”等关键词在其他标准中的描述也大致相同。因此，只需要预先定义关键词库并辅以一些匹配规则即可进行标准引用关系抽取。

在本文的前期工作中，经过节点和关系抽取后，共得到1 239 个节点和2 593 条边，借助可视化软件将其绘制为如图1 所示的引用关系网络。

图1 食品安全标准引用关系网络Fig.1 Food safety standard reference network

图1 中，不同的节点标签显示的文字大小会根据节点的度数大小而改变，节点的度数越大，标签文字越大。

4 节点重要性分析

对食品安全标准引用网络中的节点依据节点的度、度中心性、紧密度中心性、介数中心性分别进行计算，并利用PageRank 算法对每个节点的重要程度进行评价，以下是一些节点的计算结果。

4.1 节点的度

从图1 中可以粗略地看出大部分节点的度数比较小，有少部分节点度数较大，此外，还列出了排名前十的节点相关信息（表1）。在表1 中，度数排名靠前的节点如GB5009.12、GB/T14454、GB/T6682―2008、GB/T11538―2006、GB/T11540、GB/T14455 等节点度数在100 以上的食品安全标准，在图1 中展示较为清晰。而这些节点的出度全为0，说明这些节点的度数全部来源于节点入度，也表明了这些标准被其他标准引用较多，从侧面证明了这些食品安全标准的重要程度。

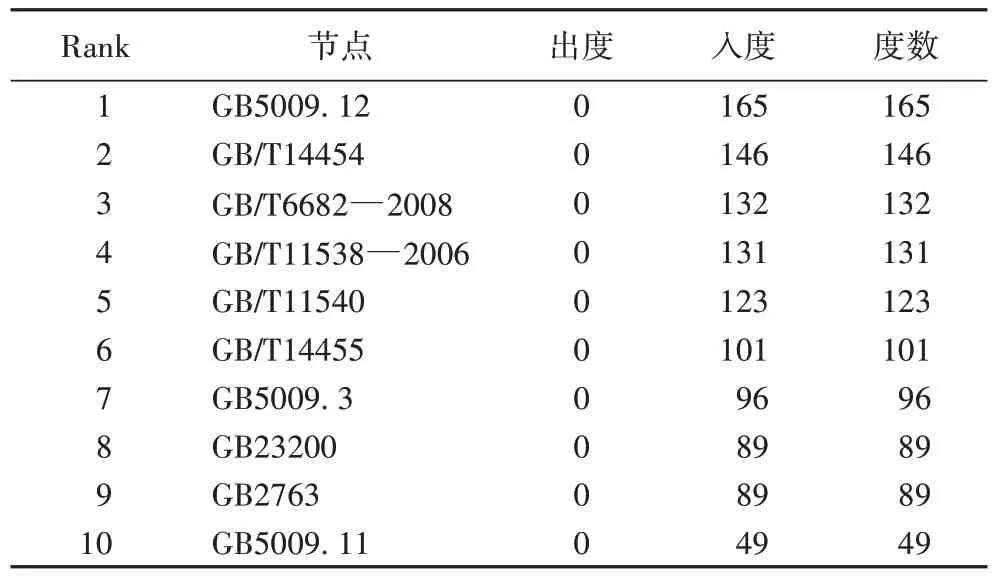
表1 食品标准引用网络节点度数（Top10）Tab 1 Degrees of food standard reference network nodes（Top10）

4.2 度中心性

DC 是对节点度数进行标准化，经过标准化后的度中心性值可以反映某一节点的邻居节点数目在总节点中的占比情况。表2 列出了食品标准引用网络节点的前十位。

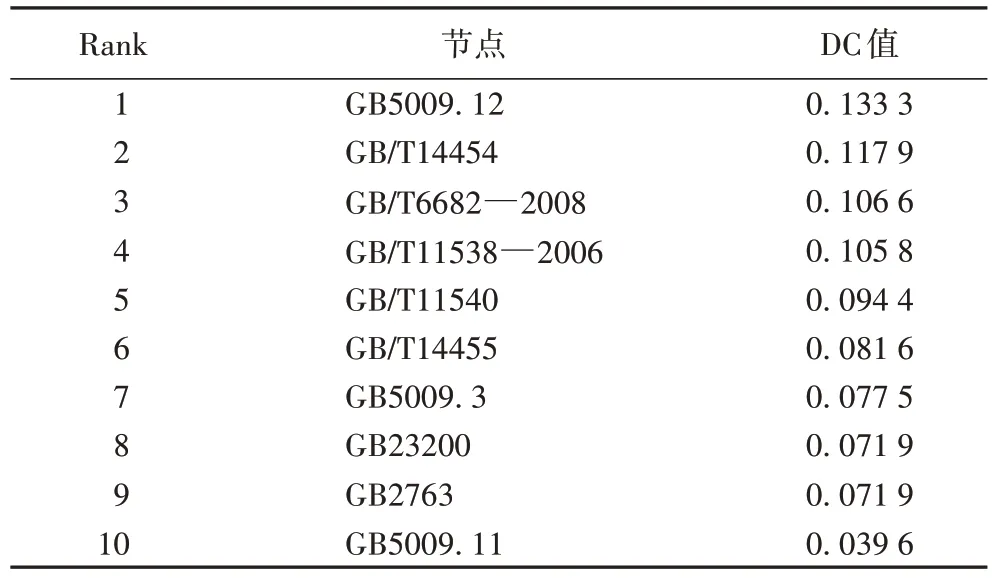
表2 食品标准引用网络节点的DC值（Top10）Tab 2 DC values of food standards reference network nodes（Top10）

从表2 中可以看出，排名前四的节点GB5009.12、GB/T14454、GB/T6682―2008 和GB/T11538―2006 的引用标准数量达到了所有标准的10%以上，远超过其他的标准，表明这几个标准在所有标准中占据着重要地位。

4.3 紧密度中心性

节点的紧密度反映了节点在整个网络中所处的“中心程度”。经过计算，本文列出了一些节点的CC 值（表3），这些节点之间的CC 值差异不大且数值较小，而从图1 中也可以看出该引用网络中仍然存在着不少的孤立节点，这表明整个网络连通度较低，并没有一个节点能够辐射整个网络，少部分节点只能影响局部的一些节点。

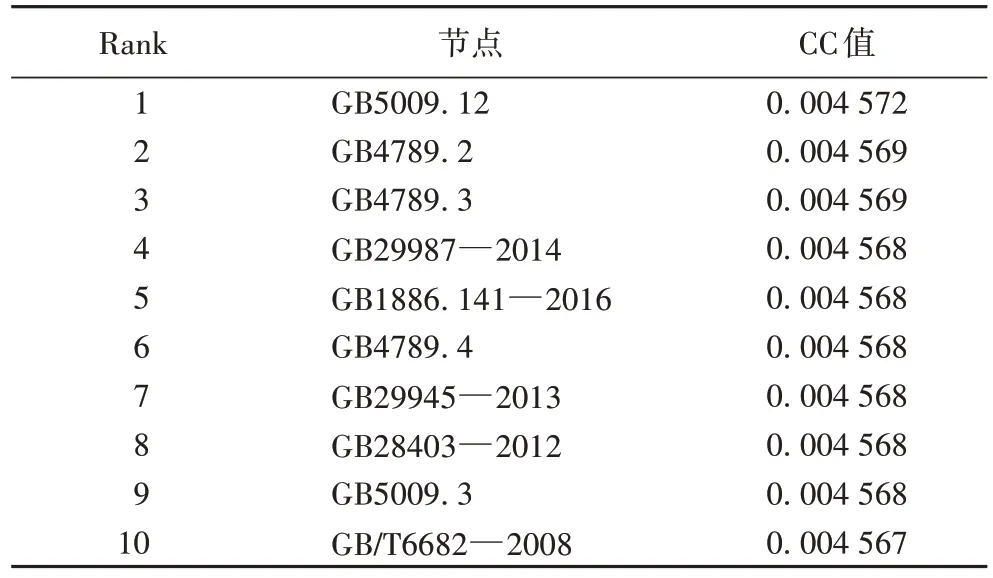
表3 食品标准引用网络节点的CC值（Top10）Tab 3 CC values of food standard reference network nodes（Top10）

4.4 介数中心性

节点的BC 反映了节点在网络中所处位置的重要程度，节点的BC 值越高，表明该节点处在越多的“关键路径”上，该节点在网络中的地位越高。表4 只列出了5 个节点的相应数据，这是因为其他节点的介数中心性值为零。而且5 个节点的介数中心值也较小，这也从侧面反映出整个标准引用网络的连通程度较低，相应的关键路径数目也较少。

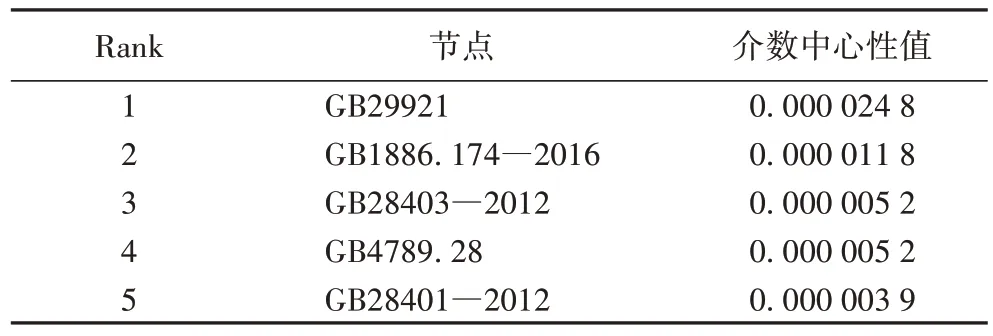
表4 食品标准引用网络节点的BC值（Top5）Tab 4 BC values of food standards reference network nodes（Top5）

4.5 PageRank重要度

PR 算法是谷歌用来对网页进行重要度排序的一种算法，其核心思想是：一个网页的重要程度由这个网页所指向的目标网页以及指向本网页的其他网页的重要程度所共同决定。这个算法可以应用到网络中节点重要度分析，即网络中的每个节点重要度由该节点相连的节点重要度所决定。表5 列出了食品标准引用网络中一些重要度排名靠前的节点数据。从表5 中可以看出，有许多DC 排名靠前的节点，如GB5009.12，GB14454，GB/T6682―2008，GB/T11538―2006等，也出现在表2 中，且排名靠前。这表明在该网络中节点的DC 值对使用PR 算法计算的节点重要度也有重要影响。

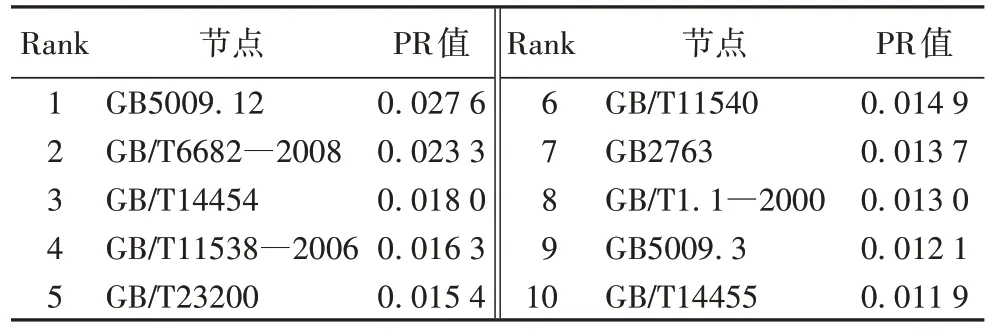
表5 食品标准引用网络节点的PR重要度（Top10）Tab 5 PR importance of food standard reference network nodes（Top10）

4.6 对比分析

为了对标准引用网络的这几个指标从整体上进行分析，本文统计了每种指标相应数值下对应的节点数量，并绘制成图2。从图2 中可以看到，节点的度中心性图像分布、介数中心性图像分布和PageRank 重要度图像分布都呈现一种下降趋势，表明在该引用网络中，大部分节点的重要程度较低，相应的指标值也较小。而紧密度中心性图像分布却呈现两极分化的情况，整个网络中的节点分为了两部分：1）节点的紧密度值较小，代表了网络中那些离散的节点；2）节点的紧密度值较大，代表了网络中那些局部中心点。同时这两部分节点各自的紧密度值差距不大，整体的紧密度值也较小，反映出整个引用网络的连通度不高。此外，度中心性图像分布与PR 重要度图像分布大致相同，表明在该网络中节点的PR 值计算中，节点的度起着重要的作用。

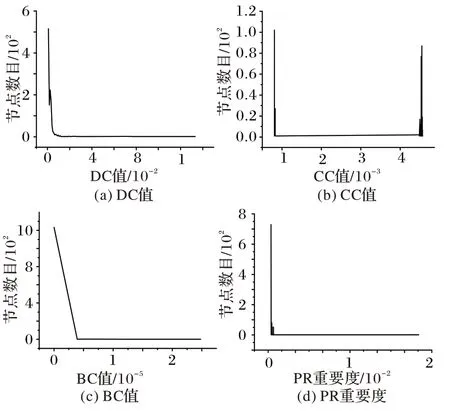
图2 各指标下节点的数量分布Fig.2 Number distribution of nodes under each index

4.7 综合评价

前文给出了评价节点重要性的多个衡量指标，并对每种指标进行了简要的分析，但是仅仅依赖某一指标来判断节点的重要程度存在很大的片面性。因此，要依据这几个指标对节点进行一个综合性的评价，并将评价较高的节点作为标准引用网络中的重要节点，该节点所代表的标准作为重要标准。为了得到每个节点的重要性综合值，首先要确定每种指标的计算权重。

4.7.1 指标权重

对于指标权重的确定可以使用常用的主成分分析法和层次分析法（Analytic Hierarchy Process，AHP）。主成分分析法是在指标数量较多时通过数学变化将指标进行线性组合并选择其中信息量占比大的几个相关性较小的指标作为主成分，并确定主成分的计算权重，在尽可能不影响客观评价的基础上减少工作量；而层次分析法主要依据实验人员的经验来判断指标之间的重要程度，通过构建判断矩阵来确定各指标权重，不对指标进行筛选，对实验人员的经验依赖更强。在后续的节点综合重要性评价中共用到了四个指标，分别为度中心性（DC）、紧密度中心性（CC）、介数中心性（BC）、PageRank（PR）算法。对于这四个指标权重的确定，由于不需要使用主成分分析法来筛选主要指标，同时对于指标之间重要性的判断，实验者的经验要更为重要一些，因此采用了更为适合的层次分析法。利用层次分析法确定各指标权重步骤如下：

1）对于指标

m

与指标

m

(

i

，

j

∈{DC，CC，BC，PR})，使用（0，1，2）三标度法进行两两比较，建立如下比较矩阵

B

：

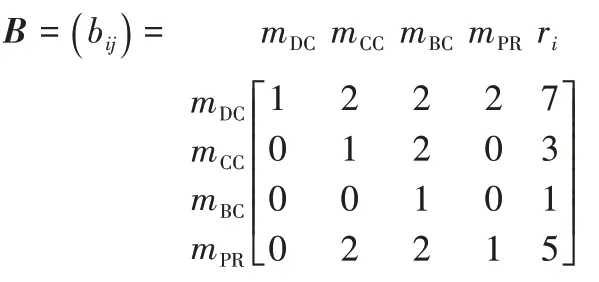
其中：

在比较矩阵

B

中，

m

与

m

、

m

与

m

、

m

与

m

的比较值都为2，表明在4 个指标中，节点的度中心性（DC）是最重要的。主要是因为在食品安全标准引用网络中，节点之间的关系种类比较单一，DC 能够很好地体现出一个标准的重要程度，度越大代表该标准被其他标准引用的次数越多，同时也由于节点关系类型比较单一（只涉及引用关系）且网络中存在着很多的离散节点，而节点的CC 和BC 的计算与整个网络的结构紧密相连，大量离散节点的存在导致整个网络的连通度较低，使得节点的这两个指标计算结果很小，在引用网络中的影响程度较低。从图2 中可以看到，节点的DC 与节点的PR 值图像中的节点分布大致相同，表明这两个指标之间是有一定联系的，节点的PR 值由节点的相邻节点的PR 值不断进行迭代相加计算得出。在该引用网络中，由于只有局部中心点即度数较大的节点周围有其他节点的存在，而每个节点的PR 值主要通过相邻节点的PR 值相加得出，该节点的度数越大意味着通过相加计算得到的节点PR 值就越大，从这一层面来说，节点的PR 值在一定程度上反映了节点的度数；但如果这些局部中心点的相邻节点不再和其他节点相连，也会导致局部中心点的重要度有所下降，这种情况在引用网络中是较为常见的。因此相较于度中心性，节点的PR 值的重要程度要弱一些，但是要比节点的紧密度中心性和介数中心性更重要。因此，本文将

m

与

m

、

m

与

m

的比较值设为2。而

m

与

m

的比较值为2，表明节点的CC 要比节点的BC 重要。从图2 中各指标下节点数量分布来看，几乎所有节点的BC 值为零，而CC 值不为零的节点数量占据了一半以上，表明在该网络中节点的

m

要比

m

更重要些。2）通过变换将比较矩阵

B

转换为判断矩阵

C

并证明满足一致性，最后来确定各指标的相应权重

w

。具体步骤如下：①按照极差法构造判断矩阵

C

。

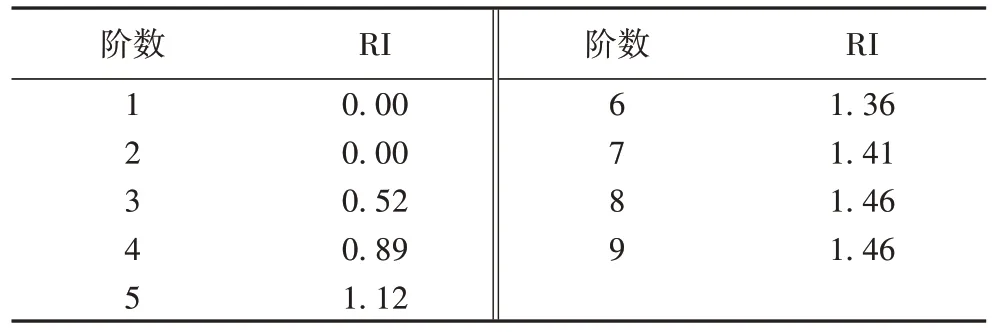
表6 平均随机一致性指标Tab 6 Average random consistency index

经过一致性检验后，最终得到各指标的权重

w

=0.490 8，

w

=0.152 7，

w

=0.083 5，

w

=0.272 9。将利用这些权重来计算每个节点的综合指标重要性。

4.7.2 节点综合指标重要性计算

本文采用的是基于逼近理想解排序法（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）的多属性决策方法。具体计算步骤如下：

利用前文计算得到的各节点对应的指标值以及使用AHP 确定的各指标权重，采用TOPSIS 计算后的

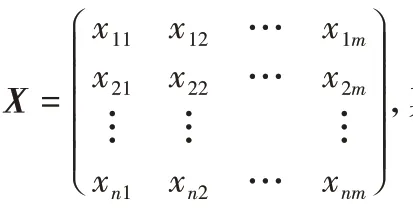
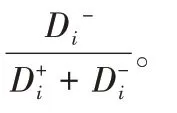
D

、

D

以及

Z

如表7 所示。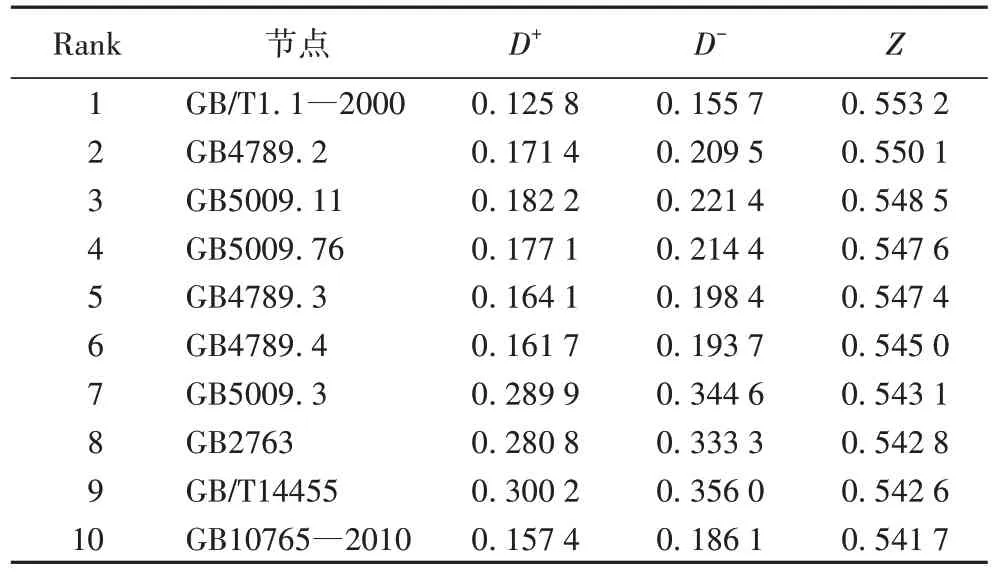

表7 标准引用网络节点综合重要性（Top10）Tab 7 Comprehensive importance of standard reference network nodes（Top10）

从表7 可以看出，最后经过综合评价后得到的排名前十的节点与之前单一属性评价时有了很大变化，其中只有GB5009.3、GB2763 和GB/T14455 在之前排名信息中出现过，而其余节点则是未曾出现过的新节点。这一情况表明，节点的度在综合评价中虽然占据较大权重，但不再是节点重要性的决定性因素，节点其他属性也起到了综合性评价作用。

5 算法评价

在节点的单一属性指标中，节点的度对节点的重要性起着重要作用，而经过综合评价后可以看到新的重要性排名与节点的度指标排名有些不同，为了验证哪种评价方式在引用网络中更为合理，本文从原始网络中分别删除两份排名表中的节点，通过比较删除节点后的网络连通性来判断节点的重要程度，因为节点集在网络中的重要性等价于在该网络中将节点集删除后对网络的破坏性，该评价方法的研究的是节点集删除前后图的连通状况的变化情况，连通性越差说明节点集对网络越重要。

表8 中展示了原始网络以及删除相应节点后的网络信息。从表8 可以看到，由于G2 和G3 中删除了相应节点后节点数目有所下降，但两者差距不大，G2 只少一个节点，但G2比G3 边的数目却少了将近700 条，只留下G1 原始图边数的52%，而G3 是77.7%，从这一点上来说，应该是G2 的连通性要更差一些。

表8 网络结构对比Tab 8 Comparison of network structure

为了对G2 和G3 有一个直观的认识，本文使用Gephi 绘图工具绘制出了这两个引用网络的图，如图3 所示。从图3可以看到，相较于原始网络G1（图1），G2 中少了很多大字体的标签节点，说明度很大的节点去掉了，而G3 与G1 的图标签节点效果差距不大，但是并不能因此而断定G2 的连通性要比G3 的连通性更差，因为整个网络的连通性并不是完全由网络中边的数量决定的。对网络中的节点进行社区划分，通过社区分类可以很好地判断整个引用网络的连通性。本文采用的社区划分算法是Louvain 算法，基本思想是：

图3 G2与G3引用网络对比Fig.3 G2 and G3 reference network comparison

1）将每个节点看作独立社区，并计算当前的模块度

Q

；2）随机选择一个节点加入其邻近社区并计算对应

Q

值，选择令

Q

值增加值最大的社区加入；3）将新的社区看作一个节点，重复上述步骤直到所有社区

Q

值不再变化。该算法进行社区划分时，由于要判断一个节点加入邻近社区的

Q

值，所以对于那些离散的节点是不进行社区划分的，因为它们没有邻近社区。因此，可以通过判断网络经过Louvain 算法社区划分后。得到的社区数量、社区内节点的数量以及未参与划分的节点数量来综合判断网络的连通性。网络的连通性越高，则划分后的社区数量越少，社区内节点数量越多，且未参与划分的节点数量越少。本文对G1、G2、G3 进行社区划分后的结果如表9 所示。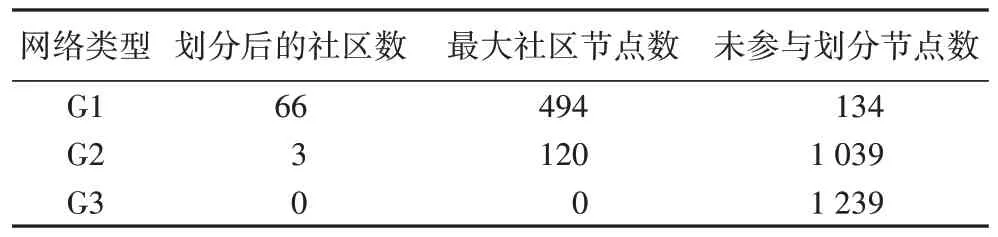

表9 网络社区划分结果Tab 9 Results of network community division

从表9 中可以看出，删除原始网络G1 中那些度数较大的节点后，整个网络G2 的连通性下降，导致离散节点增多，未参与划分的节点数量也随之增加，所以得到的社区数量也由66 个下降成3 个，最大社区内的节点数量只有原始网络划分后的最大社区节点数量的24.3%；但G3 的连通性相较于G2 要更差，整个网络中参与社区划分的节点数为0，表明这些节点之间离散程度更高，即使有一些度数较大的节点存在，但是由于缺少了一些关键节点导致它们之间无法连通，在计算模块度

Q

时不能使得

Q

值增加，无法加入任何一个社区。上述实验结果表明，使用TOPSIS 算法找出的节点要比单独使用节点的度这一单一指标效果要好，将该方法应用在食品安全标准网络中判断节点的重要性是有效的。

6 结语

为了找出食品安全国家标准中那些“重要标准”，本文挖掘了所有标准之间的相互引用关系，构建了食品标准引用网络，并分析这个复杂网络中每个节点在网络中的重要程度。本文使用的衡量指标有：节点度数、节点紧密度、节点介数以及PageRank 重要度。由于单一指标的计算不能全面地衡量节点的重要性，所以本文采用了一种节点重要性综合性评价方法，即先使用层次分析法计算各个指标参与评价的权重，再基于TOPSIS 的多属性决策方法重新计算节点重要性。

相较于仅通过度来计算节点重要性，本文方法在节点重要性判断上有了一些不一样的结果。为了比较两种结果的有效性，本文通过在网络结构中删除重要节点的方法来比较删除重要节点后网络结构的连通性，连通性的判断则是通过使用Louvain 算法对标准引用网络进行节点社区发现，网络中如果未参与社区划分的节点数量越多，该网络的连通性越差。实验结果证明，基于多属性的综合评价方法发现的重要节点被删除后，不能划入社区的节点为1 239 个，即没有任何节点被划入社区，而基于度的评价方法发现的重要节点被删除后，不能划入社区的节点为1 039 个，共发现了3 个社区，最大的社区有120 个节点，所以基于多属性的综合评价方法发现的节点在网络中更为重要。

本文的实验结果证明了多属性综合评价方法在复杂网络重要节点发现上是有效的；但在利用层次分析法计算多指标权重时，需要对比较矩阵中各指标之间的重要性关系进行人工定义，而定义的准确性依赖于操作人员的经验。为了进一步降低多属性评价方法对人的经验依赖，在未来的工作中，将考虑加入对历史评价数据的学习，以此来实现多指标比较矩阵的自动生成，增强多属性综合评价方法的智能性。