融合K-shell和标签熵的重叠社区发现算法

陈 晶，刘江川，魏娜娜*

（1.燕山大学信息科学与工程学院，河北秦皇岛 066004；2.河北省计算机虚拟技术与系统集成重点实验室（燕山大学），河北秦皇岛 066004；3.河北省软件工程重点实验室（燕山大学），河北秦皇岛 066004）

0 引言

随着对复杂网络社区发现算法的深入研究，社区发现算法为信息推荐、信息传播、精准营销等方面的应用提供了基础。社区发现算法分为静态算法和动态算法，其中静态算法包括重叠社区发现和非重叠社区发现两类。与非重叠社区发现相比，重叠社区发现更符合现实复杂网络，但存在着时间复杂度和空间复杂度较高的问题。为此，如何降低社区发现算法的时间复杂度并提高社区发现结果的稳定性研究已逐步引起了诸多学者的关注。为此，本文提出了一种基于标签传播思想的重叠社区发现算法OCKELP（Overlapping Community detection algorithm combining

K

-shell and label Entropy in Label Propagation），该算法融合了

K

-shell 和标签熵的特性，具有较低的时间复杂度和稳定的社区发现结果。本文的主要工作如下：1）提出了针对核心层节点赋标签的思想。该思想基于

K

-shell 算法对网络进行初始化处理，并针对网络中

k

值最高的节点赋予标签。通过对核心层节点赋予标签的过程，可以将网络进行初步的划分，减少网络初始化时间。

2）对网络中所有节点计算其标签熵，并按照标签熵的升序异步进行标签传播，增强了标签传播时的稳定性。

3）针对标签传播过程，引入了综合影响力，考虑节点间局部关系和节点所属的全局关系，提高了标签传播结果的准确性。

1 相关工作

针对大规模复杂网络进行社区发现有助于分析群体特征，因此，许多学者从不同的角度对社区发现问题展开了研究。社区发现的概念由Newman 等提出，将社区结构定义为社区内部节点连接紧密，社区间节点连接稀疏。由于复杂网络的规模巨大，为了简化和分析网络结构，将图论引入复杂网络。把社交网络个体以及个体间的关系抽象为图中的节点和边。2002 年，Girvan 等提出了基于图分割的GN（Girvan-Newman）算法，该算法提出了边介数的概念，对网络中所有的边计算其边介数，并依次删除边介数最高的边，直到社区不可分割。杨立文提出了一种改进的GN 算法，采用粗粒度与细粒度并行的方法计算边介数。Whites 等使用谱技术将组合图划分问题简化为几何向量空间划分问题，利用拉普拉斯矩阵得到特征向量，对特征向量进行聚类使得

Q

值最大化，从而得到社区划分。Yang 等提出了基于层次聚类的JGN（the improved Jaccard similarity coefficient in GN）算法，通过对所有节点计算改进的Jaccard 相似系数，并删除拥有最小相似系数的节点间的连边而得到社区结构。

标签传播算法是一种半监督学习方法，由Zhu 等提出。随后，Raghavan 等提出了RAK（Raghavan Albert Kumara）算法，将其应用到非重叠社区发现中，该算法具有线性时间复杂度，但RAK 算法的随机性较强、鲁棒性较弱。Sun 等提出了CenLP（Centrality-based Label Propagation）算法，该算法通过计算每个节点的局部密度和高密度邻居的相似度，改进了节点更新顺序和相似关系。Xie 等提出了LabelRank 算法，该算法通过引入4 个算子使得LPA（Label Propagation Algorithm）的稳定性得到了提升。Blondel 等提出了Louvain 算法，该算法使用模块度优化的方式为节点划分社区。薛青提出了一种基于修剪策略的改进Louvain 算法PRULOU（improvement of louvain algorithm based on pruning in complex networks），该算法利用修剪策略消除了Louvain 算法中的社区划分震荡和模块度震荡问题。Waltman 等提出了SLM（Smart Local Moving）算法，通过分割社区，将节点集从一个社区移动到另一个社区，不断搜索模块度增益的可能性，从而进行大规模网络社区发现。

重叠社区发现CPM（Clique Percolation Method）由Palla等提出，其核心是通过寻找极大完全子图进行重叠社区发现。Gregory在RAK 算法的基础上提出了重叠社区发现算法（Community Overlap PRopagation Algorithm，COPRA），该算法通过引入参数

v

，使得每个节点最多可以隶属于

v

个社区。Wu等提出了平衡多标签传播算法（Balanced Multi-Label Propagation Algorithm，BMLPA），引入了平衡归属系数，使得节点理论上可以属于无限个社区。沈海燕等在COPRA 的基础上借鉴了CPM 算法的极大子团方式将标签初始化过程的时间缩减，并在标签传播过程中引入了影响力因素减少了算法的随机性。邓琨等提出了一种基于多核心标签传播的重叠社区识别（Overlapping community detection in complex networks based on Multi Kernel Label Propagation，OMKLP）方法，采用多个核心节点的方式进行标签传播。由于不需要预先设置参数，增强了算法的稳定性。Lu 等提出了LPANNI（Label Propagation Algorithm with Neighbor Node Influence），该算法加入了邻居节点影响力，并按照节点重要性升序更新节点标签。Cheng 等提出了基于局部扩展的局部邻域信息重叠社区识别算法（local-expansion-based Overlapping-Community detection algorithm using Local-Neighborhood information，OCLN）来大规模复杂网络，该算法在社区扩展时仅考虑了社区中的关键邻居。Shi 等提出了COLBN（overlapping community discovery algorithm based on label propagation），根据参考节点划分初始社区，选择重叠节点中的参考节点划分重叠社区。Tang 等在SLPA（Speakerlistener Label Propagation Algorithm）的基础上提出了基于局部和全局属性衡量节点影响的度量方法，通过删除

k

个影响力最小的重叠节点来识别重叠社区。

2 本文算法

2.1 相关技术

COPRA 定义了一个参数

v

，规定社区内节点最多隶属于

v

个社区，并为每个节点在初始时刻定义一组标签(

c

，

b

)。其中，

b

是归属系数，

c

为社区标签，每个节点可以拥有多组标签，并且该节点所拥有的所有标签的归属系数和为1，归属系数定义如式（1）所示：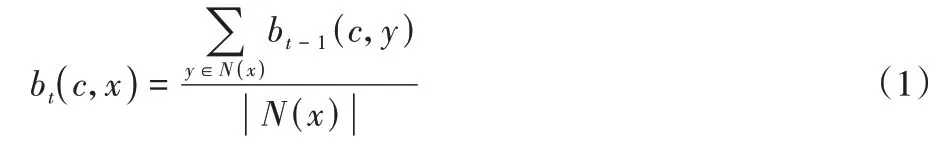

其中：

b

(

c

，

y

)表示上一次迭代后

x

节点的邻居节点的标签信息；

N

(

x

)为节点

x

的邻居节点集。

K

-shell 算法是由Kitsak 等提出的

k

核分解法，其核心思想是对复杂网络进行粗粒度划分，从而找出重要性高的节点。该算法的前提条件是默认图中至少存在度为1 的节点。经过

k

核分解后，对应度为

k

时被删除的节点记为

K

-shell。该算法将网络进行了层次划分，从全局来看，把网络划分为1-shell 层到

K

max-shell 层，其中1-shell 层为影响力最小的节点集，

K

max-shell 层为网络中影响力最大的节点集。

为了解决标签传播算法稳定性差的问题，Zhao 等基于信息论提出了标签熵的概念，并将标签传播顺序按照标签熵从小到大的顺序传播，提高了算法的稳定性。标签熵的定义如式（2）所示：

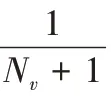
2.2 标签初始化阶段

重叠社区发现算法的初始化过程大多是对网络中所有节点进行赋予标签操作，随着网络规模的增加，运行时间会迅速增长。因此，本文提出的OCKELP 采用了针对网络进行

K

-shell 分解处理，得到核心层节点的预处理方式。其中，核心层节点的定义如式（3）所示：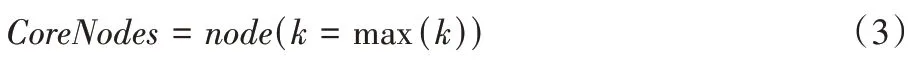

其中：

CoreNodes

表示核心层节点，

node

(

k

=max(

k

))表示取

k

值最大的节点作为核心层节点。在大多数网络中，大部分节点属于影响力较小的节点，而少数节点是影响力较大的节点，利用

K

-shell 算法得到的核心层节点具有较大的影响力。对核心层节点赋予标签，经过少数几次迭代后，就可获得社区划分的初始结果和较高的时间效率。

2.3 标签更新顺序

标签传播重叠社区发现算法在标签更新时采取的是随机更新策略，其结果会导致社区发现结果的随机性大。相关研究表明，标签在节点中更新顺序会极大影响结果的随机性，所以本文引入了标签熵，来解决标签传播算法稳定性差的问题。

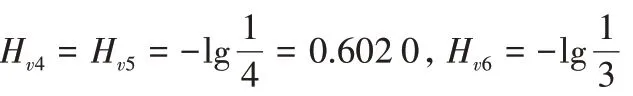
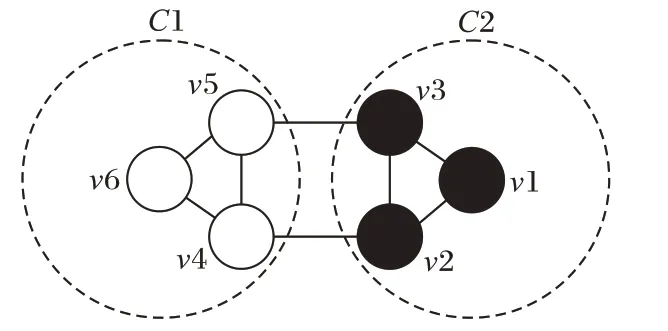
图1 两个社区的强关联社区图Fig.1 Strongly connected community graph of two communities

此外，为了避免标签震荡，本文算法采用异步更新规则。即

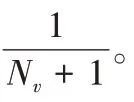
t

时刻节点

v

更新时与

t

时刻未更新的邻居节点标签和

t

时刻已更新的邻居节点标签有关，如式（4）所示：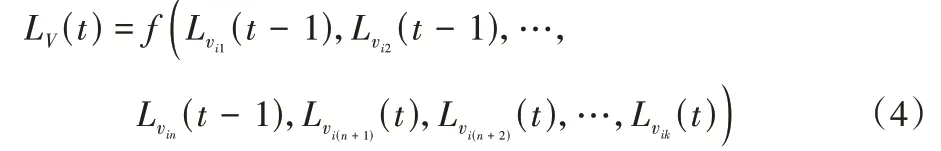

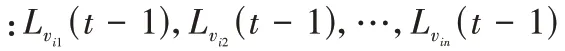
2.4 标签选择过程

大多数标签传播算法在进行标签选择时，未考虑节点间的相似度和节点在网络中的影响力，为此，本文融合Jaccard相似度和

K

-shell 算法的

k

值，综合考虑节点间的相似度和节点所属社区层次的影响，将其加入标签更新中，使得在进行标签选择时，考虑了节点间相似性和节点本身的影响力，降低了随机性，提高了社区发现结果的稳定性和准确性。将Jaccard 相似度以及层次信息

k

值融合为综合影响力，如式（5）所示：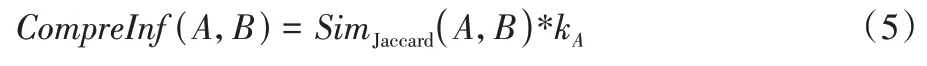

利用

k

值作为系数去放大节点间的相似度，将节点的层次信息与局部信息融合，构成综合影响力

CompreInf

，将

CompreInf

值引入到标签更新中，如式（6）所示：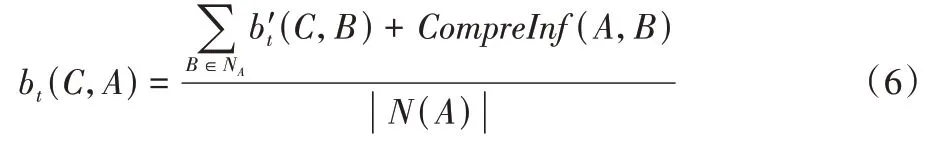

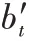
需要注意的是，当标签更新选择结束后，还需要对节点所拥有的从属系数集进行归一化，如式（7）所示：

其中：

C

表示

A

节点所拥有的社区标签集合。

3 OCKELP实现

3.1 算法基本步骤

OCKELP 的具体步骤如下：

步骤1 对网络进行初始化，利用

K

-shell 算法得到

k

值最高的节点集，赋予这些节点不同的标签对(

c

，1)，其中1 为初始从属系数。

步骤2 初始化各个节点的标签熵，并按升序排序。

步骤3 采用异步更新的方式，根据式（5）计算出节点间的综合影响力，根据式（6）得到节点所含有的标签的从属系数，并利用式（7）进行归一化。对节点计算其标签熵，删除从属系数小于1/

v

的标签。如果该节点所有标签的从属系数均小于1/

v

，则选择从属系数最大的标签，当出现最大值有多个时，执行步骤4，再利用式（7）进行归一化。

步骤4 从多个候选标签中选择一个作为该节点的标签。

步骤5 算法满足终止条件时结束，并将标签相同的节点合并成一个社区；否则，继续执行步骤3 和步骤4。

3.2 算法伪代码

OCKELP 由网络初始化和标签传播两部分组成，算法伪代码如下：

算法1 网络初始化算法。

输入 社区网络图

G

（

V，E

）。输出 初始化后的社区网络图

init_G

（

V，E

），部分节点具有标签。

根据算法1 可知，首先遍历网络中的节点并求出相应的度值，其次根据

K

-shell 算法，得到每个节点对应的

k

值，找出拥有最大

k

值的节点即核心层节点赋予其标签。由于仅对核心层节点赋予标签，可以降低对所有节点赋予标签的时间，提高了标签传播阶段的效率。

第二部分是标签传播，基于算法1 对初始化后的社区进行标签传播，伪代码描述如下所示。

算法2 标签传播。

输入 初始化后的社区网络图

init_G

（

V，E

），参数

v

。输出 社区信息

communities

。

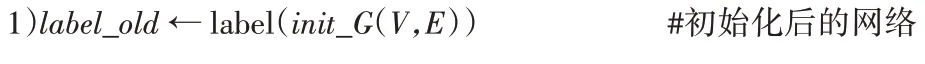
3.3 算法时间复杂度分析

假设

n

代表节点数，

m

为边数，

v

表示节点最多可以隶属的社区个数。初始化算法主要是由

K

-shell 算法以及遍历网络节点找出拥有最大

k

值的节点赋予标签组成。初始化算法第2）～6）行以及第8）～12）行都对网络中

n

个节点进行了遍历，这两部分的时间复杂度都为

O

(

n

)，所以初始化算法整体的时间复杂度也为

O

(

n

)。

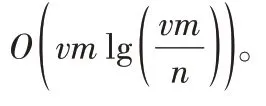
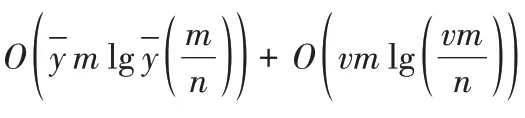
4 实验与结果分析

4.1 评价指标

在真实网络数据集上，实验采用重叠社区模块度EQ（ExtendQ）作为评价指标；在人工网络数据集上，采取重叠社区归一化互信息（Normalized Mutual Information，NMI）值作为评价指标。

1）重叠模块度EQ。

Nicosia 等和Shen 等分别提出了重叠社区模块度Qov 和EQ，EQ 描述如式（8）所示：

其中：

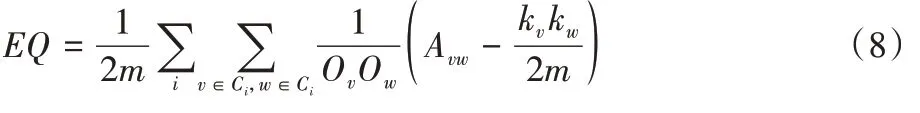
m

为社区中的总边数；

O

、

O

分别代表节点

v

和节点

w

属于的社区数量；

k

、

k

分别代表节点

v

和节点

w

的度。当每个节点最多只属于一个社区时，

EQ

等价于

Q

，当所有节点都属于同一个社区时，

EQ

=0。

2）重叠社区的归一化互信息NMI。

为了检测重叠社区发现结果的质量，Lancichinetti 等提出了识别重叠社区发现与真实社区匹配程度的指标NMI，如式（9）所示：

其中：

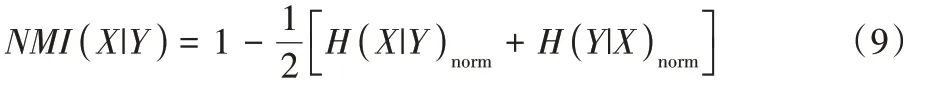
X

代表真实社区；

Y

代表经过社区发现算法后的社区；

H

(

X

|

Y

)为归一化条件熵。

McDaid 等认为Lancichinetti 等提出的NMI 在极端情况下表现不理想，因此对NMI 定义进行了改进，定义如式（10）所示：

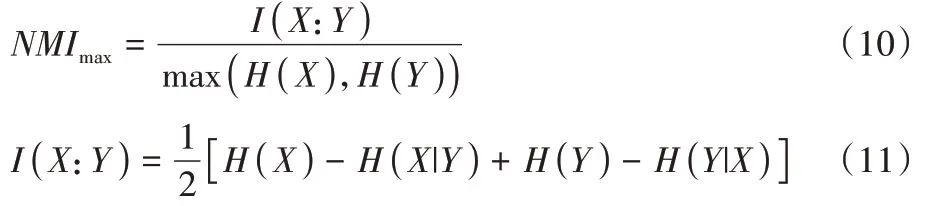
4.2 实验数据集

真实网络数据集来源于斯坦福大学的大型网络数据集和Newman 教授的个人数据网站。表1 展示出真实网络数据集的相关信息。举例说明：Karate 数据集提供了TXT 文档和GML 文档，其中TXT 文档提供节点集和边集；GML 文档可利用gephi 将数据集可视化，展示出真实社区划分的结果。

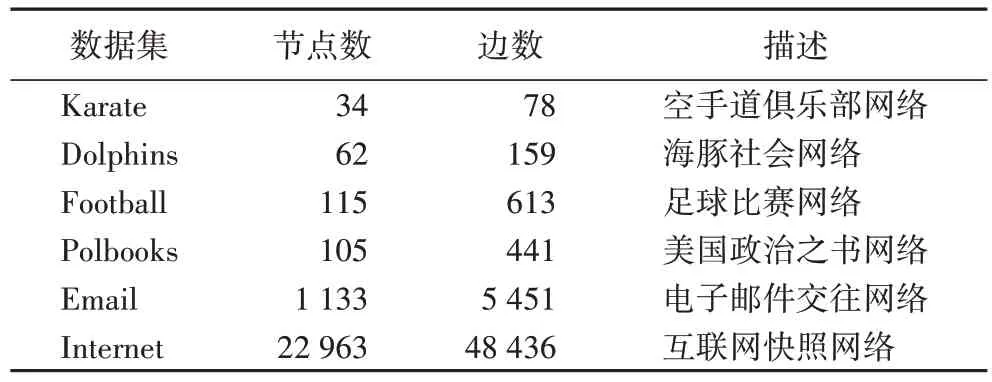
表1 真实网络数据集Tab 1 Real network datasets

Lancichinetti 等提出了LFR 基准网络，由于该基准网络与现实网络极为相似，并且具有真实的社区划分结构，因此，本文采用LFR基准网络作为人工网络数据集对OCKELP 进行实验验证。LFR基准网络的基本参数描述如表2所示。

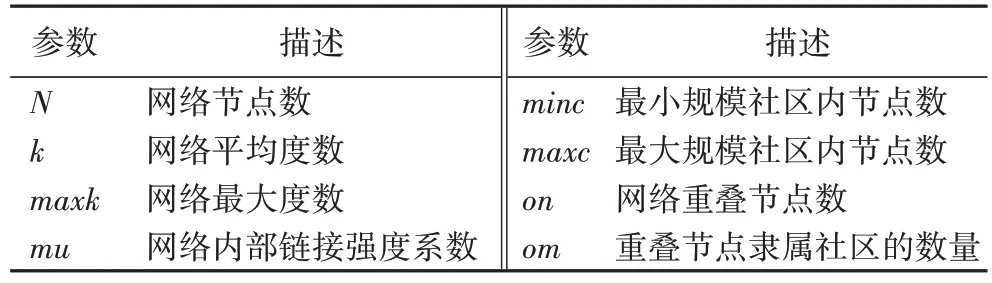
表2 LFR基准网络参数描述Tab 2 LFR benchmark network parameter description

利用LFR 生成了4 个人工网络数据集进行实验对比，4个人工网络数据集具体参数如表3 所示。

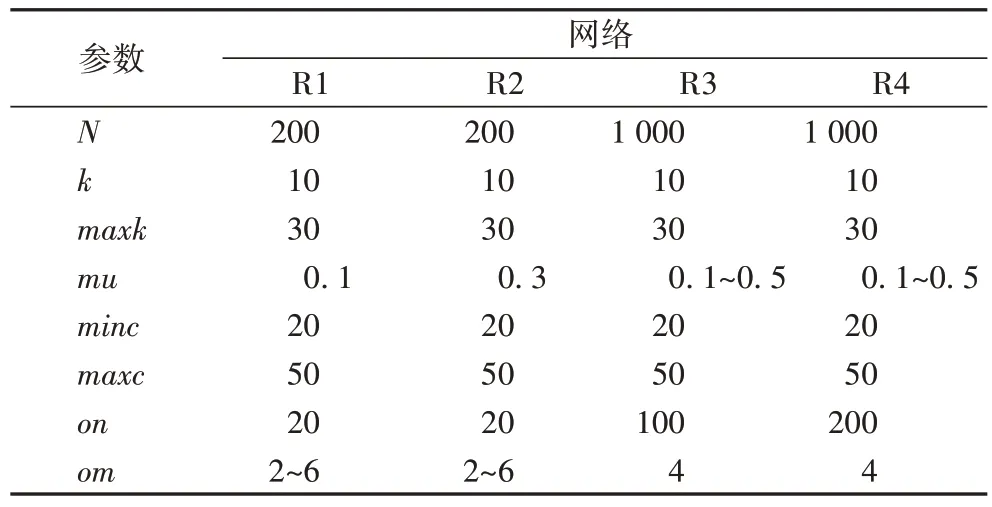
表3 四个LFR基准网络参数Tab 3 Four LFR benchmark network parameters

4.3 实验结果分析

在真实网络数据集上，将所提出的OCKELP 算法与COPRA、OMKLP、SLPA、MNMF（Modularized Nonnegative Matrix Factorization）、NNSED（Non-Negative Symmetric Encoder-Decoder）进 行 对 比。由 于COPRA 和SLPA 稳定性不好，所以本实验分别取COPRA、SLPA 运行20次结果的平均值。

Karate 数据集是空手道俱乐部网络，含有34 个节点和78条边，该空手道俱乐部真实社区分布，如表4 所示。

表4 Karate数据集网络真实划分Tab 4 Real partition of Karate dataset network

从表4 和图2 可以发现，OCKELP 在Karate 上的实验结果除了节点10 归属，其他节点归属都与Karate 网络真实划分一致。节点10 被划分到了两个社区中，其原因是节点10 在两个社区的联系都较为紧密，不容易确定其归属社区。

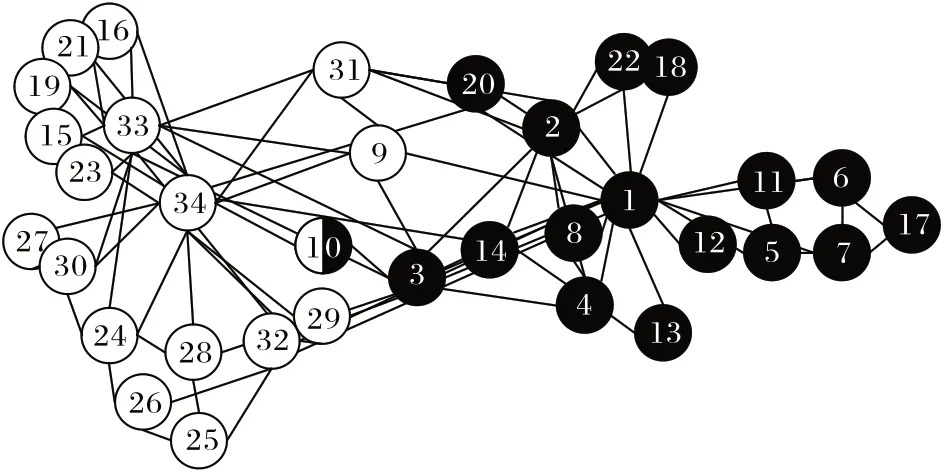
图2 Karate网络实验结果Fig.2 Results of Karate network experiment

采用真实网络对EQ 值进行验证，结果如表5 所示。从表5 可知，OCKELP 在Karate、Polbooks、Internet 数据集上，EQ值都优于其他算法；在Dolphins 网络中仅次于OMKLP 算法，并且相差很小；在Football 网络和Email 网络中EQ 值仅次于MNMF 算法。原因是：由于数据集规模较小，存在一些联系过于密切的节点，导致标签选择时，影响力因素的作用被削弱。在规模较大的网络中，OCKELP 表现最优，说明了OCKELP 在标签选择时，通过增加影响力因素可以提高社区发现结果的准确性。综上所述，OCKELP 在大多数真实网络数据集中能够获得准确的社区划分结果，获得更高的EQ 值。

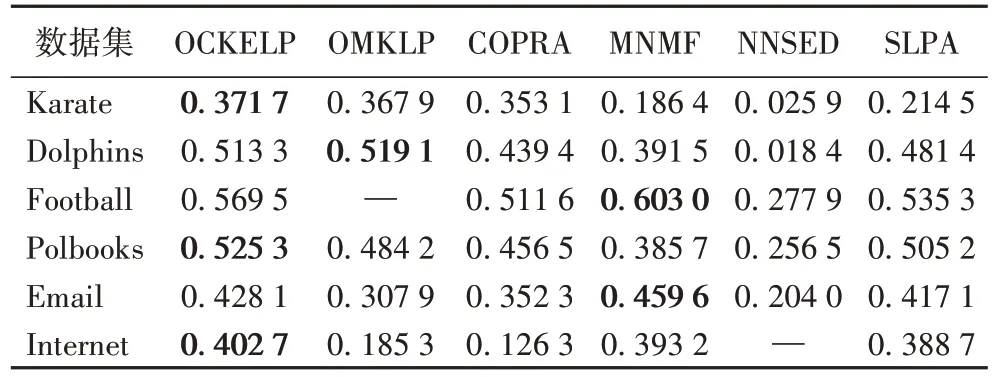
表5 不同算法的EQ值比较结果Tab 5 Comparison results of EQ values of different algorithms

在人工网络数据集中，由于MNMF、NNSED算法无法识别非连通图，所以OCKELP仅与COPRA、OMKLP、SLPA进行比较。

在R1 网络中，验证了重叠节点隶属社区的数量对NMI值的影响。此时

mu

值为0.1，R1 网络的社区结构比较清晰。如图3 所示，OMKLP 算法表现整体较为平稳，

om

的增加对于其影响不大，但其他算法的识别准确度要低于本文算法OCKELP。SLPA 初始时NMI 值较高，但随着

om

的增加，NMI下降趋势较为明显，稳定性较差。COPRA 的识别准确度较低，稳定性一般。本文算法OCKELP 除了在

om

=4 时NMI 值略低于OMKLP 算法之外，在其他

om

取值中都有着较好的结果。虽然随着

om

值的增大，出现了NMI 值下降的情况，但总体趋势平稳，没有出现由于重叠节点所隶属社区数的增多而导致NMI 值快速下降的情况。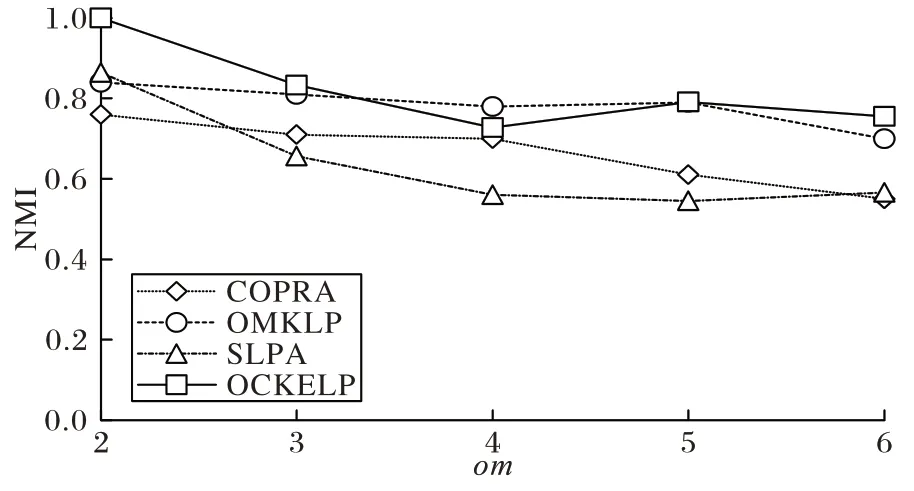

图3 R1网络中的NMI值（mu=0.1）Fig.3 NMI values in R1 network（mu=0.1）

R2 网络除了

mu

值改变外，其余参数不变。

mu

值为0.3，由于

mu

值增加使得R2 网络的社区结构变得较为模糊，所以在R2 网络的实验中，社区发现结果的NMI 值整体呈现下降趋势，如图4 所示。OMKLP、COPRA 随着

om

值的增加，NMI 值逐渐降低，而SLPA 识别准确度一直较低。OCKELP的识别准确度最优，且随着

om

值的增加，NMI 值变化不大，保持着较为平稳的趋势。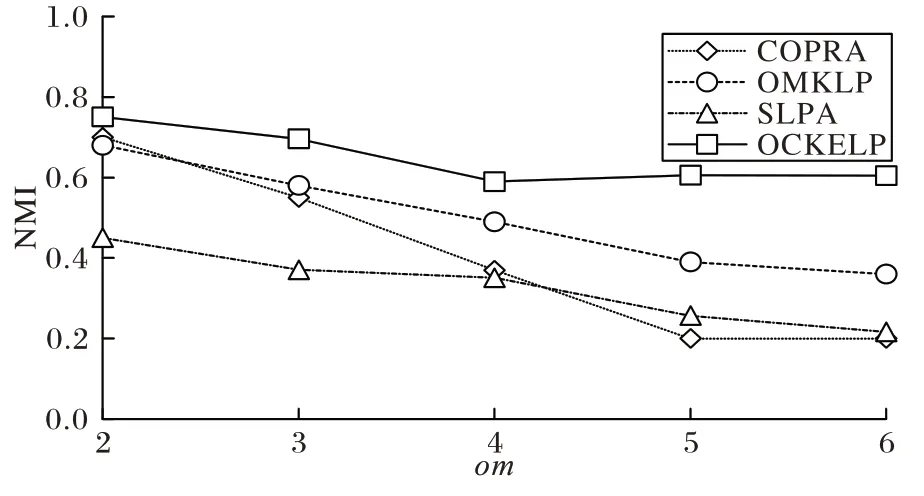

图4 R2网络中的NMI值（mu=0.3）Fig.4 NMI values in R2 network（mu=0.3）

在R3 网络中，主要验证了

mu

值对NMI 值的影响。

mu

值是体现社区结构清晰程度的参数，随着

mu

值的增加，社区结构逐渐弱化，意味着边缘节点和社区内部节点的标签熵影响力变强。如图5 所示，OMKLP、COPRA、SLPA 在

mu

=0.1 时得到的NMI 值都比较高，但随着社区结构逐渐模糊，NMI 值下降速率很快，尤其是COPRA、SLPA，在

mu

=0.5 时，几乎观察不到社区结构，算法的稳定性较差。OCKELP 的NMI 值要优于其他三个算法，虽然随着

mu

值增加有所下降，但是下降速率很慢，说明OCKELP 具有良好的稳定性，可有效识别模糊社区结构。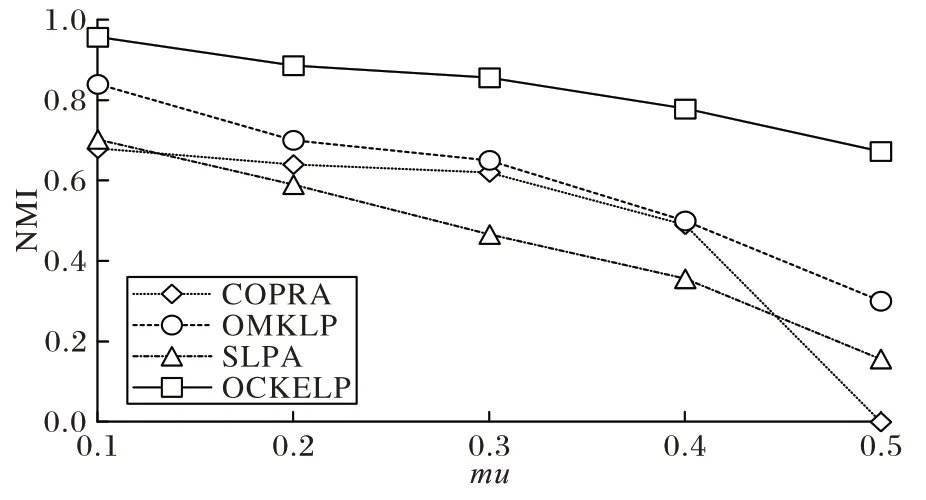

图5 R3网络中的NMI值（on=100）Fig.5 NMI values in R3 network（on=100）

在R4 网络中，除了重叠节点数量从100 变为200 以外，其他参数与R3 网络保持一致，其原因是为了验证重叠节点数量对社区发现结果的影响。如图6 所示，对比R3 网络，所有算法都受到了

on

的影响，NMI 值整体上呈现降低的趋势，说明了重叠节点数量的增加会影响重叠社区发现的质量。SLPA、COPRA 在

on

=200，

mu

=0.5 时已无法挖掘出社区的有效信息。

on

对OMKLP 算法影响不大，与R3 网络中整体趋势相近。OCKELP 在不同的

mu

值下相较于其他三个算法具有最优的NMI 值，

on

对OCKELP 的影响不明显，整体趋势较为平稳。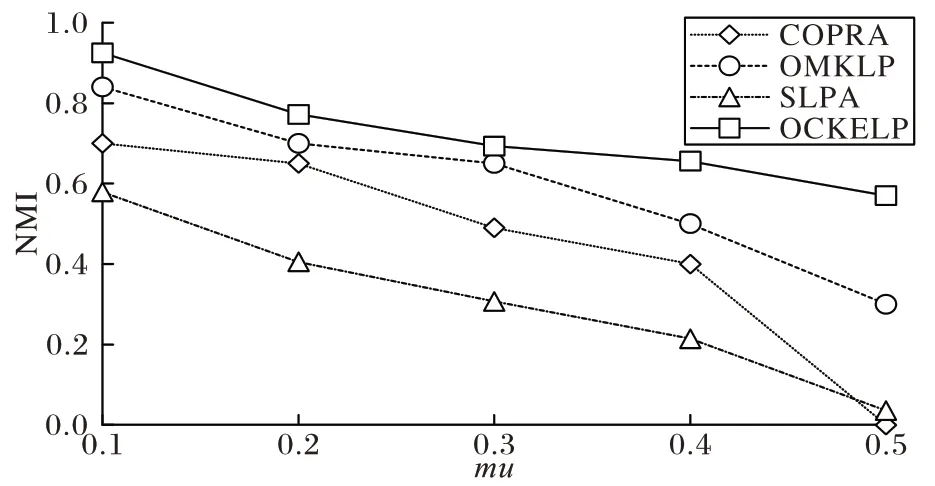

图6 R4网络中的NMI值（on=200）Fig.6 NMI values in R4 network（on=200）

综上可知，在真实网络数据集中，OCKELP 在大多数网络中重叠社区发现结果的EQ 值最优。在人工合成数据集中，

om

与

on

的增加对OCKLEP 算法影响不大。随着

mu

值的增加，OCKELP 的NMI 值呈现了下降的趋势，但相较于OMKLP、SLPA、COPRA 下降趋势不明显，其主要原因是：标签传播算法对于节点间连接紧密程度的敏感性较高，对于社区的清晰程度有着较大的依赖。实验结果表明，OCKELP 比OMKLP、SLPA、COPRA 有着更好的稳定性，在EQ 和NMI 值上，OCKELP 具有较高的社区划分质量和稳定的社区划分结果。

5 结语

本文提出了融合

K

-shell 和标签熵的标签传播重叠社区发现算法OCKELP。首先，利用

K

-shell 算法进行标签初始化，按照标签熵从小到大的顺序进行标签更新；其次，在标签选择阶段提出了综合影响力，将社区层次信息和节点局部信息融合。在真实网络数据集和人工网络数据集上进行了实验对比，实验结果证明了OCKELP 的稳定性和有效性。

在未来的工作中将会进行如下的深入研究：1）将本文算法拓展为动态社区发现算法，从而可以对动态社区进行社区发现；2）将本文算法拓展到有向有权图中。