融合节点覆盖范围和结构洞的影响力最大化算法
杨 杰,张名扬,芮晓彬,王志晓
(中国矿业大学计算机科学与技术学院,江苏徐州 221116)
0 引言
随着在线社交网络的飞速发展,越来越多的用户喜欢在社交网络上转发时事新闻并分享自己的观点,使得影响力传播问题成为社交网络分析领域中的研究热点。影响力最大化问题是从网络中选取部分节点,从而使得当这些节点在网络中扩散消息时,最终能够影响到的节点数量最大化。该问题作为病毒式营销和在线广告投放的重要依据,引起了学者们的广泛关注。
影响力最大化问题最早由Domingos 等提出,旨在寻找k
个初始种子节点,并使得最终的信息传播范围最广。后来,国内外学者从不同角度提出了多种影响力最大化算法,这些算法可大致分为两类:一类是基于蒙特卡洛模拟的贪心算法及其改进算法;另一类是基于网络拓扑结构的启发式算法。贪心算法能保证至少达到最优解63%的传播范围,但时间复杂度较高,不适用于大规模网络。启发式算法效率较高,但性能不稳定,受网络结构影响较大。在贪心算法方面,Kempe 等提出General Greedy 算法,该算法有着很高的精确度,但在每次选取种子节点时需要遍历整个网络并执行数千次的蒙特卡洛模拟过程,导致该算法效率较低。优化后的贪心算法CELF(Cost-Effective Lazy Forward selection)利用函数的子模性对运行效率进行了改进,运行效率比之前提高了约700 倍。之后,Chen 等又提出了New Greedy 算法和Mix Greedy 算法来优化贪心算法,然而,优化后的贪心算法运行时间仍然较高,很难应用到大规模网络中。
近年来,研究者倾向于设计启发式算法来解决贪心算法运行效率低的问题。Chen 等提出的DegreeDiscount 算法是经典的启发式算法,该算法通过削弱邻居节点度值来避免所选种子过于集中,提高了最终性能。Nguyen 等提出pBmH(probability-Based multi-Hop diffusion)算法,该算法将节点在多跳邻域内能影响的节点数作为中心性指标,确保筛选出的种子节点不相邻。高菊远等和Wang 等将节点的覆盖范围增益作为衡量节点影响力的中心性指标,进一步避免了“富人俱乐部”现象,提出的基于节点覆盖范围的算法(Node Coverage Algorithm,NCA)性能表现突出。但是,该算法仅依靠单一的中心性指标来衡量节点影响力,只能反映节点的单一属性,无法很好地适应网络结构的变化,因此在不同结构特征的网络中表现不稳定。
本文从多属性融合的角度提出一种基于覆盖范围和结构洞的影响力最大化算法(influence maximization algorithm based on Node Coverage and Structural Hole,NCSH),该算法融合节点的覆盖范围和结构洞性质对节点影响力进行全面评价,有效解决了传统基于拓扑结构的启发式算法性能不稳定的问题。实验结果表明相较于其他算法,本文所提算法能够获得更大的节点影响范围,并且,随着网络规模及结构的变化,本文算法表现出良好的稳定性。
1 节点覆盖范围计算
节点的覆盖范围是指节点本身及其能直接影响到的一阶邻居节点数量,若这些节点中存在其他种子的邻居节点,则去除这些重复节点后的数量即为节点的覆盖范围增益。一组节点的覆盖范围为它们各自覆盖范围的并集。例如,用N
表示节点i
的邻居集合,则节点i
和节点j
的共同覆盖范围N
∪为:
S
的覆盖范围N
如式(2)所示: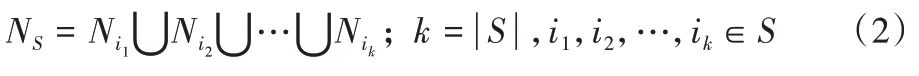
v
的覆盖增益计算方法如式(3)所示: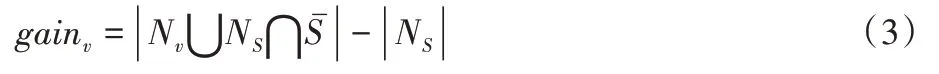
N
为节点v
的邻居集合;N
为种子集合S
的节点覆盖范围;S
ˉ为网络中不包含种子的节点集合。由于大部分社交网络传播概率较低,所能影响到的节点集中在其一阶邻居,因而选取节点覆盖的一阶邻居数量作为覆盖范围增益,忽略与现有种子集的重叠邻居,着重考察非重叠邻居数量,可有效避免“富人俱乐部”现象,进一步提高影响范围。
2 节点结构洞特性评价
对于社交网络中不直接相连的两节点之间,若能通过某个中间节点实现间接连接,则将该中间节点称之为具有结构洞性质的节点。结构洞性质能够表示信息在网络中完全扩散的必经之路,不同于介数中心性,它仅通过邻域的拓扑关系便可计算得到,时间复杂度较低。结构洞节点能够有效控制信息流向邻居节点,从而具有更高的网络覆盖范围收益。如图1 所示,节点2 是三个社区之间的结构洞,若移除该节点,则信息无法在社区间相互传输。Lou 等发现Twitter上1%的结构洞节点决定着25%的信息流向,因此结构洞节点的加入可以扩大信息的扩散范围。此外,结构洞特性对于社交网络中的社区发现问题也具有重要意义。
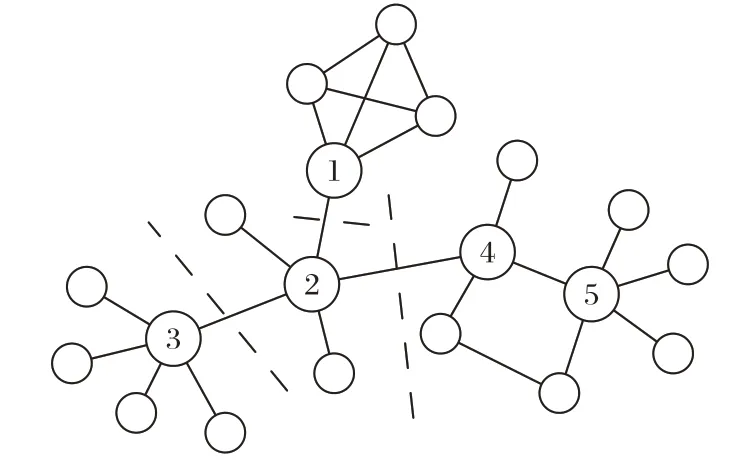
图1 节点结构洞特性Fig.1 Node structure hole characteristics
苏晓萍等指出可以用网格约束系数来衡量网络节点在形成结构洞时受到的约束:
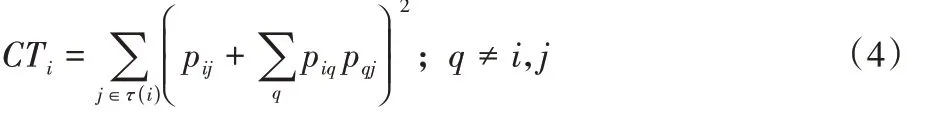
CT
为节点i
的约束系数;τ
(i
)为节点i
的邻居节点;节点q
为节点i
和节点j
的共同邻居;p
表示节点i
连接节点j
付出精力的比重。p
的计算公式如下:
其中:

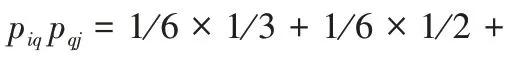
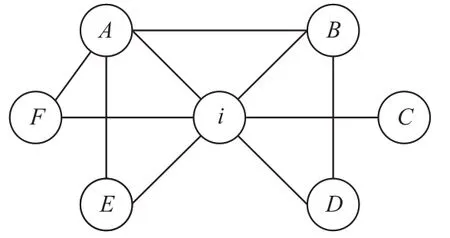
图2 约束系数计算Fig.2 Constraint coefficient calculating
网格约束系数能考量节点的度值和邻域连接紧密度,若节点的约束系数越小,则意味着其具有较高的度值和较低的邻域链接紧密度,使得该节点具有程度更高的结构洞性质。在具有相同覆盖增益的情况下,该节点作为信息传播的中枢节点,有利于将信息扩散至其他社区,进一步扩大影响范围。
3 本文算法
3.1 问题定义
影响力最大化问题是在给定社交网络G
(V
,E
)中选择最具影响力的k
个节点集合S
(通常称为种子节点),使其在一定的传播模型下能影响到尽可能大的网络范围σ
(S
)。
3.2 算法描述
为解决IM 问题,本文所提NCSH,其基本思想为:首先,利用节点覆盖范围增益的中心性指标选择覆盖范围增益最大的节点;然后,随着所选种子节点数量的增加,每轮可能会出现多个覆盖增益相同的候选种子节点;在这种情况下,从候选种子集中选择约束系数最小的节点,确保具有最大的网络传播收益;最终重复此过程,直至选出k
个种子节点。算法1 基于覆盖范围和结构洞的影响力最大化算法(NCSH)。
输入 网络G
(V
,E
),种子节点数k
。输出 种子节点集合S
。

图3 为NCSH 的执行过程。首先,算法选择度值最大的节点15 作为1 号种子,其覆盖范围在图3(a)用横线标出。接着,算法更新剩余节点的覆盖范围增益(图3(b)),更新结果显示节点5 的覆盖范围增益(竖线标出节点)最大,所以选择节点5 作为2 号种子。
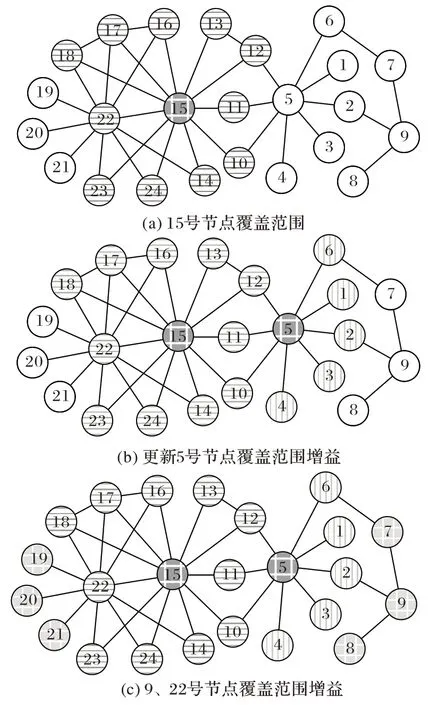
图3 NCSH执行过程Fig.3 Execution process of NCSH
然后,算法再次更新剩余节点的覆盖范围增益,更新结果显示节点22 和9 的覆盖范围增益同为最大,选择它们均可扩大3 个节点的范围(如图3(c)所示的正方形网格节点)。此时,算法根据网格约束系数判断22 号节点(约束系数为0.249 3)比9 号节点(约束系数为0.506 2)小,因此选择22 号为3 号种子。可以发现,在本图例中,与9 号节点相比,22 号节点具有较高的度值和较强的社区中心性,虽然它们的覆盖增益均为3,但22 号节点还有额外6 次机会去影响15 号节点未激活的节点,从而能够最大化影响范围。
3.3 算法复杂度
假设网络G
(V
,E
)包含n
个节点。算法每选择一个种子节点,需要更新其余所有节点的覆盖范围增益。更新一个节点覆盖范围增益的复杂度可近似为O
(d
),其中d
为节点平均度值。计算n
个节点的覆盖范围增益的时间复杂度则为O
(dn
)。由此可见,选取k
个种子节点的时间复杂度为O
(kdn
)。在选择种子节点之前需要计算n
个节点的约束系数,复杂度为O
(d
n
)。因此,NCSH 总的时间复杂度为O
(dn
(k
+d
))。4 实验与结果分析
4.1 实验设置
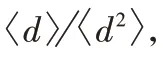
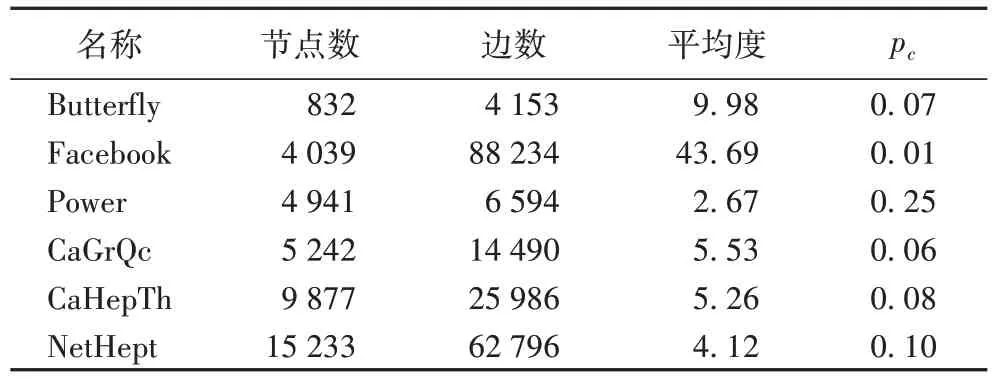
表1 实验数据集Tab 1 Datasets for experiments
4.2 实验结果与分析
在社交网络分析领域中,影响力最大化算法的评价指标通常为:
1)影响范围,即筛选并激活相同规模的种子节点集合。在相同的传播模型下该集合最终激活的节点个数越多表示影响范围越广。本文是在独立级联传播模型(Independent Cascade model,IC)下使用Monte-Carlo 模拟5 000 次传播过程并求取平均值作为影响范围。
2)运行时间,即在相同条件下选择同等规模的种子节点集合所花费的时间t
。t
越小表明算法的效率越高。本文选取以下几个典型算法进行对比分析:Degree,DegreeDiscount、pBmH、NCA、基于结构洞和度折扣的最大化算法(maximization algorithm based on Structure Hole and DegreeDiscount,SHDD)。
图4 展示了随着种子节点数由5 增大到50,六种算法在六个真实数据集中的影响范围变化情况。
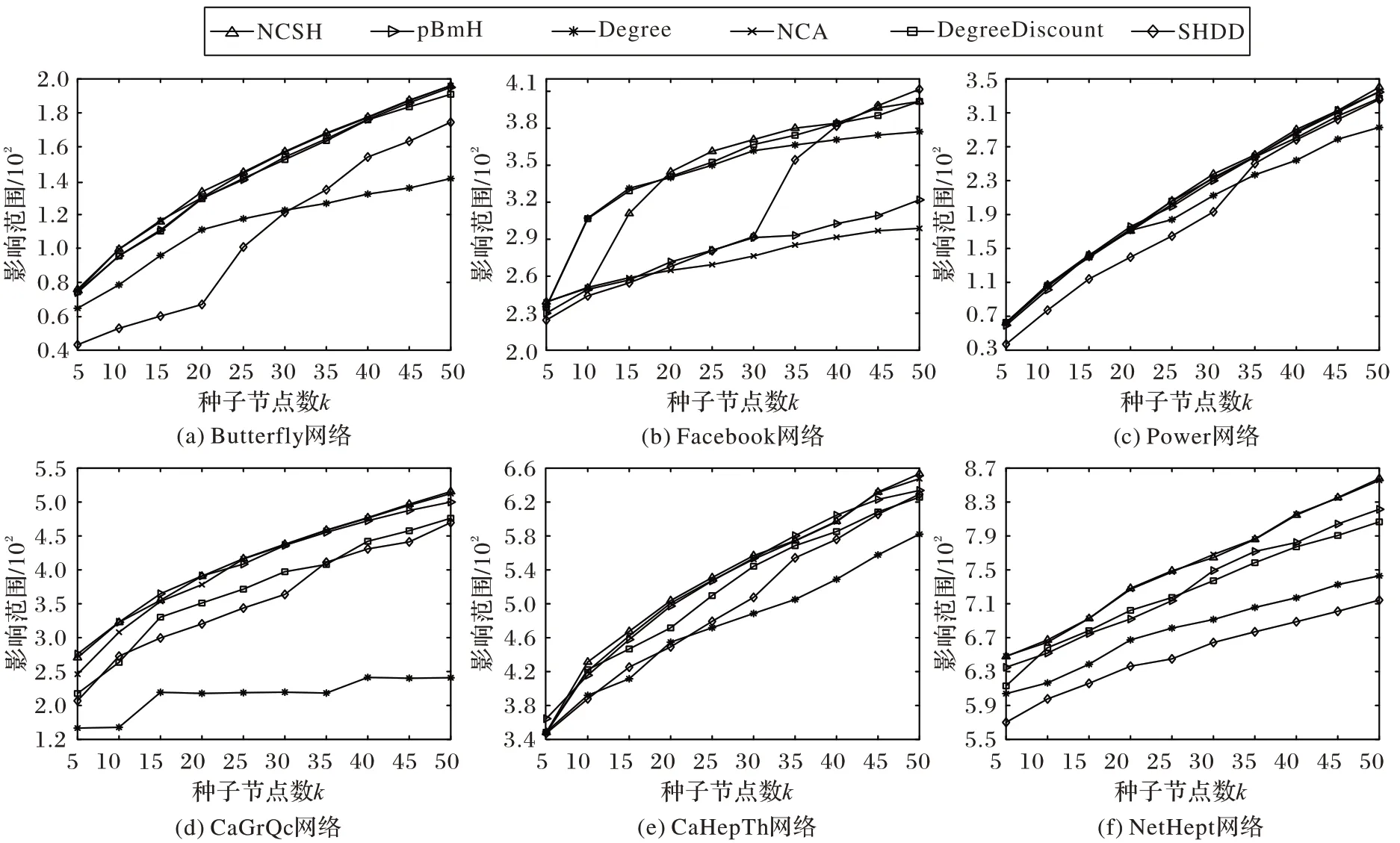
图4 不同算法在六个真实网络中的影响范围Fig.4 Influence spread of different algorithms on six real networks
1)在Butterfly 网络中,NCSH 与NCA 表现最优,Degree、SHDD 性能较差;
2)在Facebook 网络中,由于该网络为自我中心网络,其中少量节点就能覆盖到网络的全部节点,因而在k
=10 时,NCA 无法有效选取种子,pBmH 算法在该网络中也表现较差,DegreeDiscount 算法、Degree 算法和SHDD 利用了节点的中心度属性,因而具有较好表现,而NCSH 在覆盖范围属性失效后,仍能根据结构洞性质有效选取影响力大的种子节点,最终达到较大的影响范围;3)在Power 网络中,NCSH 几乎全程保持最大的影响范围,在k
为35 至50 时,其覆盖范围相较于NCA 仍有明显优势,分别提高了2.7%、1.4%、1.9%、1.5%;4)在CaGrQc 网络中,NCSH 除了在k
=5 和k
=15 时的影响范围略低于pBmH 算法,在其他情况下的影响范围均为最高,尤其在k
=5、10、20 时,相较于NCA 分别有9.8%、6.8%、4%的提升,DegreeDiscount 算法和SHDD 表现一般,Degree 算法较差;5)在CaHepTh 网络中,k
=5 时,pBmH 算法具有最高的影响范围,但随着种子数量的增加,NCSH 的优势体现出来;在k
=10 时,相较于NCA 有2.6%的提高。由此可见,在种子数量较少时,NCSH 相较于NCA 提升较大。在NetHept 网络中,NSCH 表现最优,pBmH 与DegreeDiscount 算法性能一般。
图5 展示了IC 模型下六种算法在六种不同网络下影响范围随传播概率增加的变化情况,针对不同网络选择适合它们的传播概率范围:1)Butterfly 与NetHept 网络的传播概率从0.03 增大到0.11,步长为0.01;2)Facebook 网络的传播概率从0.006 增大到0.014,步长为0.001;3)Power 网络的传播概率从0.21 增大到0.29,步长为0.01;4)CaGrQc 与CaHepTh网络的传播概率从0.01 增大到0.09,步长为0.01。从图5中可以看出,NCSH 在多个网络中能达到最大的影响范围。
在Butterfly 网络(图5(a))中,NCSH 与NCA 表现最佳。由图5(b)可以看出,在Facebook 网络中,当传播概率较小时,各种算法的影响范围相差不大,随着传播概率的增大,除了NCA 和pBmH 算法之外,其余算法均表现出较高的增长趋势,由于传播概率较小,DegreeDiscount 算法的影响范围在不同的传播概率下具有良好的性能。在Power 网络(图5(c))中,NCSH 与NCA 相比,在各个不同的传播概率情况下均有明显提升,说明NCSH 所选种子节点更为精确。该网络中所有算法的影响范围呈线性增长,DegreeDiscount 算法、pBmH算法和SHDD 表现一般,Degree 算法仍较差。从图5(d)可以看出在CaGrQc 网络中,DegreeDiscount 算法在传播概率较小时影响范围较大,但随着传播概率的增加,其影响范围的增长幅度变小,说明该算法适用于传播概率较小的网络,但当传播概率增大到接近0.1 时,应考虑种子节点对二阶邻居的影响。类似的,SHDD 在后一阶段也使用度折扣算法选择种子节点,因而也受到影响。在CaHepTh 网络(图5(e))中,随着传播概率的增加,NCSH 的影响范围具有最高的增长率,随着种子集的覆盖范围扩大、传播概率的提高,种子节点对邻居的影响范围也越大。从图5(f)可以看出在NetHept 网络中,NCSH 表现最佳,SHDD 表现较差。
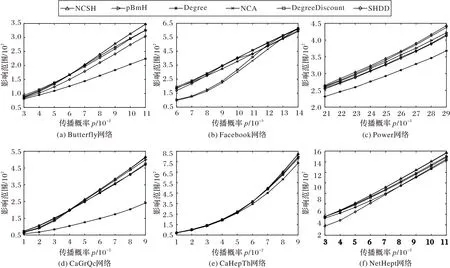
图5 不同算法在六个真实网络中不同p值下的影响范围Fig.5 Influence spread of different algorithms under different p values in six real-world networks
最后,图6 展示了不同算法在CaHepTh 与NetHept 两个较大网络中的运行时间,其余网络上各算法运行时间的大小关系与这两个网络类似。由图6 可知,DegreeDiscount 算法和Degree 算法具有近乎毫秒级的运行时间,NCA 在各个网络中也具有较低的时间开销。pBmH 需要计算所有节点两跳范围内的加权概率和,因此需要的时间高于NCA。NCSH 和SHDD 由于都需要计算网络中所有节点的结构洞指标,因此时间开销比前述几个算法大。而由于NCSH 在不同结构特征的真实网络中均具有最高的影响范围,且随着种子节点规模和传播概率的变化,本算法具有良好的稳定性,因此增加的运行时间在合理范围之内。此外,相较于同样基于结构洞的SHDD,NCSH 在时间上也具有一定优势。
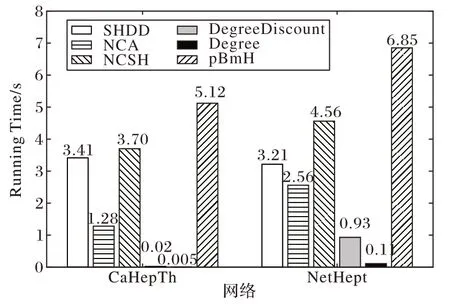
图6 不同算法在两个真实网络中的运行时间Fig.6 Running time of different algorithms on two real networks
5 结语
社交网络影响力最大化是社交网络分析领域的重要问题,本文从多属性融合的角度提出了一种基于覆盖范围和结构洞的影响力最大化算法NCSH。该算法以节点的覆盖范围和结构洞性质作为中心性指标,兼顾节点的覆盖邻居数量和位置优势,有效解决了传统基于拓扑结构的影响力最大化算法性能不稳定的问题。实验结果表明,NCSH 在不同数量的种子集中具有较高的影响范围,在多个真实网络中具有良好的稳定性。

