基于随机分块的稀疏子空间聚类方法

张 琦，郑伯川，张 征，周欢欢

（1.西华师范大学数学与信息学院，四川南充 637009；2.西华师范大学计算机学院，四川南充 637009）

0 引言

聚类分析是数据挖掘领域的关键技术之一，是将一群不相关的对象划分为相似对象的过程。

在许多实际应用中，高维数据通常渐进地存在于低维子空间，其中每个子空间对应一个类。子空间聚类是指将给定的取自于多个子空间并集中的数据点划分到潜在子空间，在运动分割、图像聚类、基因表达聚类等领域都有着重要应用。

无监督数据的存在使得子空间聚类成为高维数据分析的有力工具。常见的子空间聚类方法主要分为四类：基于代数的方法、基于迭代的方法、基于统计的方法、基于谱聚类（Spectral Clustering，SC）的方法。近年来，基于SC 的稀疏子空间聚类（Sparse Subspace Clustering，SSC）算法基于稀疏表示理论，通过对系数矩阵施加

l

约束，获得数据的稀疏表示，从而捕获数据的全局结构。SSC 一经提出，就得到了广泛关注和大量应用。所谓稀疏性就是指用尽量少的原子基来表示数据，即数据的非零系数的个数尽量少。近年来，研究者们在SSC 的基础上进行了不同的拓展：Liu 等提出的低秩表示（Low-Rank Representation，LRR）模型，通过对数据施加低秩约束来获取低秩表示，从而捕获数据的全局结构；低秩SSC（Low-Rank SSC，LRSSC）将SSC 与LRR 相结合，不仅对系数进行稀疏约束，同时在模型中加入低秩约束，结合了稀疏性与低秩性的优点；结构化的SSC（Structured SSC，SSSC）将每个数据点表示为其他数据点的结构化稀疏线性组合，设计了一个统一的优化框架，可以同时学习亲和矩阵和子空间的分割；为了解决SSC 时间复杂度与问题大小的立方成正比问题以及SSC 不处理未用于构造相似度图的样本外数据，可扩展的SSC 采用“采样―聚类-编码-分类”策略来解决可扩展性和样本外问题；内核SSC（Kernel SSC，KSSC）利用核技巧，将SSC 扩展到非线性流形，在高维特征空间中利用非线性解析表示实现了更好的聚类；鲁棒子空间聚类（Robust Subspace Clustering，RSC）提出了一种两步

l

最小化算法，利用泛函分析的思想，解决噪声数据的聚类问题；迭代重加权的SSC（Reweighted SSC，RSSC）算法，相对于传统的

l

最小化框架，不仅提高了算法性能，而且更加逼近

l

最小化框架；基于正交匹配追踪的SSC（scalable SSC by Orthogonal Matching Pursuit，SSCOMP）在广义条件下既提高了计算效率，又保证了保持子空间的亲和性；基于自表达和集群效应的算法，利用集群效应进行自表达，并且使用

l

范数诱导稀疏，解决了SSC 中关联矩阵过于稀疏时忽略同一子空间数据的相似结构问题；基于低秩转换的SSC（SSC with Low-Rank Transformation，SSC-LRT）算法提出了一种结合低秩转换与SSC 相结合的两阶段迭代策略，解决了非独立假设下的聚类问题、随机SSC（Stochastic SSC via Orthogonal Matching Pursuit with Consensus，SCOMP-C）引入Dropout，解决了子空间聚类中的过度分割问题，提升了亲和图的连通性。

在SSC 方法中，如果数据集中数据点个数少，稀疏系数矩阵相对更容易求解，因此本文提出随机分块的SSC 方法，将原问题数据分成几个数据量更少的问题求解。该方法的创新主要包括：

1）将原问题随机划分为

T

个子问题进行求解，将

T

个子问题的稀疏系数矩阵进行组合，然后采用SC 算法实现原问题的聚类；

2）提出了一种随机分块策略与扩充策略，利用该策略实现多个子问题分解和多个子问题系数矩阵的组合。

1 稀疏子空间聚类

稀疏子空间聚类主要包括两个阶段：1）使用稀疏或低秩最小化约束从数据中学习相似度矩阵；2）利用SC 对相似度矩阵进行分割。SC 是否成功很大程度上取决于构建一个信息丰富的相似度矩阵。

稀疏子空间聚类是一种基于自表示的方法。基本思想是：来自

d

维子空间

S

中的任意数据点

y

都可以被表示成来自子空间

S

的其他数据点的一个线性组合。其中，因此，理想情况下，一个数据点的稀疏表示中非零系数的个数对应于潜在子空间的维数。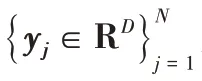

为了找到最稀疏的

c

的解，最小化目标函数为：

然而，

l

范数是非凸优化问题和NP 难的，可用

l

范数来凸松弛

l

范数，原问题可转化为

l

最小化问题：

矩阵形式的公式为：

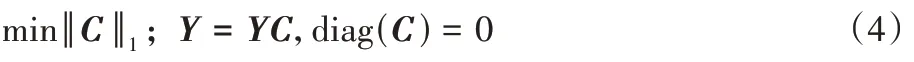
考虑到噪声和离群值：

其中：‖·‖表示Frobenius范数；

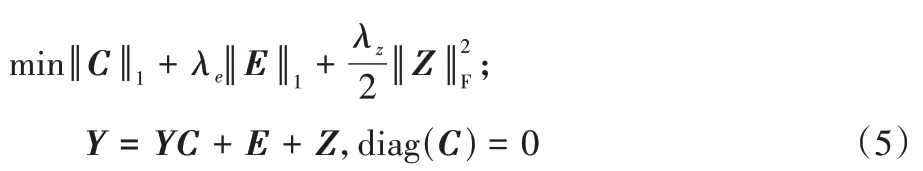
E

∈R表示离群点，

Z

∈R表示噪声；

λ

、

λ

是平衡参数，用于平衡目标函数的三个项。

在一些实际问题中，数据位于仿射子空间而非线性子空间的并集。因此，为了将位于仿射子空间并集中的数据点进行聚类，稀疏优化方程进一步改进为：

利用式（6）中的等式约束，消除

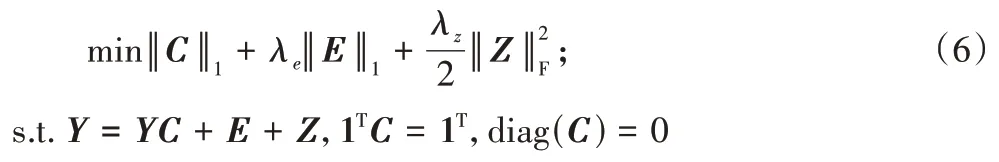
Z

：

引入辅助变量

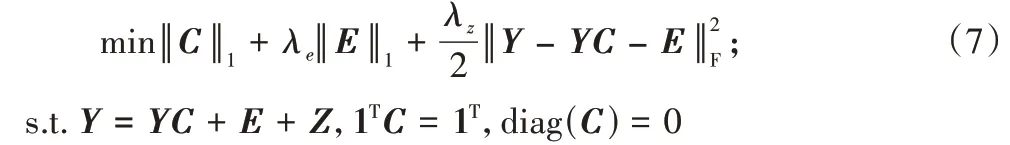
A

∈R，加入参数

λ

，以及2个惩罚项，得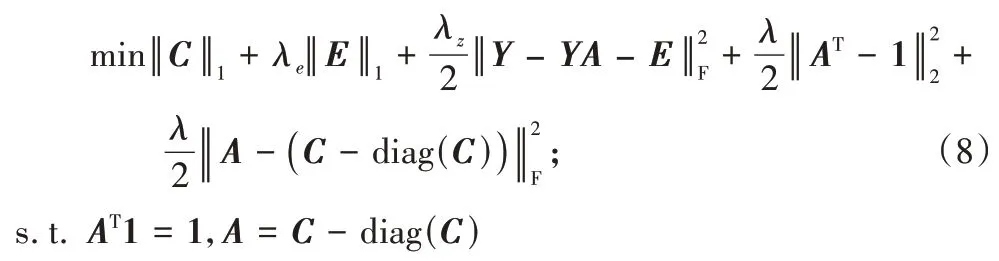

引入拉格朗日乘子

δ

∈R，

Δ

∈R，得到式（6）的拉格朗日函数：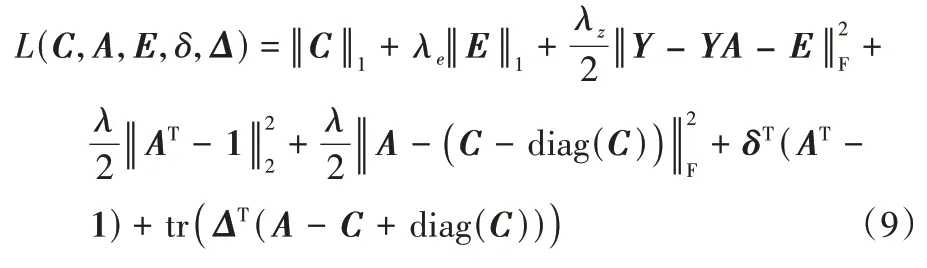

通过交替方向乘子法（Alternating Direction Method of Multipliers，ADMM）求解式（9），可以获得系数矩阵，则相似度矩阵定义为：

将相似度矩阵

W

输入到SC 算法，即可获得最终聚类结果。SSC 的框架如图1 所示。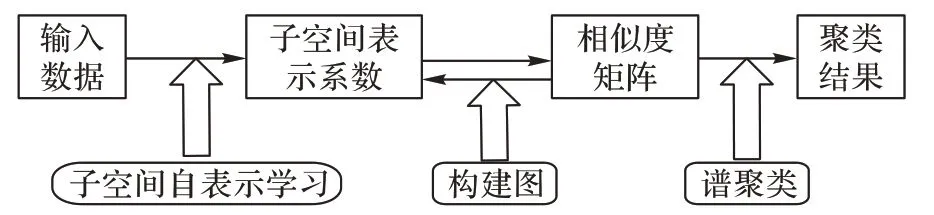

图1 SSC框架Fig.1 Framework of SSC

SC 借助图论的知识，将所有数据点看作空间中的点，点与点之间用边相连，两点之间的距离越远，边的权重越小，反之越大。通过对所有数据点组成的图进行分割，使得不同子图之间边的权重尽可能低，子图内边的权重尽可能高，从而达到聚类的目的。将式（10）作为相似图中点之间的权值矩阵，那么可以利用SC 来对稀疏子空间进行聚类。

算法1 SC 算法。

输入 相似度矩阵

W

。输出 数据集

Y

的

k

子集划分

y

，

y

，…，

y

。步骤1 计算相似矩阵

W

的拉普拉斯矩阵

L

：

步骤3 把

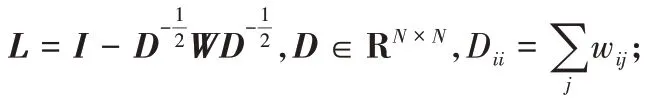
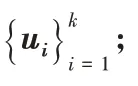
k

个

n

维特征向量列成

n

×

k

的矩阵；步骤4 把生成的矩阵每一行看作

k

维空间的一个向量，使用

K-

Means 聚成

k

类。

2 基于随机分块的稀疏子空间聚类

2.1 算法思想和聚类求解框架

在深度网络的训练过程中，Dropout 技术将神经网络中的每个神经元按照一定的概率使其暂时在神经网络中失效。通过每次随机地使某些神经元失效，减少神经元之间的相互作用，使得网络模型不依赖于某些局部神经元，从而减轻过拟合现象。

受神经网络中使用的Dropout 的启发，本文提出在稀疏子空间稀疏系数矩阵求解过程中引入随机分块策略，将数据集随机划分成几个子集，每个子集作为一个子问题分别求解出系数矩阵

C

，然后将所有子问题的系数矩阵通过扩充后累加成一个相似矩阵

W

，进而进行SC。基于随机分块的SSC 的框架如图2 所示。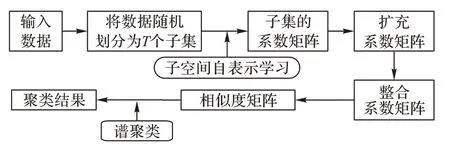

图2 基于随机分块的SSC框架Fig.2 Framework of SSC based on random blocking

2.2 数学模型

基于随机分块的SSC 将原问题转换为

T

个子问题，每个子问题的目标函数可以采取以下形式：

其中：

Y

表示第

t

（

t

=0，1，2，…，

T

）个子问题的数据集的矩阵形式；

C

表示第

t

个子问题的系数矩阵。

在现实世界中，大多数是噪声数据集，所以子问题目标函数采用以下形式：

其中：

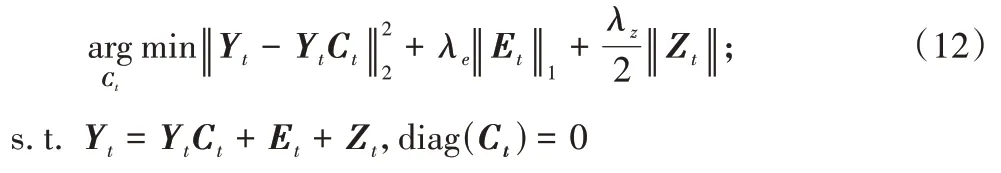
E

表示第

t

个子问题的离群点；

Z

表示第

t

个子问题的噪声。

2.3 随机分块策略

基于随机分块的SSC 将原问题的数据集划分成几个子集分别求解稀疏系数矩阵。对原问题的数据集的划分采用如下的随机分块策略进行：

设

idx

是1 到

N

的

N

个数构成的随机序列，

idx

是指标集，表示每个数据点在数据集

Y

中所处的列指标；设

k

是每次从数据集中选择的数据比例数。随机分块策略是每次从指标集

idx

中选择连续的

k

*

N

个数据构成一个指标集子集，然后根据指标集子集从数据集中获得子问题的子数据集。随机分块策略具体操作如下：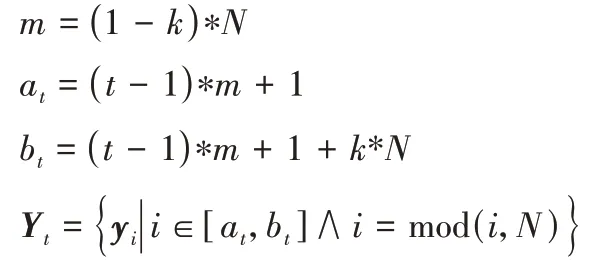

其中：

m

表示每次前进的步长；

Y

表示第

t

个子问题的数据集；

a

表示子集

Y

的指标集的开始位置；

b

表示子集

Y

的指标集的结束位置；函数mod(

i

，

N

)是求余函数。

2.4 子问题系数矩阵的扩充策略

求得每个子问题的系数矩阵后，需要将

T

个子问题的系数矩阵进行整合。首先将每个子问题的(

k

*

N

)*(

k

*

N

)维系数矩阵

C

扩充为

N

*

N

维的系数矩阵

C′

；然后将子问题系数矩阵进行叠加得到

C′′

；最后，将叠加后的系数矩阵的每个单元值除以该单元对应的两个数据点被同时分配相同子集的次数，从而得到最终的系数矩阵

C

。

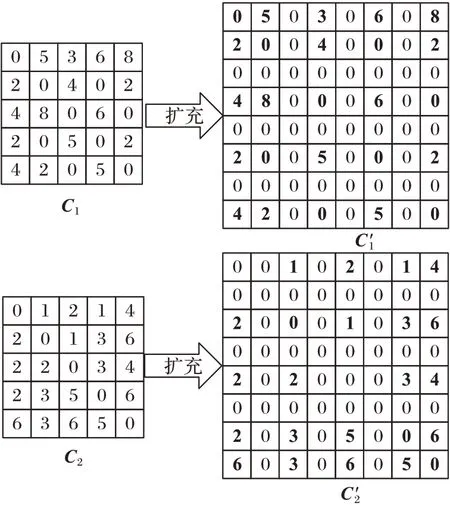
图3 系数矩阵的扩充Fig.3 Expansion of coefficient matrix

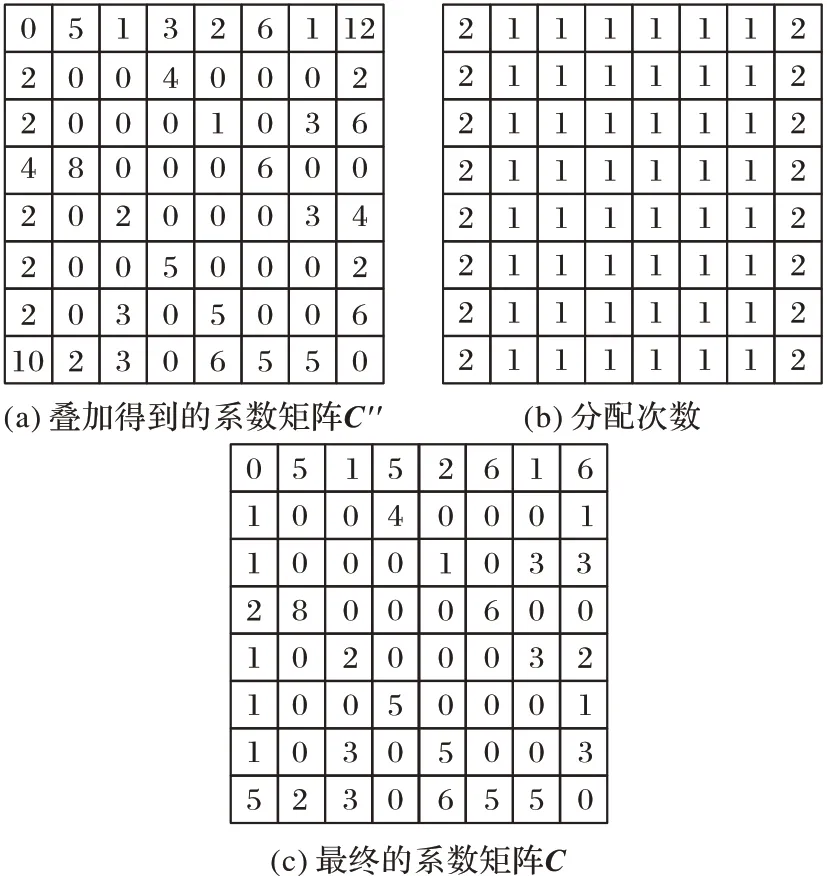
图4 系数矩阵整合Fig.4 Coefficient matrix integration

2.5 交替方向乘子算法求解子问题

使用交替方向乘子法（ADMM）可以求解拉格朗日函数式（9）的最小值，从而求得系数矩阵

C

。

算法2 交替方向乘子算法。

输入 数据集

Y

。输出 系数矩阵

C

。

步骤1 设置参数：

步骤2 初始化变量

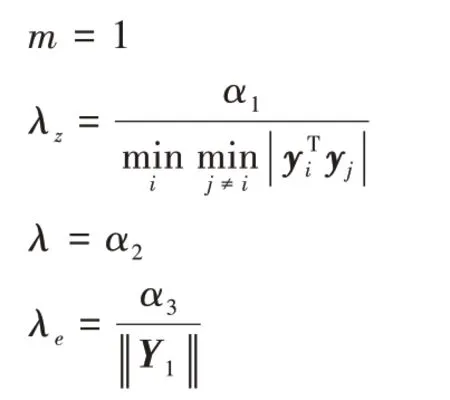
i

=0，

A

=0，

C

=0，

δ

=0，

E

=0，

Δ

=0

步骤3 重复以下步骤直到算法收敛或迭代达到最大次数：

步骤3.1 固定(

C

)，

E

)，

δ

)，

Δ

))，通过更新

A

极小化

L

：

其中：

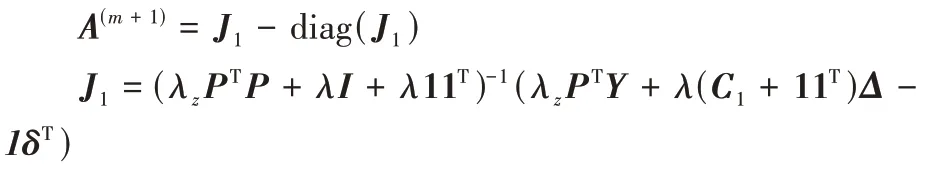
P

=[

Y

，

I

/

λ

]，

C

=[

C

；

λE

]步骤3.2 固定(

A

)，

E

)，

δ

)，

Δ

))，通过极小化

L

更新

C

：

其中：Γ=min(|

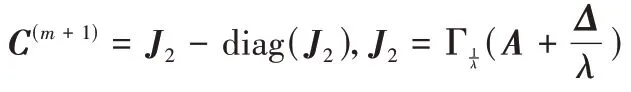
v

|-

η

，0)*sign(

v

)步骤3.3 固定(

A

)，

C

)，

δ

)，

Δ

))，通过极小化

L

更新

E

：

步骤3.4 固定(

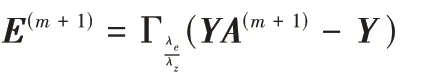
C

)，

E

)，

A

))，更新(

δ

，

Δ

)：

步骤3.5

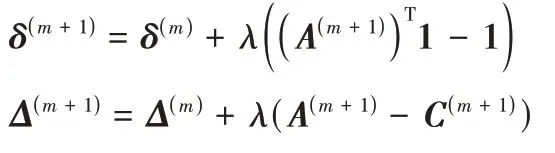
m

=

m

+1

2.6 完整算法

式（12）的求解分两阶段迭代进行：第一阶段，对数据集进行2.2 节中的随机分块操作，将原问题转化为

T

个子问题；第二阶段，根据SSC 算法求出当前子问题的系数矩阵，然后将

T

个系数矩阵进行根据2.4 节的扩充策略进行整合，最后对整合后的系数矩阵进行聚类。具体算法如下：

算法3 基于随机分块的SSC。

输入

D

×

N

的矩阵

Y

，参数

m

，

α

，

α

，

α

，

k

，

T

。

输出 聚类结果。

步骤1 将原数据按照2.3 节的随机分块策略随机划分成

T

个子集

Y

，

Y

，…，

Y

，从而将原问题划分为

T

个子问题；步骤2.1 针对每个子问题的数据矩阵

Y

，执行算法2，获得每个子问题的系数矩阵

C

；步骤2.2 将每个子问题的系数矩阵

C

按照2.4 节的扩充策略，扩充成

N

×

N

维的系数矩阵

C

′；步骤3 将

T

个系数矩阵

C

′进行叠加，叠加之后，每个单元值除以该单元对应的两个数据点被同时分配相同子集的次数，从而得到原问题的系数矩阵

C

；步骤4 采用式（10）构建相似矩阵

W

；

步骤5 采用算法1，进行SC。

3 实验与结果分析

实验中，针对不同的聚类目标数量，首先，对不同的选点比例和子空间数进行实验，探究选点比例与子空间数对聚类误差的影响；然后选择最优的选点比例与子空间数，将本文提出的方法与稀疏子空间聚类（SSC）、随机稀疏子空间聚类（SCOMP-C）、基于正交匹配追踪的稀疏子空间聚类（SSCOMP）、谱聚类（SC）和

K

均值（

K

-Means）进行比较。

3.1 数据集

本文使用Extended Yale B 人脸数据集进行实验。Extended Yale B 数据中每张图像的像素均为192*168，总共有38 个人，每个人有64 张在不同光照条件下的正面人脸图像。将所有人脸图像的大小调整为16×14，并将每张图像转换成一个224 维向量。因此，被聚类的每个数据点有224 维，属于高维聚类问题。图5 展示了人脸数据集中10 个人在不同光照条件下的部分图片。

图5 人脸数据集的部分图片Fig.5 Part images in face dataset

3.2 评价指标

为了评估聚类算法的性能，采用了4 个度量指标：子空间聚类误差（Subspace clustering error）、互信息（Mutual information）、兰德指数（Rand index）和熵（Entropy），它们的定义分别为式（13）～（16）：

其中：

X

是数据点的一种划分；

Y

是数据点的另一个划分；

n

为数据点的数量；

TP

为划分正确的数据点数量；

TN

为划分错误的数据点数量。

子空间聚类误差用于衡量聚类准确率，聚类误差越小越好；互信息、兰德指数均用于衡量数据分布的吻合程度，取值范围为[0，1]，其值越大越好；熵用于衡量变量的不确定程度，值越小越好。

3.3 实验结果与分析

算法3 中的三个参数

α

、

α

、

α

均设置为20，

m

=150，

k

表示选点比例，

T

表示子问题数。为了探索算法针对不同目标数的性能，实验分别对不同的聚类目标数：

Subjects

∈{2，3，4，5，6，7}进行实验，此时，数据矩阵

Y

的大小分别为224 ×(64 ×

Subjects

)。表1 展示了当子问题中数据点的数量按照比例选择时，选点的比例与子问题的数量对实验结果中的聚类误差的影响。其中，

T

∈{5，6，7，8，9} 表示子问题的个数，

k

∈{0.7，0.75，0.8，0.85，0.9}表示选点的比例，黑体字表示最优项。在

Subjects

∈{2，3，4，5，6，7}的实验中，无论

k

，

T

取何值时，效果均优于SSC。当

k

=0.85 时的聚类误差几乎都小于其他选点比例的聚类误差，且随着

T

的增加，聚类误差逐渐降低，而后趋于平稳。故本文按照

k

=0.85 的比例选择每个子问题的点数，子问题数为

T

=8。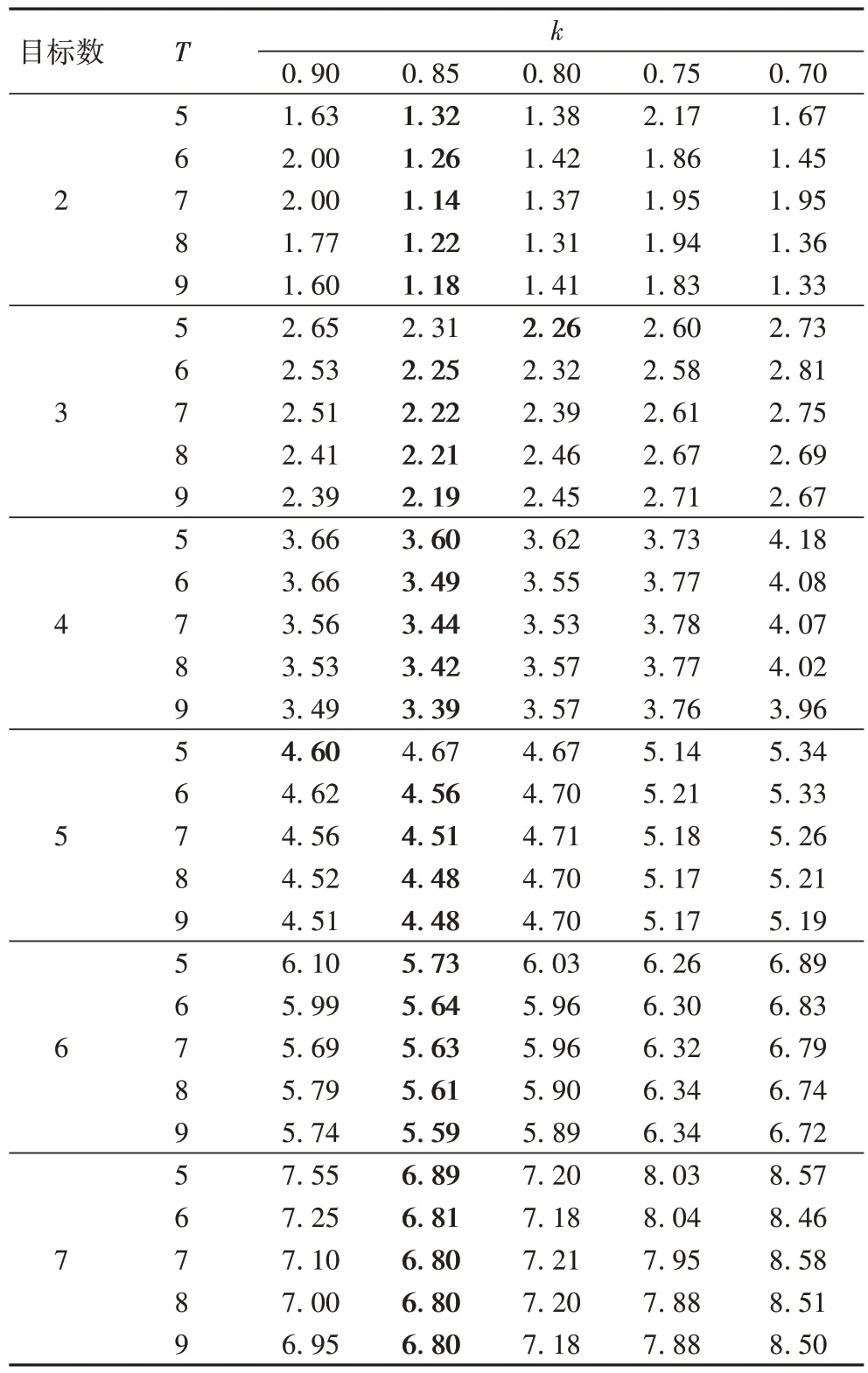

表1 子问题数与选择数据点的比例对聚类误差的影响Tab 1 Influence of ratio of number of sub-questions to selected data points on clustering error

表2 展示了当

k

=0.85，

T

=8 时，本文方法在人脸数据集上与SSC、SCOMP-C、SSCOMP、SC 和

K

-Means 算法进行比较的实验的结果，其中黑体字表示最优项。可以发现：在

Subjects

∈{2，3，4，5，6，7}时，本文方法的聚类误差和熵均比其他对比方法小，而互信息和兰德指数相较于其他对比方法大。其中，相较于5 种对比方法中的最优方法，聚类误差平均降低了3.12 个百分点，熵平均降低了6 个百分点，互信息提升4 个百分点，兰德指数提升2 个百分点。说明与其他算法相比，结合了随机分块策略与扩充的SSC 算法显著优于其他5 种方法。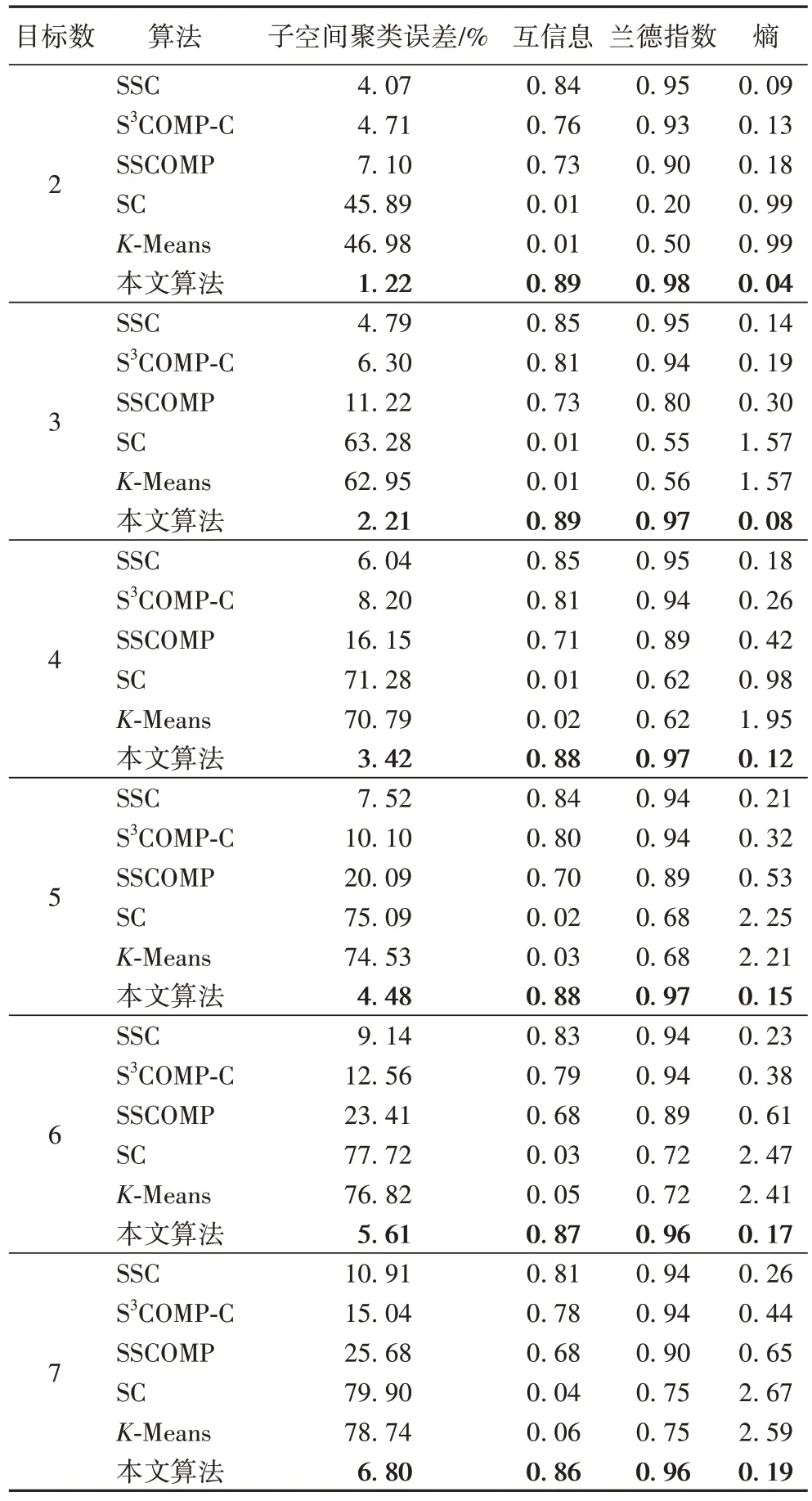

表2 Extended Yale B数据集中不同数量对象的人脸图像的5种聚类评估（k=0.85，T=8）Tab 2 Five clustering evaluations of face images with different numbers of objects in Extended Yale B dataset（k=0.85，T=8）

4 结语

本文提出了一种基于随机分块的SSC 方法，每次随机选择固定数量的点，将原问题转换为

T

个子问题进行求解，将原优化问题重新表述为一组小规模子问题上的聚类问题。还探索了选点比例以及子问题数对实验结果的影响。在人脸数据集上的实验结果表明，本文方法显著优于其他5 种方法。