基于动态加权函数的集成分类算法

王 乐，韩 萌，李小娟，张 妮，程浩东

（北方民族大学计算机科学与工程学院，银川 750021）

0 引言

在动态变化和非平稳环境中数据以流的形式到达，要从大量的数据中获取有用的知识，数据流挖掘方法在大数据领域起着重要的作用。为了适应不断变化的数据流，将数据流更有效地转变为有用的信息供人们在生活中使用，集成分类无疑是一种优秀的挖掘数据流的方法。集成分类算法之所以受到众多研究者的青睐，是因为集成分类器由多个准确而多样的基分类器组成，可以形成分类决策，采用不同的加权方式可以构建多种多样的决策，从而使其性能优于单个分类器。在集成方法中，Bagging和Boosting被认为是最流行和最有效的方法。Bagging 是一种引导聚集算法，生成不同的模型并使用这些模型获得集成分类器的方法。它通过降低基分类器的方差改善了泛化误差，使用不同的模型对实例进行预测，在预测类别时进行多数票投票对模型进行平均操作，最后提高整个分类器的准确性。Boosting 通过对样本集进行操作得到样本子集，将弱分类算法作为基分类器放入Boosting 框架中然后对训练样本集进行训练生成基分类器，重复运行给定的弱学习算法，这样经过

n

轮迭代就会产生

n

个基分类器，把这样的分类器集成在一起就可以提高弱分类算法的识别率。除去Bagging 和Boosting 这两个经常被提及使用的算法，Stacking 同样受到众多研究学者的青睐，Stacking 是集成学习的第三类，广泛应用于有监督学习和无监督学习领域，基分类器的输入属性和学习策略对Stacking 的性能有很大的影响。例如，Todorovski 等提出了一种称为元决策树（Meta Decision Tree，MDT）的Stacking 方法来改进集成学习过程。Zhu 等还提出了一种称为Stacking 数据包络分析（Data Envelopment Analysis，DEA）的方法来找出最佳Stacking 方式。David 等提出了一种新颖的通用面向对象投票和加权自适应Stacking 框架，用于利用分类器集成进行预测。这个通用框架基于任何一组基础学习器的概率的加权平均值运行，最终预测是它们各自投票的总和。

虽然集成分类算法已经可以处理一些数据流的分类问题，但是在基分类器的加权以及动态更新以及基分类器的选择上仍然存在一些问题，在分类的过程中产生的这些问题仍然会影响分类的准确率和时空效率。所以针对现有的集成分类算法，本文设计了一种基于动态加权函数的集成分类算法，主要工作如下：

1）本文提出了一个加权函数

F

（

x

，

y

，

d

，

θ

）调节基分类器权重，将其应用于基分类器的评价以选择更适合的分类器，其中：

x

表示实例，

y

表示实例的类别，

d

表示数据块中的样本个数，

θ

表示两个权重的折中系数；该加权函数采用精度权重和性能权重按一定比例计算的综合权重来对基分类器进行加权，通过这个加权函数的评价结果选出最优的分类器增加集成的性能。2）为更好地提升集成分类器的性能，本文还设置了候选分类器对基分类器进行替换，并提出了一个权重函数

G

（

x

，

y

，

θ

），其中：

x

表示最新数据块上的实例，

y

表示

x

的类别，

θ

表示两个权重的折中系数；通过这个函数可以得到候选分类的权重，候选分类器替换集成中最差的分类器，就可以得到更好的分类结果。

3）本文提出了一种基于动态加权函数的集成分类算法（Ensemble classification algorithm based on Dynamic Weighting function，EDW），使用不断更新的数据块训练分类器，使用候选分类器来替换集成中最差的分类器，采用了两个加权函数动态更新基分类器，其中基分类器选用泰勒定理和正态分布性质的不等式的决策树。

1 相关工作

在集成分类算法的相关研究中，除了基于Bagging、Boosting 和Stacking 的算法，基于块的算法在集成分类中仍然是一个研究热点。基于块的集成输入固定大小的样本块重新评估集成分类器，并用根据最新样本训练的分类器替换最差的基分类器。动态加权多数不平衡学习（Dynamic Weighted Majority for Imbalance Learning，DWMIL）逐块处理不平衡的数据流使其更加稳定。DWMIL 为每个块创建一个基分类器，并根据在当前块上测试的性能来衡量它们。因此，最近训练的分类器或类似于当前块的概念将在集成中获得高权重。因此，如果当前的概念与创建分类器时的概念相似，则分类器可以持续更长的时间来对预测作出贡献。基于自适应块的动态加权多数（Adaptive Chunk-based Dynamic Weighted Majority，ACDWM）是一种基于块的增量学习方法，可以处理包含概念漂移的不平衡流数据。ACDWM 利用集成框架，根据当前数据块的分类性能动态加权各个分类器。通过统计假设检验自适应地选择数据块大小，以判断基于当前数据块构建的分类器是否足够稳定。因为ACDWM是完全增量的所以不需要存储之前的数据，并且在概念漂移环境下可以自适应地选择块的大小，相较于最先进的基于块的方法和在线方法ACDWM 效果都很出色。Ren 等提出了一种基于块的数据流分类器称为知识最大化集成（Knowledge-Maximized Ensemble，KME），KME 算法结合了在线集成和基于块的集成的元素，可以用有限的标记观测来解决各种各样的漂移场景，保存过去块中的标签，被重复使用以提高候选分类器的识别能力，可以最大限度地利用数据流中的相关信息，这对于训练数据有限的模型是至关重要的。KME 算法还可以使用监督知识和非监督知识识别周期性概念，评估集成成员的权重。精度更新集成（Accuracy Updated Ensemble，AUE2）结合了精确的基于块的加权机制和Hoeffding 树的增量特性，在训练样本中固定大小的块中顺序地生成基分类器，当一个新块到达集成时，现有的基分类器被评估并更新它们的组合权重。在集成中加入从最近块中学习到的分类器，并根据评价结果删除最弱的分类器。

动态加权多数（Dynamic Weighted Majority，DWM）算法是一种增量集成算法，在每个样本输入后，根据递增的分类器的准确率对其进行加权。每当DWM 的一个基分类器分类错误，它的权重就会按用户指定的因子降低。动态更新集成（Dynamic Updated Ensemble，DUE）算法循序渐进地学习新的概念，不需要访问以前的知识，同时采用分段加权法加权，先前集成成员的权重基于其在最新实例和稳定性水平上的表现，通过使用动态调整基准组权重的方法还可以解决概念漂移问题。Zhao 等提出了一种加权混合Boosting集成方法（Weighted Hybrid Ensemble Method on Boosting，WHMBoost）对二值分类数据集进行分类并结合了两种数据采样方法和两种基本分类器，每个采样方法和每个基分类器都分配有相应的权重，以便它们在模型训练中有不同的贡献。该算法综合了多采样方法和多基分类器的优点，提高了系统的整体性能。Ancy 等提出了一种基于权值机制的集成成员更新的方法来处理概念漂移，集成分类器利用增量分类器作为加权组件，根据数据类别为候选模型分配权重，较高的权重表示分类器可以获得更好的准确性，如果分类器表现不佳，则分配一个较低的权重。当达到集成大小时，候选分类器将替换最差的分类器，否则直接将候选分类器附加为集合的成员。Sidhu 等提出了一种多样化动态加权多数（Diversified Dynamic Weighted Majority，DDWM）的在线集成方法，来分类具有不同概念分布的新数据实例，以便准确地处理各种类型的概念漂移。如果集成中的分类器错误的分类了给定的实例，那么就将该分类器的权重减少一个固定的乘数，如果在后续训练中该分类器仍然表现不佳，当其权重达到一个固定的阈值，就将该分类器从集成中删除，还使用了一个固定的参数来控制权重的更新以及分类器的创建和修剪，使其在具有概念漂移的数据集中取得更好的分类效果。

2 本文算法

为了使算法更易描述，现对算法要用到的一些问题进行符号化，其中

B

表示第

i

个数据块，数据块中包含

n

个实例，分别为(

x

，

y

)，(

x

，

y

)，…，(

x

，

y

)，

x

是特征向量，

y

是类标签，

ε

表示分类器的集合，其中分类器有

k

个。随着数据块的不断更新，数据流也在不断变化，旧的数据已经不能代表最新的概念，训练出的分类器也不能得到一个很好的结果，所以算法就要对基分类器进行更新与代替，本文采用的集成成员的更新方法是使用精度权重以及性能权重的综合权重来对其分类器进行调整，以替换掉效果不好的分类器使整个集成算法达到最优的效果。

2.1 权重更新方法与基分类器

2.1.1 集成成员精度权重更新新方法

精度更新集成算法维护一个加权的基分类器池，并通过使用加权投票规则，结合基分类器的预测结果来预测传入样本的类别。在处理完每个数据块之后，创建一个分类器，替换性能最差的集成成员。根据在最新数据块中对样本数据估计其预期的预测误差，可以评估每个基分类器的性能。在替换了表现最差的分类器后，对其余的集成成员进行更新，即增量训练，并根据它们的精度调整其权重。

传统的精度集成更新算法使用均方误差（Mean Square Error，MSE）用来计算分类器的均方误差进而计算权重，例如精度更新集成AUE2，MSE 显示了实际类标签

y

的估计概率的误差，一个给出精确概率估计的模型可以降低该误差。虽然它使用真后验概率

P

(

y

|

x

)作为初始定义的答案，但在真实数据集中通常不知道

P

（

x|y

）。一般情况下，MSE是根据经验计算的假设

P

(

y

|

x

)=1。在文献［15］中，提出了MSE 分类器评价指标计算公式：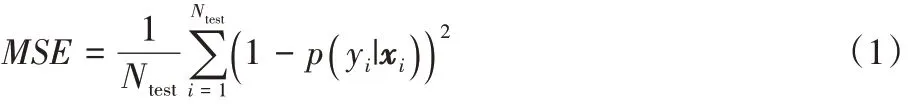

MSE

通常被用作估计概率的度量，其中分子为误差平方和，分母的值为自由度；但是如果概率估计不稳定，即使模型能够正确地预测出所有的类标签，

MSE

仍然会变得很高，计算出的值无法更好地选择分类器，所以，Fan 等引入了改进后的平方误差（Integrated Square Error，ISE）。ISE 仅在模型对样本分类错误时才会解释概率误差。也就是说，ISE 将准确率和

MSE

结合成一个值，并且假设二进制分类中估计概率的预测阈值固定为0.5。ISE 分类器评价指标计算公式为：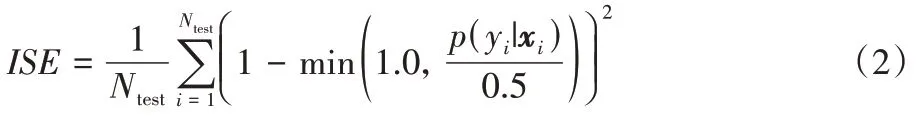

使用改进后的平方误差ISE 作为新的度量方法，就可以避免使用MSE 时出现概率估计不稳定产生错误的情况。将改进后的均方误差公式代入基于块的数据流的思想中就可以得到式（3）：

其中：函数

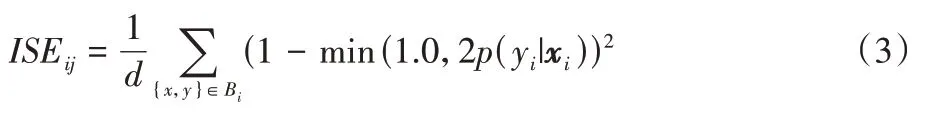
P

(

y

|

x

)表示分类器

C

给出的

x

是属于类

y

的实例的概率，数据块

B

上有

d

个样本，不考虑单个类的预测，而是考虑所有类的概率；

ISE

的值表示在块

B

上的分类器

C

的预测误差，数据块

B

上有

d

个样本。AUE2 算法中提出的随机预测的分类器的均方误差

MSE

公式为：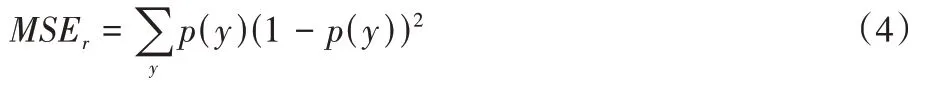

其中：

p

(

y

)是类别

y

的分布，可以通过式（3）～（4）计算数据块上的分类器的预测误差和随机预测分类器的均方误差，从而提出并计算基分类器的权重公式

f

(

x

，

y

，

d

)：

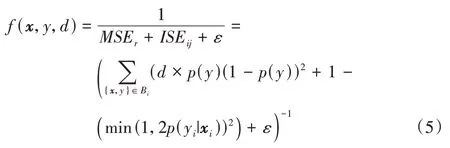
ISE

的值表示在块

B

上的分类器

C

的预测误差，而

MSE

是随机预测的分类器的均方误差，并用作当前类别分布的参考点。另外一个非常小的正值

ε

是为了避免被零除的问题。式（5）中给出的权重公式旨在结合分类器的准确率信息和当前的类分布情况，因为本文使用的权重公式是非线性函数，与类似于精度加权集成（Accuracy Weighted Ensemble，AWE）算法中使用的线性函数相比，本文提出的EDW 可以高度区分基分类器。除了给集成成员分配新的权重，每个数据块

B

都用一个被记为

C

′的候选分类器，这个分类器是从最近块中的样本中创建的。

C

′在最近的数据上训练，并且把它当作为一个“完美”分类器，同时根据如下公式分配一个精度权重。EDW 不但为集成中的成员分配权重，同时还维护一个候选分类器池，为每个数据块

B

都分配一个候选分类器

C

′，并且把这个候选分类器

C

′默认为一个没有误差的分类器，其中，候选分类器的权重计算公式如式（6）所示：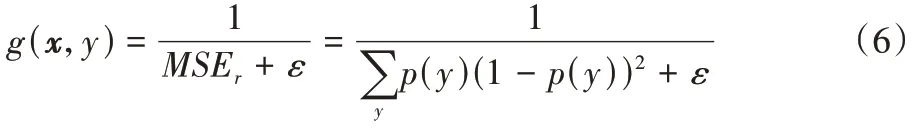

与用于给当前的集成成员分配权重的函数相比，候选分类器的权重没有考虑

C

′在

B

数据块上的预测误差，这种方法是基于最近的数据块能够最好地表示当前和未来的数据分布的假设决定的。因为

C

′是在最近的数据上训练的，它应该被视为可能是最佳的分类器。

2.1.2 集成成员性能权重更新方法

在对基分类器的精度权重进行了计算之后，下面将对基分类器的性能权重进行计算，因为在先前数据块上训练的基分类器的权重是基于最新数据块中样本的分类性能的，由此本文提出了式（7）对最新数据中的基分类器进行性能权重的更新，性能权重用

h

（

x，y

）表示：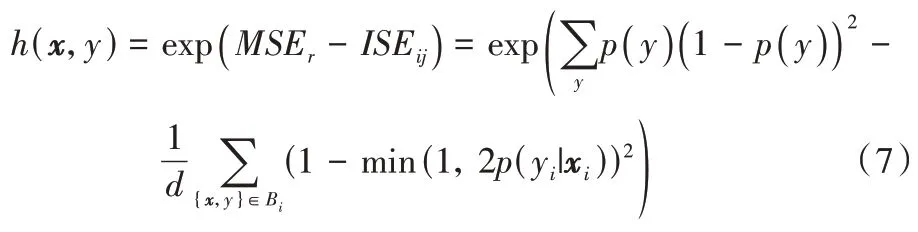

式（7）中给出的绩效权重结合了分类绩效和当前类别分布的因素，之前的基分类器的性能权重应与

ISE

成反比。因此，保留的先前基分类器的性能权重需要评估当前数据块的均方误差。通常认为最新块的数据分布是当前和未来一段时间概念的最佳代表，因此，可以不管其分类性能如何将候选分类器

C

′的性能权重直接设定为最优值。用

f

′(

y

)表示的候选分类器

C

′的性能权重可以表示为：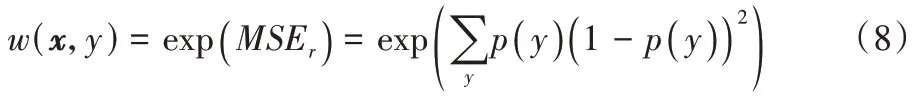

候选分类器

C

′的性能权重与随机预测的均方误差成正比。因此，候选集成成员的判别能力仅考虑当前的类分布。因为在式（8）提出的性能权重不需要计算模型的均方误差，所以不需要额外的验证集来验证

C

′的分类性能。因此该算法的加权机制不需要交叉验证过程，该过程适合处理快速数据流。同时，如果将候选分类器视为最佳成员，则该算法可以很好地应对突然的概念漂移。

最后提出式（9）～（10），通过公式可以得到的集成的综合权重，其定义为精度权重和稳定性权重的组合，如下所示：

其中：

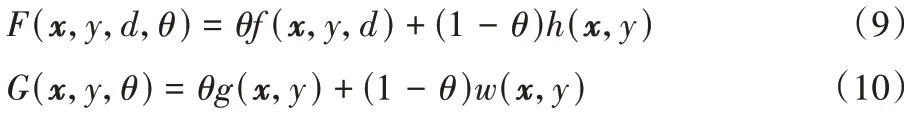
F

(

x

，

y

，

d

，

θ

)计算分类器的权重，

G

(

x

，

y

，

θ

)计算候选分类器

C

′的权重；

f

(

x

，

y

，

d

)和

h

(

x

，

y

)分别是基分类器精度权重和性能权重函数；

g

(

x

，

y

)和

w

(

x

，

y

)分别是候选分类器的精度权重和性能权重函数；

θ

是性能权重和基分类器的稳定性之间的折中系数，通常取

θ

=0.5。

2.1.3 基分类器的选择

本文提出的集成算法使用基于泰勒定理和正态分布的性质推导出的不等式来作为分裂节点判断标准的决策树作为基分类器，这种决策树不仅适用于数值型数据也适用于具有名称型属性值的数据，而且还易于解决概念漂移问题，该不等式可以根据有限的数据样本进行分割并且辨别当前节点的最佳属性其是否也是整个数据流的最佳属性。分裂节点的判断标准公式为：

其中：

Z

(1 -

α

)是标准正态分布（0，1）的第1 -

α

个分位数；改进后的决策树中用到的不等式（式（11））对数据集的适应性更高，所以可以使用式（12）来控制分裂标准：

其中：

k

为类的数目；那么

G

(

x

)大于

G

(

x

)的概率为1 -

α

。

下面对节点进行信息增益的计算，信息增益根据信息增益最大的属性作为分裂点，其公式为：

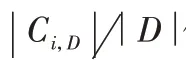
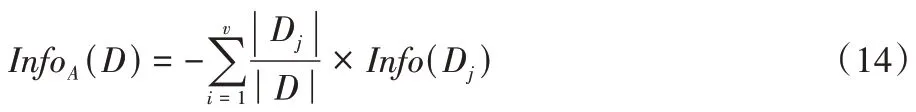
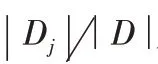
信息增益定义为原来的信息需求与新的信息需求之间的差。即

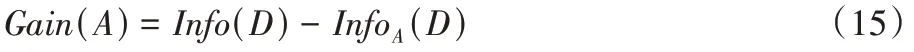
定理1

考虑两个属性

x

和

x

，经过计算得到信息增益函数的值，如果这些值的差满足以下条件：

当两个信息增益差值大于通过式（11）计算得到的

μ

时，就对该节点进行分裂，生成新的叶子节点。这种节点分裂判定方法可以根据有限的数据样本得到分割节点并判断该最佳属性是否也是整个数据流的最佳属性。结合基于泰勒定理和正态分布的不等式和更精确的分裂准则研究与设计一种新的数据流决策树分类算法以获得更佳的分类性能，该公式允许确定数据流元素的最小数量，这样树节点就可以根据所考虑的属性进行划分。

EDW 伪代码如下所示。

算法1 EDW。

输入 被划分为块的数据流

S

集成成员个数

k

；内存限制

m

；

k

个权重增量分类器的集合

ε

。输出：

k

个分类器。

算法2 基分类器的训练。

输入 数据流实例

S

，属性集

X

，分裂评价函数

G

（

X

），分类置信度

δ

，主动分裂阈值

τ

，最小分裂实例数

n

。

输出 决策树DT。

综上所述，本文提出的基于动态加权函数的集成分类算法，首先向集成分类器中传入被分为块的数据流，如果当前分类器集合为空，则在这个块上使用训练后的分类器构建候选分类器，使用

B

上的分类器

C

的值计算

ISE

，使用改进后的平方误差ISE 作为新的度量方法，避免使用MSE 时出现概率估计不稳定产生错误的情况，计算分类器的权重以及候选分类器的权重。当当前分类器集合

ε

中分类器的数量小于

k

，就将候选分类器加入当前分类器集合中，否则就用候选分类器代替原分类器集合

ε

中的最差的分类器；使用下一个数据块

B

再次训练分类器，当集合

ε

中的分类器数量达到

k

时，则比较分类器权重使用候选分类器替换

ε

中权重最低的分类器。在最后如果内存的使用超过了限制，就对分类器进行修剪，最后就可以得到训练好的集合分类器，使用训练好的集成分类器对数据进行分类得到一个可观的分类结果。其中EDW 训练分类器的流程如图1 所示。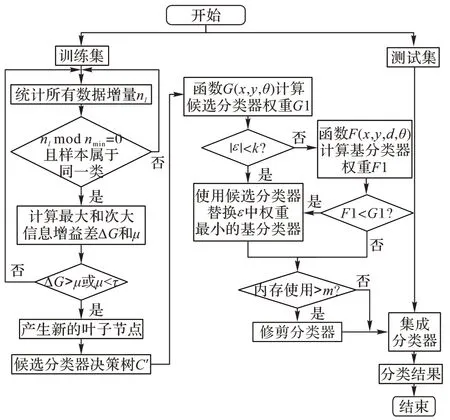

图1 EDW训练分类器流程Fig.1 EDW algorithm training classifier flow

2.2 EDW实例

在2.1 节已经对EDW 的思想和流程进行了详细的介绍，为方便对算法性能的理解，本节将以实例介绍。因为该算法是基于块的集成，所以该算法给定一个数值属性的数据集，在后续演示中将对其进行详细的介绍，样本点表示该点数据信息的坐标值，类标是该数据集的标签。

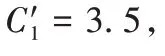
其中3 个数据块中，每个数据块设有6 个样本，具体样本实例如表1 所示。

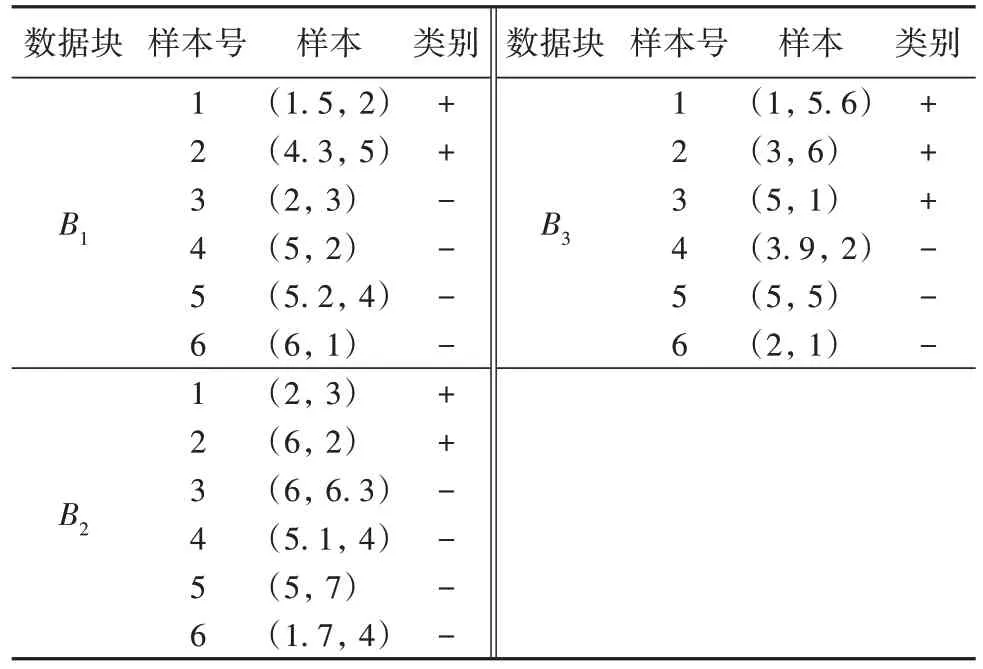
表1 数据块实例样本Tab 1 Data block instance samples

1）第一个数据块到达。

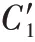
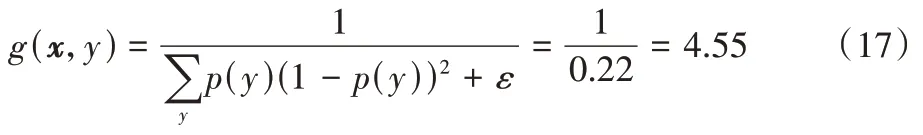
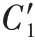
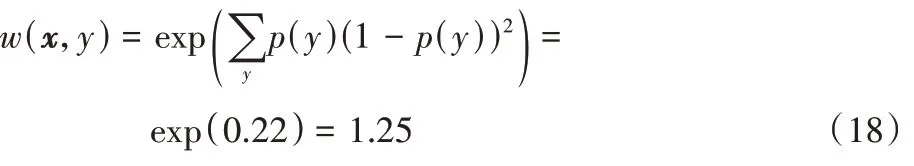
权重最终为：

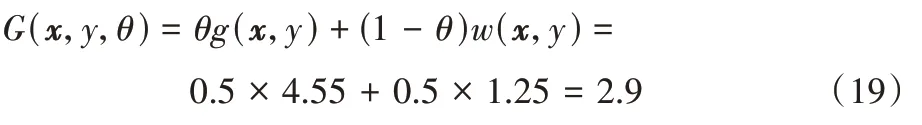
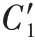
2）第二个数据块到达。

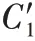
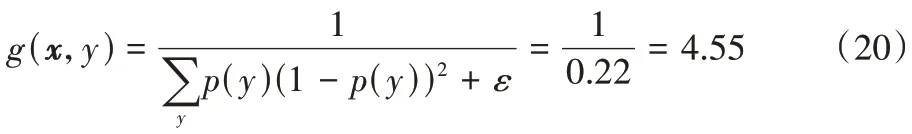
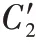
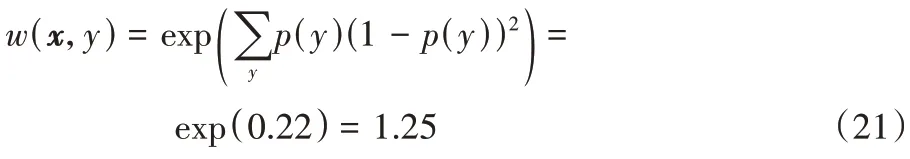
权重最终为：

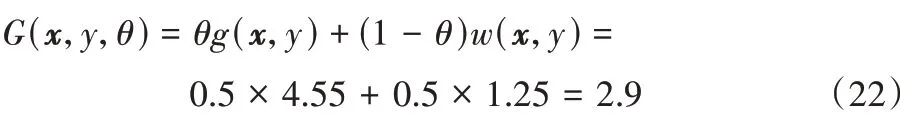
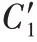
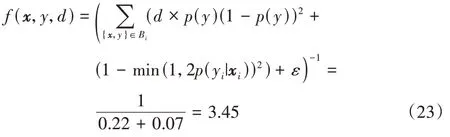
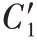
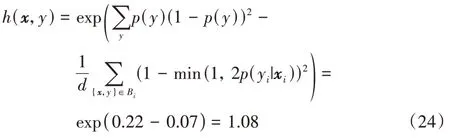
其权重最终为：

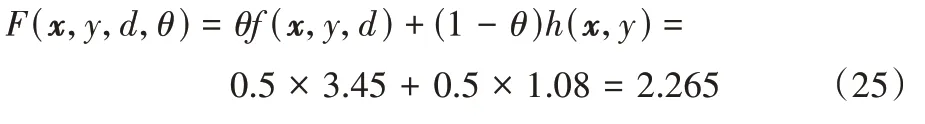
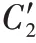
3）第三个数据块到达。

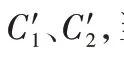
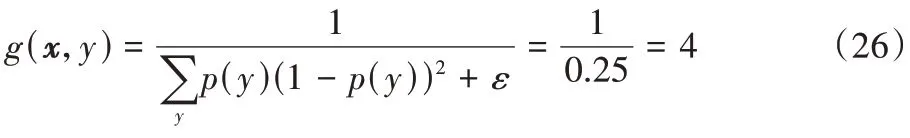
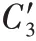
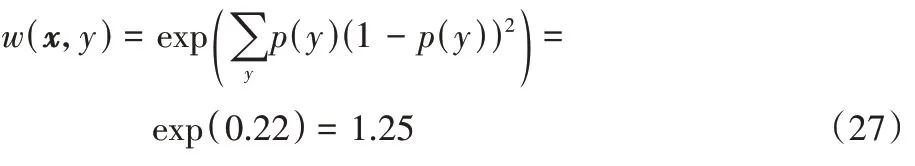
权重最终为：

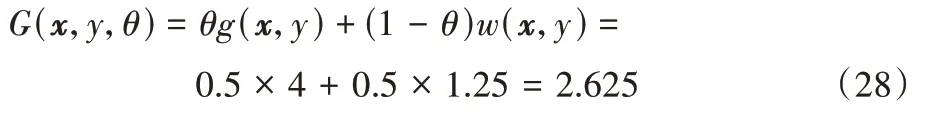
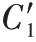
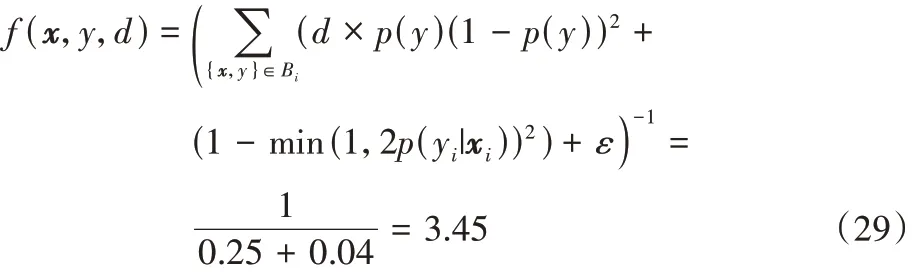
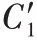
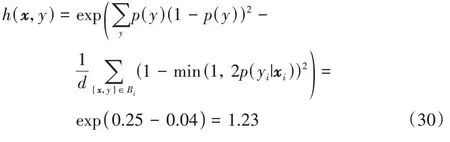
其权重最终为：

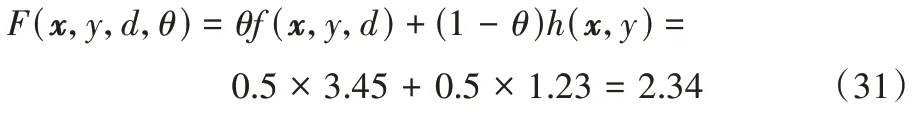
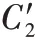
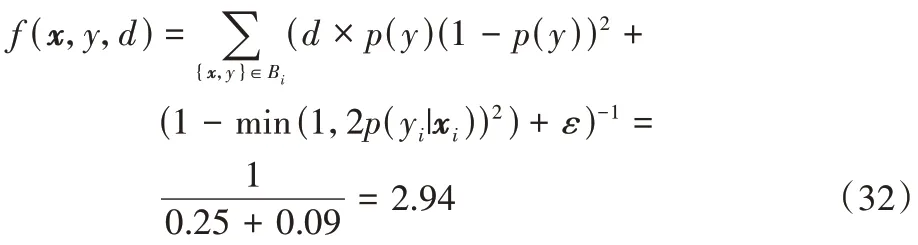
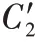
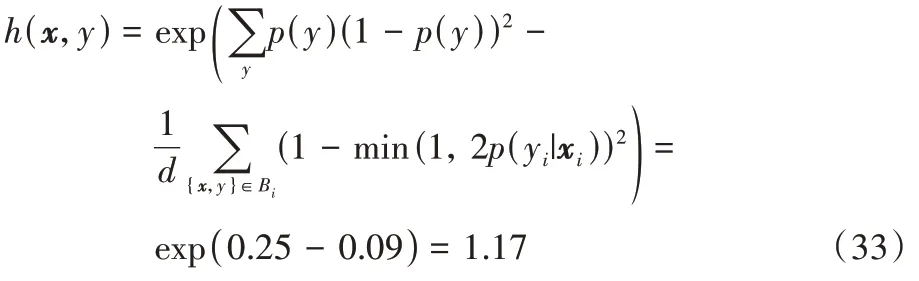
其权重最终为：

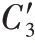
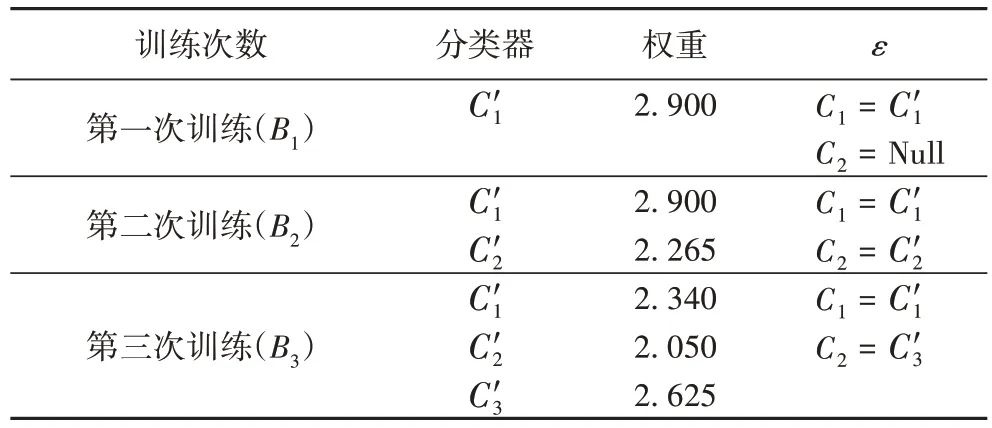
表2 分类器训练过程Tab 2 Classifier training process

3 实验与结果分析

本文实验硬件环境是Intel Core i5 1.4 GHz 8 GB RAM，软件环境是在线分析开源平台（Massive Online Analysis，MOA），所有实验均采用Java 语言实现。所有实验数据流全部由MOA 生成。本文使用提升在线学习集成（Boosting-like Online Learning Ensemble，BOLE）算法，基于适应性多样性的在线提升（Adaptable Diversity-based Online Boosting，ADOB）算法、LimAttClassifier（Combining Restricted Hoeffding Trees using Stacking）、OzaBoost（Oza and Russell’s online Boosting）、AUE2、OzaBoostAdwin（Boosting for evolving data streams using ADWIN）、LeveringBag（Leveraging Bagging）、OzaBag（Oza and Russell’s online Bagging）和自适应随机森林（Adaptive Random Forests，ARF）共9 种算法分别在10 个数据流上运行，实验结果在3.2 节详细介绍。

3.1 数据流

本文采用10 个数据流，它们均由MOA 生成，分别为SEA、LED（Light Emitting Diode）、径向基函数（Radial Basis Function，RBF）数据集、Waveform、Hyperplane1、Hyperplane2、Hyperplane3、Agrawal1、Agrawal2 和Agrawal3 数据集。

SEA 数据集由三个随机生成的属性

x

，

x

，

x

∈［0，10］来描述，并根据一个特定的方程来指定一个类标签；如果满足方程，则指定为一类，否则指定为另一类。LED 数据集的目标是预测七段式LED 显示屏上显示的数字，每个属性具有10%的反转机会，它具有74%的最佳贝叶斯分类。用于实验的发生器的特定配置产生24 个二进制属性，其中17 个无关。RBF 数据集为径向基函数生成器生成的数据集，其生成固定数量的随机质心，每个中心都有一个随机位置、一个标准偏差、分类标签和权重，所选的质心还确定实例的类标签。这有效地创建了围绕每个中心点且密度不同的实例的正态分布的超球体，它仅生成数字属性。Waveform 数据集，其任务的目标是区分三种不同的波形，每种波形是由两个或三个基波的组合生成的。最佳贝叶斯分类率已知为86%。该数据集有22 个属性，前21 个属性在实数范围内取值。Hyperplane 数据集共有11 个属性，前10 个为数值属性，共包含100 万个数据实例及2 个不同类标签。Agrawal 数据流共有10 个属性，共包含100 万个数据实例及2 个不同类标签。

其中Hyperplane2 和Hyperplane3 是通过修改Hyperplane1的参数得到的，同样的Agrawal2 和Agrawal3 是通过修改Agrawal1 数据流的参数生成。因EDW 在Agrawal 和Hyperplane 两个数据流中表现明显优于对比算法，因此在修改不同参数生成的数据流上实验可以更加证实算法适用此数据流及更复杂的数据流情况。Agrawal 和Hyperplane 数据流的参数修改情况如表3～4 所示。其中，Hyperplane 数据流中相同参数为InstanceRandomSeed：1；NumClasses：2；NumAtts：10；MagChange：0；SigmaPercentage：10。以上参数的修改都是经过大量的实验结果证明，修改对应的参数可以使数据流明显不同，使算法间的差异性可以明显比较。

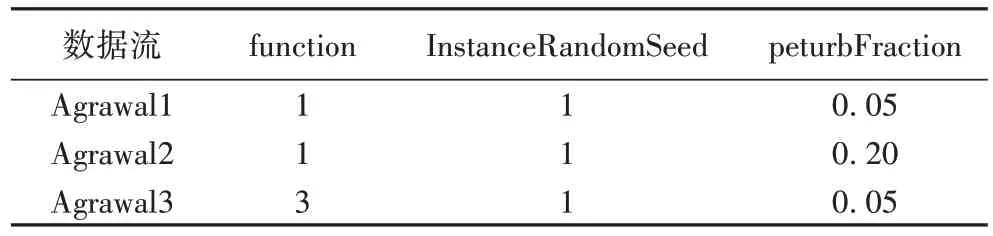
表3 Agrawal数据流参数Tab 3 Parameters of Agrawal data streams

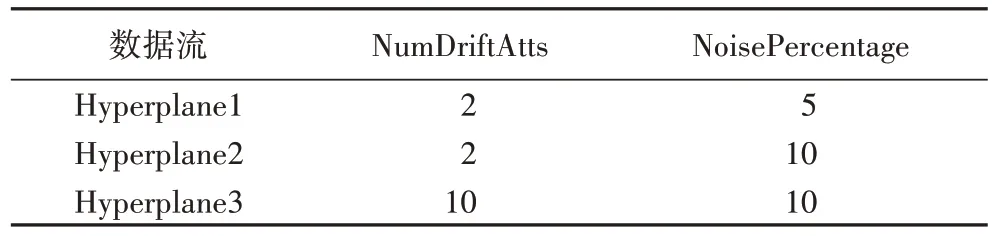
表4 Hyperplane数据流参数Tab 4 Parameters of Hyperplane data streams

3.2 实验

实验遵循MOA 中的先训练后测试的方法，测试和训练的数据流均由1 000 000 个数据实例组成。将本文算法与BOLE、ADOB、LimAttClassifier、OzaBoost、AUE2、OzaBoostAdwin、LeveringBag、OzaBag 和ARF 共10 种算法在不同的数据流中进行对比实验，本实验在多指标上对10 种算法进行了比较，包括块的大小对实验的影响、生成树的规模（叶子数、节点数以及树深度）、准确率以及运行时间。其中在Hyperplane1、Hyperplane2、Hyperplane3、Agrawal1、Agrawal2和Agrawal3 这6 个数据流对算法进行了生成树规模的比较。在 Hyperplane1、Hyperplane2、Hyperplane3、Agrawal1、Agrawal2、Agrawal3、SEA、LED、RBF 和Waveform10 个数据集上对算法在准确率和时间上的比较，其中在准确率的比较中，所有值均是100 万条实例每10 万条输出一次结果的均值。

3.2.1 块的大小对EDW的影响

因为EDW 是基于块的增量集成算法，在本节中研究块的大小对EDW 性能的影响，数据块是根据时间戳划分的大小相等的划分的块，当达到一定时间后实现了一个新的数据块，算法便会建立一定数量的候选分类器，与此同时更新后的数据样本也会在一定的时间内调整先前的集成成员，这样先前集成中的分类器就会随着时间不断扩大，通常认为最新的数据块样本最新的概念，所以认为这种更新机制可以迅速对概念漂移作出反应。

块的大小很可能影响到块集成的分类性能，块过大将引入过多的概念漂移，但使用较小的块也会限制分类器中的数据流信息。在最新数据块上建立候选分类器的块集成可以分为两类，一种是由数据块中的样本数决定训练集的大小，其将所有的集成成员都建立在候选块上，另一种是使用最新的数据块来训练候选分类器。本节的实验目的是验证块的大小是否会影响EDW 的准确率，实验结果如表5 所示，在上述的10 个数据集中对EDW 进行了实验，数据块大小

d

分别设置为500、800、100、1 500 和2 000，每个数据集中的最优结果用黑体加粗表示。从表5 中可以看出，在不同的

d

下，EDW 的性能没有太大的差异，EDW 的准确率不受块的大小的影响。在之后比较实验中，块的大小设置为一个固定的值，确保后续实验的准确性。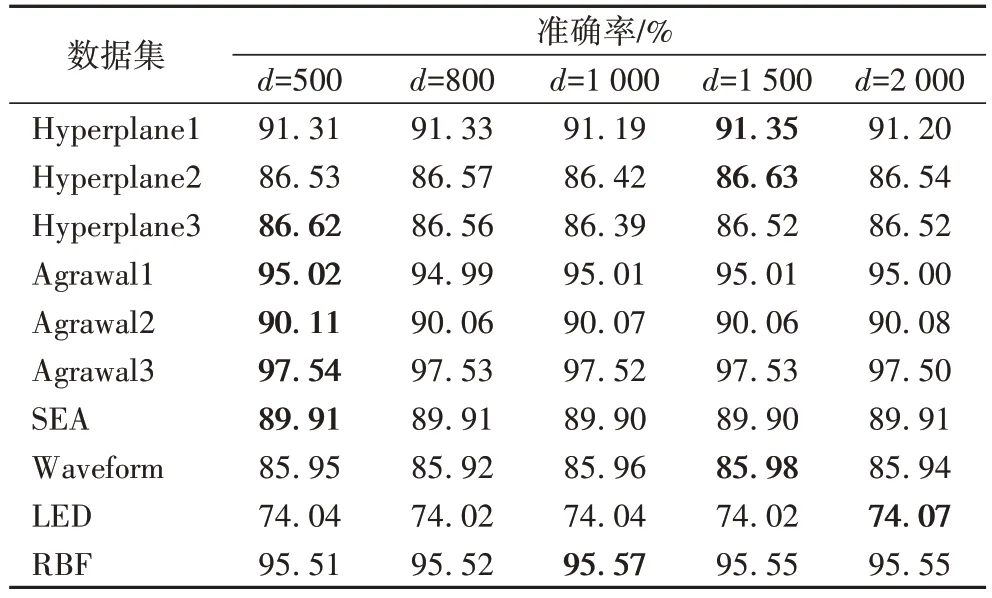

表5 各数据集下不同块大小EDW的准确率Tab 5 EDW accuracies of different block sizes on each dataset

3.2.2 生成树规模对比实验

本节将对提出的EDW 以及8 个对比算法在6 个数据集上进行生成树规模的对比，选择这6 个数据集做生成树规模对比实验是因为经过大量的实验后，本文算法在这些数据集上表现良好，然后在此基础上进行空间上生成树的比较，观察其效果。实验结果如表6 所示，其中最优的数据已经用粗体显示。

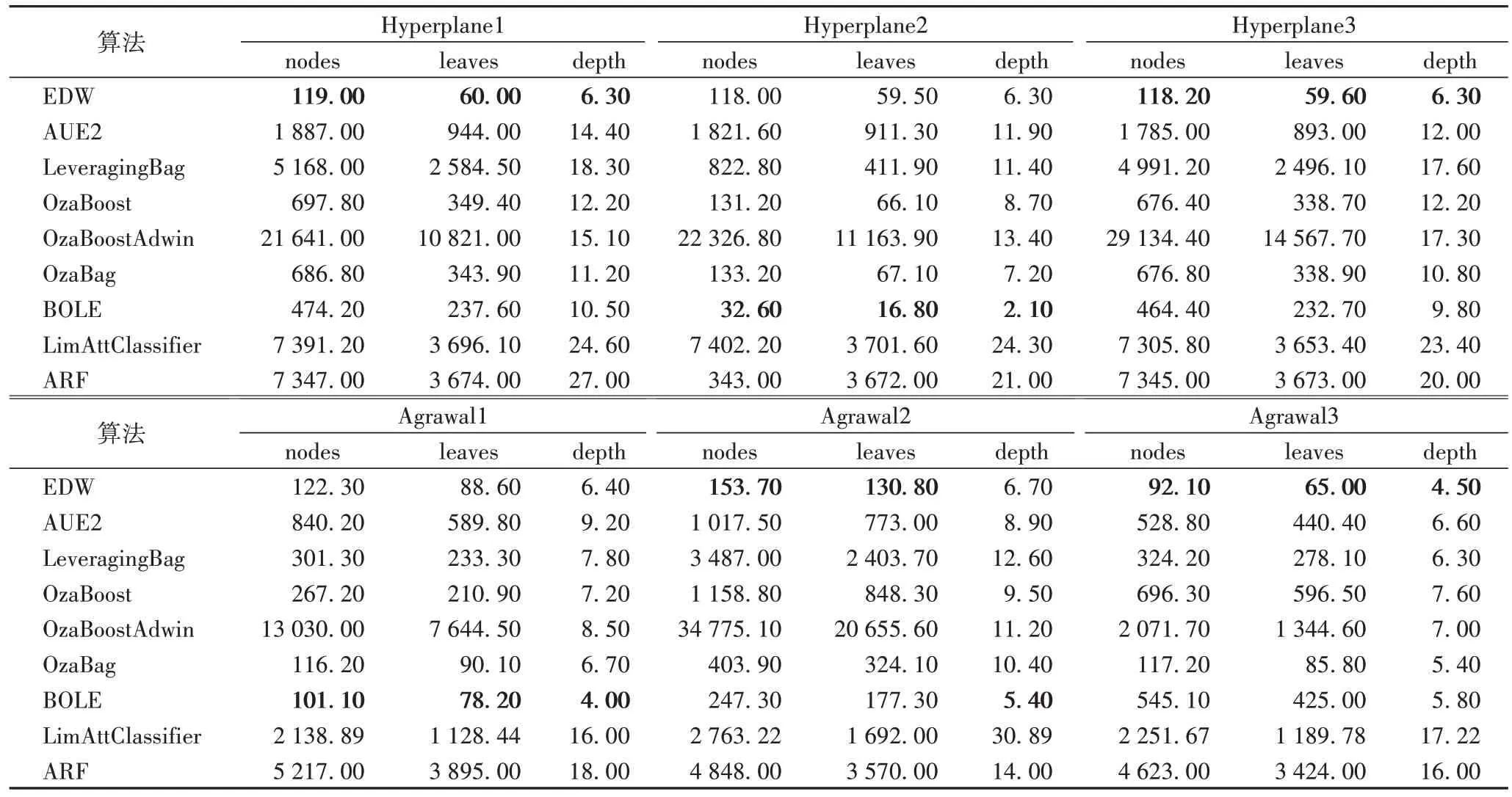
表6 生成树规模比较Tab 6 Spanning tree scale comparison

由表6 可以得知，在Hyperplane1 和Hyperplane3 数据集中与其他几个算法相比，EDW 的生成的节点数、叶子数以及树的深度均是最少的。以Hyperplane3 为例，与LimAttClassifier、ARF 和OzaBoostAdwin 相比，节点数分别减少 了7 187.6、7 226.8 和29 016.2，分别减少了98.3%、98.4%和99.6%；从叶子数观察，以相同的算法进行举例，叶子数分别减少了3 593.8、3 613.4 和14 508.1，分别减少了98.4%、98.38%和99.6%；同样，本文算法在树的深度层面上分别降低了17.1 层、13.7 层和11 层，分别减少了73.1%、69%和63.6%。与对比算法相比，EDW 的树规模数据很有优势。

在Agrawal 数据集及其变体的实验下可以看到，本文算法在Agrawal2 和Agrawal3 数据集上与其他对比算法相比取得了最好的效果。以Agrawal2 数据集举例，与OzaBoostAdwin、LimAttClassifier 和ARF 三个算法相比，节点数分别减少了34 621.4、2 609.52 和4 694.3，分别减少了99.6%、94.4%和99.6%；从叶子数观察，以相同的算法进行举例，叶子数分别减少了20 524.8、1 561.2 和3 439.2，分别减少了99.4%、92.3%和996.3%；同样，本文算法在树的深度层面上分别降低了4.5 层、24.19 层和7.3 层，分别减少了40.2%、78.1%和52.1%。EDW 减少了相当多的节点数与叶子数，树深度的效果也很可观；即使在Agrawal1 数据集下，树规模的数据与最优数据相比稍有落后，但是相差甚微，纵观所有算法的树规模数据还是很有优势的。

3.2.3 算法准确率对比实验

本节将对提出的EDW 以及9 个对比算法在10 个数据集上进行准确率和时间上的对比，如表7～8 所示。在准确率方面，EDW 在除Hyperplane2、Hyperplane3 和LED 三个数据集外准确率均优于其他9 个对比算法，相较于ADOB 算法平均提高了25%左右。在Hyperplane2、Hyperplane3 和LED 这三个数据集上也仅与对比算法的最优准确率相差1%～2%。在Agrawal1 数据集中EDW 高于ARF 算法近20%的准确率。在LED 数据集中EDW 相较于ARF 算法有着45.52%的优势。总的来说，EDW 虽仅在7 个数据集上取得最优准确率，但是在其他3 个数据集与其他对比算法的最优准确率相差甚微，这在空间大幅减少的前提下，是一个不错的表现。

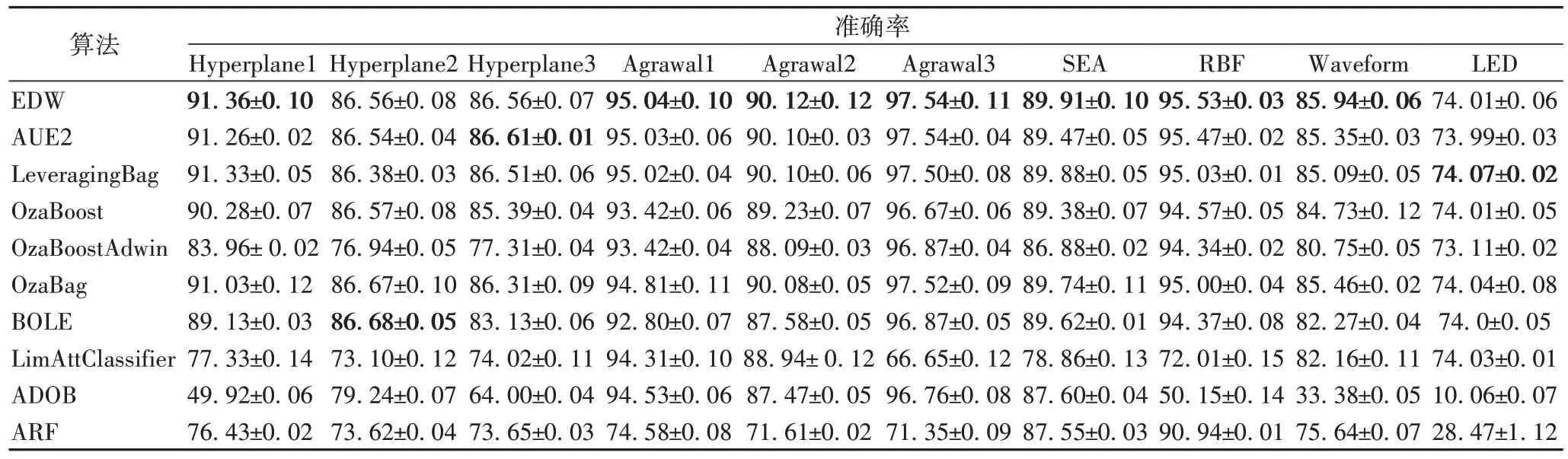
表7 各算法准确率对比 单位：%Tab 7 Accuracy comparison of different algorithms unit：%

如表8 所示，在时间对比实验中，虽然ARF 算法运行的时间最短，但是因为其不是集成算法，对于不断变化的数据流准确率也很低，所以在这里不与它进行比较。除了ARF算法以外的算法中EDW 在10 个数据集中均取得了不错的效果，虽然在其中一些数据集中EDW 中不是使用最短的时间，这是因为在对数据分类的过程中该算法对基分类器重新计算权重等过程中耗费了一些时间，但是在提高了准确率和减少空间占比的前提下，处理1 000 000 条数据的数据集中与用时更少的对比算法相比仅多出几秒甚至零点几秒是可以接受的结果。

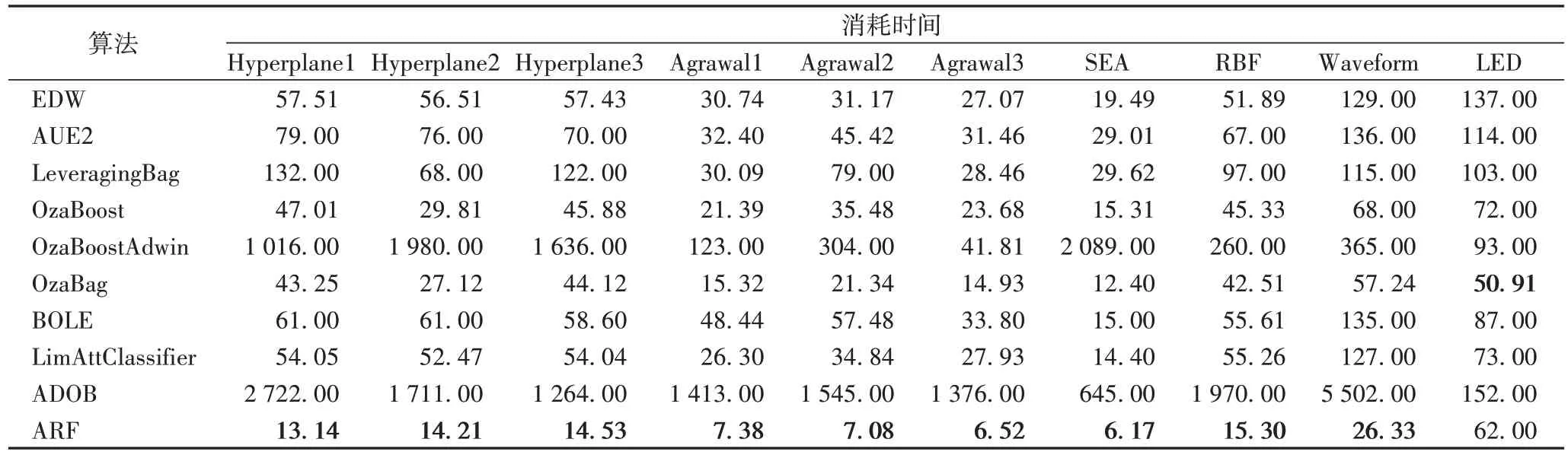
表8 各算法时间代价对比 单位：sTab.8 Time cost comparison of different algorithms unit：s

因为本文算法在Hyperplane 和Agrawal 数据集中取得了很好的准确率，这也是在之前集中研究这两个数据集以及其对参数进行修改后的变体进行实验的原因。生成树规模对比实验是在上一个实验算法准确率相差不大的情况下进行的，因为ADOB 算法在实验中的几个数据集上准确率都不是太理想，所以在进行生成树规模的实验中就没有考虑该算法。图2 代表了在同样两个数据集下生成树的节点数和叶子数，因为OzaBoostAdwin 产生了极大的节点数和叶子数，所以扩大了整个柱状图的比例，导致OzaBoost、OzaBag 和BOLE的实验数据在图中看似与本文提出的算法相差不多，但实际在数量上仍然相差5 到7 倍。所以可以看出在这两个数据集上，EDW 生成的节点数和叶子数极少，这在有限的内存中节省了大量空间。

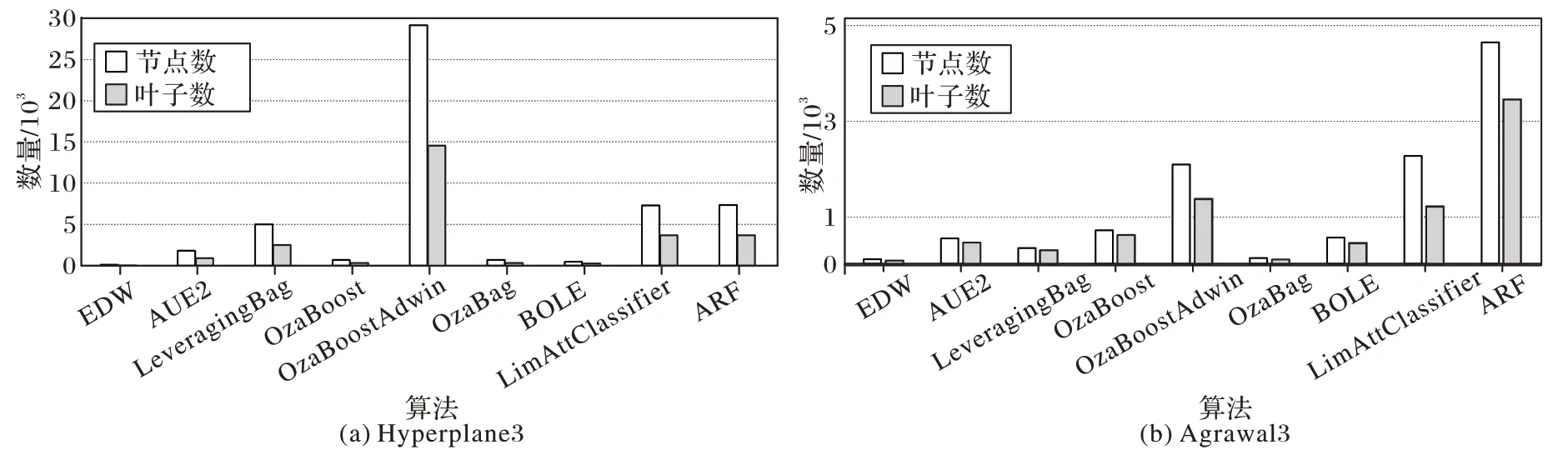
图2 各算法数据流生成树的节点数和叶子数对比Fig.2 Comparison of nodes and leaves of data stream spanning trees in different algorithms

图3 代表Hyperplane3 和Agrawal3 两个数据集下的生成树的深度对比，在这两个数据集中可以清晰地看到本文提出的EDW 在树的深度上始终保持着最小的深度，与LimAttClassifier 算法相差了十几层树深度，在产生大量叶子数和节点数的情况，减少树深度可以减小很多内存的使用。

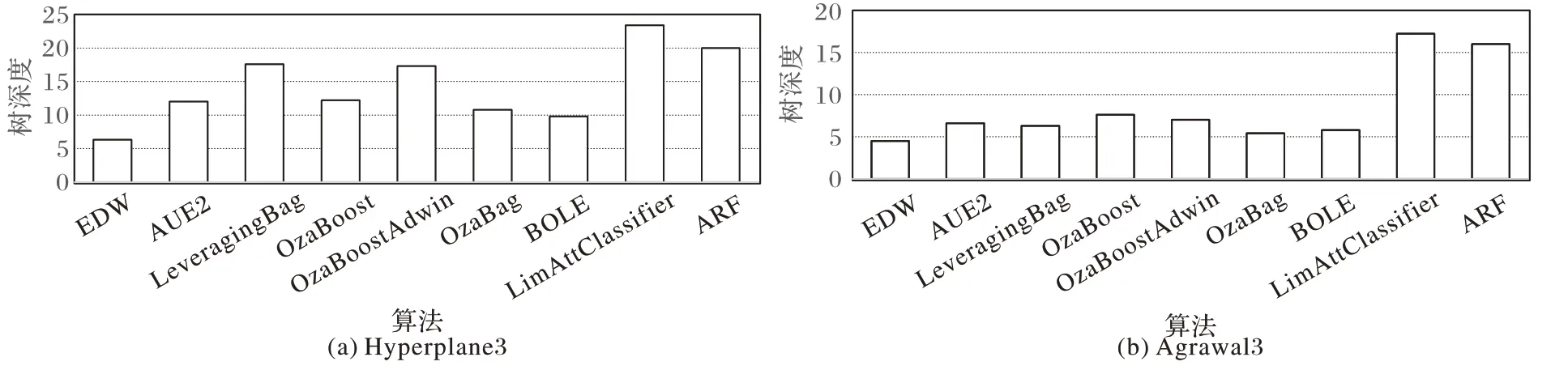
图3 各算法数据流生成树的深度对比Fig.3 Comparison of depth of data stream spanning trees in different algorithms

图4 为EDW 以及其他8 个对比算法在100 万条的数据集下的精度绘制了折线图，代表了各种算法在两个数据集下准确率对比。可以看到在两个数据集上，本文算法均在最优的范围内，其中在图4（b）中，为了更好地展示几个较高准确率的算法中的差异，LimAttClassifier 和ARF 算法因为准确率过低，为66.65%与77.35%，缺少可比性，就没有显示在图中。从这两张图中可以得出，EDW 在大幅减小树规模的同时，准确率仍然保持在最优范围内，是一个效果较好的集成算法。

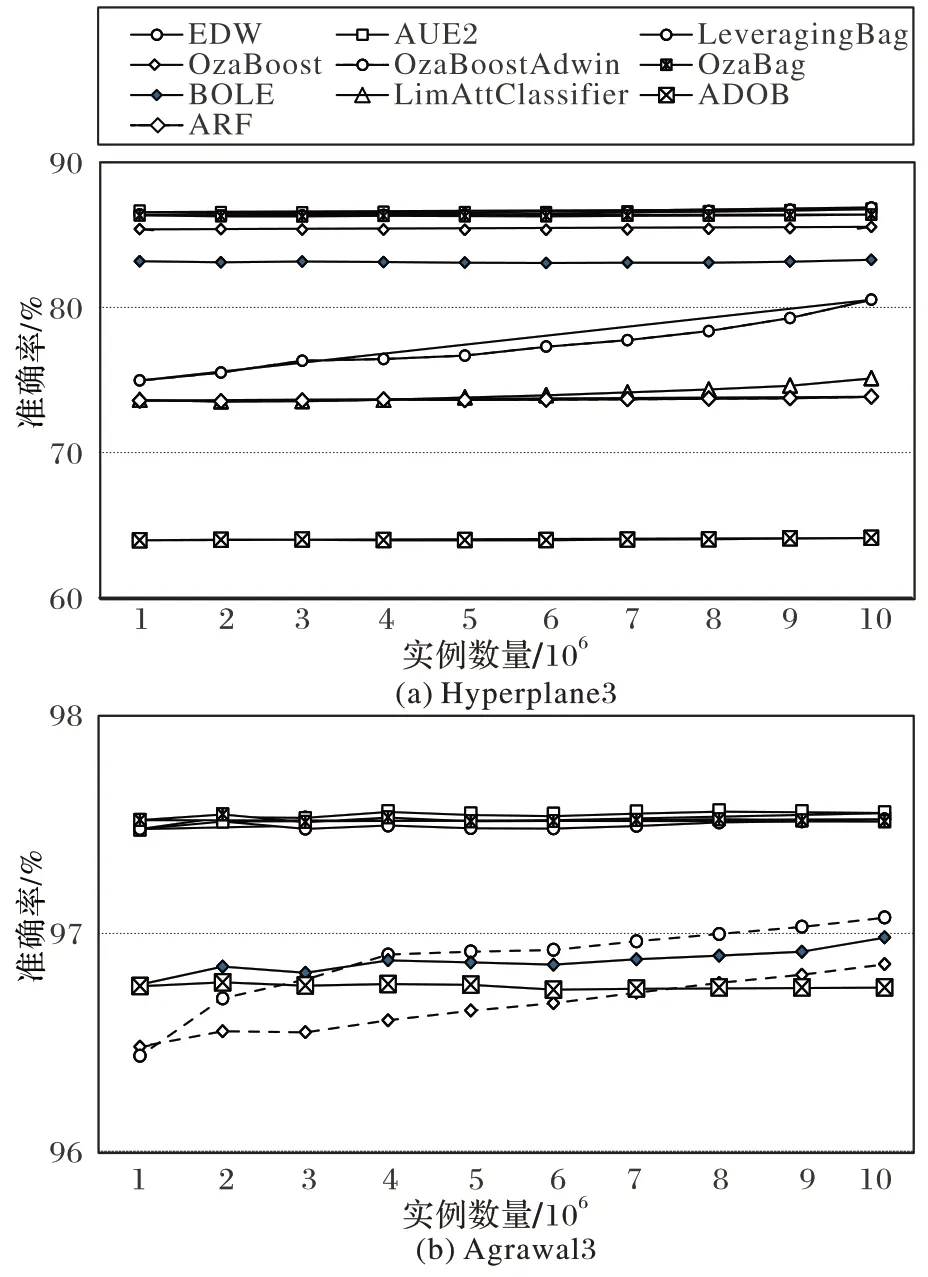
图4 各算法数据流准确率对比Fig.4 Comparison of accuracy of data streams for different algorithms

4 结语

本文提出了一个可以计算基分类器的权重的算法，调节分类器的权重对其进行一个合理的选择，根据在最新数据块中对样本数据估计其预期的预测误差，评估每个基分类器的性能。同时本文使用基于泰勒定理和正态分布的性质的决策树作为基分类器，使其可以根据有限的数据样本进行分割并且辨别当前节点的最佳属性其是否也是整个数据流的最佳属性，提出了一种基于动态加权函数的集成分类算法。实验结果表明，本文提出的算法的性能不受块的大小影响，大幅地减小了生成树的规模，准确率方面效果较好，也能很好地适应带有概念漂移和噪声的数据流。未来将对该算法的运行时间上进行进一步的研究，尽可能地减少不必要的计算，提升计算效率，更好地节省运算时间。