改进的联邦加权平均算法

罗长银，王君宇，陈学斌*，马春地，张淑芬

（1.华北理工大学理学院，河北唐山 063210；2.河北省数据科学与应用重点实验室（华北理工大学），河北唐山 063210；3.唐山市数据科学重点实验室（华北理工大学），河北唐山 063210）

0 引言

自谷歌于2016 年提出联邦学习（Federated Learning，FL）以来，联邦学习受到国内外专家学者的广泛关注，因具有保护隐私数据的潜力，被广泛应用于多个领域。

联邦学习的训练数据是基于各个数据源本地的数据进行训练的，不需要收集、存储数据到云端和整合多方数据，这种方法大幅降低了敏感信息泄露的风险。文献［9］中，使用区块链来存储各时间段内训练的模型参数，降低了在存储方面的成本，同时也降低了因模型参数还原原始数据的风险。但因联邦学习的训练数据来源于不同数据源，训练数据并不能满足独立分布和训练数量一致这两个能影响联邦模型的条件。若数据源的训练数据分布不同，那么整合多方的子模型成为巨大的难题。

在联邦学习框架的应用中，最常见的算法是联邦平均（Federal Average，FedAvg）算法。文献［17］从数据质量的角度对原有的FedAvg 算法进行改进，考虑到数据源之间数据质量的差异导致权重的不合理分配问题，文献［17］使用层次分析法对权重进行改进；但层次分析法中比较矩阵的数值由人为确定，存在不可靠因素。因此，本文采用预训练机制来计算各客户端的精度，将其作为各客户端的质量，并结合客户端数据量的大小，重新计算全局模型中权重更新的方法，能够给出相对合理的权重分配方案。实验结果表明，改进的联邦加权平均算法与传统联邦平均算法相比准确率有所提升。

1 改进的联邦加权平均算法

1.1 联邦学习

联邦学习（FL）是一种隐私保护算法，是算法优化实现路径和保护数据安全的前提下解决数据孤岛问题的解决方案。具体实现过程为：对多个参与方在本地私有数据上进行模型训练，然后将不同的模型参数上传到云端进行整合和更新，之后将更新的参数发送至各参与方。整个过程私有数据不出本地，既保证了数据隐私，又解决了各参与方“数据孤岛”的困境。根据联邦学习的实现过程使得FL 具有保护隐私和本地数据安全的优势。

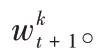
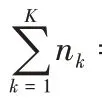
1.2 改进的联邦加权平均算法

联邦加权平均算法是在原有的联邦平均算法的基础上添加了数据质量的权重，其计算的核心是将各客户端的训练样本分为两部分：一部分作为初始全局模型的训练样本，在客户端的训练样本上进行训练；另一部分为预测试样本，在训练完成之后，计算其模型正确率。正确率

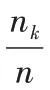
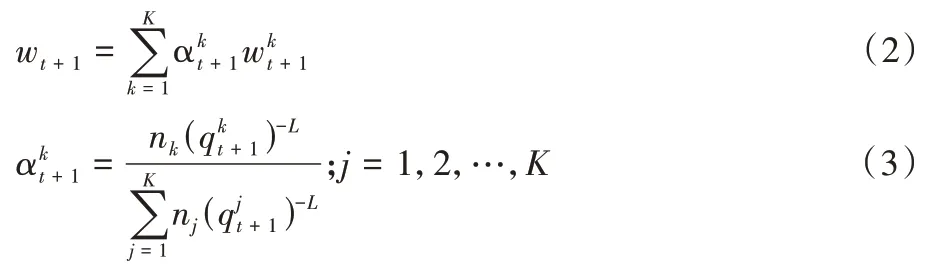
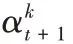
q

的计算公式为：

其中：

C

表示第

t

个客户端建立的模型在与测试样本上预测正确的样本数；

X

表示预测试样本数。

1.3 算法的流程

步骤1 各客户端将数据样本按照一定的比例划分为训练样本和测试样本；

步骤2 各客户端将训练样本按照比例划分为预训练样本和预测试样本；

步骤3 中心服务器使用由RSA（Rivest-Shamir-Adleman）加密算法产生的公钥对随机森林、朴素贝叶斯、神经网络、决策树4 种初始全局模型加密并传输至客户端；

步骤4 客户端使用私钥解密后，获取4 种初始全局模型；

步骤5 各客户端使用不同类型的初始全局模型在预训练样本上进行训练，获得本地模型；

步骤6 各客户端将本地模型在预测试样本上进行预测，获取预测正确的样本数

C

；

步骤7 客户端使用式（4）来计算其数据的质量；

步骤8 从客户端的数据数量与质量两方面来使用式（3）计算出客户端的权重；

步骤9 将客户端上使用4 种初始全局模型训练的本地模型与步骤7 计算的客户端的权重相乘，并以此获取更新的全局模型；

步骤10 不断迭代优化其客户端的权重，直到达到停止条件。

1.4 算法性能

本文采用预训练的方法对各客户端的权重进行优化，并与联邦平均算法进行结合，从而获取各客户端的权重变化。

1.4.1 算法的复杂度分析

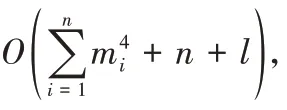
1.4.2 算法的安全性分析

本文算法采用预训练的方法，在数据层面上，因采用联邦平均算法的框架结构，其训练所用的数据仅在本地进行训练，满足模型找数据的本质要求，使数据在使用方面的安全性得到提升；在模型层面上，因采用非对称加密算法对本地模型与初始全局模型进行分发与整合，使模型在传输过程中的安全性得到提升。

2 实验与结果分析

2.1 实验设置

实验硬件环境为：Inter Core i5-4200M CPU 2.50 GHz 处理器，内存8 GB；操作系统为Windows10。

2.2 实验数据分析

实验数据采用UCI（University of California-Irvine）数据集中 的digits数据集、recognition 数据集、segment 数据集、segmentation 数据集与telescope 数据集进行实验。表1 列出了实验中所使用的5 组数据集的基本信息。对于每个数据集，重复进行了100 次实验，用100 次准确度的均值作为准确率，将准确率与方差作为算法性能差异比较的依据。

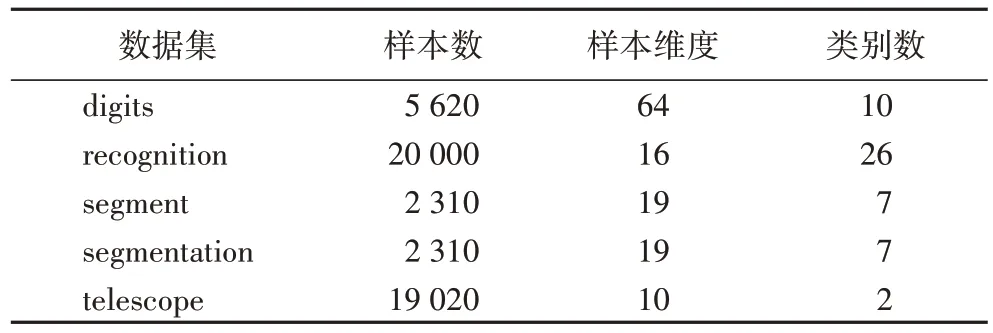
表1 实验所使用的数据集Tab 1 Datasets used for experiment

为充分模拟多源数据的特点，将各数据集随机划分，其中包括均分与非均分两种情况。均分的情况是：将各数据集的数据随机划分100 次且每次都均等划分，同时将初始全局模型在均等随机划分100 次的数据上进行训练，所获得的准确度的均值来作为准确率，使用方差来衡量模型的收敛情况。非均分的情况采取相同的方法。

实验分为两部分：第一部分是模型权重中参数的调整与计算。首先客户端将自身的数据划分为训练样本与测试样本，并将训练样本再次划分为预训练样本与预测试样本，其次将随机森林、朴素贝叶斯、神经网络、决策树在预训练样本上训练的得分作为该客户端的数据质量，最后根据客户端的数据数量与质量综合给出客户端的权重。第二部分是可信第三方使用公钥对随机森林、朴素贝叶斯、神经网络、决策树、加密并传输至客户端，客户端使用私钥解密后，获取4 种初始全局模型，且使用4 种初始全局模型分别进行训练，客户端获取本地模型，使用公钥对客户端上的本地模型进行加密并传输至可信第三方，可信第三方将多个本地模型与权重相乘获取更新的全局模型，并不断优化迭代，直到更新的全局模型的准确率满足停止条件。

第一部分：各客户端（

k

=1，2，3）将自身的训练样本划分为预训练样本与预测试样本，并使用不同的初始全局模型在预训练样本上的得分作为该客户端的数据质量，同时对式（3）中的

L

取值为-10。对数据进行均等划分和非均等划分两种情况，表2 为不同的初始全局模型在均等情况下预测试样本的得分情况；表3 为不同的初始全局模型在非均等情况下预测试样本的得分情况。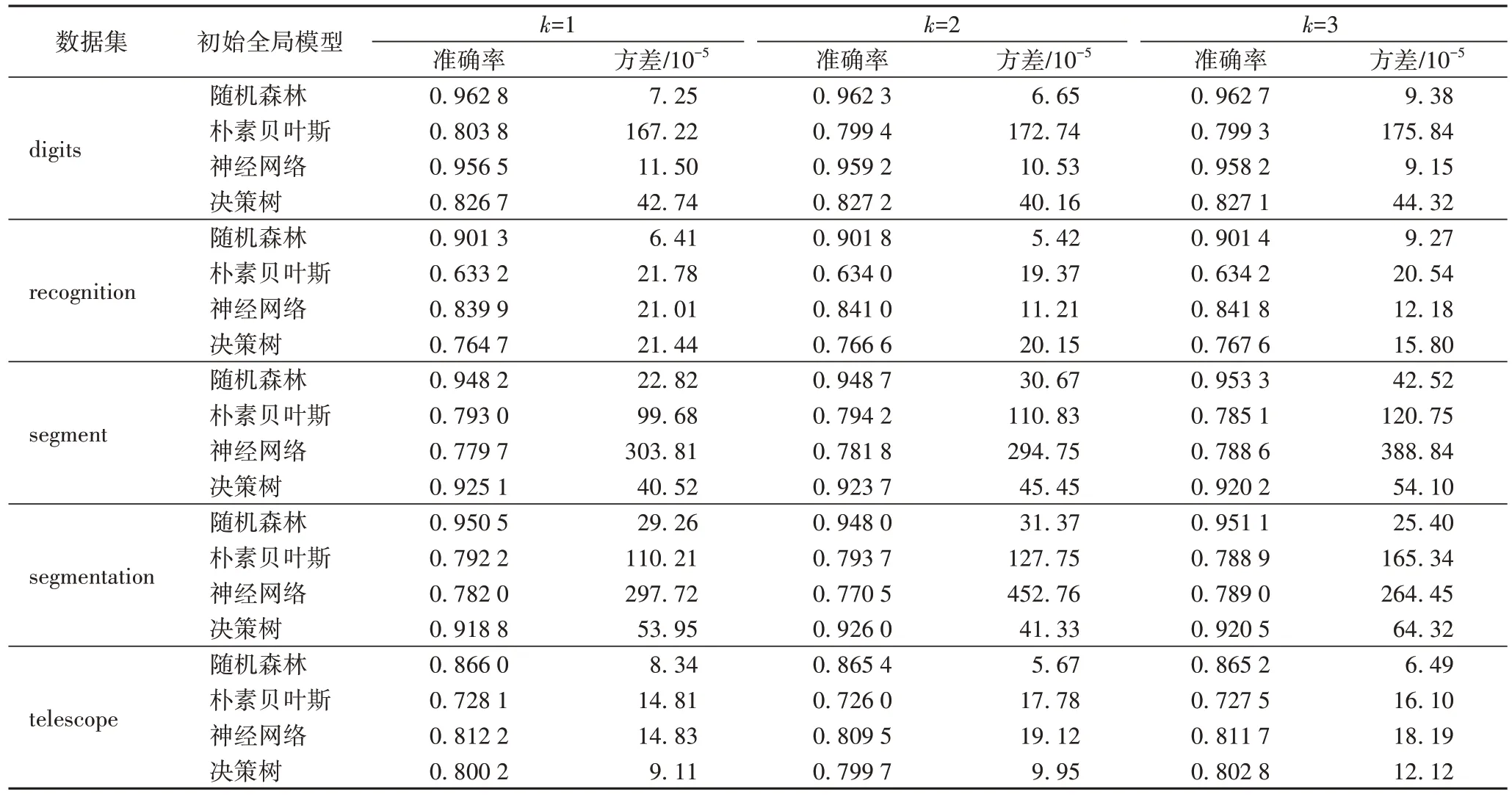

表2 不同初始全局模型在不同数据集均等分割的预测试样本上的准确率及方差Tab 2 Accuracy and variance of different initial global models on pre-test samples of different equal divided datasets

从表2 中可以看到将各数据集分别进行均等分割，使用不同的初始全局模型在均等分割的数据上进行训练，不同的初始全局模型在不同的客户端的预训练样本上进行训练，其建立的模型在预测试样本上的得分情况，即各客户端上数据质量的情况。当数据集选用digits 时，4 种初始全局模型在各客户端上的数据为均等情况下的训练得分，其中：随机森林在预测试样本上准确率在96.23%以上，同时方差最大的为9.38 × 10；朴素贝叶斯在预测试样本上准确率在79.94%以上，方差最大的为167.22 × 10；神经网络在预测试样本上准确率在95.65%以上，方差最大的为11.5 × 10；决策树在预测试样本上准确率在82.67%以上，方差最大的为44.32 ×10。当数据集选用recognition 时，4 种初始全局模型在各客户端上的数据为均等情况下的训练得分，其中：随机森林在预测试样本上准确率在90.13%以上，同时方差最大的为9.27 × 10；朴素贝叶斯在预测试样本上准确率在63.32%以上，方差最大的为21.78 × 10；神经网络在预测试样本上准确率在83.99%以上，方差最大的为21.01 × 10；决策树在预测试样本上准确率在76.47%以上，方差最大的为21.44 ×10。当数据集选用segment 时，4 种初始全局模型在各客户端上的数据为均等情况下的训练得分，其中随机森林在预测试样本上准确率在94.82%以上，同时方差最大的为45.52 ×10；朴素贝叶斯在预测试样本上准确率在78.51%以上，方差最大的为120.75 × 10；神经网络在预测试样本上准确率在77.97%以上，方差最大的为388.84 × 10；决策树在预测试样本上准确率在92.02% 以上，方差最大的为54.10 × 10。当数据集选用segmentation 时，4 种初始全局模型在各客户端上的数据为均等情况下的训练得分，其中：随机森林在预测试样本上准确率在94.81%以上，同时方差最大的为31.37 × 10；朴素贝叶斯在预测试样本上准确率在78.89%以上，方差最大的为165.34 × 10；神经网络在预测试样本上准确率在77.05%以上，方差最大的为452.76 ×10；决策树在预测试样本上准确率在91.88%以上，方差最大的为64.32 × 10。当数据集选用telescope 时，4 种初始全局模型在各客户端上的数据为均等情况下的训练得分，其中：随机森林在预测试样本上准确率在86.52%以上，同时方差最大的为8.34 × 10；朴素贝叶斯在预测试样本上准确率在72.60%以上，方差最大的为17.78 × 10；神经网络在预测试样本上准确率在80.95%以上，方差最大的为19.12 ×10；决策树在预测试样本上准确率在79.97%以上，方差最大的为12.12 × 10。

将各数据集分别进行非均等分割，使用不同的初始全局模型在非均等分割的数据上进行训练，不同的初始全局模型在不同客户端的预训练样本上进行训练，其建立的模型在预测试样本上的得分情况，即各客户端上数据质量的情况如表3 所示。

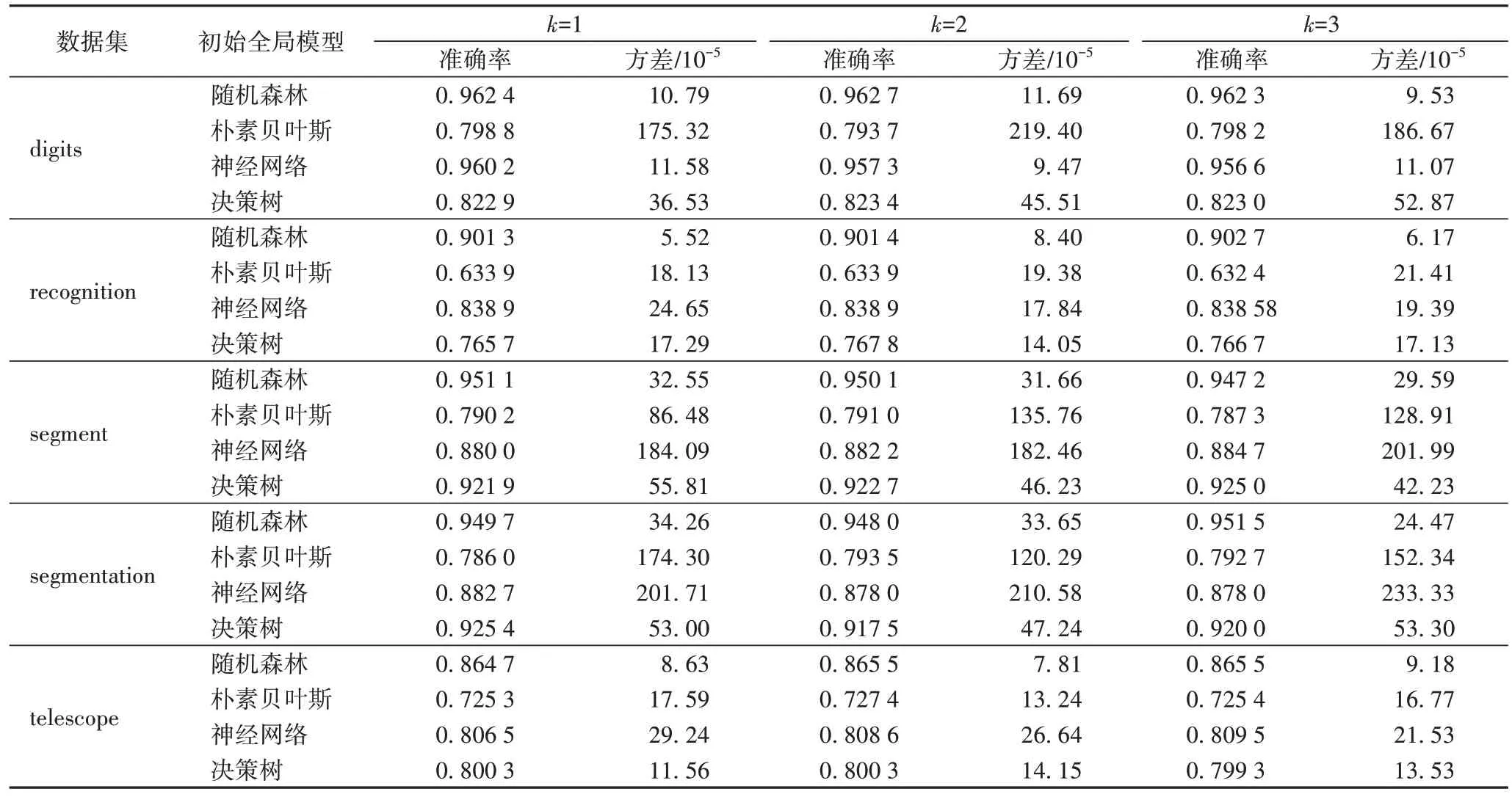
表3 不同初始全局模型在不同数据集非均等分割的预测试样本上的准确率及方差情况Tab 3 Accuracy and variance of different initial global models on pre-test samples of different unequal divided datasets

第二部分：各客户端在预训练样本上训练得到本地模型，将本地模型使用第一部分所计算的权重进行汇总，建立更新的全局模型。表4 为加权联邦平均算法和传统未加权联邦平均算法所得到的更新的全局模型的准确率的情况。

从表4 中可以很明显地得到数据在均分与非均分的情况下，不同初始全局模型在各客户端的数据上进行训练的情况，同时使用准确度均值与方差来衡量模型的性能。

传统联邦平均算法是可信第三方将4 种初始全局模型分别传输至客户端，客户端进行训练后得到本地模型，再采用平均法整合多个数据源的本地模型，汇总成更新的全局模型。从表4 中可以看出，无论是加权联邦平均算法还是传统的联邦平均算法，其随机森林的准确率均高于其他三种模型的准确率，且方差最小。同时当数据为非均分情况下建立的模型准确率都大于均分情况下的建立的模型的准确率。与传统联邦平均算法相比，改进的联邦加权平均算法的准确率最高分别提升了1.59%和1.24%。

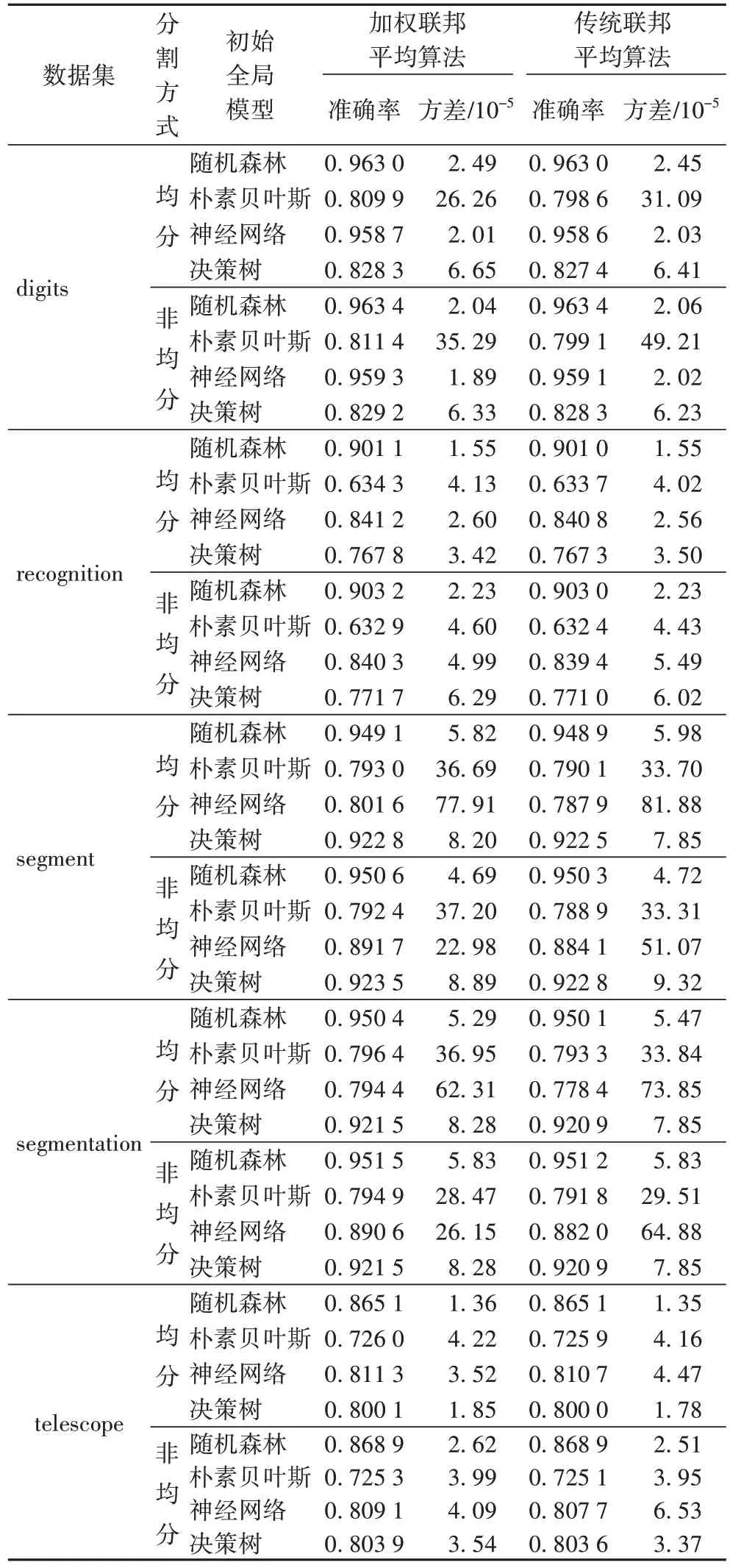
表4 加权联邦平均算法和传统联邦平均算法准确率比较Tab 4 Accuracy comparison of weighted federated average algorithm and traditional federated average algorithm

传统的多源数据处理方法整合多方数据存放在数据中心，再进行训练而得到全局模型。表5 为传统的多源数据处理方法在digits 数据集、recognition 数据集、segment 数据集、segmentation 数据集与telescope 数据集上模型训练的情况。

从表5 中可以得到使用传统多源数据处理技术建立的模型的准确率的情况，同时表格中的数据为十折交叉得到的数值，可以很明显看出，在digits 数据集、recognition 数据集、segment数据集、segmentation数据集与telescope 数据集中随机森林的准确率最高。

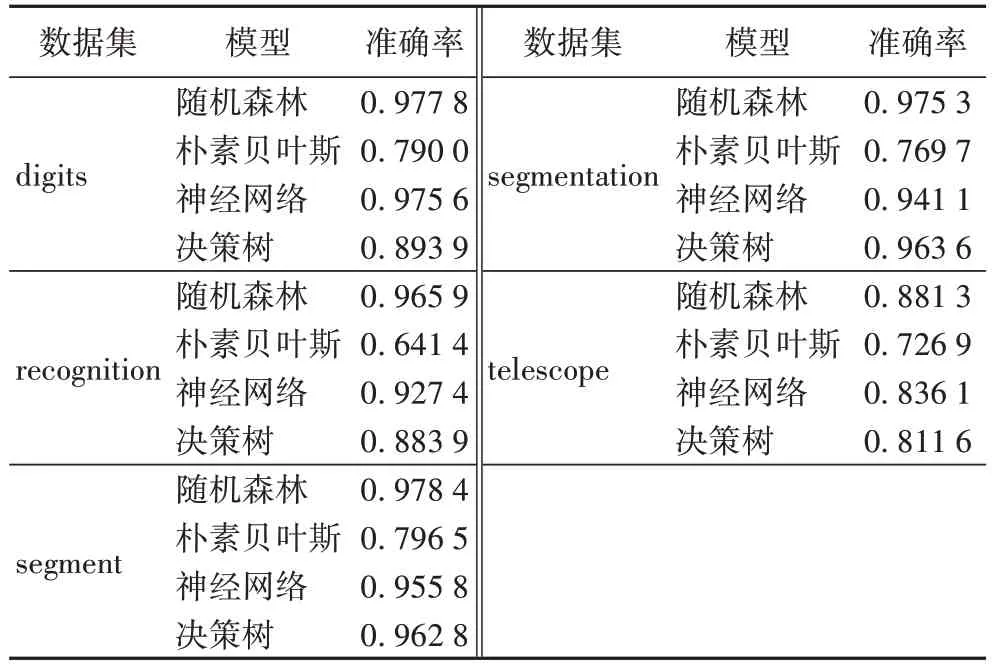
表5 传统的多源数据处理方法建立的模型准确率Tab 5 Accuracies of models established by traditional multi-source data processing method

文献［17］采用层次分析法对联邦平均算法进行改进，表6 为根据层次分析法改进的联邦平均算法建立的模型的准确率的情况。

从表6 中可以看出，改进模型在digits 数据集、recognition数据集、segment 数据集、segmentation 数据集与telescope 数据集中随机森林的准确率最高。将本文算法的准确率最优值与基于层次分析法改进的联邦平均算法相比，本文算法在digits 数据集中，随机森林的准确率降低了1.13%，朴素贝叶斯的准确率提升了8.06%，神经网络的准确率降低了1.13%，决策树的准确率降低了5.75%；在recognition 数据集中，随机森林的准确率降低了3.94%，朴素贝叶斯的准确率提升了5.58%，神经网络的准确率提升了3.76%，决策树的准确率提升了13.07%；在segment 数据集中，随机森林的准确率降低了1.59%，朴素贝叶斯的准确率提升了2.48%，神经网络的准确率提升了3.78%，决策树的准确率降低了1.47%；在segmentation 数据集中，随机森林的准确率降低了1.31%，朴素贝叶斯的准确率提升了3.42%，神经网络的准确率提升了0.94%，决策树的准确率降低了1.63%；在telescope 数据集中，随机森林的准确率提升了0.31%，朴素贝叶斯的准确率降低了0.51%，神经网络的准确率提升了25.55%，决策树的准确率降低了2.96%。

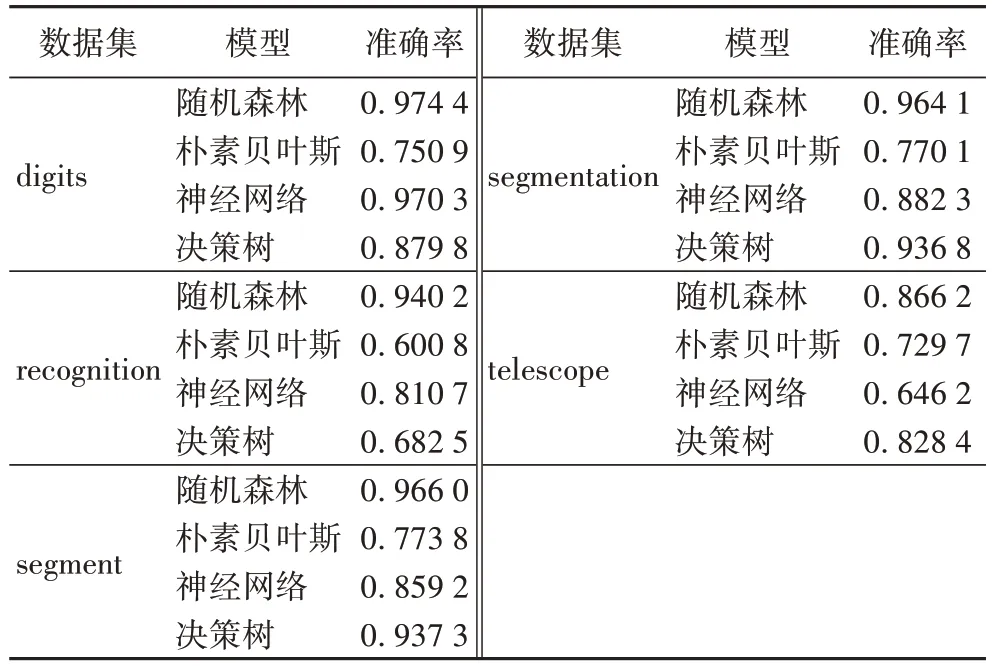
表6 基于层次分析法改进的联邦平均算法建立的模型准确率Tab 6 Accuracies of models established by the improved federated average algorithm based on analytic hierarchy process

2.3 实验小结

该算法将训练样本划分为预训练样本与预测试样本，且将在预训练样本上建立的本地模型在预测试样本得到的分数作为各客户端的数据质量，并计算出各客户端的权重；可信第三方将4 种初始全局模型加密传输至客户端，客户端解密后并进行训练，获取本地模型，客户端将本地模型传输至可信第三方，可信第三方将根据数据质量计算得到的权重来整合多个本地模型。对于digits 数据集、recognition 数据集、segment 数据集、segmentation 数据集与telescope 数据集而言，不论数据是否为均分，当初始全局模型为随机森林、朴素贝叶斯、神经网络和决策树时，与传统联邦平均算法相比，其准确率均有所提升。与传统多源数据处理技术相比，虽然准确率略有下降，但数据的安全性得到了提升。

3 结语

本文在消除主观因素的情况下，从数据质量的角度对联邦平均算法进行优化，将训练样本划分为预训练样本与预测试样本，将初始全局模型在预训练样本上训练，所建立的模型在预测试样本上进行预测所得到的分数作为其数据质量，并计算出相应的权重；同时采用加密传输的方式将不同模型类型传输至各数据源，各数据源在训练后并进行整合，获取更新后的全局模型，在提升模型准确率的同时兼顾了模型与多源数据的安全性。未来的工作中，将差分隐私应用到该算法中，进一步提升数据的隐私性和模型的可用性、安全性。