基于国内宽带VLBI2010系统及iGMAS的UT1/ΔLOD数据融合方法
李西顺, 吴元伟, 姚 当, 刘 佳, 马浪明, 杨旭海, 张首刚
(1. 中国科学院国家授时中心, 陕西 西安 710600; 2. 中国科学院大学电子电气与通信工程学院,北京 100049; 3. 中国科学院精密导航定位与定时技术重点实验室, 陕西 西安 710600;4. 中国科学院时间频率基准重点实验室, 陕西 西安 710600)
0 引 言
世界时(universal time, UT1)是以地球自转定义的时间尺度,是构成标准时间,即协调UT1(UT1 coordinated, UTC)的重要组成部分。UT1与极移、章动改正项组成了地球定向参数(earth orientation parameter, EOP),关于需要在地球坐标和天球坐标之间建立坐标变换的应用,UT1都必不可少,UT1数据服务是卫星导航、深空探测等领域所必须的基础服务。
当前权威的UT1产品由国际地球自转服务组织(International Earth Rotation Service, IERS)提供。该产品由多种空间大地测量技术综合得到。在这些技术中甚长基线干涉测量(very long baseline interferometry, VLBI)技术和全球卫星导航定位系统(global navigation satellite system, GNSS)技术发挥着重要作用。其中VLBI技术不用考虑动力学因素效应,是仅有的能够做到监测UT1变化的空间大地测量技术,也是目前唯一能够解算全部地球定向参数的空间技术。VLBI技术因具有极高的测角精度和长期的稳定性,在解算EOP 和维持地球及天球参考框架方面发挥着举足轻重的作用;但由于成本原因,尚未进行长期的连续观测,导致其观测频度不足。GNSS 技术因观测站遍布全球,可实现不间断的连续观测,通过解算可得到日长变化ΔLOD、极移,但GNSS解算的ΔLOD受制于轨道升交点进动问题,长期稳定性有待提高。将上述两种空间技术融合解算可以有效解决VLBI 技术观测UT1频率不足以及GNSS技术解算ΔLOD长期稳定性上的不足,从而得到更连续、精度更高的UT1产品。
本文使用仿真与实测相结合的方法,首先通过马尔可夫链蒙特卡罗(Markov chain Monte Carlo, MCMC)模拟仿真了UT1随机误差、时间间隔、系统偏差对于融合精度的影响以及权比的依赖关系。然后将国内首套宽带VLBI2010系统解算的UT1序列与国际GNSS监测评估系统(international GNSS monitoring and assessment system, iGMAS)解算的ΔLOD序列,运用Vondrak方法融合在一起,并通过MCMC算法估计最优的权重比。最后将该融合结果与IERS 14 C04 UT1序列进行比对,用以评估该融合方法的效能。
1 融合算法
1.1 理论支撑
UT1是由地球自转角定义的时间尺度,是与地球固连的地球坐标系(转动的地球坐标系,非惯性系)和天球坐标系(无旋转惯性系)间的重要的坐标变换参数。ΔLOD是描述地球自转运动的主要参量之一,代表了天文意义上的1 d与标准日长86 400 s之间的差别,体现了地球自转角速度的快慢。UT1和ΔLOD间存在的关系如下:
d(UT1-TAI)/d=ΔLOD
(1)
式中:TAI为国际原子时。
对于连续的ΔLOD序列,积分后就是UT1 相对某一初值的变化量,利用GNSS卫星数据估计ΔLOD已经成为例行的工作。国外,美国海军天文台、喷气推进实验室、布拉格天文研究所已进行了相关融合算法的研究。
1.2 Vondrak算法
本文采用Vondrak平滑组合算法对中国科学院国家授时中心(National Time Service Center, NTSC)VLBI2010系统解算的UT1数据与iGMAS解算的ΔLOD数据进行加权融合。该组合平滑算法是由Vondrak和 Cepek在2000年针对 UT1与ΔLOD融合问题而提出的。该算法不但能够对等间距和等精度的测量数据进行平滑处理,而且能够对不等间距和不等精度的数据进行处理,在天文学上使用广泛,比如国际地球自转服务、原子尺度平滑、恒星天文学分析。
关于一组测量数据(,) (=1,2,…,),其中是自变量,是对应自变量的测量值,Vondrak算法的理论思想如下:
=+=min
(2)
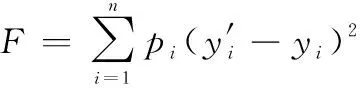
(3)
(4)

Vondrak算法使用多项式形式来表示平滑函数,多项式的一般形式如下:
(5)
对式(5)中求三次导并代入式(4)得到
(6)
当式(2)取得最小值时,有

(7)
将式(3)与式(6)代入式(7),便可获得Vondrak平滑方法的基础方程组:
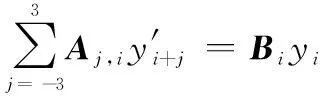
(8)
其中系数矩阵,和中的系数为
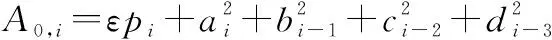
在原有的Vondrak方法上,增加一阶导数拟合度的定义,即Vondrak组合平滑算法:
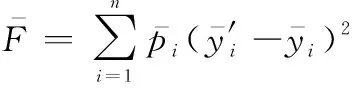
(9)
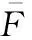
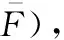
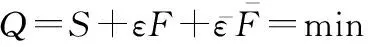
(10)
运用上述Vondrak求解的过程,即可求得具体的方程解。
1.3 MCMC方法及权重选取
由上述理论可得,观测值越接近于平滑值,则权重应该越大;产品的测量精度越高,则权重越大。实际使用中,权重直接影响最终融合产品的平滑效果和精度水平。由于实测UT1序列存在精度和时间间隔的不确定性,很难通过直接的理论推导方式得到最优的权比,因此本文通过MCMC的方法结合与事后精密EOP数据的比对,尝试得到对UT1观测值及一阶导数值ΔLOD的最优权重比。
MCMC方法是处理多维、复杂问题的常用方法,在空间物理学、图像分析、金融等领域发挥了重大的作用。该方法的基本思路是基于某种采样的方法进行大样本随机采样,来构造一个平稳分布的马尔可夫链,再对这些样本进行蒙特卡罗模拟,获得有效的统计量。
本文针对UT1及ΔLOD的权重优化问题,对UT1和ΔLOD的权重做大样本随机采样,采样方法为吉布斯采样,通过将二维空间采样变成一维空间,显著提高了MCMC方法的收敛速度。
2 输入数据源
2.1 UT1数据
采用的UT1数据是由NTSC的国内宽带VLBI2010系统自主测定的UT1序列。
为满足国家UT1测量需求,NTSC和上海天文台共同研制了我国首套宽带VLBI2010系统,由三亚观测站、吉林观测站、喀什观测站,及西安数据处理中心组成。自2018年以来,NTSC利用VLBI2010系统已开展了上百次常规的UT1观测试验。基本工作流程是吉林、三亚、喀什三站同时根据观测纲要开始观测,采集并记录观测数据,数据上传至西安数据处理中心;观测数据进行相关处理及后相关处理得到经过时延校准的射电源时延序列;进而结合三站气象站数据,最终通过数据分析软件对时延结果运用最小二乘算法进行解算,确定UT1。
本文使用了2018年和2020年由NTSC通过VLBI2010系统自主测量并解算的UT1序列。2018年选取了从2018年7月24号到2018年9月20号的时间段,共53次观测数据。2020年选取了从2020年8月14号到2020年11月4号的时间段,共68次观测数据。
2.2 ΔLOD数据
采用的ΔLOD数据有两种来源,分别是来自于iGMAS解算的ΔLOD产品,此产品用于实测验证。以及国际GNSS服务(International GNSS Service, IGS)提供的ΔLOD产品,此产品用于仿真验证。
2.3 事后精密EOP 数据
事后精密C04序列,从巴黎天文台服务器下载,其中eopc04_IAU2000.62-now和eopc04.62-now文件格式相同,主要的差异是天极轴改正项岁差-章动与IAU模型的偏差修正项,两个文件对应的岁差-章动模型分别为IAU2000A岁差-章动模型和IAU1980岁差-章动模型。由于C04序列是事后精密产品,故而时效性不高,主要用于精度比对和研究。
3 仿真分析
为了评估及优化融合算法,同时优化和指导NTSC 的VLBI2010系统UT1测定方案,根据文献[40]中提到的NTSC的VLBI2010系统实测UT1精度为58.8 μs,且不能连续观测的现状,仿真环节进行权重的仿真、时间间隔仿真、随机误差仿真及系统偏差的仿真,并研究输出序列与这些变量间的依赖关系。
3.1 时间间隔采样仿真
天文观测会受到恶劣天气、设备维护、仪器故障乃至网络中断等突发状况导致观测的不连续和中断。针对这种现象,需研究不同间隔的UT1数据对融合精度产生的影响。故而仿真了不同间隔的UT1实验,用于指导实际的UT1观测。
仿真分析的流程图如图1所示。
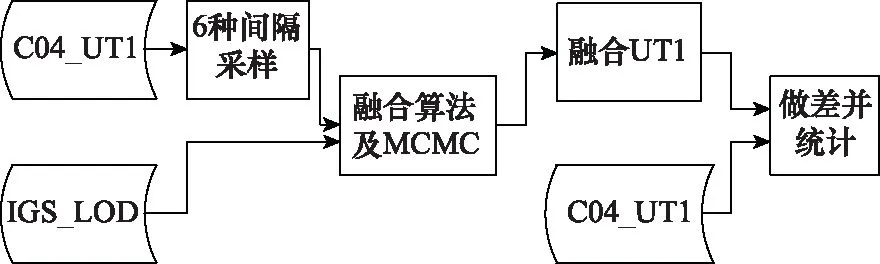
图1 时间间隔仿真Fig.1 Time interval simulation
利用不同时间间隔采样的精密C04序列替代NTSC解算的UT1序列,并与IGS的ΔLOD序列进行融合。分别进行间隔为1 d、2 d、3 d、4 d、5 d、6 d采样的仿真实验。对每种仿真实验通过MCMC算法,确定最优权重比和最优的融合结果,最后将融合的结果与C04序列做差,统计其标准差和权重比值(UT1/ΔLOD)。如表1所示,列代表对应的采样间隔,依次为1 d、2 d、3 d、4 d、5 d、6 d,行代表对应的权比和标准差,其中标准差单位为μs。

表1 不同采样间隔权重比值及标准差
可以得出采样的时间间隔越长,融合的精度就越低。同时,随着采样间隔的增加,UT1与ΔLOD的权重比呈现下降的趋势,表明权重与数据量有很强的相关性。这是因为采样间隔越长,UT1有效的数据量就越少,进而UT1对于融合的贡献也就越少,权重也会相应地降低,所以随着采样间隔的增加,融合精度出现下降的趋势。
3.2 随机误差仿真
研究随机误差对融合精度的影响,分别在精密C04序列的基础上加0 μs、10 μs、20 μs、30 μs、40 μs、50 μs、60 μs的高斯白噪声,再对加噪声之后的C04序列进行间隔为1 d、2 d、3 d、4 d、5 d、6 d的采样,共计42种UT1仿真序列,再与ΔLOD序列进行融合,将融合后的UT1与精密C04序列的进行做差,最终统计标准差,42种随机误差仿真实验的结果如表2所示,行代表对应的采样间隔,列代表对应的随机误差值,表中数值即为融合得到的UT1精度值。
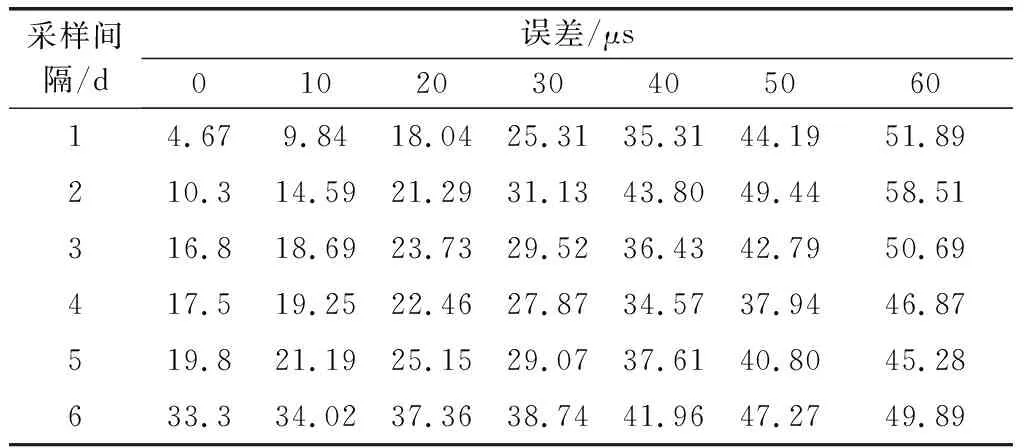
表2 误差仿真
使用折线图更直观地展示采样间隔与随机误差对融合UT1产品的影响,如图2所示,横坐标代表采样间隔,以d为单位,纵坐标为标准差,以μs为单位,图中折线从下往上依次为0 μs、10 μs、20 μs、30 μs、40 μs、50 μs、60 μs的随机误差。
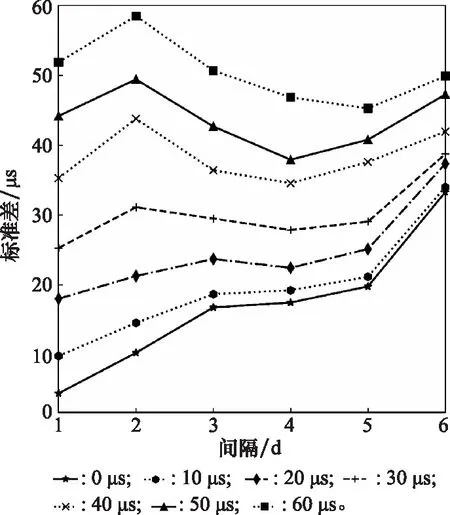
图2 误差仿真折线图Fig.2 Error simulation line chart
随机误差的仿真实验,可以得出,原始数据随机误差越大,融合精度就越低。随机误差与采样间隔共同影响着融合精度,对于采样间隔1 d和2 d的UT1数据来说,随机误差的影响占主导地位。随机误差对于精度有很强的相关性。当采样间隔大于2 d之后,采样间隔的作用逐渐明显,此时融合精度与随机误差不再是简单的正相关。当随机误差为50~60 μs时,采样间隔为3~5 d,融合效果较好。
3.3 系统偏差仿真
研究系统偏差对融合效果的影响,分别在精密C04序列的基础上加0 μs、10 μs、20 μs、30 μs、40 μs、50 μs、60 μs的系统偏差,生成7种UT1仿真序列,用该仿真序列分别替代NTSC解算的UT1序列,再与ΔLOD序列进行融合,将融合后的UT1序列与精密C04序列进行做差,统计标准差和均值,如表3所示。

表3 偏差仿真
可以得出系统偏差对于融合精度没有影响,改变系统偏差,融合结果的精度没有变化,这是因为系统偏差是一个固定值,只会影响整体的平移,不会影响稳定性,所以不会改变标准差,对于融合算法没有明显的作用。因此,UT1的系统偏差,如站坐标、大气模型不准导致的系统偏差,只能通过其他方法改正。
4 实测数据集融合
4.1 2018年实测数据集融合
使用NTSC于2018年下半年通过VLBI2010系统自主观测并解算的UT1实测数据集,选取简化儒略日58 323~58 381共59天的数据,采用3sigma原则对误差较大的数据进行剔除,将处理后的数据与iGMAS解算的ΔLOD数据集进行Vondrak平滑算法融合,并通过MCMC进行权重的最优化,在进行了1 000次的MCMC循环采样后,得到UT1与ΔLOD的权重比值收敛于0.176(UT1/ΔLOD),此时融合之后的UT1序列收敛于一个稳定值,将该稳定值与精密C04数据进行比对分析,工作流程图如图3 所示。
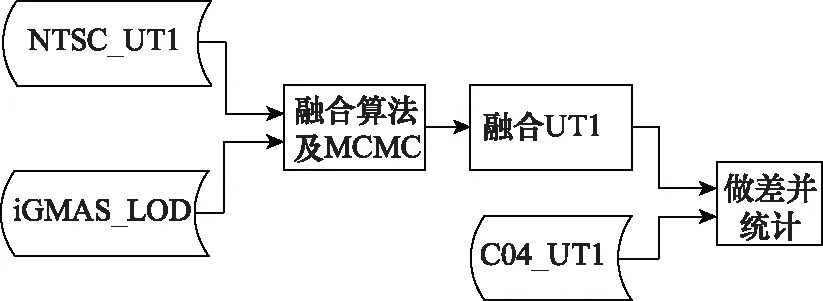
图3 工作原理流程图Fig.3 Working principle flow chart
图4(a)展示了3种UT1数据,分别为精密C04序列的UT1数据、NTSC解算的初始UT1数据和使用融合算法得到的融合UT1数据。其中横坐标为简化儒略日,纵坐标单位为s,黑色、蓝色、红色的标识分别代表精密C04的UT1、NTSC初始UT1、融合UT1。图4(b)纵坐标单位为μs,红色、蓝色标识分别代表融合UT1与C04_UT1的差值、NTSC初始UT1与C04_UT1的差值。
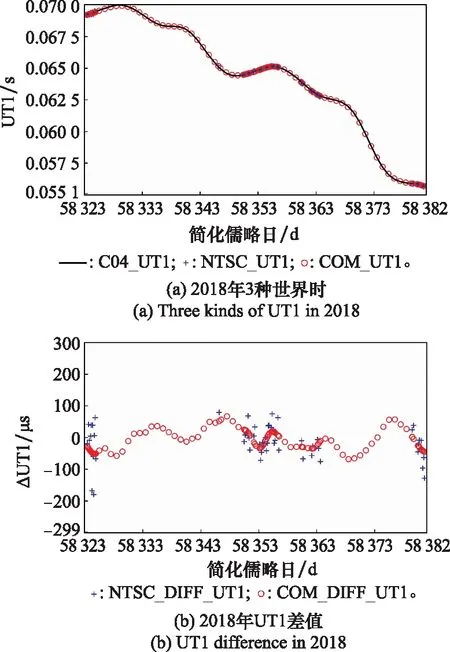
图4 2018年UT1数据比对分析Fig.4 Comparison and analysis of UT1 data in 2018
使用直方图对图4(b)差值进行统计分析,如图5所示,横坐标为差值,单位为μs,纵坐标为归一化后的值,代表数量,因融合后的UT1更加密集,故而进行归一化处理。蓝色、红色分别为NTSC初始UT1与精密C04_UT1的差值,融合UT1与精密C04_UT1的差值。图6纵坐标代表差值,单位为μs。
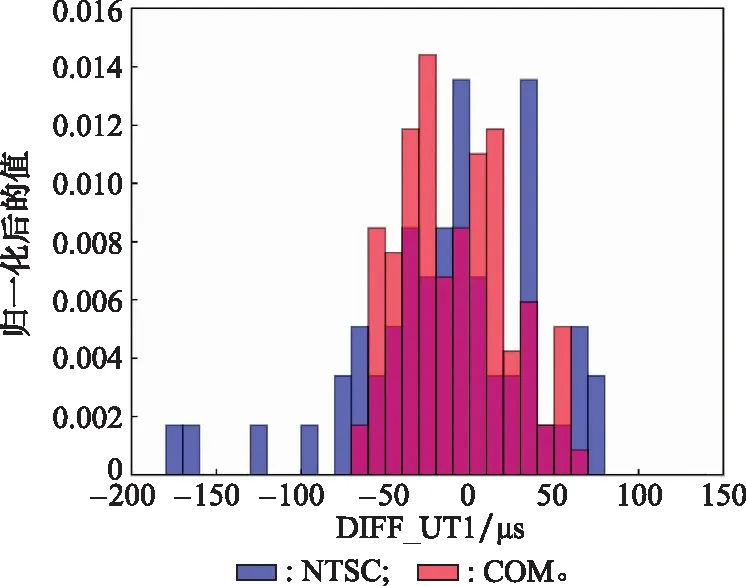
图5 2018年融合前后UT1精度比对Fig.5 Comparison of UT1 accuracy before and after combination in 2018
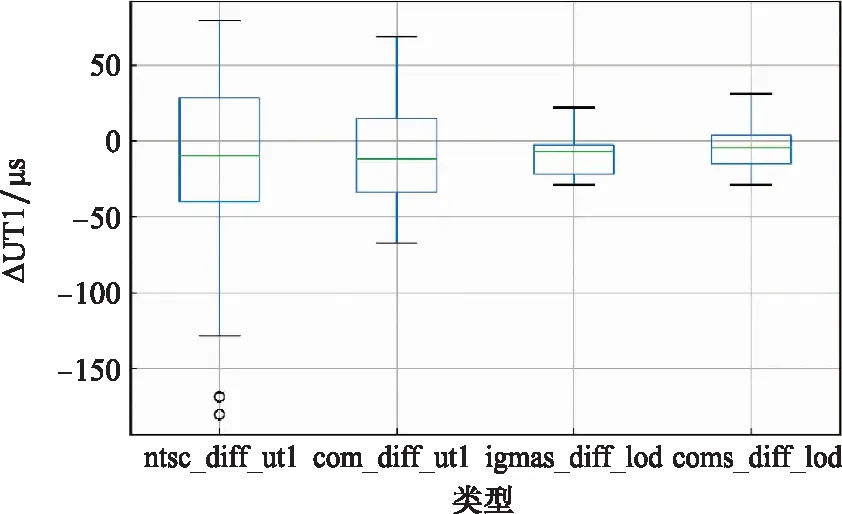
图6 2018年融合前后产品比对Fig.6 Comparison of products before and after combination in 2018
为了更具体地展示融合精度,统计了差值的均值、标准差、中位数、最大值及最小值,如表4所示。

表4 2018年精度统计分析
图5显示,融合后的数据集相对IERS事后精密序列的偏差集中在-50~50 μs之间,相比之下,初始UT1数据的偏差分布集中在-80~80 μs之间。图6直观地展示了融合后的数据要比原始数据更为稳定。通过表4得出NTSC初始UT1标准差为53.18 μs,融合UT1标准差为31.96 μs,融合后的均值、最值均比原始序列更小,经过融合算法,得到更连续、更稳定的UT1序列,其精度提高了37%。
4.2 2020年实测数据集融合
根据2020年NTSC开展的UT1观测实验,选取了简化儒略日59 075~59 157共83 d较为连续的观测数据。将处理后的2020年NTSC解算的UT1数据与iGMAS解算的ΔLOD数据集进行Vondrak平滑算法融合,并通过MCMC进行权重的最优化,在进行了1 000次的MCMC循环采样,得到UT1与ΔLOD的权重比值收敛于2.774 6,此时融合之后的UT1序列收敛于一个稳定值,将该稳定值与精密C04数据进行比对分析(方法与2018年相同),结果如图7所示。
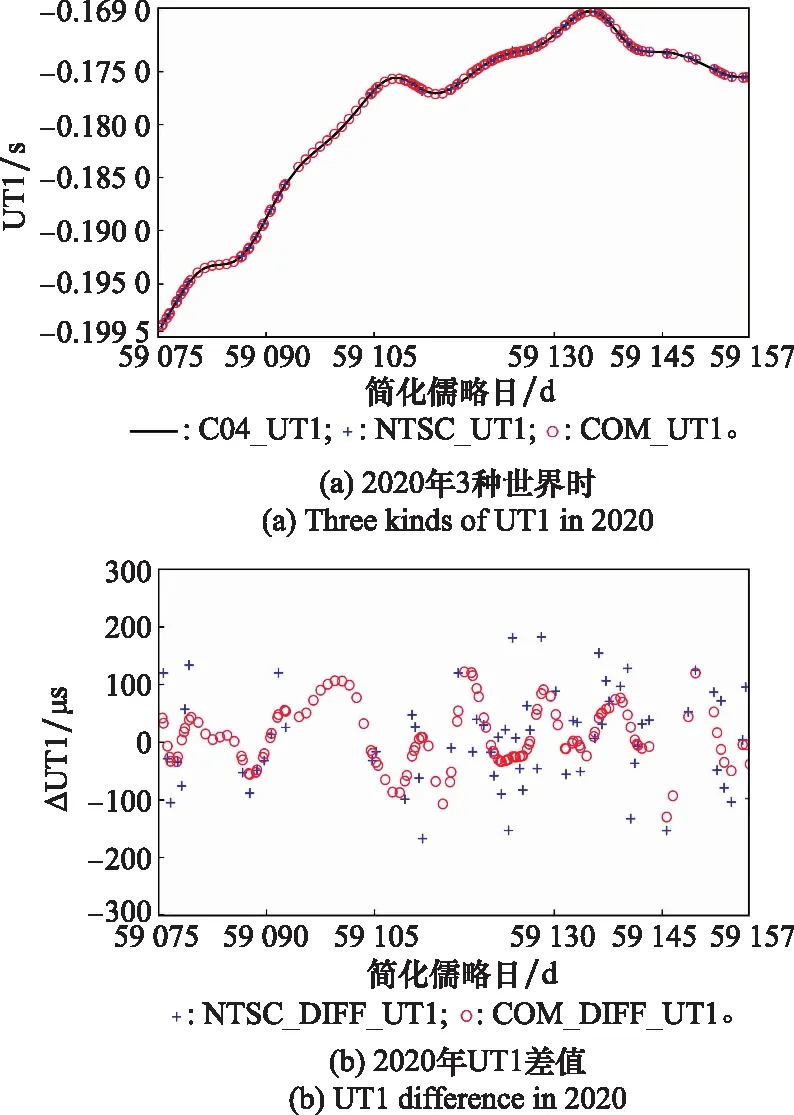
图7 2020年UT1数据比对分析Fig.7 Comparison and analysis of UT1 data in 2020
均值、标准差、中位数、最大值及最小值统计结果如表5所示。
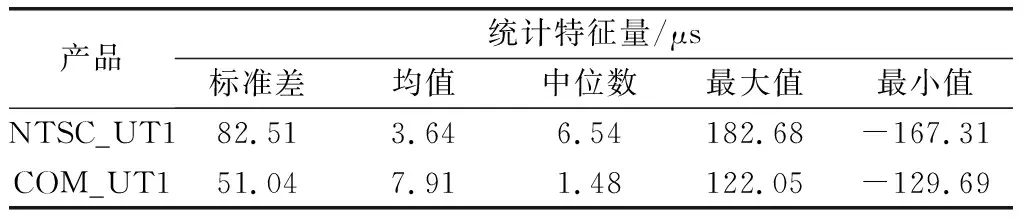
表5 2020年精度统计分析
图8显示,融合后的数据集相对IERS事后精密序列的偏差集中在-60~60 μs,相比之下,初始UT1数据的偏差集中在-100~100 μs。图9直观地展示了融合后的数据要比原始数据更为稳定。通过表5得出NTSC初始UT1标准差为82.51 μs,融合UT1标准差为51.04 μs,融合后的中值、最值均比原始序列更小,经过融合算法,得到更连续、更稳定的UT1序列,其精度提高了38%。

图8 2020年融合前后UT1精度比对Fig.8 Comparison of UT1 accuracy before and after combination in 2020
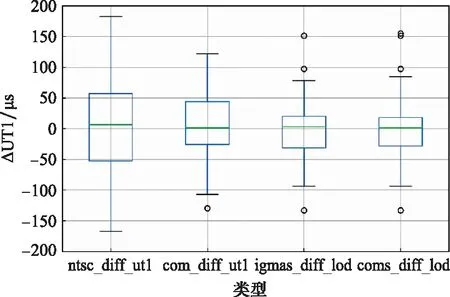
图9 2020年融合前后产品比对Fig.9 Comparison of products before and after combination in 2020
需要指出的是,通过比对与MCMC结合的方法,得到的最优权重比,是一种事后评估行为,实际使用过程中,该最优权比的有效性建立在短期内测量精度及频度基本稳定的前提下。若实测精度与频度发生改变,则权比也应酌情调整。在绝大多数实际应用中所采用的权比,并非理论的最优值,而是通过比对和分析,努力从观测和算法两方面共同去维持和逼近理论上最优的权比,以得到更稳定的UT1序列。
5 结 论
针对国内UT1序列精度提升问题,本文研究了一种基于国内数据的UT1/ΔLOD融合方法,该方法通过Vondrak方法及MCMC算法进行最优权重的融合。并结合UT1采样时间间隔、随机误差、系统偏差的仿真实验来进一步指导NTSC的VLBI2010系统UT1观测,主要结论如下。
(1) 对于NTSC的 VLBI2010 系统,由于其精度为58.8 μs,通过随机误差仿真实验得出,实测VLBI观测的采样间隔为3~5 d时(平均每周2次观测),融合后的UT1产品精度最高。
(2) 合理观测频度、持续的比对及融合权比的优化,可有效提升最终UT1产品序列的精度、稳定度及连续性。该融合方法对2018年和2020年自主测量的UT1序列精度的提升效果均超过30%。

