基于偏微分方程与维纳滤波模型的图像去噪
刘光宇,曾志勇,曹 禹,赵恩铭,邢传玺
(1.大理大学 工程学院,云南 大理 671003;2.哈尔滨工程大学 物理与光电工程学院,黑龙江 哈尔滨 150001;3.云南民族大学 电气信息工程学院,云南 昆明 650031)
由于受设备、环境以及人为因素的干扰,图像中通常包含了运动模糊和高斯白噪声,影响机器以及人们对图像信息的获取.因此,图像去噪是图像信息获取过程中不可缺少的一部分[1],传统的图像去噪方法会模糊图像的边缘和细节.为了减少去噪过程中产生的不利影响,学者们开始着手研究各种高阶去噪模型[2-4].张晓娟研究的偏微分方程图像去噪模型有良好的数学理论基础,且具有较强的局部自适应性和高度的灵活性[5].之后,呼亚萍、孔韦韦等人提出了一种TV全变分图像去噪模型,该方法能够理想去除图像中的噪声,使处理后图像的PSNR、熵和MSE 评价指标数值有较好的表现,但其算法的平均运行时间较长[6].2020年,黄培研究指出,维纳滤波的优点是能够规避处理频域时会出现的病态问题,当PSF 已知时,对模糊图像的复原效果更加显著,但它所采用的最小均方误差准则和人的视觉并不是完美契合的[7].黄金、周先春、吴婷等提出了一种混合维纳滤波与改进型TV 的图像去噪模型,该模型能够有效去除噪声、强化边缘,有效地保证了边缘结构的细节信息[8].
因此,为了解决去噪过程中造成边缘细节和纹理特征模糊的问题,本文利用TV 全变分偏微分方程模型与维纳滤波模型相结合的方法对图像进行去噪处理,并通过仿真实验验证了该方法的可行性.
1 TV 模型与维纳滤波模型
1.1 TV 模型
TV 模型是基于偏微分方程去噪模型中的经典,它对于很多图像噪声污染问题有着明显的作用,且因该模型能有效保留图像的边缘部分并消除图像中的噪声,到目前依然受到相关邻域研究者的青睐[9].

TV 模型定义的能量函数为[10]:
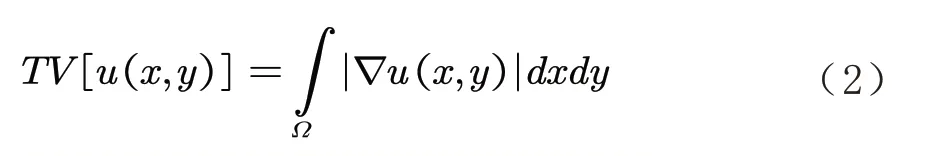
并且满足噪声约束:
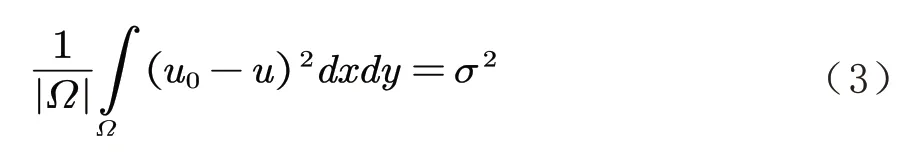
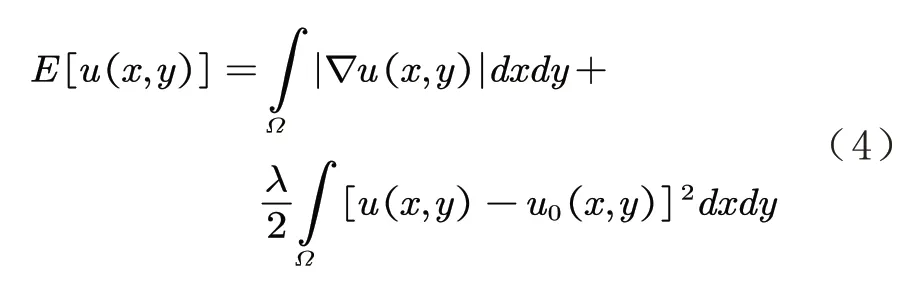
在实际的图像处理中,被污染的图像可以看作是几乎处处连续的原函数,通过上述算法可对原函数图像进行运算,即将被污染区域与相邻的区域进行积分,通过调整相关参数来改变算法的运算条件,从而达到去噪的目的.TV 模型通常通过改变运算的迭代次数,来达到理想的去噪效果.不同的迭代次数,具有不同的去噪效果.当迭代次数过低时,图像中的噪声无法得到有效去除,当迭代次数过高时,图像的边缘细节会出现模糊的情况,影响整体图像质量.因此,使用TV模型进行去噪时,需要选择合适的迭代次数.
1.2 维纳滤波模型
维纳滤波器是一种线性滤波器,通常被用于在被污染信息中提取有用的信号[12].维纳滤波器基于最小均方误差准则[13],其去噪原理图如图1 所示.

图1 维纳滤波器去噪原理

均方误差则为:

维纳滤波的目的在于推导均方误差为最小值时的滤波器系数,即:
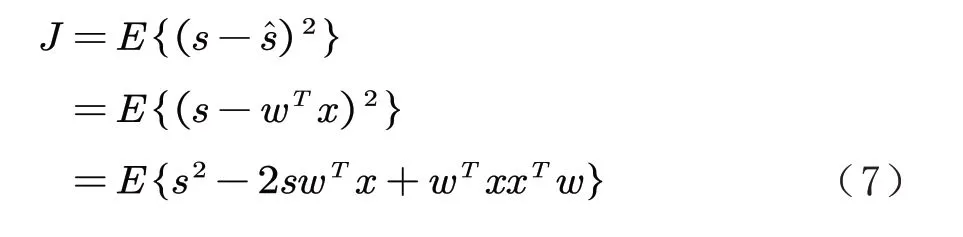
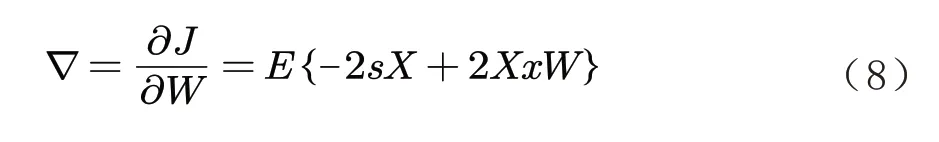
令上式值为0,即可求出极值点:
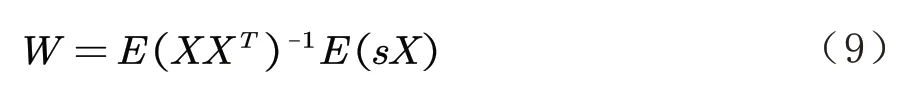
由于实际情况下无法准确得到理想的统计参数,因此通常采用实际输入信号的相关采样来进行估计.该公式也被称为维纳-霍夫方程[14],是最小均方误差准则下的滤波器系数最优解法.
维纳滤波器在实际中应用领域广泛,包括噪声抑制,系统识别,预测等,本文主要利用其噪声抑制特性对图像进行处理.
1.3 TV 模型与维纳滤波模型的结合
当在无噪声干扰的情况下,维纳滤波器的功能相当于逆滤波,设原始图像为降质函数为则最终得到的降质图像为:

理想情况下的逆滤波为:

式(11)可以看作是降质函数的逆反过程,理论上可以完全恢复图像,但在实际情况下会存在噪声,因此设噪声为,则降质后的图像为:
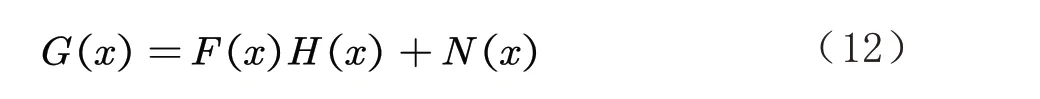
此时对降质图像的逆滤波过程变为:
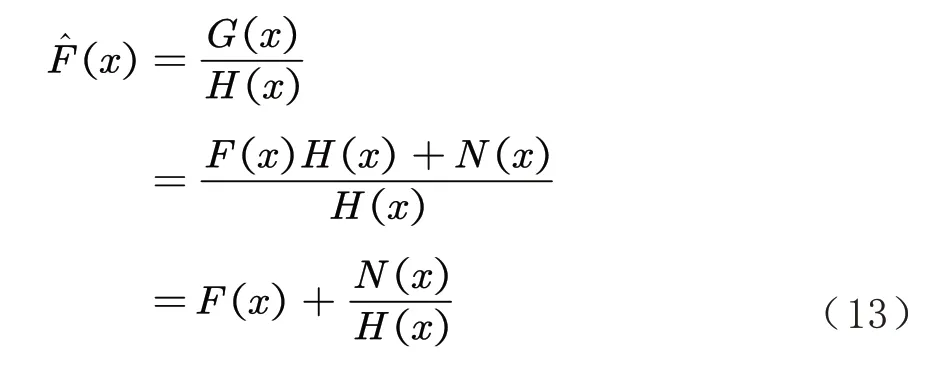
实际处理情况下,TV 模型不可能完全去除图像中的噪声,因此在实际处理情况中,若给定一个系统:
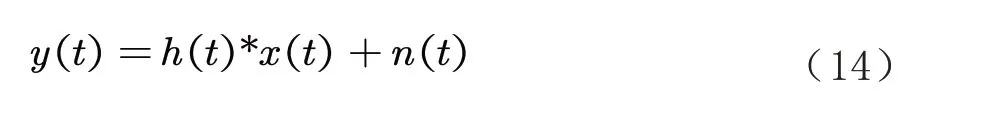

基于这样的误差度量,滤波在频域的描述为:
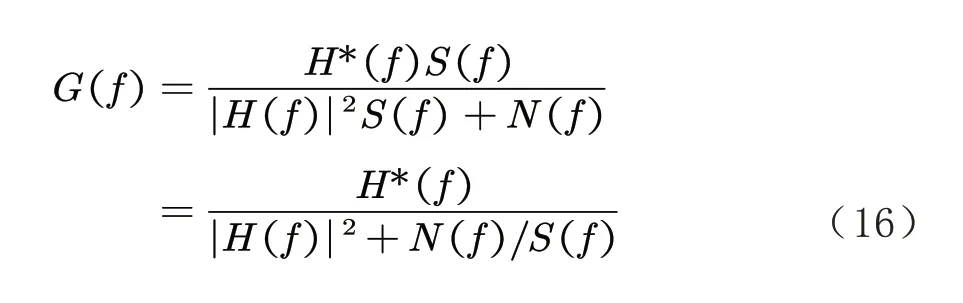
由式(16)可以看出,当噪声为零,信噪比的值趋近无穷,此时的维纳滤波可以简化为逆滤波,但当噪声增加时,会影响到维纳滤波的整体效果,即维纳滤波的最终结果依赖于信噪比的取值.
因此,处理带噪声图像的处理过程中可以结合使用TV 模型,TV 模型能在保留图像原有信息的基础上有效提高信噪比,并且通过调整迭代次数可以得到更优的结果.
2 仿真实验
首先,选取大小为512×512 的轮船图像(图2a)作为实验对象,对其添加均值为0,方差为0.1的高斯白噪声和角度为0,位移为10 的运动模糊.然后利用中值滤波、均值滤波以及TV 模型与维纳滤波模型相结合的方法对含噪图像进行去噪处理,其中TV 模型的迭代次数设为10,处理结果如图2 所示.


图2 轮船图像
从图2(c)(d)(e)可以看出,通过中值滤波处理后,图像的对比度得到了提升,但其去噪效果并不明显.通过均值滤波处理后,图像的去噪效果相比中值滤波有一定程度的提高,但其对比度降低,直观视觉效果较差.采用TV 模型与维纳滤波模型相结合的方法对图像进行处理后,图像中的噪声得到很大程度的滤除,同时边缘细节保存较为完整,视觉效果改善明显.从直观视觉的角度证明了该方法的可行性和有效性.
为进一步客观具体地评估所采用的方法,通过计算图像的均方误差(Mean Squared Error,MSE)、信噪比(Signal to Noise Ratio ,SNR)、峰值信噪比(Peak Signal to Noise Ratio,PSNR)以及结构相识度(Structural Similarity,SSIM)来对图像质量进行判断.MSE、SNR、PSNR 和SSIM的计算公式如下:
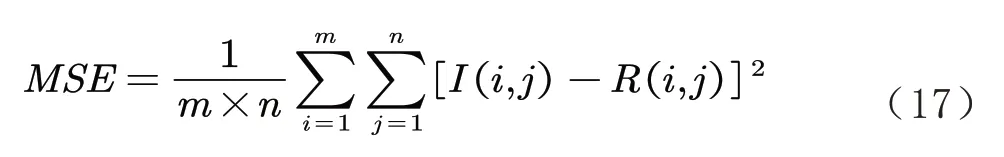
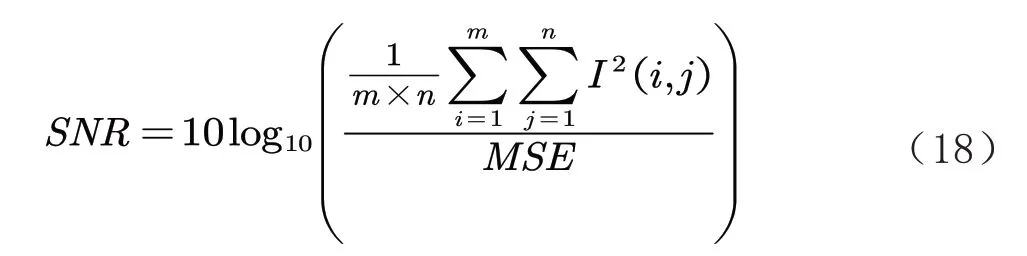
式中的参数表示与式(17)相同.
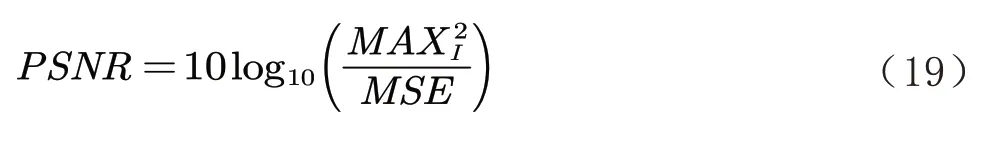
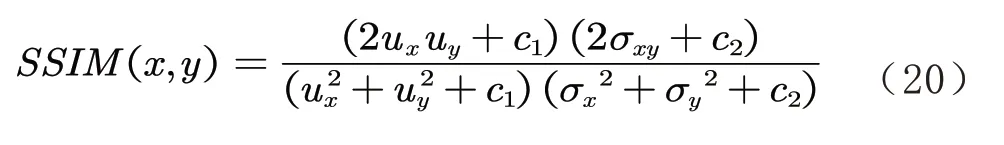
图2(b)(c)(d)(e)中的各项质量评价指标如表1 所示.
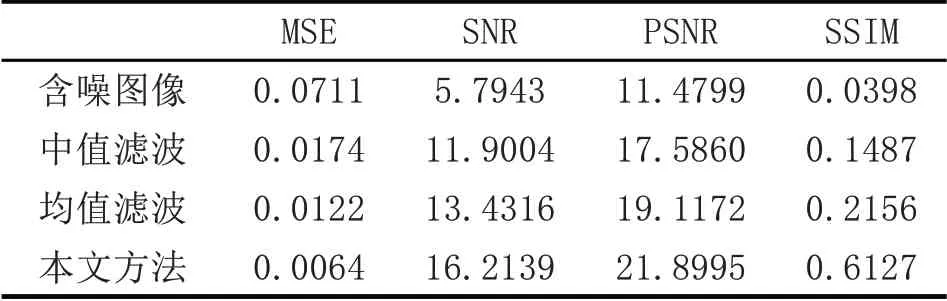
表1 轮船图像质量评价指标(dB)
从表1 中的实验数据可以看出,通过中值滤波和均值滤波方法去噪处理后,图像中的SNR 值、PSNR 值和SSIM 值都有一定程度的提升,MSE 值有一定程度的下降.通过TV 模型与维纳滤波模型相结合的方法进行处理后,图像的SNR 值从5.7943 提升至16.2139;PSNR 值从11.4799 提升至21.8995;SSIM 值从0.0398 提升至0.6127;MSE 值从0.0711 下降至0.0064,各项数据都明显优于中值滤波法和均值滤波法.
由于TV 模型的迭代次数对实验结果有一定影响,故对迭代次数进行进一步研究.选取大小为512×512 的石柱图像,对其添加均值为0,方差为0.1 的高斯白噪声和角度为0,位移为10 的运动模糊.利用TV 模型与维纳滤波模型相结合的方法对含噪图像进行处理,其中TV 模型的迭代次数分别选取为5 次、10 次、15 次、20 次、25 次和30次,得到的结果与中值滤波、均值滤波进行对比.实验结果如图3 所示.

图3 石柱图像
从图3 可以看出,随着迭代次数的增加,TV 模型与维纳滤波模型相结合的方法的去噪能力逐渐增强,图像中的噪声得到进一步滤除.但同时也要避免迭代次数过大,以防止细节信息丢失.通过计算图3 各子图像的MSE 值、SNR 值、PSNR 值和SSIM 值,对去噪效果进行比较.计算结果如表2 所示.
从表2 中可以看出,当迭代次数为5 至30 次时,TV 模型与维纳滤波模型相结合的方法的SNR值、PSNR 值和SSIM 值都明显高于中值滤波法和均值滤波法;MSE 值明显低于中值滤波法和均值滤波法,表明在合适的迭代次数范围内,TV 模型与维纳滤波模型相结合的方法在上述三种方法中去噪效果最好,失真程度最小,边缘保持能力最强.
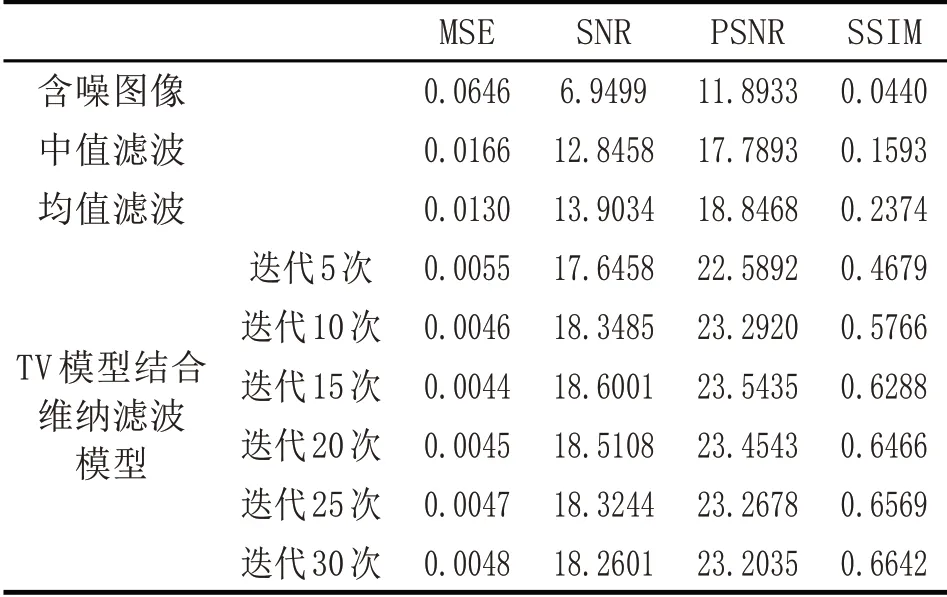
表2 石柱图像质量评价指标
3 结语
本文介绍了TV 全变分偏微分方程模型和维纳滤波模型的基本概念,并结合两种模型的去噪优势对含噪图像进行处理.仿真结果表明,无论从直观图像还是客观数据,本文所采用的方法都更为有效地提升了图像的整体质量,使去噪后的图像进一步接近原始图,验证了该方法的可行性和有效性.

