考虑交直流多谐波耦合的模块化多电平换流器矩阵建模

张海川，王顺亮，刘天琪，董语晴，陈相

(四川大学 电气工程学院， 成都 610065)

0 引 言

模块化多电平换流器(Modular Multilevel Converter，MMC)相较于传统的电网换相型换流器具有有功、无功独立控制和可靠性高、便于维护[1-2]等优势，在异步电网互联和新能源接入等方面有着广泛的应用[3]。然而，交直流系统的背景谐波经过MMC换流器的调制作用可能发生互相耦合，形成AC/DC之间的正反馈闭环，造成谐波来回振荡放大，最终可能引发谐波不稳定[4-6]。谐波耦合矩阵模型是一种分析复杂电力电子系统谐波传导与耦合机理的有效工具，但同时MMC换流器运行方式复杂、各电气量相互影响的特点给其谐波耦合建模带来一定的难度[7-8]。

文献[9]提出了基于开关函数的MMC谐波传导模型，其一次可对某特定次数谐波的传导特性进行讨论；文献[10-11]中提出了考虑内部动态特性以描述MMC交、直流侧电气量耦合关系的状态空间矩阵模型，但其只限于讨论直流线路直流电气量与交流系统基频电气量的幅值耦合关系，而不能描述各电气量谐波的耦合特性；文献[12]提出了谐波状态空间(Harmonic State Space， HSS)基础理论，该理论采用复数傅里叶分解与傅里叶级数相乘定理以使周期时变模型定常化；文献[13]提出了基于谐波状态空间的MMC交流侧阻抗建模方法，其通过研究换流器交流谐波电压与谐波电流间关系以得到换流器交流侧等效阻抗，但没有对直流电压与直流电流、直流电气量和交流电气量间谐波耦合关系进行建模分析。为了同时考虑MMC交直流侧各量所有次数谐波间耦合关系，将谐波状态空间与开关函数结合以建立MMC换流器的谐波耦合矩阵。MMC谐波耦合矩阵模型采用开关函数以分别描述特定次数谐波间耦合关系；再采用谐波状态空间理论将系数矩阵中的周期时变量(由开关函数产生)展开为常复数以克服模型系数矩阵中含有时变量的问题，且展开后的模型可同时描述所有次数谐波间耦合关系。

在加入谐波扰动后，将搭建的MMC谐波耦合矩阵模型的计算结果与PSCAD电磁仿真模型进行对比，验证了MMC谐波耦合矩阵模型对MMC换流器交直流侧电压电流的各次谐波间耦合关系描述的准确性。

1 MMC换流器时域模型

1.1 MMC换流器桥臂平均模型

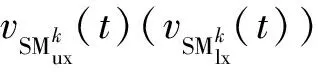
图1 MMC换流器详细模型Fig.1 Detailed model of MMC converter

(1)

(2)

(3)

(4)

式中Carm=CSM/N为桥臂等效电容。

1.2 MMC换流器时域状态空间小信号模型

根据桥臂平均模型，MMC换流器及其交流系统可等效为如图2所示结构，其中igx(t)为换流器x相输入电流，则MMC换流器与交流系统具有如式(5)所示电流关系。

图2 MMC换流器桥臂平均模型Fig.2 Average model of bridge arm of MMC converter

(5)

式中icx(t)为换流器x相环流，其值为该相上桥臂、下桥臂电流的平均值。

将式(3)～ 式(5)进行小信号化，可得MMC桥臂平均小信号模型，其中MMC换流器考虑为开环控制，即开关函数nux(t)、nlx(t)的变化量Δnux(t)、 Δnlx(t)均为零，结果如式(6)～式(8)所示。

(6)

(7)

(8)

将式(6)～式(8)转化为状态方程形式，得到MMC换流器的单相时域状态空间小信号模型，如式(9)所示。

(9)

其中：

上述讨论中，nux0(t)、nlx0(t)分别为x相上桥臂、下桥臂开关函数的稳态值，其由MMC的控制系统决定，其组成如式(10)所示。

(10)

其中：

vref1x(t)/vdc0=m1cos(ω0t+θm1x)

vref2x(t)/vdc0=m2cos(2ω0t+θm2x)

式中ω0为系统的基频角频率；vdc0为直流电压稳态值，其值为常数；vref1x(t)为由MCC基本控制器产生的x相参考电压波基频分量，其相位为θm1x；vref2x(t)为由环流抑制控制器产生的x相参考电压波二次谐波分量，其相位为θm2x；m1与m2分别为基本控制器与环流抑制控制器的调制度。

2 MMC换流器频域模型

2.1 谐波状态空间理论

MMC换流器作为典型的时变系统，其状态变量和输入、输出变量间具有如下关系：

(11)

当系统正常运行到稳态时，其内部各个状态变量的时域响应都具有周期性的特点，故将式(11)中状态变量x(t)复数傅里叶分解展开，并将其乘以est以描述信号的暂态过程，则式(11)中状态变量及其导数写为：

(12)

(13)

式中n为谐波次数；xn表示x(t)的第n次谐波的复傅里叶系数；ω0为系统的基频角频率。同理，输入变量u(t)与输出变量y(t)可写为：

(14)

对于系数矩阵A(t)，其组成均为稳态量而不存在任何暂态过程，可直接写成傅里叶级数形式如式(15)所示，其中An为A(t)的复数傅里叶分解的n次项系数，B(t)、C(t)、D(t)的傅里叶级数形式同理可得：

(15)

根据傅里叶级数的相乘定理，周期函数a(t)、b(t)与他们的时域乘积c(t)之间具有如式(16)所示关系[15]：

(16)

其中ck为c(t)的复数傅里叶分解的k次项系数，al与bk-l同理。则式(12)～式(15)中各变量和系数矩阵的傅里叶系数间具有如下所示关系：

(17)

式(17)即为谐波状态空间中第n次谐波的状态方程与输出方程。将各次谐波的状态方程联立，可将式(11)中的状态方程转化到谐波状态空间，其矩阵方程为：

sX=(A-N)X+BU

(18)

其中：

X=[x-h,…,x-2,x-1,x0,x1,x2,…,xh]T

U=[u-h,…,u-2,u-1,u0,u1,u2…,uh]T

N=diag[-jhω0I…-jω0I, zeros(m),jω0I, …

jhω0I]

式中h为考虑的最大谐波次数；zeros(m)为m阶零矩阵，I为m阶单位矩阵，m为时域系数矩阵A(t)的行列数；A、B为托普利兹(Toeplitz)矩阵形式；下标表示谐波次数。

同理可将式(11)中的输出方程转化到谐波状态空间，其矩阵方程为：

Y=CX+DU

(19)

式(18)与式(19)联立，即为周期时变系统的谐波状态空间模型，其系数矩阵与各变量均采用复傅里叶系数(常数)进行表示，实现了周期时变模型的定常化并可描述原时域变量的各次谐波分量间数学关系。

2.2 MMC换流器HSS小信号模型

如式(9)所示的基于开关函数建立的MMC换流器时域状态空间小信号模型的系数矩阵中包含周期时变量nux0(t)、nlx0(t)，使得模型不能求解而不具有实际意义。考虑谐波状态空间理论可将周期时变方程定常化的特点，将其带入式(9)中的时域状态空间模型，使之转化为频域的谐波状态空间模型并写为三相形式，如式(20)所示。

ΔXM=AMΔXM+BMΔUM

(20)

其中：

ΔUM=[ΔVga,ΔVgb,ΔVgc,ΔVdc]T；

P=diag(p,p,p,p)；

p=diag[jhω0, …,-jω0, 0, jω0, …, jhω0]。

式中h为考虑的最大谐波次数；I1为2h+1阶单位矩阵；ZM1为2h+1阶零矩阵；ZM2和ZM3为零矩阵，其分别与AMx和BMx行列数相同。所有变量以频域表示并以大写字母标识，其实质为由原时域周期时变量的复数傅里叶系数以(-h，…，-1，0，1，…，h)的谐波次序排列而成的列矩阵。ΔIgx的结构如式(21)所示,其他输入变量与状态变量同理可得。

(21)

式中 ΔIgx(h)为时域状态变量Δigx(t)的复数傅里叶分解的h次项系数。Γ代表Toeplitz矩阵，其结构如式(18)所示,则根据式(10)可得Γ[Nux0]的具体组成如式(22)所示，Γ[Nlx0]同理可得：

(22)

3 MMC换流器谐波耦合矩阵模型

MMC的HSS小信号模型如式(20)所示，其输入变量为换流器交流侧电压Δvgx(t)的各次谐波分量和直流侧电压Δvdc(t)的各次谐波分量。故为完整描述MMC两侧电气量各次谐波的耦合关系，取式(21)的输出变量为换流器交流侧各相输入电流Δigx(t)的各次谐波分量和直流侧输入电流Δidc(t)的各次谐波分量。Δigx(t)本身为状态变量，Δidc(t)可由式(23)计算：

(23)

则MMC的HSS小信号模型的输出方程如式(24)所示。

ΔYM=CMΔXM

(24)

其中：

ΔYM=[ΔIga,ΔIgb,ΔIgc,ΔIdc]T;

Cg=[ZM1,ZM1,ZM1,I1];

式中ZM4为与Cg为行列数相同的零矩阵。当系统加入小扰动后重新达到稳态时状态变量的导数为零，则此时MMC的HSS小信号模型的输入、输出变量有如式(25)所示对应关系：

(25)

式(25)即为MMC谐波耦合矩阵模型，其中Q为谐波耦合矩阵。式(25)也可写为如式(26)形式表示：

(26)

式中qmm为谐波耦合矩阵Q的m行m列(m=8h+4)位置元素。MMC谐波耦合矩阵模型的建模步骤如图3所示。

图3 建模流程图Fig.3 Modeling flow chart

MMC谐波耦合矩阵模型结合开关函数与谐波状态空间以描述MMC电气量的-h～h次数范围内谐波间耦合关系，当h足够大，理论可获得全部整数次谐波间耦合关系。

4 仿真验证

加入扰动后，将MMC换流器谐波耦合矩阵模型的计算结果与PSCAD电磁暂态仿真对比，以验证提出模型的准确性。

仿真工况： 1 s时交流系统公共点处加入31 kV三相正序二次谐波电压，并同时在直流接口加入27 kV二次谐波电压。通过MMC换流器谐波耦合模型计算得到a相交流电流iga(t)的0～3次分量的幅值Iga(0)、Iga(1)、Iga(2)、Iga(3)以及直流电流idc(t)的0～3次分量幅值Idc(0)、Idc(1)、Idc(2)、Idc(3)，与电磁暂态仿真值的对比结果如图4与图5所示。

图4 交流侧电流0～3次分量幅值Fig.4 Amplitude of 0～3 times component of AC side current

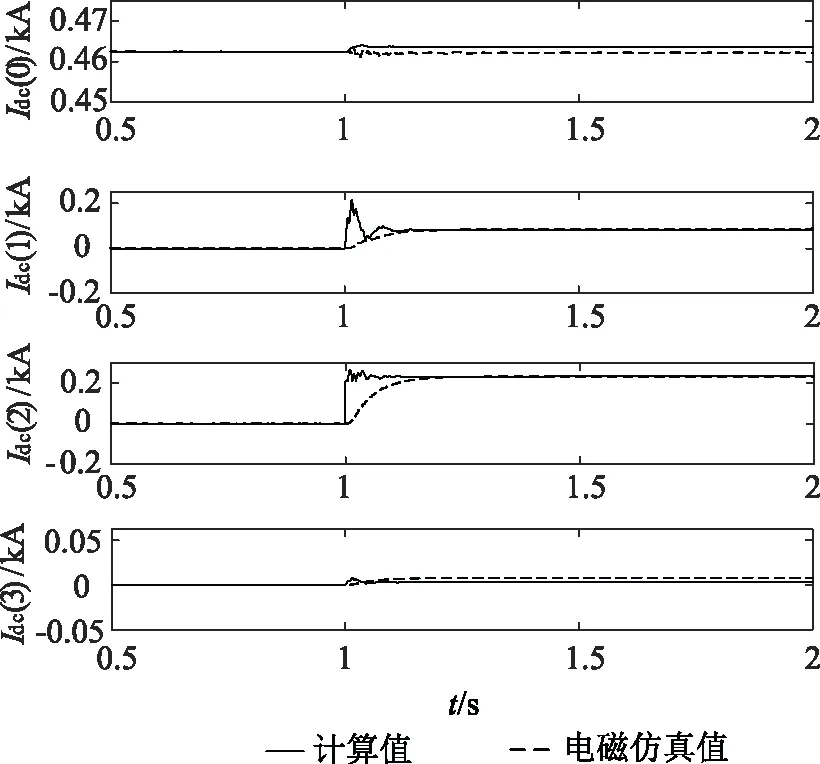
图5 直流侧电流0～3次分量幅值Fig.5 Amplitude of 0～3 times component of DC side current

MMC换流器谐波耦合矩阵模型通过矩阵计算直接得到加入扰动后换流器两侧电气量的各次谐波稳态值，故暂态过程与电磁仿真图像不重合，但收敛得到的稳态值与电磁仿真结果一致。

经过对比，加入谐波扰动后，MMC谐波耦合矩阵模型计算结果的谐波次数与幅值大小均与电磁仿真结果相符，验证了该模型对MMC换流器交直流侧谐波耦合特性描述的准确性。

5 结束语

能准确反应MMC谐波耦合特性的数学模型对包含MMC换流器的交直流互联系统谐波稳定性的研究至关重要。MMC换流器谐波耦合矩阵模型可同时描述MMC交、直流侧电气量所有次谐波间耦合关系。以上述耦合矩阵模型为基础，通过其特征值、参与因子、灵敏度等指标对MMC交直流互联系统谐波稳定性的进一步研究留待后续讨论。