基于隶属云和动态时间规整的电能计量误差估计方法

许灵洁，沈建良，郭鹏，陈骁，李志立

(1.国网浙江省电力有限公司，杭州 310000； 2.福建亿榕信息技术有限公司，福州 350003 )

0 引 言

在智能电网中，先进的计量基础设施(Advanced Metering Infrastructure，AMI)对于智能仪表数据的测量、双向通信、收集、分析和应用至关重要。通过AMI的应用，电力公司可以获取电能损耗和需求信息以改善电力调度和价格策略，并获得电力设备的状态信息以确保有效的管理和维护计划。电能计量装置作为AMI的核心部件，记录电能的区间消耗量，并将该信息及其自身的计量精度、时钟状态等状态信息反馈给电力公司。电能计量规范精度要求范围内的计量误差是诊断电能计量设备状态最常见、最直接的手段。计量误差来自四个地方，即电能表、电流互感器(Current Transformer，CT)、电压互感器(Voltage Transformer，VT)和二次电路[1]。由于误差源的多样性和不同误差源之间的内在关联性，现有的现场校准和周期性测试方法不能识别电能表的所有潜在危害[2]。然而，这些不正确的测量方法和仪表故障给电力公司带来了巨大的经济损失。在线监测是一种有效的方法，可通过检测不正确的测量读数并进行校正来发现电能计量设备的缺陷和故障(计量设备的接线错误，时钟异常等)。利用智能电能表数据和先进的数据挖掘方法，可以及早发现和预防电能计量设备计量误差的超限问题[3]。

电能表、电压互感器和电流互感器的计量误差随输入条件和外部环境的影响而动态变化[4-6]。文献[4]对校准装置重新设计,用校准电极对乘法器谐振进行校准,利用经过校准的乘法器测试电压显示值与等效电阻共同计算校准系数,利用校准系数建立数学模型对谐振影响产生的不确定度进行优化,完成了非接触式静电电压表校准方法的设计。对正弦和非正弦条件下、输入电压和电流不同时模拟电子瓦特计的功率和电能误差进行了测试。电能表和二次回路的误差可通过远程校准进行连续监测，VT和CT的误差不能直接测量[5]。计量误差可通过外推法估算，但该方法仅考虑了VT和CT的二次负载、一次电流和电压。影响VT和CT误差的主要因素有环境温度、外加电场和磁场、漏电流等[6]，这些因素对误差偏差的影响具有随机性和模糊性。

电能计量误差的影响因素众多，计量误差时间序列的幅值和形状的变化往往伴随着一些相似的单一或多个影响因素的变化。因此，通过误差时间序列与相关影响因素的相似性量化，可以证明计量误差与多因素之间的关系。多元时间序列的相似性可以用动态时间规整(Dynamic Time Warping，DTW)的距离方法来度量。DTW距离通过确定动态规整路径的最小代价来拉伸和压缩时间轴，以确保不同时间序列之间的最佳匹配[7]。同时，文献[8]提出了针对风电机组状态模糊综合评估存在评估指标权重和隶属度确定主观性强的问题,提出了一种基于最优权重和隶属云的风电机组状态模糊综合评估方法。采用不同形式的隶属云(Membership Cloud，MC)发生器估计VT和CT的误差偏差，用混合半梯形MCG处理环境温度引起的误差偏差的不对称性和不规则性。并提出了一种改进的DTW(Modified DTW，MDTW)距离度量误差与影响因素之间的时间序列相似性，以解决DTW中不希望出现的扭曲问题。结合电能表和二次回路的监测误差、CT和VT的估计误差，可以估计出电能计量装置的综合误差水平。该方法可用于电能计量设备的状态监测和严重劣化、故障前的维修需求预测，旨在提高计量设备的可靠性和安全性，提高智能电网的运行效率。通过110 kV变电站电能计量装置的现场试验，验证了该方法的有效性。

1 计量误差影响因素

根据《电能计量装置校准规程》[9]可知，1级、2级计量装置的综合误差分别不大于±0.7%和±1.2%。但是，由于外部环境的影响，操作过程中电能表、VT和CT的误差会有所不同。图1给出了电能计量设备的组成以及不同部分的影响因素。不同影响因素下电能表和二次回路的误差可以通过实时监测得到。

VT和CT的变比和相位误差不能直接连续测量，必须根据变压器的次级负荷和影响因素的实时监测数据进行估计。表1显示了由VT和CT的影响因素(与基本误差限之比)引起的误差偏差限值，其影响因素来自仪表变压器的校准程序。若误差的所有影响因素同时达到最大值，则VT的附加误差偏差将是其基本误差极限的0.87倍，对计量精度有很大的影响。

表1 等效电路验证Tab.1 Equivalent circuit validation

比率误差fI和fU，相位误差δI和δU及它们对VT和CT的主要影响因素如图2所示。其中，I、U、T分别为一次电流、电压和环境温度。采用中国四川某110 kV变电站电能计量设备的现场测试数据，采样间隔为1 min。在图2(a)中，CT剩磁是由一次电流突然损失或二次绕组开路产生的，剩磁可用电流损耗时间tR表示。图2(a)中，电流在t=12时突然降低，此时CT的误差fI和δI突然增加，并且逐渐衰减直至达到正常误差水平。图2(b)则表明VT误差与温度具有一定的相关性，利用误差时间序列与影响因素之间的相似性，可以确定具体的相关情况。

图2 CT和VT的比值、相位误差及其影响因素Fig.2 Ratio and phase errors and influencing factors of CT and VT

2 基于MC的计量误差估计

CT和VT的变比和相位误差可以用外推法计算，但该方法只考虑了二次负载、一次电流和电压的影响。如第二节所述，变压器误差受各种因素的影响，考虑到这些影响因素具有随机性和模糊性的特点，采用MC理论[10-11]描述影响因素对计量误差偏差的不确定性。

2.1 MC理论

MC理论可以实现定性概念和定量值之间的转换。假设μ是一个用精确数字描述的通用集合，C是与U有关的定性概念，假设存在一个数x∈μ随机实现概念C。然后，x对C的映射μ可以定义如下：

(1)

其中u(x)为x对C的隶属度，(x,u(x))的联合分布称为隶属云。MC用一组三个参数描述定性概念：(1)期望值Ex决定MC的平均值；(2)熵En决定MC的变化范围；(3)超熵He决定云滴的分散性。可以通过将云滴数据替换为后向MCG来获取参数。后向MCG依据统计算法将精确数据映射到Ex，En和He的定性概念。对于Ns个xsi样本，这三个参数可以计算为：

(2)

在为随机变量xsi确定Ex、En和He之后，(x,u(x))的MC分布可由前向MCG生成。在MCG中，可用Ex和E′n的参数计算xsi关于C的隶属度μ(xsi)。其中E′n是服从正态分布的随机值，其期望值为En，标准差为He。μ(xsi)关于xsi、Ex和E′n的各种不同函数可产生不同类型的MCG，如对称(正梯形)MCGS、半MCGS和混合MCGS。为了解决影响计量误差的因素的多样性问题，选择半梯形和半正态MCG，并构建混合半梯形MCG量化不同影响因素对VT和CT计量误差的影响。

2.2 温度和频率MC

VT和CT的环境温度允许范围为-25 ℃～55 ℃(额定温度为25 ℃)。在额定温度附近，计量误差不随温度而变化，但在高、低温区，计量误差的变化特征明显不同。因此，提出了一种混合半梯形MC描述环境温度对误差偏差的影响。图3为计量误差随温度变化的MC，由两个表示为C(ExT1，EnT1，HeT1)和C(ExT2，EnT2，HeT2)的半梯形MC组成。当温度在ExT1和ExT2之间时，误差偏差的隶属度为零。在超出该范围的两侧，隶属度可以分别通过相应的MCG进行量化。熵EnT1、EnT2和超熵HeT1和HeT2的混合半梯形MC参数用于表示MC变化范围和云滴分散度。

采用以下步骤来处理用于根据误差偏差生成环境温度的MC分布的混合半梯形MCG算法：

(2)生成正态分布的随机值xT1和xT2，其中xT1～N(ExT1和E′2nT1)，xT2～N(ExT2和E′2nT2)；

(3)重复步骤1和步骤2，直到生成xT1和xT2的K×1组合向量xT及E′nT1和E′nT2的K×1阶组合向量E′nT；

(4)将环境温度xT和E′nT的值代入式(3)可计算出环境温度xT对计量误差偏差的隶属度：

(3)

从步骤(1)～步骤(4)使用前向MCG算法，可以生成(xT,μT)的K个云滴，并绘制相应的误差偏差时温度的MC分布。图3为ExT1=30 ℃，EnT1=10 ℃，HeT1=4 ℃，ExT2=-5 ℃，EnT2=5 ℃，HeT2=1 ℃时的MC分布。式(3)是一个由三部分组成的函数，其中中间部分等于零，而左右部分分别呈现下降趋势和上升趋势，直到分别达到零为止。

因此，图3中的MC分布表现为具有宽顶侧和窄底侧的梯形。左侧区域C(ExT1，EnT1，HeT1)的下降的半梯形MC与右侧区域C(ExT2，EnT2，HeT2)的上升的半梯形MC组合在一起，从而形成图中混合的半梯形MC。

图3 引起误差偏差的环境温度的MC分布Fig.3 MC distribution of ambient temperature on metering error variations

混合半梯形MC的参数很难直接从CT和VT的制造商和铭牌上获得，这些参数可以通过温度的历史样本数据获得。温度数据分为两组：(1)左侧组，其中温度值小于额定温度；(2)右侧组，其中包括所有其他温度数据。ExT1、EnT1、HeT1和ExT2、EnT2、HeT2温的值可以通过将左右两组的温度样本数据代入式(2)中来计算。然后，即可基于混合半梯形MC估计环境温度xTr引起的电能计量误差偏差。当主要区间DT=[xTr-(HeT1+HeT2)/3,xTr+(HeT1+HeT2)/3]内云滴数为L时，环境温度引起的计量误差偏差为[12]：

(4)

式中F=f、δ分别为变比和相角误差，Flim=flim、δlim分别为对应的限值；ηT为误差偏差限值和环境温度的限值，如表1所示。

频率对VT误差偏差的影响与温度相似。当频率在49.5 Hz～50.5 Hz之间时，影响最小，而两端频率范围之外的计量误差偏差是对称的。因此，可以通过对称的梯形MC描述由频率引起的误差偏差。由于误差效应对称性，左、右半梯形MC的熵相等，超熵也相同。利用对称梯形函数作为隶属度，即可实现梯形MC。因此，将式(3)中的下标T替换为F，使得EnF1=EnF2=EnF且HnF1=HnF2=HnF，以实现频率对计量误差偏差的梯形MC。梯形MCG只有四个参数，即ExF1、ExF2、EnF和HeF，在步骤(1)～步骤(4)中，使用前向MCG算法可以生成梯形MC频率分布，其中隶属度函数应采用上述对称梯形函数。与式(4)类似，由监测频率引起的计量误差偏差可以基于对称梯形MC估计。

2.3 其他影响因素的MC

外电场、磁场、高压泄漏电流引起的电压互感器、电流互感器计量误差变化趋势基本一致。由于电压互感器的误差随电场变化，外加电场对测量误差的影响是电场增强的结果[13-14]。图4中，VT的计量误差随外电场的变化可以用表示为C(ExE，EnE，HeE)的上升半梯形MC来描述，估计外电场引起的计量误差偏差的计算过程与前一节类似，其中MC分布应由电场的上升半梯形MCG产生。在半梯形MC中，μE(xE，E′nE)的隶属度函数可以表示为：

图4 外电场测量误差的MCFig.4 MC of metering error with external electric field

(5)

式中xE和E′nE为电场云滴及其标准偏差的正态分布随机值。式(5)是一个有两个部分的分段函数，其中右段等于1，而左段从0上升到1。这就导致隶属度从分散上升趋势变化到图中某个区间内的持续饱和。

电流互感器铁芯中的剩磁可能是由于电流骤减和二次绕组开路引起的，降低了铁芯的磁导率，影响了互感器的精度[15]。随着时间的推移，剩磁的直流分量逐渐向零衰减，对CT误差的影响也随之减小。因此距最新电流损耗的时间tR可用于表示剩磁效应。

图5中，剩磁对测量误差偏差的影响由表示为C(ExR，EnR，HeR)的下降半正态MC来描述。当tR时，误差偏差最大，且随tR的增大而逐渐衰减。估计剩磁引起的误差偏差的计算过程与前一节类似，其中MC分布是由下降的半正态MCG产生的。下降的半正态MC的隶属度函数μR(xR，E′nR)表示为：

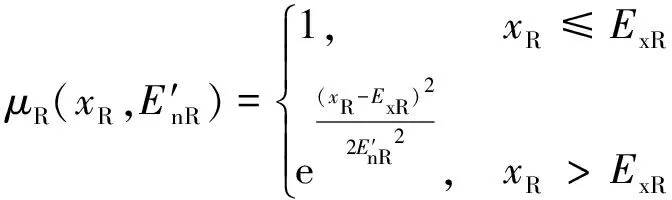
(6)

式中xR和E′nR分别为剩磁云滴及其标准差的正态分布随机值。剩磁的半正态MC与半梯形的MC不同，前者的ExR=0，因此在没有饱和间隔的情况下，存在分散下降趋势，如图5所示。由于E′nR的标准偏差由正态分布表示，其期望值和标准偏差分别为EnR和HeR，因此MC可以考虑云滴的分散性。

图5 剩磁测量误差的MCFig.5 MC of metering error with remanence

3 计量误差和影响因素之间的相似性

在估计各在线监测影响因素引起的计量误差偏差后，必须综合各因素的误差偏差，才能得到VT和CT的总误差偏差。根据计量误差时间序列与影响因素的相似性，采用加权法求出综合误差。由于在当前时刻之前的历史计量误差数据是可用的，因此必须根据最近的计量误差历史数据和上一时间间隔内的影响因素来计算相似度。

DTW方法是一种基于内容强度和结构信息的相似度测量方法，由历史时间序列本身提供。 它不依赖于与不同时间序列相对应的状态变量之间的隐式交互模型。因此，DTW方法可用于度量计量误差与温度，电场，频率，磁场，剩磁和漏电流等影响因素的相似性。由于DTW方法完全是由数据驱动的，并且不依赖于上述影响因素不同的MC模型，因此可以通过相同的DTW程序逐一计算每个影响因素的相似度。

DTW方法的挑战在于找到使动态规整距离之和最小的最优路径[16]，假设计量误差偏差的时间序列为x={x1,x2,…,xm}，长度为m；VT的影响因素为yX={yX1,yX2,…,yXm}，长度为n，X=T、E、F和M分别表示温度、电场、频率和磁场。CT的影响因素为yY={yY1,yY2,…,yYn}，Y=R、T、M和C分别表示剩磁、温度、磁场和漏电流。尽管影响计量误差的因素的非线性相互作用可能会在历史时间序列中产生不确定的干扰，但在不同的时间序列中干扰相对较小且均匀，DTW对这种均匀分布的数据噪声具有很好的容忍性。

因此，基于DTW的相似度测量对于各种影响因素同样有效，以x中的计量误差和yY中的CT影响因素为例，图6为DTW的原理，从图6(b)的起点(x1,yY1)到终点(xm,yYn)搜索规整路径w={w1,w2,…,wK}，其中，wK表示距离D(xi,yYj)=|xi-yYj|，wopt的最优规整路径可以选择为使DDTW沿该路径的累积距离最小。

(7)

DTW通过时间序列中的点的自我复制，实现图中两个时间序列的匹配。但水平或垂直方向上点的过度自我复制可能会导致图6(a)中的短片段和其他相对较长的片段之间出现不切实际的匹配。为了克服这个缺点，在经典的DTW中引入了斜率约束条件，然后，可以通过限制图6(b)中任意点的连续自我复制次数获得修改的规整路径。MDTW规整路径受到以下约束：

图6 时间序列的DTWFig.6 DTW of time series

(1)规整路径的边界条件：w={w1,w2,…,wk}，w1=D(x1,yY1)，wk=D(xm,yYn)；

(2)单调条件为：当wk-1=D(xi′,yYj′)且wk=D(xi,yYj)时，i-i′≥0，j-j′≥0且i-i′+j-j′≠0；

(3)连续条件：当wk-1=D(xi′,yYj′)且wk=D(xi,yYj)时，i-i′≤1，j-j′≤1；

(4)斜率限制条件为：

(8)

式中Cxm和Cyn为垂直方向(i-i′=0)和水平方向(j-j′=0)的自我复制时间；Clim为连续时间的极限；S为相对于极限的斜率系数。图7给出了不同斜率限制条件下规整路径的可行区域。当斜率系数S=0时，规整路径被限制在对角线上，无法传递到终点(xm,yYn)。S范围越大，意味着可以有更宽的规整路径覆盖可行的区域。 当S=∞时，对规整路径的斜率不加限制。

S<1和S<2/3的可行域如图7所示，其中参数Clim=3；规整路径不能有过度的平缓和陡坡，这些偏差会导致不希望的时域翘曲出现，如图6所示。虽然规整路径斜率可以通过引入斜率条件加以限制，但当斜率条件过于苛刻时，时间序列之间的匹配效果并不理想。

图7 斜率受限的条件和禁区Fig.7 Slope-restricted condition and forbidden area

此外，如图6(b)所示，式(8)中的斜率系数在0≤S<1的适当范围内，因此可以防止不希望的翘曲，还可以减少搜索路径的数目。由于式(8)中的斜率条件，修改后的规整路径不能覆盖的禁止区域如图7所示。禁区的点应忽略，因为它们位于不希望出现的翘曲路径上。根据斜率限制条件，可将禁区中的Db内的点集写为：

(9)

「·⎤是一个上限函数。由于最佳规整路径的累积距离最小，所以用相对较大的常数Dmax代替Db禁区中的距离D(xi,yYj)，以避免将禁区的点搜索到最佳规整路径中。然后，将点(x1,yY1)到点(xi,yYj)在MTTW最优规整路径中的累积距离定义为C(i,j)。则累积距离C(i,j)的递推公式可以导出为：

C(i,j)=D(xi,yYj)+ΔD

(10)

式中ΔD为点(xi,yYj)之前的累积距离，取决于Cxm和Cyn在垂直和水平方向上的连续自我复制时间。不同连续自我复制次数下的ΔD公式见表2。根据式(10)中的递推公式，可以搜索MDTW的最佳规整路径以实现最小的累积距离，得到DMDTW的解为：

表2 不同的规整路径下的累积距离Tab.2 Accumulate distance under different warping paths

DMDTW=C(m,n)

(11)

根据第1节图2(a)的现场试验数据，采用MDTW法计算计量误差与影响因素之间的距离。图8显示了计量误差与CT的影响因素的相似性，包括剩磁yR、温度yT、磁场yM、漏电流yC和一次电流I。MDTW距离越短，计量误差和相应的影响因素之间相似性越大。图8表明，CT计量误差与温度、漏电流和磁场的相关性最小，但与剩磁(用电流损失时间tR表示)和不同时间一次电流I的相关性很高。在电流损耗过程中(t= 0.2 h-0.9 h)，误差偏差更接近于剩磁的影响因素，而在其他时间间隔内，计量误差主要与一次电流有关。

图8 CT相似性Fig.8 Similarity of CT

根据图2(b)中的测试数据，比较MDTW和DTW性能，图9给出了VT变比误差与影响因素之间的相似性。影响因素包括磁场yM、频率yF、电场yE、温度yT和一次电压U。图9表面，误差与磁场、频率，一次电压的距离比温度和电场的大，这是因为前者的影响因素几乎没有太大的变化，并且保持在额定值附近。

此外，在测试情况下，计量误差的偏差更多地依赖于温度而不是电场，如图9所示，温度和电场之间的MDTW距离之差大于DTW,结果表明，MDTW能更准确地识别不同影响因素对计量误差的影响差异。

图9 MDTW和DTW的VT相似性Fig.9 Similarities of VT by MDTW and DTW

4 综合计量误差估计

利用影响因素和相应MCG的连续监视数据，可以计算VT的FTU、FEU、FFU、FMU，它们分别代表由温度，外部电场，频率和磁场引起的误差偏差。此外，还可以得到CT的FRI、FTI、FMI、FCI，它们分别代表了剩磁、温度、磁场和漏电流引起的误差偏差。根据变压器的历史数据，得到电压互感器(VT)与电流互感器(CT)误差的相关性及影响因素。根据外推法基于二次负载、一次电流和电压基础上的VT和CT的基本误差FSU和FSI，可以计算出其他影响因素以及VT和CT计量误差引起的误差偏差为：

(12)

(13)

式中 ΔFU和ΔFI分别为VT和CT的综合误差偏差；DTU、DEU、DFU和DMU、DRI、DTI、DMI和DCI为MDTW距离；ΓTU、ΓEU、ΓFU和ΓMU、ΓRI、ΓTI、ΓMI和ΓCI为基于MDTW距离的加权系数的符号(正或负)。符号系数表示影响因素对误差偏差的正负影响。对于来自同一制造商的相同类型的VT和CT，附加误差偏差和影响因素之间的相关性(包括MDTW距离和符号系数)是稳定的且一致的，这一结果可以通过相同内部结构和类型的变压器材料以及相同的校准程序和要求来保证。符号系数的计算可以表示为一个整数线性规划问题，最优问题公式如下：

(14)

(15)

式中fU、fI、δ′U和δ′I为VT和CT的误差测试数据，fSU、fSI、δSU和δSU，ΔfU、ΔfI、ΔδU和ΔδU分别为基本误差和综合误差偏差的估计结果。式(14)和式(15)的符号系数模型可以用分枝定界算法求解，然后通过式(12)和式(13)即可VT和CT的估计误差。

在电能计量系统中，三相三线制和三相四线制分别有两对和三对VT和CT。在同一电能计量系统中，不同变压器的精度特性和误差偏差特性与影响因素基本相同。因此，可以利用不同电压互感器和电流互感器的二次负载、一次电流和电压来计算fSU和fSI，然后通过添加积分误差偏差量ΔfU和ΔfI来获得它们各自的变比误差fIi和fUi以及相位误差δIi和δUi，其中i=1～3表示系统中不同的变压器对。结合电能表的监测误差γb，以及不同电压互感器二次回路的变比和相位误差fdi和δdi，将电能表的综合计量误差表示为：

γ=γb+γh+γd

(16)

式中γb、γh、γd分别为电能表、变压器和二次回路的计量误差。对于三相三线(两对VT和CT)电能计量设备，γh和γd为：

(17)

式中φ为主要负载的功率因数角。对于三相四线(三对VT和CT)电能计量设备，γh和γd为：

(18)

二次回路的变比和相位误差fdi和δdi分别是VT二次回路的相对于幅值的电压降落值和相角误差。基于fdi、δdi和φ，以fIi、fUi、δIi、δUi表示的电能计量误差γh的公式为现场校准公式，估计出的综合计量误差可用于监测电能计量设备的整体状况和计量误差的修正。此外，由不同来源的电流互感器、电压互感器和二次回路估计出的误差可以用来跟踪误差来源，支持电能计量设备的状态维护。

5 现场试验

图10所示的电能计量设备的现场试验是在四川的一个110 kV变电站进行的。

图10 电能计量系统现场试验Fig.10 Field test of electric energy metering system

通过变电站，10 kV中压配电网连接到110 kV高压配电网。由于高压计量设备的精度等级要求比中压计量设备的精度等级要求更高，因此对高压计量设备的测试可以更有效地验证该方法。利用电能计量误差监测系统记录电能计量误差及其影响因素。CT和VT监视器的数据由电能表和二次回路监视器采集，然后再传输到工作站(数据记录器)。多个电能表应通过集中器与其他设备连接。

图11为根据图2(a)中的测试数据由CT影响因素引起的误差偏差及其变比和相位误差。CT在t= 12 min时失去电流，然后fRI和δRI误差急剧增加，而误差随温度，磁场和泄漏电流的变化在图11(a)中没有显著变化。为验证所提方法的有效性，将一组相同的计量设备用作对比样品，其输入电压和电流由可编程标准源提供，这些标准源跟踪测试样品的实时数据，并且可以通过实验校准平台测量计量误差。图11(b)给出了通过测量，外推和所提方法得出的CT误差结果。由于外推法仅考虑了初级电流和次级负载的影响，因此其fSI和δSI与测量结果不一致。

图11 CT影响因素和估计误差引起的误差偏差Fig.11 Error variations caused by influencing factors and estimated errors of CT

在图11中的整个过程中，计量误差和CT影响因素之间的MDTW距离为DRI=0.0821，DTI=0.3694，DMI=0.1692，DCI=0.4211，这表明计量误差偏差是由于剩磁引起的。所提出的方法(MCG-MDTW)的误差趋势与测量结果相似，这一发现证实了所提方法是有效的。图12中的VT计量误差是根据图2(b)中的测试数据通过不同方法计算得到的，在这种情况下，影响因素不会表现出明显的突变，因此三种方法的变比和相位误差相似。与外推法相比，MCG-MDTW相位误差和测量结果更加一致，因此，该方法具有更好的适应性。

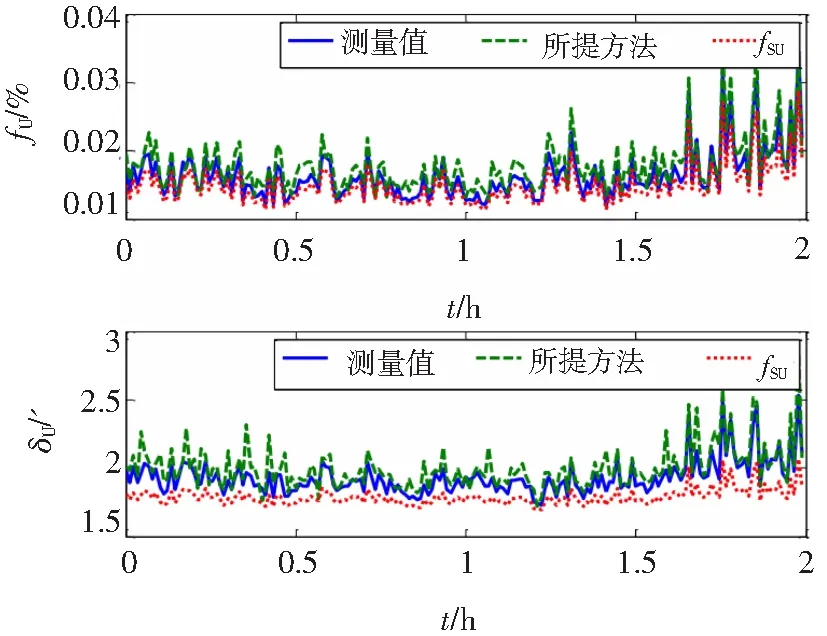
图12 估计VT误差Fig.12 Estimated VT errors

使用外推法、MCG(fSI和δSI直接加上MCG计算的误差偏差)、MCG-DTW(用DTW代替MDTW)和MCG-MDTW方法估计的综合误差如图13所示。综合电能表误差、VT和CT的估计误差以及VT二次回路的电压降，根据式(16)和式(18)计算综合误差。为了比较不同方法的性能，表3中提供了估计和测量结果之间的归一化均方根误差(NRMSE)和归一化最大幅值误差(NMAE)。NRMSE和NMAE越小，对应的方法性能越好。MCG，MCG-DTW和MCG-MDTW方法的NRMSE分别为18.9495%，18.3619%和10.4084%，小于外推法的34.6654%。

图13 不同方法的综合误差估计Fig.13 Estimated comprehensive errors of different methods

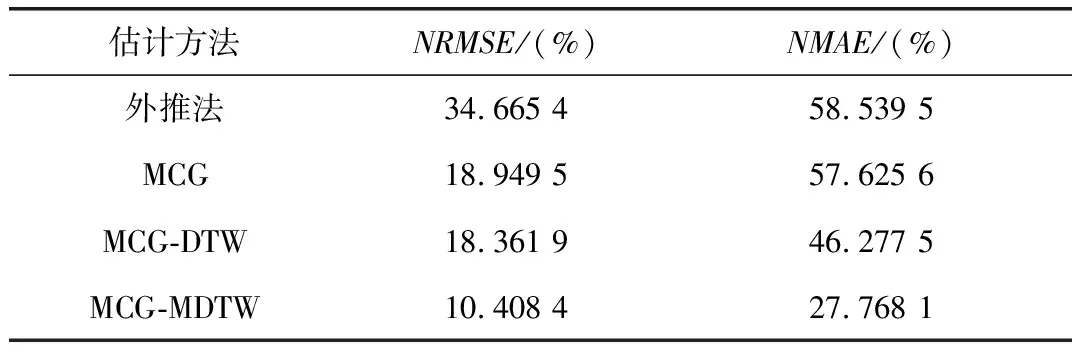
表3 不同方法的性能指标比较Tab.3 Performance index comparisonof different methods

MCG-DTW的性能几乎与MCG相似，但都比MCG-MDTW方法差。这一发现表明，MCG-DTW方法不能改善由不同影响因素引起的误差偏差的积分，因为DTW距离出现了不希望出现的翘曲。用不同方法估计CT和VT(三台变压器的平均值)的综合误差、变比和相位误差的NRMSE如表4所示。所提出的MCG -MTTW方法的最大NRMSE在各种误差源中为13.85%，仍然比其他方法的最小NRMSE 15.25%小。这种比较表明，与MCG-DTW，MCG和外推法相比，所提的MCG-MDTW方法更有效，该方法不仅可以通过MCG估计出影响因素的误差偏差，而且可以采用MDTW距离作为加权误差偏差量。表4表明，所提方法对于不同误差源的性能优于MCG-DTW方法。

表4 估计综合误差、CT和VT误差的NRMSETab.4 NRMSE of estimated comprehensive error, and CT and VT errors

6 结束语

文中提出了一种基于MCG和MDTW的电能计量误差估计方法。该方法可用于电能计量设备的状态监测，以检测潜在的故障，纠正计量误差。利用110 kV变电站现场试验数据对该方法的应用进行了验证。该方法的主要优点是可以量化不同影响因素对计量误差的不确定性和它们之间的相似性，从而实现误差随输入条件和外部环境的变化。通过增加斜率条件，使得MDTW的相似性分析方法更适合于现场试验中的小样本数据。实验结果表明，MCG与MDTW相结合的方法在有效性和适应性方面明显优于外推法、MCG法和MCG-DTW法。估算结果可用于评价电能计量设备的健康状况，还可用于开发更智能的计量设备维护和更换计划，从而降低运行和维护成本，提高电力系统的管理效率。