基于护栏性能指标的集成式人工智能模型研究
涂晓威,雷正保
(长沙理工大学 汽车与机械工程学院,湖南 长沙,410114)
公路安全护栏作为一种常用的交通基础设施,能够通过自身结构的变形对事故车辆起一定的缓冲能力,确保碰撞最大加速度在安全范围内并且能够实现对车辆的重新导向,同时防止车辆碰撞到道路旁的固定物,如树、电线杆等。而随着当今道路交通的不断发展,也要求护栏具有更高的防护能力,因此对于护栏进行优化设计具有重要的意义[1]。以波形梁护栏为例,护栏设计中主要需要考虑受到冲击后波形板、防阻块和立柱的自身形变等,因为护栏各部件结构尺寸将直接影响护栏的防护能力。而在以往的护栏优化设计中大部分是基于设计经验和真实的汽车护栏碰撞数据进行结构优化[2],少有系统化的优化设计方式,其主要原因在于护栏部件的几何尺寸与各评价指标之间的高度非线性关系。目前有限元仿真在护栏相关研究中被广泛应用,能极大地减少护栏设计的成本与时间,赵建等[3]利用有限元仿真与正交设计结合得到基本样本,再将尺寸因素与性能指标结合进行极差、方差和贡献率等参数分析,得到较优参数组合以实现护栏优化设计的目的。随着机器学习在各个领域的广泛应用,同样有研究者将代理模型与优化算法相结合进行护栏设计,Yin等[4]使用径向基函数(RBF)与多目标遗传算法(NSGA-II)对护栏防阻块厚度和η型护栏的柱弓长度尺寸进行优化,Hou等[5]利用代理模型与多岛遗传算法(MIGA)对立柱间距和波形梁板厚度进行了尺寸优化以提高护栏防护性能,上述研究中的一个关键点在于预测模型的准确性将直接影响护栏设计的复杂性和准确度,但目前对于护栏性能预测没有具有明显优势的预测模型,而人工智能模型有着强大的解决非线性问题的能力,但大多数的研究中均是对单一模型进行少量优化来增强模型性能以提高预测效果,而Chou等[6]对比不同人工智能模型在高性能混凝土抗压强度预测上的应用结果,发现复合模型预测精度和稳定性高于单一模型。因此本文提出一种用于护栏防护性能指标预测的高性能集成式的强化人工智能模型,使其能对护栏设计起指导作用。
1 模型搭建方法
本文中使用IBM SPSS modeler进行模型的训练和集成,各个模型基本参数选用默认值,并结合十折交叉验证方法来提高模型的可靠性,选用的单个初始模型分别为支持向量机(SVM)、广义线性回归(Genlin)、径向基人工神经网络(RBFNN)、反向传播神经网络(BPNN)和分类与回归树(CART)模型。对各训练完成后的模型使用预留数据样本进行预测效果对比,选用其中较优的模型用于后续的集成模型构建。
1.1 模型基础理论
1.1.1 SVM
Vapnik[7]首先提出了SVM模型,该模型可应用于分类和回归问题,在解决非线性问题时可以将特征参数映射至高维空间中,再使用非线性核函数构造并求解二次规划问题。

式中,ω为权重;b为常数项;φ(·)为非线性方程,它将特征参数映射到更高维空间中, ·,·表示在Rn内的点积。
SVM使用ε的不敏感损失函数来度量结构的风险,寻求风险性最小化,因此可以将其转化为式的最小化问题:

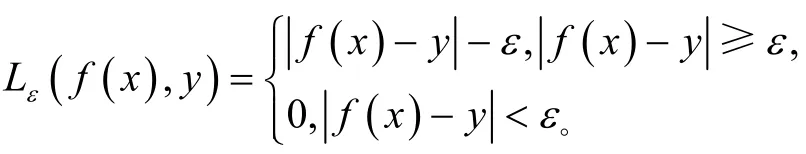

上述的优化问题可以通过拉格朗日乘数转化为二次优化问题来处理,转化为式:


1.1.2 Genlin
Nelder和Wedderburn[8]提出Genllin模型以使用连接函数来反应线性预测值和响应变量期望之间的关系,其较一般线性模型更为灵活,允许响应变量存在误差。Genlin模型中包含随机部分、系统部分和连接部分,随机部分为响应变量Y的概率分布(如正态、泊松、伽马、二项和逆高斯分布等),系统部分为线性组合模型,连接部分中连接函数g(·)将Y的期望值连接到预测值η。
该模型可由式定义:

式中,其中η是线性预测值;O是偏移变量;Xi是自变量;βi是斜率系数;F是Y的分布。
1.1.3 BPNN
人工神经网络(ANN)是通过模拟人脑中的神经元,多层元素交互并行连接而成,可以用于得到复杂非线性问题中的内部隐藏关系。反向传播神经网络(BPNN)是其中被广泛使用的一种,其包含输入层、隐含层和输出层,其通过不断反向传播,根据误差项调整神经元之间的连接权重来增强模型效果,隐含层的输出如式所示:

式中,netk是第k个神经元的激励值;j为前一层神经元目的序号;wkj为第k个神经元与前一层第j个神经元之间的连接权重;oj为第j个神经元的输出;f(·)为激励函数,常用sigmoid函数,如式所示:

每个周期中对于权重wkj的更新如式所示:

式中,t表示当前周期序号; Δwkj(t)表示改变量,通过式表示:

式中,η为学习速率参数;δpj为传播误差;α为动量参数。
1.1.4 RBFNN
RBFNN是由Broomhead和Lowe[9]提出的一种人工神经网络,其与BPNN不同,其隐藏层为RBF神经元,是一种局部逼近神经网络。其隐藏层是标量权重和输入向量的线型组合,这些向量通过每个节点中的径向基函数进行映射,输出层生成向量RBFNN的输出可表示为式:

式中,m为输出数目;wjp为第j个基函数和第p个输出节点之间的连接权重;是径向基向量,使用高斯函数表示为式:
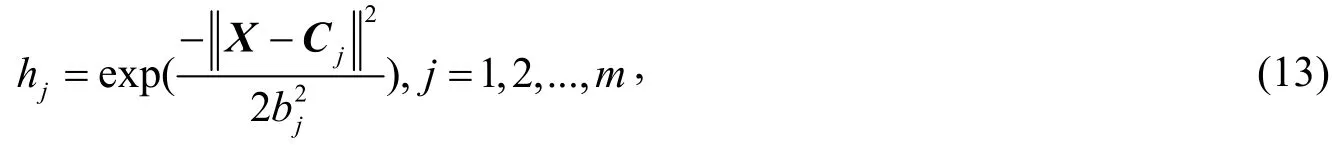
1.1.5 CART
CART是Breiman等[10]提出可用于回归和分类目的的递归划分方法,其为二叉树,其中包括根节点、中间节点和终端节点。回归树是通过遍历变量j和对应切分点s,使得式值最小从而得到最优切分变量j和切分点s。
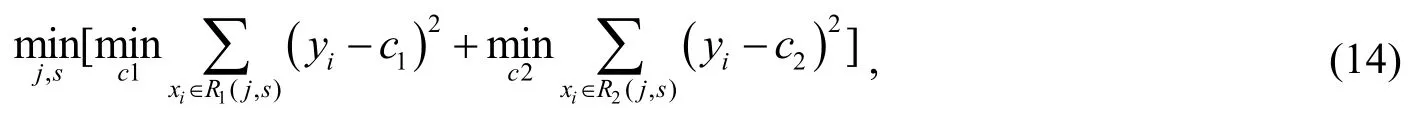
式中,R1(j,s)和R2(j,s)表示由切分点s得到的2个特征空间,其中c1和c2为两个特征空间中输出y的均值,如式所示:

最终得到回归树模型如式所示:

式中,M为空间划分区域数目;Rm为拆分后的特征空间;cm为对应特征空间的输出;I为判别系数。
1.2 集成模型的搭建
使用IBM SPSS modeler对上述单个模型进行建模后,对数据集进行处理,除一部分样本作为后续的检验样本外,其余样本根据十折交叉验证方法,随机分为10组,在每次训练中将其中9组作为训练集,余下一组作为测试集,共经过10轮次训练,且每次模型训练过程中的训练集和测试集都与其他轮次中不同,将其中预测效果最佳的一次模型作为最后训练所得模型,用于后续的模型对比和集成模型搭建。
对于使用同一个数据集训练得到的这些单个模型,挑选出其中最优的3种模型进行集成,从而得到4种集成模型,其集成方法在数学上的表示为对应于d维预测变量X和一维响应Y。各指定的算法均生成一个估计函数f(·),而集成函数fe(·)是通过各单个函数的线性组合获得的,如式所示:

式中,n为估计函数个数;ci为估计函数fi(·)的线性组合系数。

式中,fe(·)为集成模型,X为d维预测变量,表示护栏的几何尺寸组合,Y为一维响应,本文中为加速度值。
综上,集成模型的搭建流程如图1所示。后续将使用上述预留检验样本来对所有模型进行预测效果的探究。
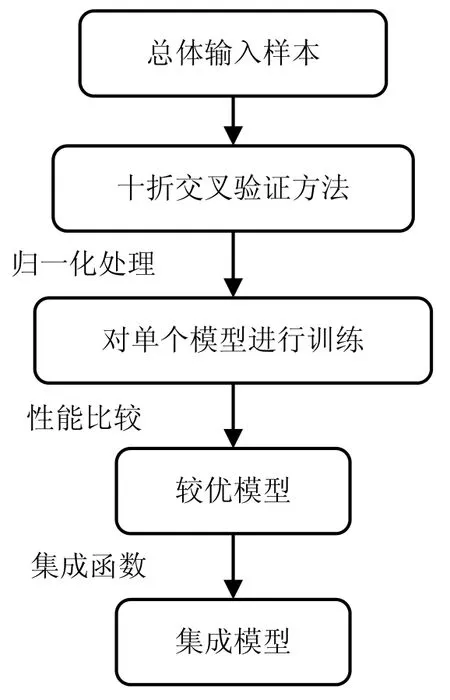
图1 集成模型搭建流程图
2 数据准备及模型评价指标
2.1 数据来源
现有法规中对于护栏的评价指标有多个方面[11],加速度值是其中十分重要的性能指标,为了更好的进行对比,数据集中的护栏评价指标均为加速度。为了保证本文中的模型对比具有可靠性,本文采用的数据均来自现已发表的文献,且这些文章中所用模型的有效性均在原文中得到验证。
数据集1由Yin等[4]研究所得,该研究中主要以RBF模型为基础,以η型波形梁护栏为研究目标,使用波形板厚度t和η型立柱外伸长度L两个特征参数对护栏性能指标进行预测(特征参数对应至护栏结构的示意图如图2所示),该研究中将碰撞过程中车辆的质心加速度换算得到的乘员的最大加速度值作为重要指标。其中样本集采用全因子设计所得。

图2 数据集1对应的护栏整体及特征参数
数据集2由Hou等[5]研究所得,该研究主要是对护栏立柱间距x1和波形梁板厚度x2对护栏整体性能的影响进行了研究(特征参数对应至护栏结构的示意图如图3所示),文中使用超拉丁立方采样方法构建样本集,使用RBF-MQ模型对车辆碰撞过程中的质心加速度值进行预测。

图3 数据集2对应的护栏整体及特征参数
2.2 模型评价指标
为了评估预测模型的准确性,各研究中均使用了相应的模型预测评价指标,数据集1的对应研究中,研究者采用最大相对误差绝对值(MARE)和均方根误差(RMSE)作为评价指标,可以分别通过式和得到:

式中,y为实际加速度值;y′为预测加速度值。

式中,n为样本数目,i= 1 ,2,...,n;y为实际加速度值;y′为预测加速度值。
数据集2对应研究中同样使用了MARE值作为评价指标之一,另一个评价指标为相对平均绝对误差(RAAE),可以通过式得到:

式中,n为样本数目,i= 1 ,2,...,n;y为实际加速度值;y′为预测加速度值。
为了综合多个评价指标来反映各模型的预测准确性,本文中提出使用综合满意度(CS)来对比在相同数据集的输入下不同模型的预测性能,可以通过式得到:

式中,m为评价指标数目,i= 1 ,2,...,n;Ii为某个模型的评价指标i的值;min(Ii(x) )为所有模型评价指标值中的最小值;max(Ii(x) )为所有模型评价指标值中的最大值。
在后续的预测对比中,不同模型使用某一数据集进行对比时,使用与该数据集来源文献中的相同评价指标进行对比,并增加CS值作为综合评定指标,CS值越接近于0,表示对应模型的预测效果越好。
3 模型对比分析
在本节中,将对上述选用的5种单个模型的预测结果进行比较,后续再将该结论与集成模型的预测效果进行比较。
3.1 试验结果
如表1所示,根据模型预测评价指标(18)-(21)对各单个人工智能模型的预测结果进行了对比。由表1可知,对于数据集1,BPNN模型、RBFNN模型和Genlin模型的CS值分别为0、0.399和0.553,优于其他2种模型,因此将使用这3种模型用于后续的集成模型搭建。由表2可知,数据集1对应的4种集成模型中性能最优的为RBFNN+BPNN+Genlin模型,其MARE和RMSE值也优于对应的3种单个模型,具有更好的预测性能。而对于数据集2而言,Genlin、BPNN和RBFNN模型的综合性能较优,CS值分别为0.011、0.023和0.490,相应的可以得到表2中的各数据,其中RBFNN+BPNN+Genlin模型的MARE值和RAAE值优于其他集成模型和其对应的3种单个模型。
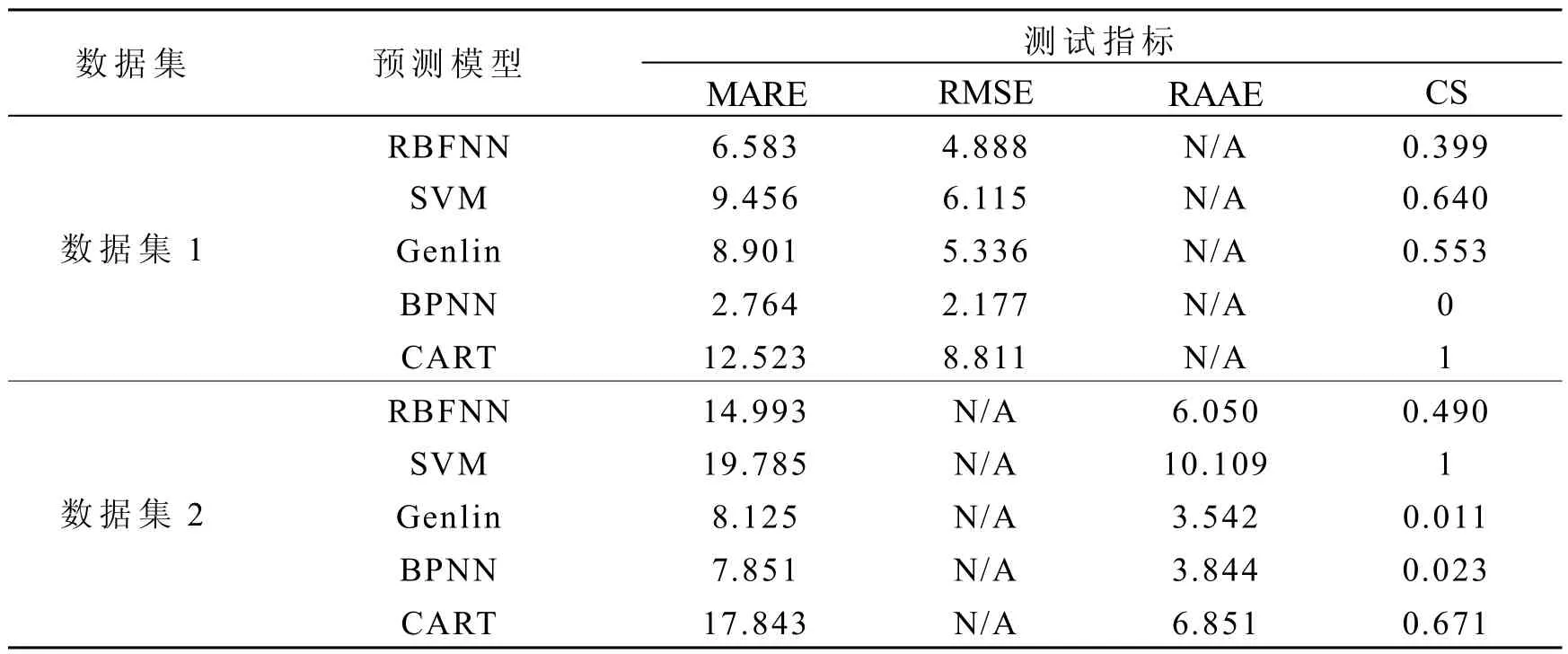
表1 单个模型性能对比
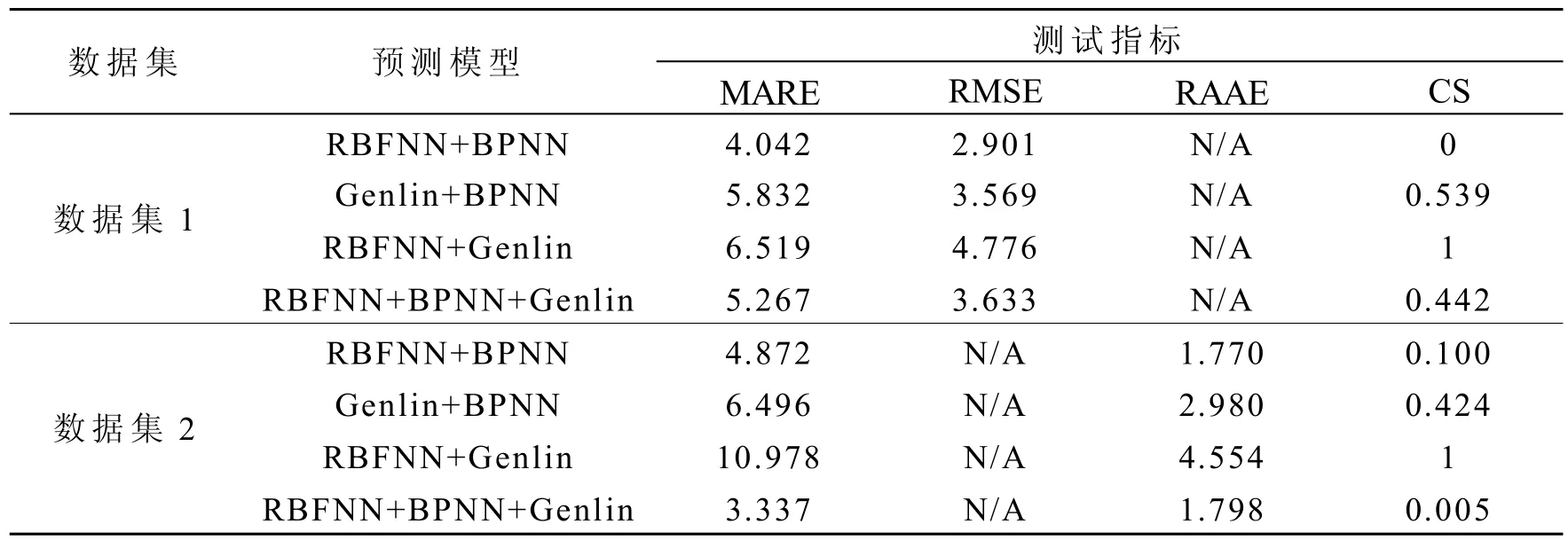
表2 集成模型性能对比
3.2 模型比较
近年来,许多学者也开始使用机器学习来协助护栏设计,而提高模型预测精度则是能够有效提高开发效率的重点,因此本文中将根据表1和表2的结果,将其与对应数据来源文章中所提出的预测模型进行比较。各数据集中研究者使用的最终模型的性能指标值如表3所示,数据集1对应的研究者使用RBF模型进行护栏性能预测,并使用MARE和RMSE作为性能指标,其结果分别为8.790和4.754,数据集2对应的各项数据为研究者使用RBF-MQ模型得到,并以MARE和RAAE作为评判指标。

表3 数据来源研究中所用的模型性能
使用各对应数据集进行预测,原文章所使用模型、最优单个模型和最优集成的预测精度对比如表4所示,由表4可知,集成模型具有更高的预测精度,各项模型指标值(MARE、RMSE、RAAE)降低24%~58.9%。以数据集2为例,集成模型(RBNNF+BPNN+Genlin)的MARE和RAAE值较单个模型降低58.9%和49.2%,较原文中的预测模型降低24.2%和36.9%。

表4 集合模型的性能提升比例
由表3和表4可知,集成模型具有更高的预测性能,与之前的研究不同,本研究使用了十折交叉验证方法来确保模型具有良好的泛化能力,因此使用决定系数R来验证模型的可信度[6],由式可得。

式中,n为样本数目,i= 1 ,2,...,n;y为实际加速度值;y′为预测加速度值。
各组数据集对应的最优单个模型、集成模型和原文中所用模型的决定系数对比如图4所示,集成模型的决定系数均大于0.9,且最优集成模型的决定系数最接近1,因此表明所得的模型具有较高的可信度,并且结合上文中的结论,本文中提出的集成模型的预测准确性优于目前相关文献研究中所用模型。
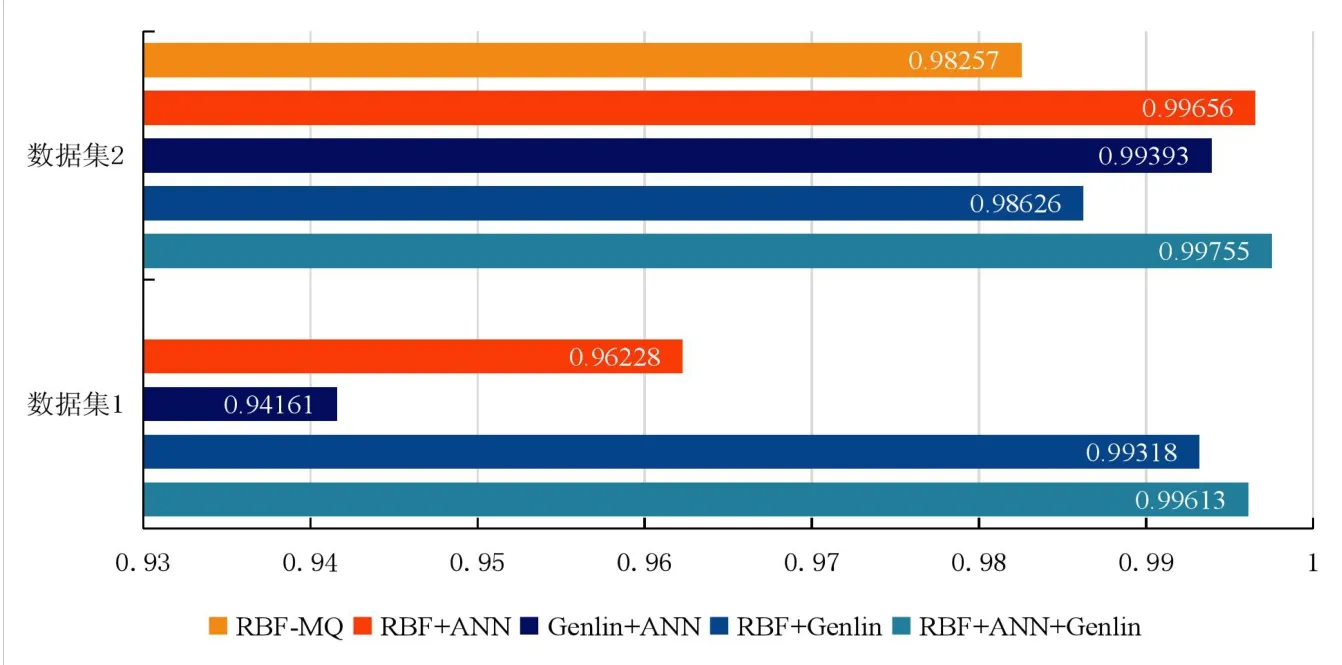
图4 各数据集对应模型决定系数对比
4 结论
本文针对目前缺少一个具有明显优势的高精度和高泛用性的预测模型来形成系统的高效护栏设计方法这一问题,引入集成式人工智能模型来进行护栏性能的预测,高性能预测模型配合优化算法能够极大地减少护栏设计成本并系统化设计方式,具有很强的工程意义。在本文中主要对集成模型性能方面进行了探究。
文中对单个模型训练时使用了十折交叉验证方法,提高了模型的泛化能力,并通过综合满意度对单个模型性能进行了判断,挑选出较优单个模型并使用集成函数得到集成模型。通过使用现有研究中的数据集对集成模型在护栏性能预测方面的有效性进行了验证,再通过对比单个模型、现有研究中的模型和集成模型,发现集成模型具有明显优势,RBFNN+BPNN+Genlin模型各项指标值较现有研究中所使用模型提升24%-58.9%,具有更强的鲁棒性和更高的预测精度。

