基于RCMDE的2D80-53.4型压缩机故障诊断研究

曲孝海,胡予欢,沈磊

(湖南文理学院 数理学院,湖南 常德,415000)

2D80-53.4型压缩机是典型的石油机械[1-2],由于2D80-53.4型压缩机工作环境恶劣,工作强度高,导致压缩机中轴承极易在这种环境下产生磨损故障。因此对压缩机轴承故障诊断变得非常重要,为了有效地提取故障的特征信息,提高故障诊断精度,提出了基于RCMDE的2D80-53.4型压缩机轴承故障诊断方法。

近些年来,非线性、非平稳信号分析理论发展迅速,Uhlmann A将热力学中的信息熵算法引入时间序列对其进行复杂度衡量[3]。基于Uhlmann A的研究,众多学者发展了度量时间序列不确定度的多种熵值算法;Pincus[4]等为更准确地反映整体系统复杂性提出了近似熵算法;通过引进多尺度对时间序列进行复杂度分析,Costa等[5]提出了能够综合时间序列的熵值算法——多尺度熵;Hamed Azami等[6]考虑到时间序列振幅之间的关系,提出了一种具有高效计算速度的散布熵(Dispersion Entropy,DE);Hamed Azami[7]等借鉴多尺度熵思想,结合新型熵值算法散布熵提出了多尺度散布熵多样本数据进行特征向量构建。

针对传统的散布熵在含有混合噪声的故障诊断中存在特征提取效果差等问题,提出将多尺度和精细复合的思想与传统散布熵结合,构建精细复合多尺度散布熵[8],本文将精细复合多尺度散布熵应用于2D80-53.4型压缩机并对其实现智能诊断研究。

1 精细复合多尺度散布熵

1.1 多尺度熵

多尺度熵是通过引入多个时间尺度对原序列进行特征分析,其计算原理如下。

设时间序列u(i)={u(1),u(2),…,u(N)},对其进行多尺度化的过程如式(1)示。

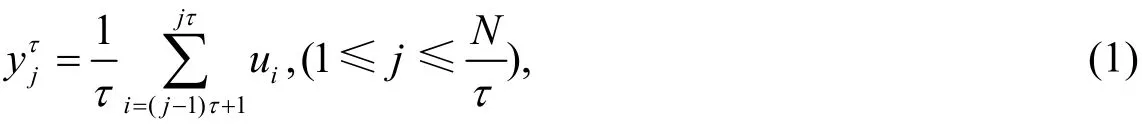
式中:τ表示尺度因子,是对原序列进行具体划分的依据。具体尺度化步骤如图1所示。

图1 具体尺度化过程图

1.2 多尺度散布熵

多尺度散布熵是通过将多尺度方法引入传统熵值算法得到的一种新型熵值算法,较原散布熵有更好的特征提取精度及稳定性。 MDE熵值算法的计算过程如下:

对原信号数据u={ui}进行数据重构,对原数据中依次取尺度因子的数据进行平均化,计算式为

(1)将xj(j=1,2,…,N)映射到[1,c]范围内的c个类别中。将x映射到[1,c]的y={y1,y2,…,yN},其表达式为

其中:σ=Std(X),μ=E(X)。

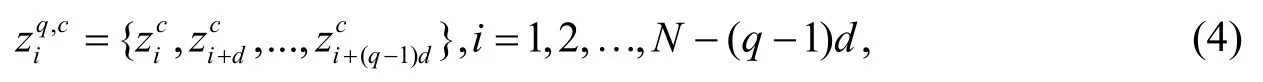
(4) 根据熵值定义求得散布熵熵值为

(5)引入多尺度计算得到多尺度熵熵值为

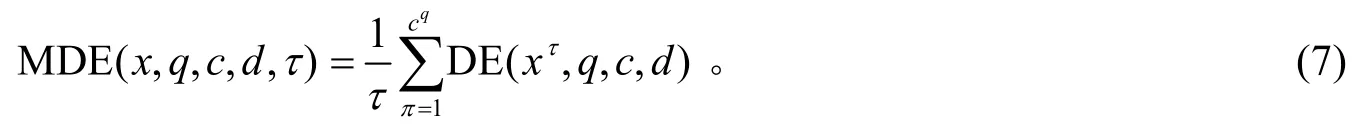
1.3 精细复合多尺度散布熵

由多尺度散布熵计算原理可知,粗粒化过程中遇到时间序列过短容易引起无定义熵值情况,从而影响熵值的计算结果,为解决此问题,引进精细复合思想,构建了RCMDE熵值算法,

精细复合多尺度熵的核心是先计算出所有尺度下的时间序列,然后再计算熵值,其能够很好地减少无定义熵值概率,并且能够适应短序列数据样本。

2 仿真分析

为验证本文方法的优越性,通过随机构建一个常见的混合信号进行仿真分析,信号的表达式为

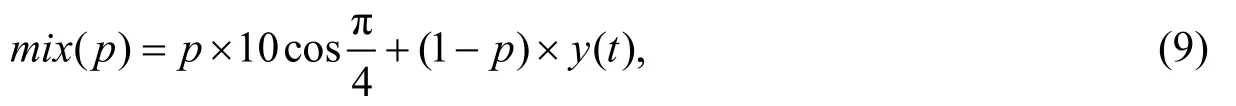
式中:p表示权值,y(t)表示随机的噪声信号。

设定试验采样时间为1 s,采样频率为2 000 Hz,分别计算p取值0.2与0.8时仿真信号mix(p)的MDE与RCMDE熵值,其中仿真信号对应的时域图为图2所示。

图2 混合信号mix(p)的时域波形图

计算得到的不同尺度因子下2种熵的熵值曲线如图3、4所示。

图3 MDE熵值曲线图

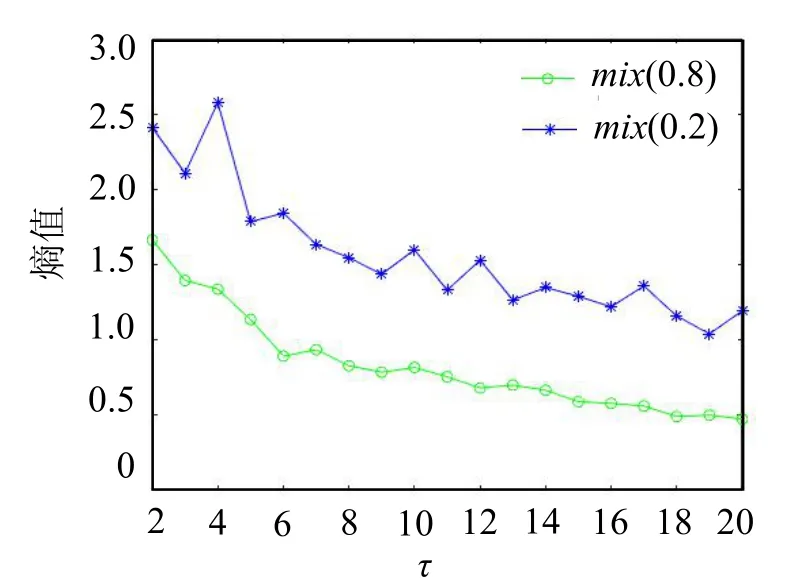
图4 RCMDE熵值曲线图

通过对图3和图4的比较与分析可知:MDE熵值算法对仿真信号进行特征提取时出现了大量的熵值曲线交叉现象,从而导致不同信号的可分性下降,引起特征提取结果的误差。由图4可知,2种不同仿真信号的RCMDE熵值曲线区分效果较为明显,且仿真情况与信号的实际情况相符,因此,RCMDE对于信号的特征提取有着一定可行性,并且RCMDE的熵值曲线整体情况较为平稳,这一现象也表明了精细复合多尺度散布熵算法的稳定性较好。通过上述对于MDE与RCMDE的对比分析,可以得出RCMDE具有更好的特征提取效果。

3 基于RCMDE的2D80-53.4型压缩机故障诊断

3.1 故障诊断实例

选用2D80-53.4型压缩机连杆的轴承振动数据进行实例验证,其电机转速为740 r/min,进气压力11.5 kgf/cm2,排气压力68 kgf/cm2,排气量为53.4 m3/min,轴功率为31 kW。根据2D80-53.4型压缩机的结构特点,选取位于2D80-53.4型压缩机中十字头滑道下端为传感器测点,来收集正常和磨损2种不同工况下轴承的振动数据,其中总共收集样本熵长度为1 024的160组样本进行实例研究。

3.2 振动信号分析

根据仿真分析可以得出压缩机轴承正常状态和轴承磨损状态下2种不同状态对应的时域图是不同的,由于压缩机振动信号复杂且非线性,轴承正常状态下的时域图表现为振动冲击性强,振动信号无规律且情况复杂;然而当轴承出现磨损时,轴承的轴瓦和内圈之间会出现运动间隙,从而产生巨大冲击,以致轴承磨损状态下的振动信号表现为有规律的冲击振动。

3.3 振动信号RCMDE熵值分析

采用RCMDE计算2种振动信号的熵值曲线如图5所示。预先设定参数,尺度因子τmax=20,相似容限γ为原始序列标准差的0.15倍,其结果如图6所示。然后分别采用MDE和CMDE 2种方法计算出轴承正常状态和磨损状态下的熵值曲线,如图7所示。

图5 2种信号的RCMDE熵值曲线

图6 2种信号的MDE熵值曲线

图7 2种信号的CMDE熵值曲线

由图5可知,本文方法求得的熵值曲线能够很好地区分开轴承正常状态和磨损状态2种状态。在随尺度因子τ变化,2种信号的熵值曲线变化趋势基本一致,熵值曲线虽存在微小波动,但不影响确定2种信号的复杂度情况,表明RCMDE方法在复杂信号分析方面具有较好的效果。当尺度因子τ=1时,RCMDE的值等于DE的熵值,其中轴承正常状态的熵值要小于磨损状态的熵值,而在多尺度上2种信号的熵值呈现出完全不同的熵值结果,并且熵值曲线变化趋于平稳。由图6、7的2个熵值曲线图可知,当尺度增加时,MDE和CMDE 2种熵值曲线的平稳性逐渐变差,并出现一些曲线交叉的现象。于是综合分析可以得出精细复合多尺度散布熵较另外2种熵值算法有着更好的特征提取效果。

通过收集的160组压缩机轴承振动数据对本文方法进行实例验证,其中,将随机抽取120组振动信号数据输入ELM智能分类算法中对分类模型进行训练,剩余40组数据作为测试集。利用上述的3种熵值算法对收集的160组轴承振动数据进行特征提取分析,并结合ELM智能分类算法对压缩机进行轴承故障诊断识别,得到测试样本的诊断识别结果如表1所示。由表1可知,本文方法的故障平均识别率为95%,且在轴承正常和磨损2种状态下的识别准确率比较其他方法仍为最高。

表1 不同熵值方法对应的2D80-53.4型压缩机故障诊断识别率 /%

4 结束语

针对2D80-53.4型压缩机轴承故障信号存在高耦合和非线性等特点,提出了基于RCMDE的2D80-53.4型压缩机轴承故障诊断的识别方法,并进行了验证。得出以下结论:

(1)利用仿真信号分析可知,精细复合多尺度散布熵相比于多尺度散布熵具有熵值曲线稳定且区分显著的优点;

(2)通过对2D80-53.4型压缩机的轴承振动信号进行实例验证可知,RCMDE的熵值曲线稳定性高,可分性良好,在故障特征分析上效果更加显著。