小波变换在混合系统时间序列离散事件检测中的应用

胡珍妮，代雪珍，周步芳

（西安交通工程学院，陕西西安 710300）

大多数技术的过程融合是由离散子系统和连续子系统的交互产生的。在状态空间的某些区域内，系统不断地演化，当达到这些区域的边界时，由于离散控制行为或物理现象[1-2]，连续动态不连续地发生变化，这使得连续状态变量的导数发生跳变。在过去的几年中，研究人员花费了大量的精力来开发这种混合系统的理论模型，用于离散控制器的仿真或验证[3-4]。另一方面，小波理论已成为在不同时间尺度上分析信号的强大框架[5]。通过信号在小波空间上的投影，得到了一种多分辨率表示方法，该方法提供了不同时间帧中不同频率的贡献信息。这一贡献说明，小波理论是分析混合系统产生时间序列的一个方便框架。

文中利用小波变换的系数来描述混合系统时间序列所获得的性能提升，并指出了用理论结果来检测实时序列中的离散事件时所遇到的问题。

1 小波理论与应用

小波变换的基本思想是将信号x分解成一组基本的构造块[6-7]，如下式所示：

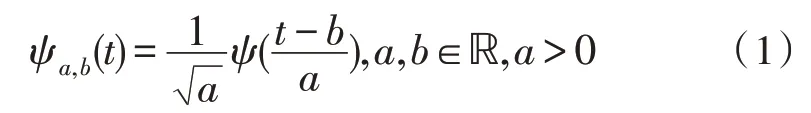
这些基本函数是从一个在时间和频率上局部化的母子波中通过缩放和平移操作得到的。

因此，连续小波变换不仅指示信号中包含的频率，而且表明频率内容是如何随时间变化的[8]。因为当尺度参数a减小时，小波在越来越短的时间间隔内被局部放大，所以对于更高的频率，时间局部化变得更精细:

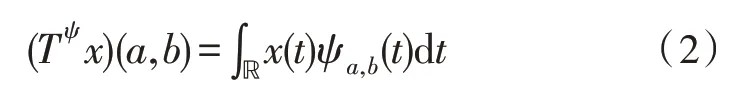
小波的缩放和平移如图1 所示，对于较小的a值，小波在较短的时间间隔内局部化，而频率内容被放大并移到较高的频率。在实践中，尺度参数通常仅限于离散值a=2j,j∈ℤ。

图1 小波的缩放和平移

如果信号由离散时间实例x={x(k)}k∈ℤ的值给出，假设采样间隔Ts=1，则在每个离散尺度上的转换参数b被限制为离散采样时间b=k。在这种情况下,平移步长保持不变，而ψj,k的时间支持度随着离散尺度j的增大而增大。为了避免基函数的冗余和产生由少数系数构成的稀疏表示，通常选择b随着每个离散尺度的增大而增大[9-10]，b=l∙2j,l∈ℤ(矢离散化)。x在基函数的离散集合上的投影如下：

由此得到了平移不变小波变换的系数(Tψx)(2j,k)。对于分析小波的某些选择，可以通过滤波操作进行有效计算：从离散样本{x(k)}k=1,...,n开始，作为尺度j=0处信号的最佳近似，尺度j=1 系数(Tψx)(2j,k)的计算需要使用O(n∙logn)操作。

信号可通过其连续小波变换重构：

由于最细的尺度对应于较高的频率分量，因此在重构时忽略这些尺度可以获得原始信号的粗略近似。一个重要的特征是分析小波消失矩的个数，其中第k个矩被定义为∫ℝtkψ(t)dt，这个特征表征了是否可以通过这种方式获得接近原始信号的近似值(即具有较小的均方误差)。使用具有N个消失矩(即∫ℝtkψ(t)dt=0,0 ≤k≤N-1)的小波可以过滤多项式Pm(t)，直到m≤N-1，即小波变换(TψPm)(a,b)取零值。

此估计仅对信号平滑的区域有效，即至少N次连续可微的区域。否则，信号或其导数的奇异性会限制多项式逼近的阶数，从而导致小波变换的幅值会局部减小，这就是小波变换在尺度上的演化可以用来表征信号局部规律性的原因。此外，高频分量对系数减小的影响是局部的，这使得具有稀疏奇异性的信号能够进行稀疏表示。

1.1 小波阈值收缩

如果对噪声信号xN={xN(k)=x(k)+ε(k)}k=1…n(其中，假设ε(k)独立地分布为N(0,σ2))进行变换，则噪声对所有系数(TψxN)(2j,k)的影响是类似的。相反，如果原始信号x只有稀疏奇异点，则可以将其压缩为其小波变换的几个系数。通过将大多数(TψxN)(2j,k)设置为零，部分噪声就可以被消除。

通常的去噪方法是忽略傅里叶系数，即切断了大部分系数受噪声支配的最高频带[11-12]。然而，小波系数的多分辨率表示使得能够在每个频带内选择对信号有显著贡献的系数。仅使用这些信号进行重构，既能降低噪声，又能保留局部高频现象。有效系数的选取通常采用阈值化的方法,即只选取超过阈值λ的系数进行信号重构：

式中，n是待去噪信号的长度。如果使用正交小波，则可以通过变换的最小尺度j=1 的系数(TψxN)(2j,k)的方差来估计叠加噪声的方差σ2。

1.2 奇异点的检测和表征

文献[13]中利用小波变换绝对值的演化与被分析信号的局部规律性之间的关系来检测和表征奇异点，该文献表明，t∗处的奇异点在小波变换绝对值中产生一系列极大值向t∗收敛，标度a→0。因此，可以通过跟踪从粗尺度到细尺度的最大值来定位奇异点。同样，只要分析小波至少有N+1 的消失矩，就可以检测出N阶导数的奇异性。通过信号与平滑函数θ的卷积，信号中的不连续性被转换成拐点，由此可以在平滑信号的一阶导数的绝对值中检测出最大值,如图2 所示。由于具有N个消失矩的小波是平滑函数的N阶导数(见图3)，因此固定尺度上的连续小波变换可以解释为平滑信号的N阶导数。因此，阶数小于N的导数的跳变表现为极大值。此外，通过考虑不同尺度，即不同的平滑度，可以根据小波变换幅度沿相应极大值的演化来估计t∗处的规律性。

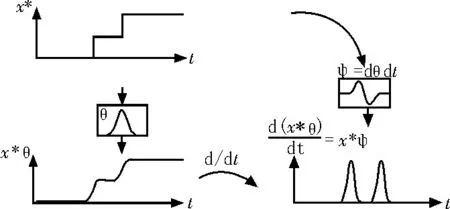
图2 计算机视觉中的边缘检测

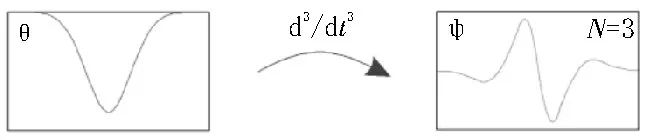
图3 样条小波的平滑函数及其三阶导数

2 离散事件的小波检测

结合混合系统的特点和小波变换，可以通过以下方式利用混合系统的小波系数表示时间序列[14]：在系统连续演化的区域，小波变换的振幅在尺度上迅速减小，其减小仅取决于分析小波ψ的消失矩数N。在该文中，时间序列可以用粗尺度上的系数来表征。然而，离散事件将局部正则性限制在导数的m阶，其中离散事件导致在这个阶上出现了不连续。根据文献[13]的结果，如果分析的小波具有N>m个消失矩，则这些变换会在小波变换的绝对值中产生一系列的极大值，这些极大值以减小的尺度a→0 向变换点t∗收敛。因此，离散事件可以通过从粗到细的尺度跟踪最大值来定位。此外，小波变换振幅在尺度上的减小可以用来表征模态变化(即发生跳变的导数)，并将离散事件引起的跳变与拐点区分开来。

在实际应用中，由于计算费用的原因，检测过程的第一步只计算离散尺度上的系数a=2j。如前所述，所考虑的尺度范围受到信号到j∈ℕ 的分辨率的限制。根据平移不变小波变换的系数(TψxN)(2j,k)的结果表示，执行以下步骤：

1）通过评估相邻极值之间的距离，确定系数绝对值中最大值的线(在后面的图中表示为极值线)。

2）通过相邻离散尺度之间的减少来表征最大值线，如下式所示：

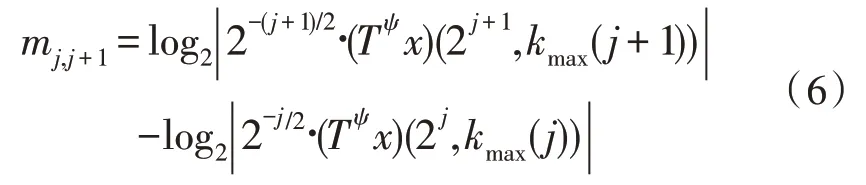
其中，kmax(j)表示离散尺度j上绝对值中最大值的位置。

3）同一事件会引起最大值线的融合，即值相同且彼此接近，切换点k∗由最细尺度j=1 上相应极大值的位置kmax(j)的平均值确定。

图4 所示为使用3 个消失矩样条的小波进行分解时的时间序列系数。在这种表示中，由于耦合或解耦(k∗=848 和k∗=994)以及流入流量的切换(k∗=939)而产生的离散事件，显示为系数绝对值的最大值。考虑到最细尺度j=1 的值，显然，由于离散事件，二阶导数(α=2)中的连续性只强制执行每个极值对中的第一个。相反，剩余极小值的减少表明，局部正则性受到小波消失矩数(=3)的限制。这些极值对应于时间序列二阶导数中的拐点，这是由于在相反方向跳跃之后指数的增加，如图5 所示。考虑到系数振幅沿相邻最大值线的演化，即使极值彼此接近，也可以区分两个特征，这意味着它们的距离保持在小波分析影响内的每个离散尺度上。

图4 离散事件的时间序列系数转化为绝对值的极大值

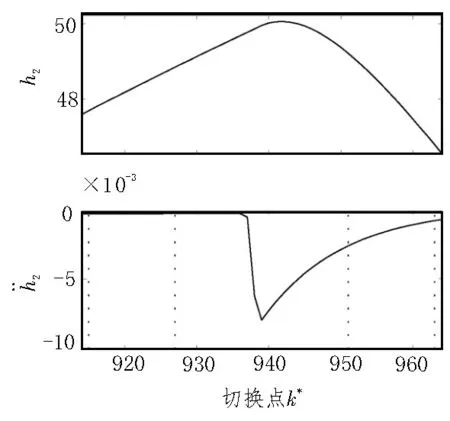
图5 k∗=938附近的时间序列及其二阶导数

因此，当考虑到最细的两个尺寸时，这3个离散事件可以被适当地局部化和表征。此外，通过评估沿剩余最大值线的系数振幅的演变，可以排除在考虑的时间间隔内进一步发生阶数小于m=3 的模态变化。

随着标度j的增加，mj,j+1的值与α=2(离散事件产生的最大值)或α≥3(对应于连续演化的最大值)的差异越来越大。对于某些离散尺度j，即使对于对应于拐点的极值，mj,j+1的舍入值也表示二阶导数的跃迁。而且，如果只考虑第四和第五个尺度，则这两种现象在k∗=938 附近不能再区分。相反，将2的跃变和指数演化的组合“解释”为狄拉克冲量，它被转换成两条最大值线，其中沿每一条极大值线的衰减给出了=1 局部规律性(h2一阶导数不连续性)。在这种情况下，在检测程序的第三步中，将切换点k∗计算为两个极值位置kmax的最佳比例的平均值。

考虑到此处评估的系数对应于时间序列二阶导数的一个越来越平滑的导数，如果2在k∗的两侧保持不变，即h2是m≤2 次的多项式，则系数的减小幅度在所有尺度上保持不变。由于多项式是通过小波分析进行滤波的，因此周围的信号在任何尺度上都不会影响相应极值的演化。然而，如图5 所示，随着离散尺度的增大，平滑跳跃的最大斜率减小得更快。因此，除标度因子外，表征最大斜率系数的最大振幅在离散尺度上的增长速度并不像考虑到k∗处的局部规律性所期望的那样快。

基于这些规则，对于文中考虑的所有离散尺度，可以正确估计k∗=938 的局部规律性。相反，对于对应于转换点的局部规律性的评估，仅限于Jmin=2。除了每个转换点附近信号的影响外，在标度j=5 时，k∗=938 和k∗=994 处的转换相互影响，使得m4,5的一个值变为负值。考虑到小波分析对每个尺度j的支持，可以很容易地评估并排除这些尺度的影响。由于小波在边缘处的振幅很小，因此使用了一个缩小的区间，该区间对应于至少90%总和的积分绝对值。通过考虑相邻切换点之间的时间差，可以避免对拐点最大值的错误检测。

3 存在噪声的情况下检测离散事件的程序

随着尺度的上升，转换点附近的信号对k∗的规律性的影响越来越大，这就是使用基于系数最大值的检测与小波收缩过程相结合的原因。图6 所示为检测离散事件的程序在Matlab 中的实现。

图6 检测和去噪的结合

首先使用平移不变小波收缩方法对信号XN进行去噪。在该步骤中，选择超过通用阈值的系数(被假定不受噪声控制)用于重构信号。由于离散事件在绝对值上被转化为极大值，它们更有可能超过阈值，因此在重建中被考虑。相比之下，在系统不断演化的区域，所得到的时间序列是平滑的，因此在没有高频成分的情况下，系数下降很快，在这里可以在很大程度上消除噪声。

第二步，对去噪后的时间序列进行再次变换，随后评估所得的最大值，以定位和表征离散事件[15-16]。此外，通过考虑离散事件在尺度上的演化，可以将离散事件对应的极大值与剩余噪声对应的极大值区分开来。

通过将这两个过程结合起来，可以利用平移不变小波变换的粗尺度系数的冗余来重建每个离散事件在至少一个较细尺度上的最大值，该尺度由噪声控制。

以弱噪声(信噪比为200)叠加的时间序列为例，说明组合过程。图7 比较了模拟时间序列与噪声信号及其在第二个离散事件附近的二阶导数。在图7中，虽然时间序列本身只有细微的差别，但2的二阶导数完全被噪声所控制，无法检测到k∗=938 处的跳变。

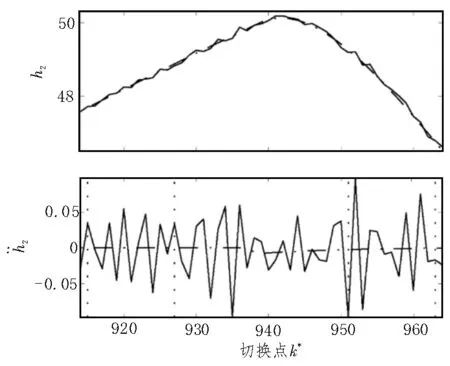
图7 有噪声时的时间序列及其二阶导数

图8 比较了从选定系数重建的时间序列与无噪声时间序列。对于第二次分解，使用3 个消失矩样条小波。可以看出，提出的组合允许利用粗尺度系数的冗余部分重构细尺度的最大值。此外，与小振幅(伪影)跳变相对应的附加极值随尺度的上升而减小，因此在检测中不考虑。如果在第二步中使用具有更多消失矩的小波(N>3)，则信号平滑部分的系数衰减得更快，因此，可以更精确地估计局部规律性。然而，由于具有更多消失矩的小波具有更大的支持度，因此，系数幅值的演化受离转换点较远的系统动力学的影响。

图8 时间序列的系数

在去噪过程中，使用具有较少消失矩的小波是有用的，这是因为离散事件被“转换”为具有较大幅度的较少系数，相应的系数更有可能超过阈值。通过这种方式，可以实现更大的局部细化，从而减小离散事件的失真。

4 结论

文中提出了在混合系统时间序列的第m阶导数中检测离散事件的方法，应用的是计算机视觉中的边缘检测技术，包括平滑和计算至少m+1 阶导数的组合。在这种背景下，小波理论已被证明是一个合适的方法。由于在不同的平滑级别上的同时视图，切换不仅可以通过相应的极大值位置来定位，而且还可以通过其振幅在尺度上的演化来表征。然而，在噪声存在的情况下，检测导数的跳变需要对粗尺度进行评估。文中探讨了当系数振幅的评估仅限于较粗尺度时发生的影响，然后将基于系数最大值的检测与基于小波的去噪过程相结合。后者允许在转换点附近进行局部细化，从而减少噪声，并使离散事件的失真最小。通过这两种方法的结合，可以对之前被噪声控制的最大值部分进行重构，从而扩大了可评估的尺度范围。