栅格网络空间下基于加权核密度估计法的公交场站供需分布模型
谭英嘉, 况 雪
(深圳市综合交通与市政工程设计研究总院有限公司, 广东 深圳 518000)
随着国内城市化步伐加快,逐渐形成密集和紧凑的城市布局特征。同时城市居民出行需求日益提升,导致了交通拥堵问题日益凸显恶化。优先发展城市公共交通,可有效缓解交通拥堵,提高人们的出行品质,促进城市交通朝着可持续方向发展。公交场站作为常规公交的重要基础设施,保障了常规公交正常运营。然而目前大部分公交场站的供应水平未与公交需求匹配,导致中国大部分城市在线网优化组织、车辆运营调度中面临较大场站缺口,公交场站建设滞后成为中国城市公共交通发展的瓶颈之一。为此对公交场站现状供需进行准确分析就显得尤为重要。
国内外学者对公交场站规划、建设、开发均进行了一定研究,但对公交场站的供需分布、供需匹配的研究较为缺乏。Chen等[1]研究了公交站点容量与停车需求之间的关系,提出将公交车辆到发站点视为生死存亡过程,从供需协调角度建立了多停车位的公交站点停车能力可靠性模型。Gu等[2]认为在进行公交站点选址时应综合考虑相邻车站的客流特征及其他车站位置。Di等[3]为解决公交供需不匹配等问题,利用公交GPS、IC卡等数据,基于4个时间维度,利用各公交站点的日均登降量、线路日均客运量等数据来呈现不同层次的常规公交需求。Zhou等[4]建立了一种新的公交场站编码方法及其供需能力之间的匹配模型,以找到供给与需求之间的平衡点,识别场站供需情况,确定需要优化的场站。对于场站需求规模的确定,Javid[5]融合公交运力、职员数量、等候乘客数量等因素分析了公交场站规模,确定了设置场站合理规模的范围。翁勇[6]、王满[7]基于公交客流预测结果,构建了综合常规公交出行量与公交配车数的模型,在确定公交配车规模的基础上预测了场站需求数量。
关于公交场站需求分布的研究方法,核密度函数估计法是一种非参数密度估计方法,对数据分布不进行任何先验假定,通过数据样本来研究数据的分布特征[8]。在空间分析方面,核密度法常用于研究城市点要素空间分布模式,其结果表现出距离核心越近的区域所受中心辐射值越大的特征,符合城市设施服务对周边位置影响的扩散特点。禹文豪等[9]建立了分析热点区域特征的核密度估计模型,并考虑弧段不规则排列的约束及网络计算的效率问题,提出了一种基于一维栅格参考系及形态运算的网络核密度计算方法,提高了算法效率。陈金林[10]利用修正后的核密度估计法对城市路网事故黑点进行了鉴别研究,并基于ArcGIS软件实现了基于核密度估计法的城市路网事故黑点鉴别结果可视化需求。郑伟等[11]针对高速公路交通流速度分布特征,选取高斯核函数进行核密度估计分布计算,对核密度估计分布进行拟合检验,认为核密度估计法能较好地拟合交通流速度的概率分布。Srikanth等[12]基于核密度估计和热点分析方法对交通事故热点进行了识别和排序。
现阶段对于公交场站的供需匹配、供需分布的研究较为薄弱,大部分研究对公交场站需求预测进行了建模分析,但偏理论性,很难真正有效地辅助实际决策过程,模型方法实用性、可操作性差。因此本文针对首末站、停车场、保养场等除中途站外的公交场站,基于地理栅格网络,采用加权核密度估计法构建公交场站供需分布模型,对地理栅格网络空间中的场站需求、供给规模以及供需栅格层数据叠合后的供需比数据进行了计算,最后以栅格网络形式可视化场站供需在地理空间上的分布,清晰呈现其分布特征、分布模式,为寻求场站缺口,平衡场站供需提供数据支持、可视化支撑。
1 公交场站相关理论概述
1.1 公交场站范围界定
公交场站是指城市公共汽电车场站,在城市公共汽电车系统中为乘客提供上下车、候车、换乘等服务,并提供车辆停放、运行调度、管理维护等活动的场所及空间[13]。根据《城市道路公共交通站、场、厂工程设计规范CJJ/T 15—2011》[14],可将公交场站划分为车站和车场两类。其中,中途站和枢纽站为车站,而首末站、保养场、修理厂和停车场均为车场[15]。本文主要是对具有停放功能的车场进行供需分布研究。
1.2 不同类型的公交场站用地标准
根据《城市道路公共交通站、场、厂工程设计规范CJJ/T 15—2011》[14]建议的每标台公交车辆的停车需求面积,不同类型的公交场站对应的车辆占地面积标准不同,见表1。
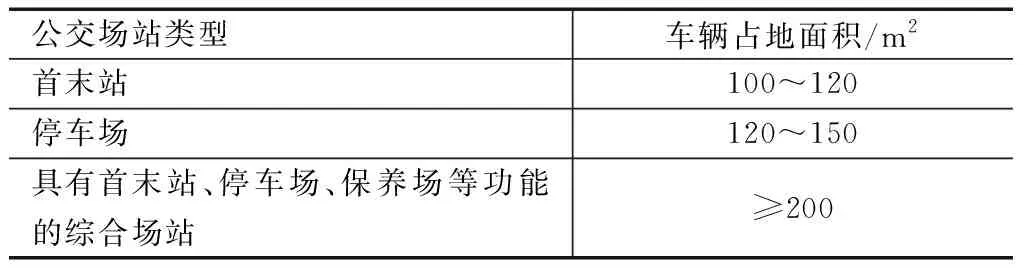
表1 不同类型公交场站对应车辆占地面积标准
1.3 公交场站存在的主要问题
1)公交场站供应未能满足公交车辆需求。公交场站是保障公交车辆正常运行的基础设施,随着居民出行需求日益增长,城市大力发展公共交通,公交车辆规模也随之发展扩大,公交车辆对于停车、修理、保养的需求也越来越多,而城市用地约束紧,公交场站建设进度通常滞后于规划,建设速度跟不上公交车辆增长速度[13],导致公交场站规模越来越无法满足公交车辆需求。
2)公交场站布局与公交车辆实际需求不匹配。大部分公交场站进行选址时,未结合城市内公交车辆的停放等需求对场站的分布进行布局规划,导致公交场站供需在时空上发生错位[16]。公交场站的时空错位会导致公交车绕行距离增加,降低了公交场站的服务水平,同时加剧城市交通拥堵情况。在错位较严重时,区域间的公交场站供需无法协调,导致某些区域的公交车辆无场站可用,而另一些区域场站空间利用不充分,造成资源浪费。
3)公交场站类型比例失衡导致公交线路布局不合理。公交场站一般可根据用地性质分为固定场站、企业自有场站和租赁场站3类。部分城市的租赁场站比例远高于固定场站,因此租赁场站的不稳定性[13]可能会造成城市内的公交线路布局不够合理,影响公共交通持续发展。
因此,研究公交场站,优化公交场站布局,增加、调整部分场站供给显得尤为必要。
2 核密度估计
2.1 核密度估计算法
公交场站受服务范围和场站间叠加效果等因素的影响,其供需的分布特征呈现非线性的特点,无法用线性方程等来进行分析,即没有先验知识确定公交场站供需数据的概率密度函数,需要使用非参数估计的方法进行分布分析。Rosenblatt在1955年提出了核密度估计,即在一种样本估计未知分布情况下概率密度函数的非参数估计[11]。设X1,X2,…,Xn为单位变量X的独立同分布样本,则X服从的概率密度函数的核密度估计为
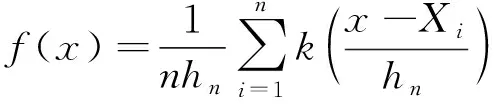
(1)
2.2 核函数及窗宽的选择
2.2.1 核函数对比
现比较7种不同类型的核函数,见表2,不同核函数的权重变化规律不同,会对核密度估计过程的加权平均结果造成影响。文献[17]比较了表2中7种不同核函数估计的精确度,其结果表明相较其他核函数,四次核函数具有更好的估计效果,因此本文选择四次核函数来进行核密度估计。

表2 核函数表达式
2.2.2 计算最适窗宽
窗宽的选择对核密度估计影响很大,决定了核密度估计函数曲线的光滑程度及数据包含信息量[11]。窗宽主要取决于设施点的影响范围及设施点间的距离两个因素[18],选择合适的窗宽能准确评估样本数据的聚类特征。在选择的窗宽越小的条件下,核密度估计将概率密度分配在样本点周边,概率密度分布的局部差异更突出,能反映更多数据包含的细节信息,但核密度估计曲线会随窗宽变小而变得更粗糙,核密度估计函数曲线不平滑会导致最终的估计结果与实际情况不符。当窗宽值越大,概率密度分配范围越广,此时的核密度估计曲线更为平滑,但当研究范围扩大时,重要信息就易被忽略。故需要选取合适的窗宽来进行核密度估计,在保留样本数据分布特征的基础上尽可能减少重要信息的损失[11]。
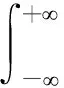
在概率论与数理统计中,通常采用概率密度函数与真实的概率密度函数之间的均方积分误差(MISE)来确定窗宽[17]。
AMISE(h)+o{(n-1h-1)+h4}
(2)

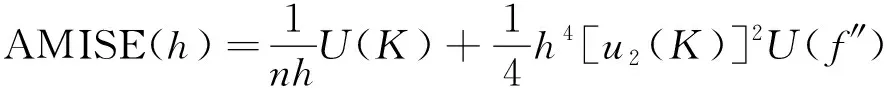
(3)

由式(3)可知,AMISE(h)式关于窗宽h的表达式,则最优窗宽hp能使表达式(3)达到最小值,因此采用求导法对AMISE(h)进行求导,来计算hp。
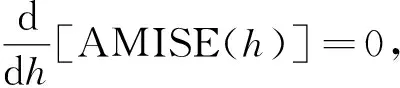
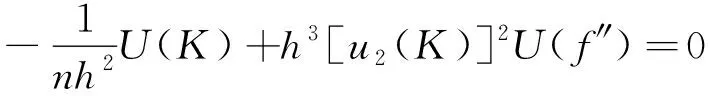
(4)
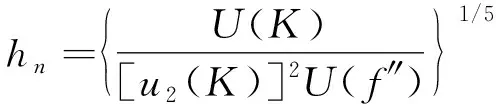
(5)
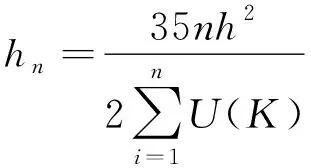
(6)

同时,当样本群为服务或者商业设施等类型时,由于此类设施的POI性质会影响核密度估计时的窗宽值,可根据此类设施的影响范围及设施点间的距离等主要影响因素确定其窗宽值。设所有样本点的影响范围为l,样本间的距离为dij,当dij∈(m,n)时,可取hn=l。
3 基于加权核密度估计的公交场站供需分布模型
为缩减计算量并提高算法效率,同时对核密度估计结果进行可视化,本文在构建供需分布模型时结合了栅格数据模型,将城市地理空间划分为有限个空间位置由像元的行列号表示的网格单元,通过模型算法分配给每个栅格相应的场站供需规模数据,再利用栅格存储的数据进行可视化处理。因此在构建供需分布模型前先将公交场站分布的地理空间划分为致密的栅格单元,建立栅格数据模型。
接下来在构建供需分布模型时,首先是对公交场站需求进行分析,公交场站主要是满足公交车辆停放等需求,因此对公交场站需求规模进行确定的主要内容是预测区域的公交配车规模。研究过程为通过获取公交出行量,对公交配车量进行估算,最后计算公交车辆对于公交场站的面积需求。
为准确表示不同区域的公交出行量,本文采用公交站点日均上客量来进行分析。由于公交站点吸引客流按距离递减,因此利用核密度估计法对站点上客量在一定范围内进行分配,可获得站点周边的栅格单元中公交出行量分布情况。然后通过公交车辆单车日均客运量将分配至每一栅格单元的公交出行量转换为日均公交配车数,最后根据规定的公交车辆占地面积测算栅格网络中公交场站需求面积。
研究文献表明,地区人口及就业率是影响公交出行量的主要因素,区域停车场数量也是影响因素之一,商业等行业对交通出行量的影响也比较明显[19]。考虑到公交车辆是城市公共交通的重要载体,因此在进行公交出行量分配时,需引入相关参数的权重对核密度估计进行修正[20]。总结较为重要的影响因素,得到表3所示的人口经济、土地利用、交通出行3类公交客流影响因素。

表3 公交出行量影响因素
考虑相关数据获取难易度,指标计算的复杂程度以及指标的重要性,本文选取表2中的人口密度、路网密度、公交可达性3个指标的权重来修正核密度估计结果。
接下来对区域的公交场站需求进行建模分析,设栅格序号为i=1,2,…,m,公交站点序号为j=1,2,…,n,则第i个栅格分配到公交站点j的公交出行量可表示为

(7)
f(w)=wpiwniwabi
(8)
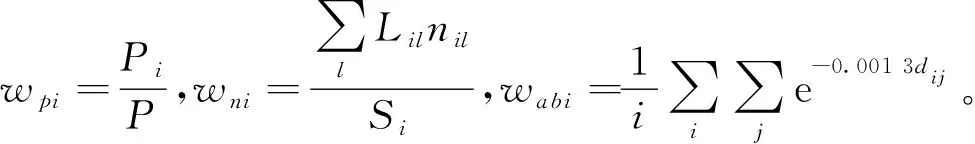
得到栅格i的公交场站需求面积Ri为
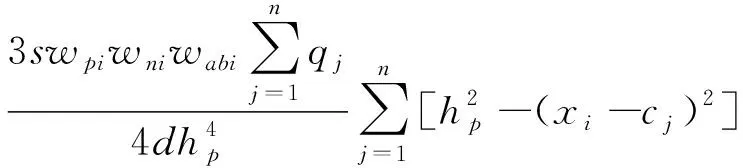
(9)
式中:qij为公交站点j分配至栅格i出行量;qj为公交站点j的上客量,也被称为此处的公交出行量;hp为公交站点分布的最适窗宽;xi为栅格i在网络空间中的位置标记点;cj为站点j在网络空间中的位置标记点;f(w)为公交站点出行量分布的权重函数;wpi为栅格i占人口密度指标的权重;wni为栅格i占路网密度指标的权重;wabi为栅格i占公交可达性指标的权重;Pi为栅格i包含人口数;P为计算区域总人口数;Lil为栅格i中路段l的长度;nil为栅格i中路段l的车道数;dij为栅格i到站点j的距离;Qi为栅格i的公交配车数;s为每标台公交车辆规定的占地面积;d为常规公交的单车日均客运量;Ri为栅格i的公交场站需求面积。
对公交场站供给分布进行分析,利用核密度估计法对现状的公交供给规模在一定范围内进行分配,分配时考虑影响场站分布因素对核密度估计函数进行修正。总结文献及相关理论,认为公交场站供应分布与公交场站需求分布、路网密度两个因素相关性最高,因此在建立模型时兼顾这两个参数的影响。
设场站序号为k=1,2,…,N,则第i个栅格分配到场站k的供给面积表示为
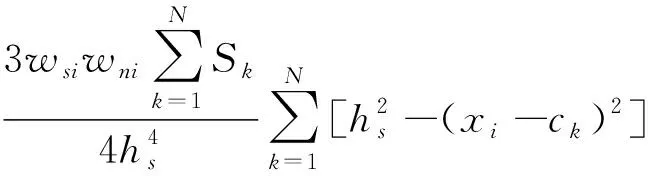
(10)
式中:xi为栅格i在网络空间中的位置标记点;ck为场站k在网络空间中的位置标记点;hs为公交场站分布的最适窗宽;y(w)为公交场站供给规模分布的权重函数;wsi为栅格i占人口密度指标的权重。
最后对公交场站供需情况进行综合分析,将前文建立的公交场站需求及供应分布模型进行整合,可得到公交场站的供需分布模型。即通过栅格数据叠加分析方法对供需两个栅格图层在空间统一位置上的栅格像元值进行运算,得到公交场站供需分布的栅格数据层。将供需层数据叠加后得到的供需比定义为供需指数。
供需指数δ的计算公式为

(11)
根据计算得到的供需指数,可对每一栅格单元的公交场站供需情况进行评价,为决策者找准供需缺口并进行优化提供可靠依据,现将供需指数划分为3种类型:δi>1,栅格i的现状场站规模供给不足;δi=1,栅格i的场站面积供需规模平衡;δi<1,栅格i的现状场站供给规模充足。
4 应用案例
选取深圳市作为研究区域,通过收集并处理深圳市相关数据,构建供需分布模型分析深圳市内的公交场站供需分布特征,以验证本文构建模型的适用性、有效性。
首先通过获取求解模型相关基础数据,利用交通规划仿真软件TransCAD6.0构建基础数据库,并对数据进行可视化展示,公交站点上客量如图1所示,公交场站现状面积如图2所示。通过整理数据可得到深圳市现共有公交场站464座,总面积为297.5 hm2。
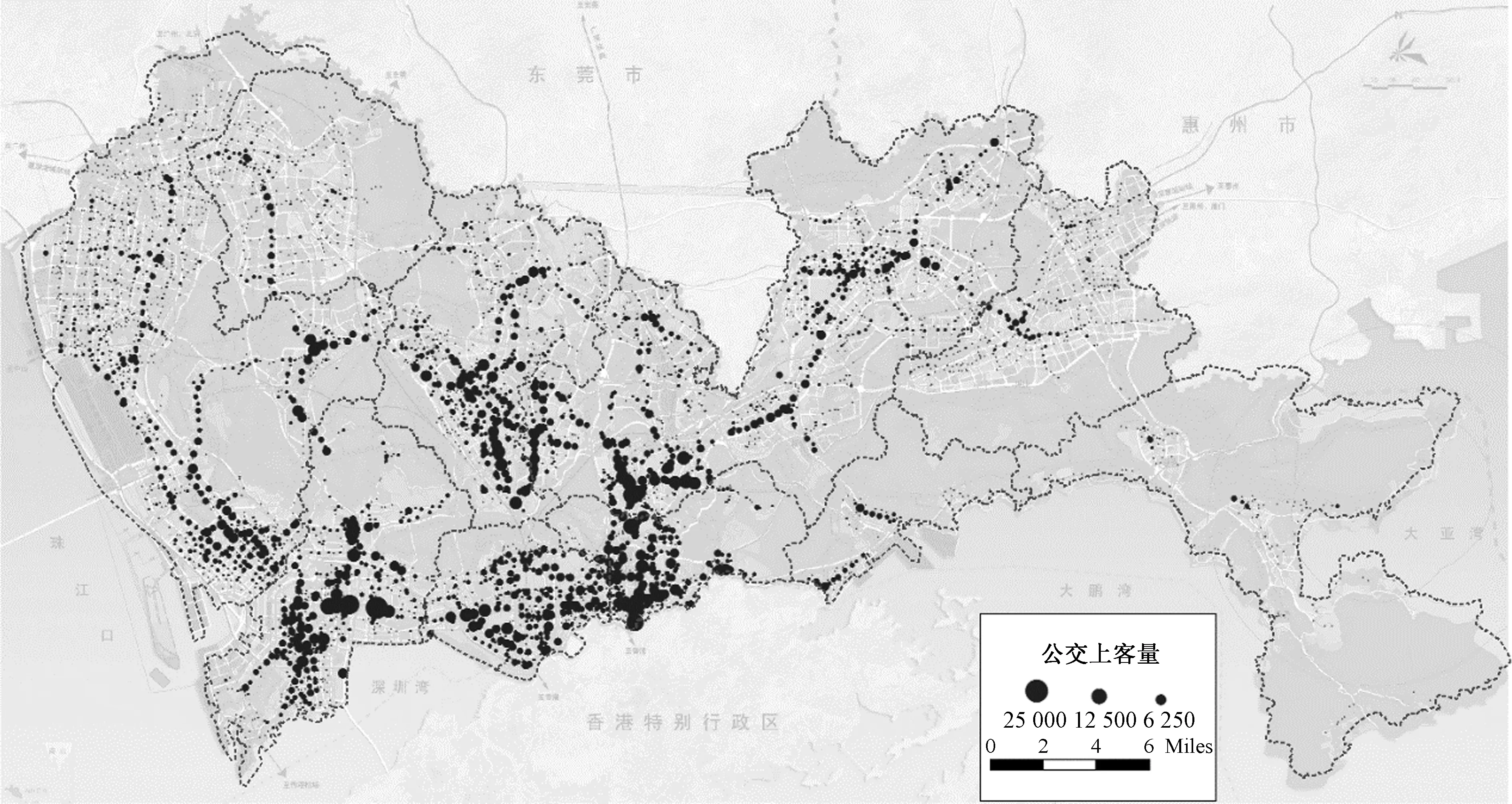
图1 公交站点上客量饼图

图2 公交场站面积饼图
为尽可能精确地估计栅格的场站供需规模,在模型参数设定过程中以大量实际数据为基础,以行业标准和规范为依据,以上一节对模型参数的定义为标准,进行参数标定,具体情况见表4。

表4 模型参数标定
最终将参数代入式(11)后得到

(12)
使用TransCAD6.0对深圳市地理空间进行栅格化,将像元划分为分辨率500 m×500 m的网格来进行分布情况的呈现,结合TransCAD和Arcgis两个软件在栅格空间中对模型进行求解,并利用echarts及高德地图的amap-js等工具辅助可视化公交场站供需分布数据,得到场站供需在栅格网络空间的分布结果如图3所示。为更清晰地从街道单元获取公交场站供需分布情况,将深圳市公交场站供需比的栅格数据映射到街道中,得到图4的街道场站供需情况,图中信息表明深圳市既有场站空间分布与实际需求未匹配。罗湖、福田、南山、龙岗、宝安、龙华6个辖区中仍有街道存在场站供需缺口。罗湖区东门街道、南湖街道的供需指数均超过20;罗湖区桂园街道、笋岗街道的场站供需指数超过10;福田区华强北、园岭、福保等街道的供需指数接近10,以上街道的场站供给规模远不能满足公交车辆停放、保养、修理的需求,因此在深圳市所有辖区中,罗湖和福田两区的供需缺口相对更大。
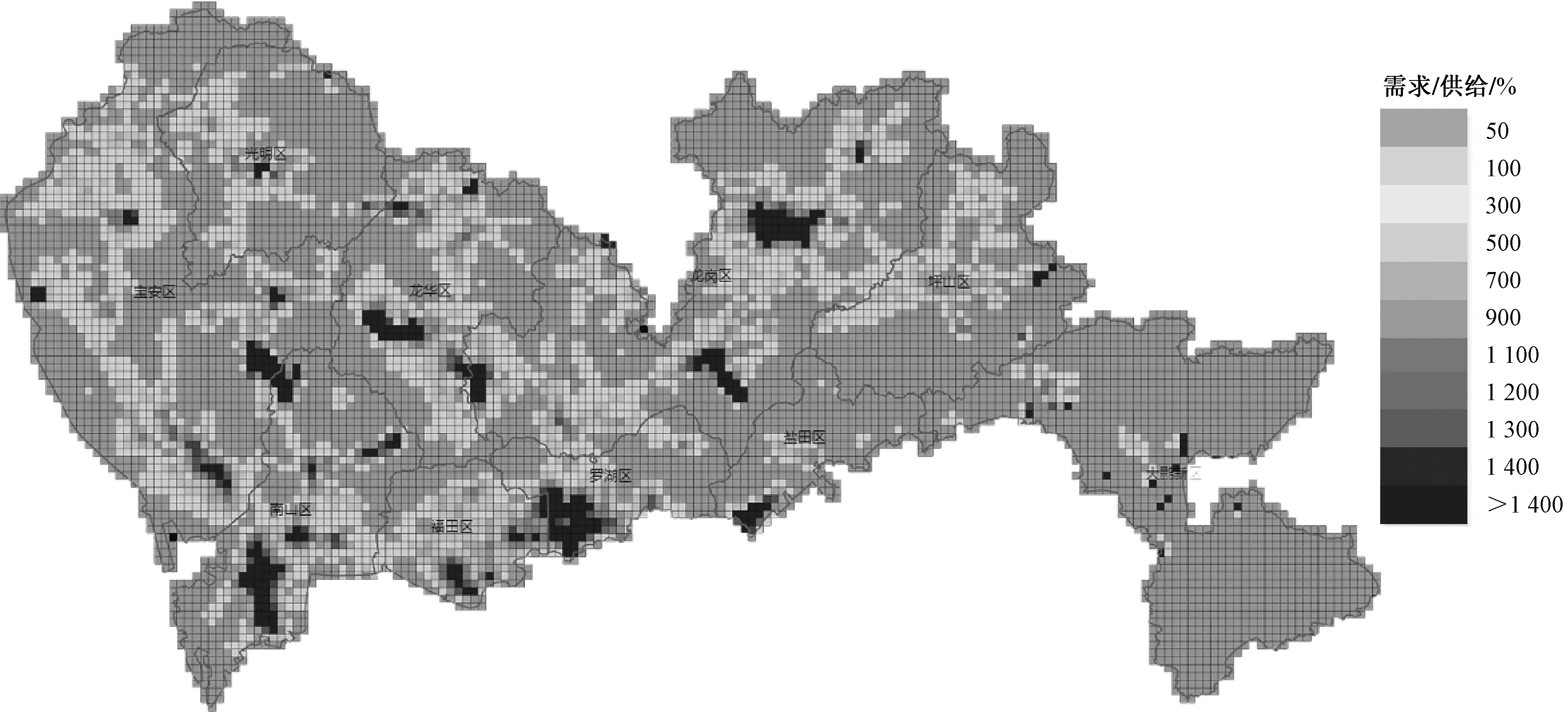
图3 深圳市现状公交场站供需分布情况
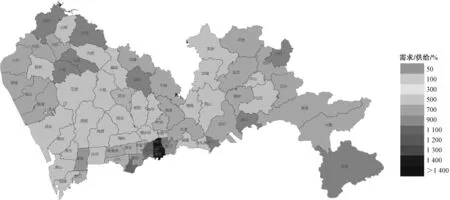
图4 深圳市各街道现状公交场站供需情况
5 结论
1)将地理空间划分为规则单元(像元),建立了栅格数据模型对基础数据进行存储、计算及展示,在此基础上,选择核密度估计算法对站点上客量以及场站面积在空间中的分布进行概率密度估计,并分别建立了需求和供应分布模型,最后基于多层栅格数据叠合分析方法构建了解析场站供需分布特征的栅格估计模型。
2)构建的供需分布模型利用改进的加权核密度法可以更准确地计算公交场站影响范围内栅格单元的供需规模,将场站供需分布评价细化到城市的每个栅格单元模拟场站分布情况,通过定量分析区域场站供需分布模式,可更科学合理、简捷快速地确定场站供需缺口的位置及规模,为优化决策提供依据。
3)选取深圳市为研究区域,以深圳市实际数据为支撑,基于TransCAD、Arcgis等软件,利用供需分布模型对深圳市的公交场站供需分布特征进行定量分析、可视化展示,清晰地展现了这座城市公交场站覆盖区域和分配情况,可得到罗湖区及福田区场站供应缺口较大的结论,验证了模型的有效性及适用性。
4)为准确有效地估计场站供需分布,虽对核密度估计法进行了改进,增加了多项权重进行修正,但忽略了实际的场站供需应沿着街道路径分布,因此为更加准确、客观地反映城市公交场站布局,需进一步提高模型适用性,在下一步研究中考虑街道网络约束,研究基于网络路径距离的核密度法来确定公交场站的区域密度,分析、呈现公交场站沿交通网络布局的空间特征。

