基于CEEMDAN和FRFT的多分量LFM信号参数估计

陈 宝，石耀坤，何国华

(桂林长海发展有限责任公司，广西 桂林 541001)

0 引 言

线性调频(LFM)信号是一种常用的脉冲压缩信号和典型的非平稳信号，具有大时宽带宽积等优点，可以获得较远的探测距离和较高的距离分辨率，在雷达、通信等领域应用非常广泛。因此LFM信号的检测和参数估计一直是非常重要的研究课题。但在实际应用过程中，对LFM信号的检测和参数估计容易受到各种噪声和其它信号的干扰，如何抑制这些干扰非常重要。本文将自适应噪声完备集合经验模态分解(CEEMDAN)和分数阶傅里叶变换(FRFT)结合，提出了一种新的多分量LFM信号参数估计方法。

1998年诺顿·黄等人提出了一种非平稳非线性信号的信号分解方法——经验模态分解方法(EMD)，它可以将信号分解成按频率由高到低排列的固有模态函数(IMF)。2011年，Torres等人在EMD基础之上，提出了自适应噪声完备集合经验模态分解(CEEMDAN)，其通过计算特定余量来获取各个模态分量，分解过程具有完备性，重构误差几乎为零，有效地解决了模态混叠问题，应用领域非常广泛。

截止到目前，针对LFM信号参数估计已经出现了很多数字信号处理算法，经典的傅里叶变换(FT)仅适用于平稳信号。针对这个问题，近年来，研究人员提出和发展了一系列新的分析方法，例如短时傅里叶变换(STFT),Wigner-Ville分布(WVD)，FRFT等，其中STFT受信噪比影响大，同时无法兼顾时间和频率的分辨率，WVD处理多分量信号时容易受到交叉项影响，导致分析结果失真。分数阶傅里叶变换(FRFT)作为一种较新的时频变换方法，Namias首先从数学角度提出了定义，Almeida分析了它和WVD变换的关系，并解释成时频平面的旋转算子，同时FRFT对LFM信号具有很好的聚集性，受噪声影响小。

本文在上述研究基础上，提出了一种基于CEEMDAN和FRFT的参数估计方法，其基本思想是使用CEEMDAN分解信号，获取多个IMF分量，根据每个IMF分量的傅里叶频谱方差，选择有用的IMF分量完成信号重构，并基于分离思想和拟Newton法对重构信号做FRFT处理，获取信号参数，仿真结果验证了该方法的可靠性和准确性。

1 基本原理

1.1 CEEMDAN核心理论

CEEMDAN本质上属于EMD的一种，是一种噪声辅助分析方法。它的优点在于克服了模态混叠效应，可以精确重构出原始信号。算法具体如下：首先定义(·)为给定信号的第个IMF分量的算子，()表示高斯白噪声，其中=1,2,…,;表示在每个阶段的信噪比，其中=1,2,…,。设()为目标信号，CEEMDAN分为以下6个步骤：

(1) 将加入不同噪声的信号重复EMD分解次，计算集合平均值，目标信号()的第一模态固有分量为：

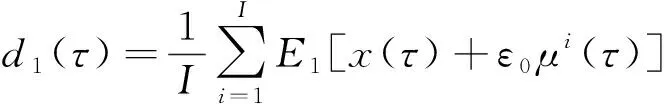
(1)

(2) 当=1时，计算一阶残差为：

()=()-()

(2)

(3) 对()添加经EMD分解后的噪声分量[()]，再进行EMD分解，第二阶固有模态分量为：

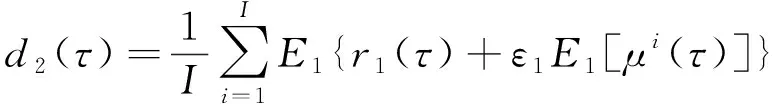
(3)

(4) 当=2,…,时(其中，是模态总体数量)，计算阶残差为：

()=-1()-()

(4)

(5) 使用EMD获取()+[()]的IMF分量，第+1阶固有模态分量为：

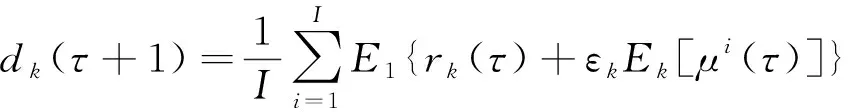
(5)

(6) 重复上述步骤(4)，直到所有余量不能进行EMD分解为止。

通过上述计算步骤可以看出，CEEMDAN是完备的，可以精确重构出原始信号，用做后续分析。

1.2 FRFT定义及相关理论

FRFT作为一种广义的傅里叶分析方法，信号的FRFT可以看作将信号的坐标轴在时频平面上绕原点做逆时针旋转。如果将信号的FT变换看成其由时间轴上逆时针旋转π/2后到频率轴上的表示，FRFT则可以看成信号在时间轴上逆时针旋转角度得到的轴的表示。任意信号()的FRFT定义为：

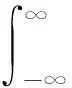
(6)

式中：为FRFT的变换阶数，可以为任意实数；=π2；[·]为FRFT的算子符号；(,)为FRFT的变换核：

(,)=

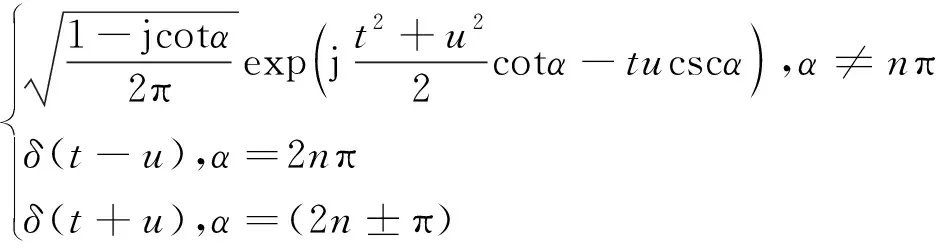
(7)

另外FRFT具有线性叠加和阶数叠加等性质。

浙江省农村宅基地“三权分置”的实践与思考（宋迎新等） ..........................................................................4-32

由定义可知，LFM信号只在适当分数傅里叶域中是一个冲激函数，因此只在该分数傅里叶域具有最好聚集特性，一个有限长的LFM信号在时频平面呈现斜直线的背鳍形状。FRFT本质上是信号的旋转，因此只要将信号旋转合适的角度，其幅度会出现明显的峰值，而白噪声则不会出现峰值，因此FRFT非常适用于处理LFM信号。

利用FRFT实现LFM信号参数估计的基本思路是，以旋转角度作为变量，对LFM信号做FRFT变换，形成信号能量在(,)的二维分布，=2π，如图1所示。

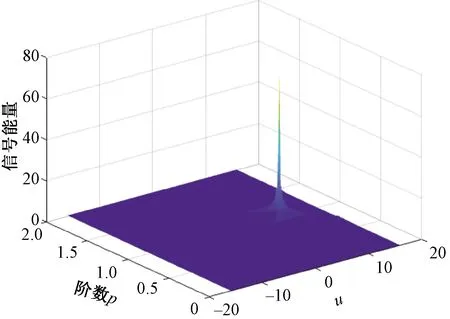
图1 FRFT能量聚集尖峰示意图

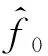
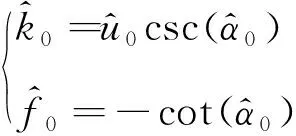
(8)

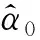
但在实际应用过程中，需要采用数字信号处理方式，目前大多采用了Ozaktas等提出的基于FFT的离散FRFT快速算法，该算法实现了量纲归一化，使得FRFT在实际中得到了广泛应用，本文同样采用上述离散算法。

由于峰值搜索是一个二维搜索问题，当参数估计要求精度高的时候，计算量很大。因此本文采用拟Newton法完成迭代搜索。具体思路如下，首先对变量和按照大的搜索步长直接搜索，得到初略估计，随后按照这一初始值，采用拟Newton法进行迭代搜索，得到参数的精确估计，其迭代过程表示为：

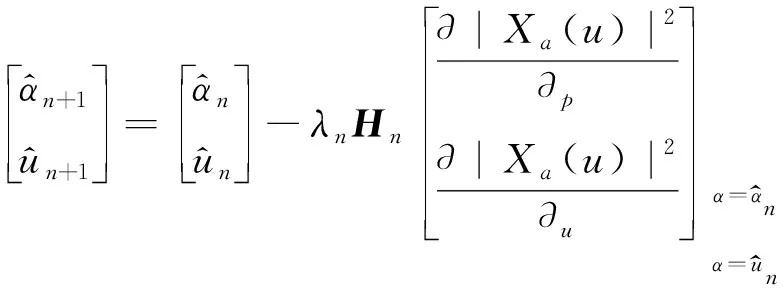
(9)

拟Newton法有效降低了二维搜索算法的复杂度。

2 基于CEEMDAN和FRFT的多分量LFM信号参数估计

多分量LFM信号参数估计方法流程如图2所示。首先对LFM信号做CEEMDAN分解，获得从高频到低频排列的IMF分量，随后对每个IMF分量做傅里叶变换，得到每个分量的幅值方差，计算所有方差平均值，比较每个方差值和方差平均值的大小关系，分离出有用IMF分量，重构有用IMF分量得到去噪后的信号，再利用FRFT估计各个分量参数。其中采用了分离技术和拟Newton法，有效提高了该方法的可靠性并降低了计算的复杂性。

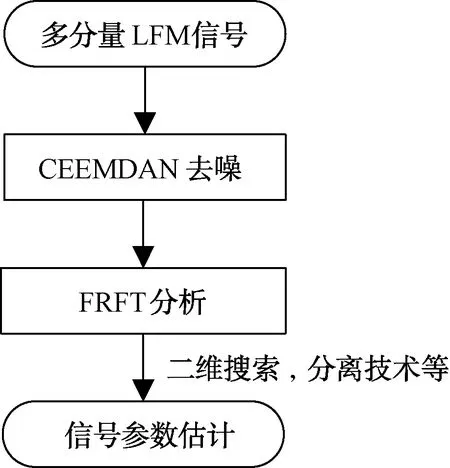
图2 方法流程图

2.1 CEEMDAN分解和重构

CEEMDAN作为一种非平稳非线性的信号分解方法，可以把复杂信号分解为一系列不同尺度的固有模态函数，每个IMF分量包含的频段随信号自适应变化，非常适用于LFM这类非线性信号。采用CEEMDAN分解去噪的原理是去掉包含噪声的IMF分量，随后重构信号，因此准确分离出噪声IMF分量和有用信号IMF分量非常重要。目前常用方法有排列熵、自相关函数、互相关系数等。排列熵需要计算每个IMF分量的熵值，计算较为复杂；自相关函数要求取每个IMF分量自相关曲线的主瓣宽度，经过对LFM信号的验证，此方法效果较差；互相关系数法是通过计算每个IMF分量和原始信号的相关系数大小进行去噪，对于非平稳非线性信号降噪效果较差。经过对比，本文采用基于IMF的频谱幅值方差大小作为判断依据，有用信号IMF分量频率成分幅值较为单一，噪声IMF分量幅值较为杂乱，因此可以通过计算所有IMF分量的方差来判断。方差反映的是数据的离散化趋势，方差越大表明数据波动越大。如果某一个IMF分量幅值方差较大，可以认为是噪声IMF分量，相反则认为是有用IMF分量。随后重构有用IMF分量，得到去噪后的信号。

2.2 FRFT应用

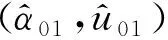
3 仿真分析

为了验证上述方法的可靠性和准确性，下面建立仿真实验进行验证，LFM信号中各分量参数见表1，并在信号中加入5 dB的高斯白噪声，按照上述方法流程对信号进行处理。

表1 LFM信号各分量参数

首先对信号做CEEMDAN分解，分解后的10个IMF分量如图3所示。并计算每个分量的傅里叶频谱方差值，如表2所示。方差平均值=326，取幅值方差大于的IMF分量作为重构分量，累加重构分量得到重构信号。

图3 多分量LFM信号CEEMDAN分解

表2 IMF分量傅里叶变换幅值方差大小

分别对仿真信号和重构信号做FRFT变换，分数阶频谱三维图分别如图4(a)和图4(b)所示。从图4(a)中可以看出，仿真信号包含2个峰值点，信号的能量在此旋转角度得到良好的聚集，表明LFM信号中含有2个分量，在经过CEEMDAN分解重构后，FRFT频谱图如图4(b)所示，从图4可以看出，重构信号的能量峰值依然突出，但在底层能量分布较为光滑，表明CEEMDAN分解重构有效地减小了噪声干扰。

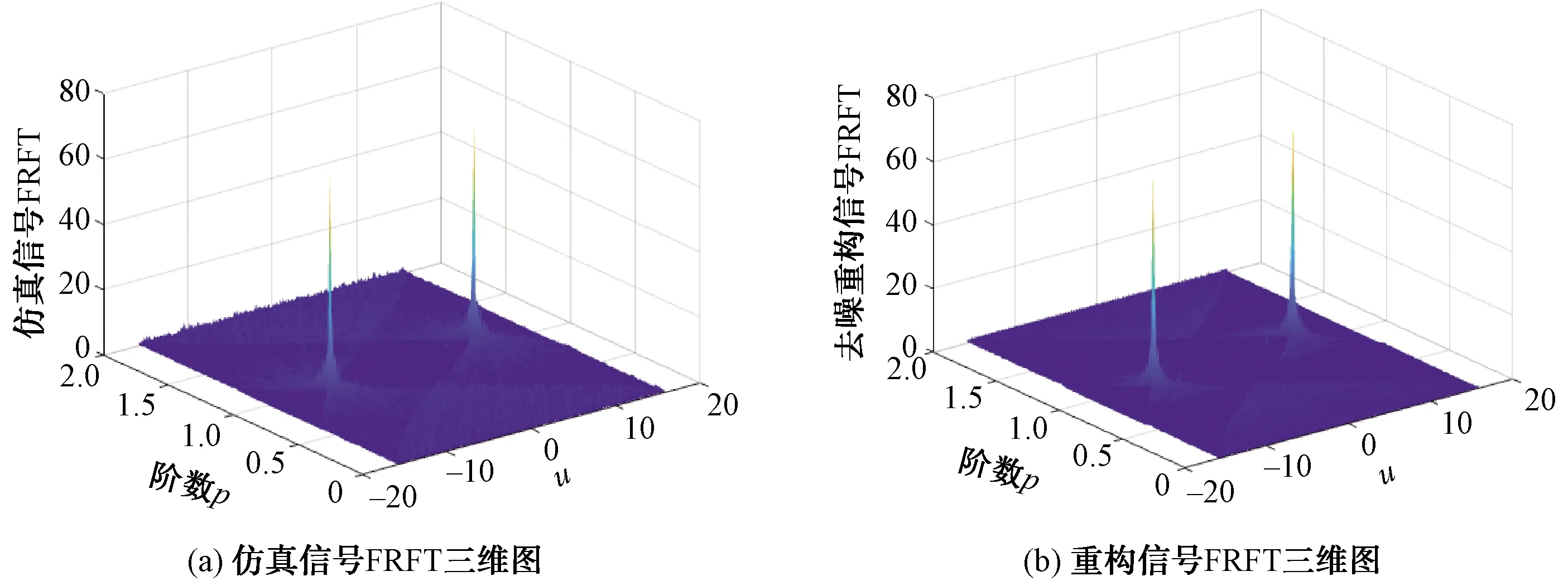
图4 CEEMDAN去噪对比

按照本文方法，对重构信号做FRFT处理，如图4(b)所示。采用二维搜索和拟Newton法，找到峰值最大点，最大峰值点对应的阶数为=1.063。因此根据公式(8)，第一分量的起始频率为=3.004 7 MHz，调制斜率为=0.990 0 MHz·μs。随后在域采用汉宁窗对该分量进行窄带滤波，对滤波后的信号做-阶的FRFT，反向旋转到原来的时间域，再做FRFT处理，找到峰值最大点对应的阶数=1.126，得到第二分量的起始频率=1.999 0 MHz和调制斜率=2.005 5 MHz·μs。按照上述步骤，取输入信噪比的变化为-20～20 dB，间隔2 dB，分别运行1 000次蒙特卡罗模拟，并计算各分量参数的估计均方差。为了体现本文方法的可靠性，同时对仿真信号做传统FRFT处理，最后对2种方法的估计均方差进行对比。2种方法的调频率和起始频率均方误差估计如表3～表6和图5～图6所示。

表3 第一分量参数频率f0的不同信噪比估计均方差

表4 第一分量参数斜率k0的不同信噪比估计均方差

表5 第二分量参数频率f1的不同信噪比估计均方差

表6 第二分量参数斜率k1的不同信噪比估计均方差

为了突出2种方法参数估计结果差异，按照不同信噪比范围对参数估计结果进行对比。当信噪比在-20～-10 dB之间，传统FRFT和CEEMDAN+FRFT两种方法的所有参数估计均方误差如表3～6所示。从图中可以看出基于CEEMDAN+FRFT的参数估计准确率比传统FRFT方法要高。当信噪比在-8 dB和20 dB之间时，2种方法估计结果如图5～6所示。第一分量2种参数的估计结果如图5所示。当信噪比小于4 dB时，基于CEEMDAN+FRFT方法与传统FRFT方法相比，其参数估计精度较高；当信噪比大于4 dB时，2种方法估计精度相差不大，估计结果都非常准确。第二分量的2种参数估计结果如图6所示，根据图中对比结果，2种方法的估计精度相差较大。上述所有结果表明CEEMDAN+FRFT可以有效提高参数估计性能。

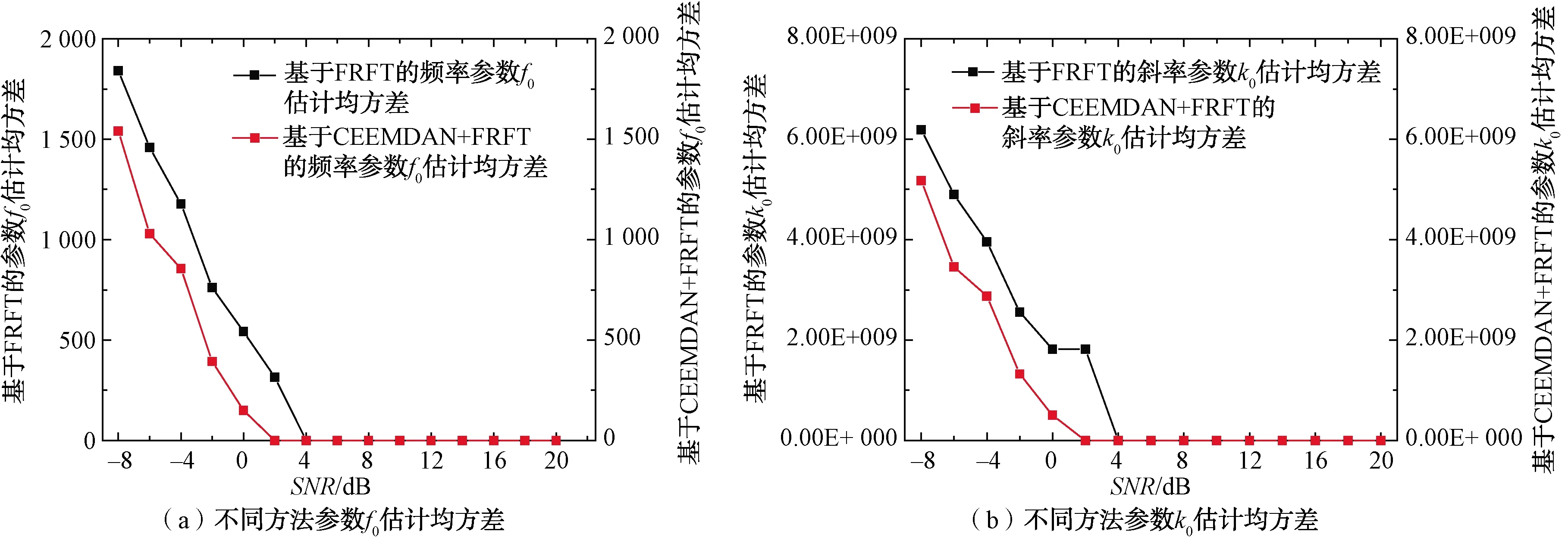
图5 第一分量2种参数不同方法估计均方差对比

图6 第二分量2种参数不同方法估计均方差对比

4 结束语

本文针对多分量LFM信号参数估计问题，提出了一种新的参数估计方法。该方法通过对信号做CEEMDAN分解，利用IMF方差作为判定依据，得到去噪后的重构信号，最后利用FRFT的相关特性，并在处理过程中引入分离技术和拟Newton法，提高了参数估计精度。仿真实验结果表明，与传统的FRFT方法相比，该方法能有效去除噪声的干扰，不需要针对不同信号设置不同门限，具有一定普适性，有效提高了参数估计的可靠性。