一种基于稀疏表示与聚类的辐射源智能识别方法

沈佳琪，罗宇轩，杨 帆

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

在现代电子战中，信号样式不断增多，电磁环境日益复杂，使辐射源识别越来越困难。首先，时、空、频雷达信号交错，设备种类繁多，信号调制样式快捷多变，信号密度大，甄别困难；其次，目标识别要求实时性与准确性，要求快速精准打击；还有最重要的一点是，缺少高质量的辐射源数据，也就是说缺少带有专家标签的数据。针对上述问题，本文采用了一种替代策略，通过使用基于少量标签样本训练的监督网络对辐射源信号进行稀疏表示，将其降维至一个平滑的较小空间中进行信号样本聚类。把样本识别问题转换为集群识别问题，降低了工作量，可用于海量数据的识别。在该特征空间中，相似或相同类型的样本之间距离较小，不同类型信号样本之间距离较大，信号样本形成彼此易于区分的可分离集群。

1 稀疏表示

1.1 特征提取

通过卷积神经网络来降维原始采样信号以获得其稀疏表示，卷积运算的平移不变性十分适合处理时序信号，局部感知能力也有助于网络学习信号细微特征。

本文针对辐射源信号识别问题，设置了9种辐射源信号，如表1～表3所示。

表1 线性调频信号参数表

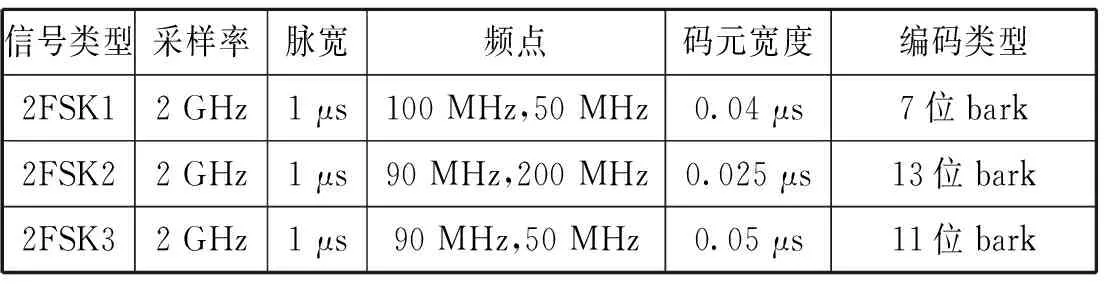
表2 二频编码信号参数表

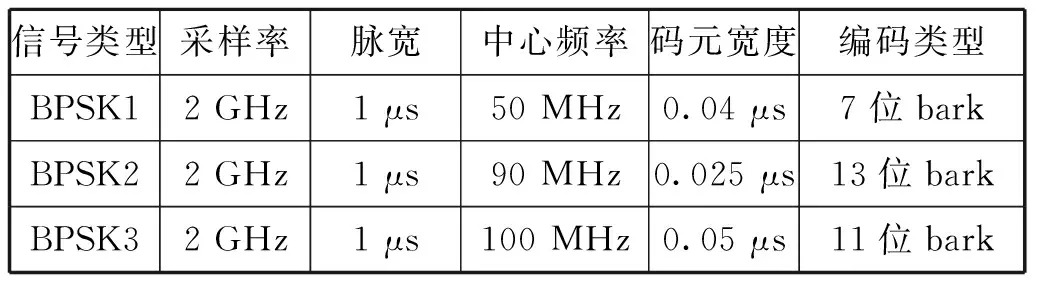
表3 二相编码信号参数表

以上9类信号在信噪比为10 dB情况下每类生成1 000个信号样本，作为训练集与验证集。再在不同信噪比下，每类生成30个信号样本共270个样本，用于测试集。

采用的卷积神经网络(CNN)结构如图1所示。

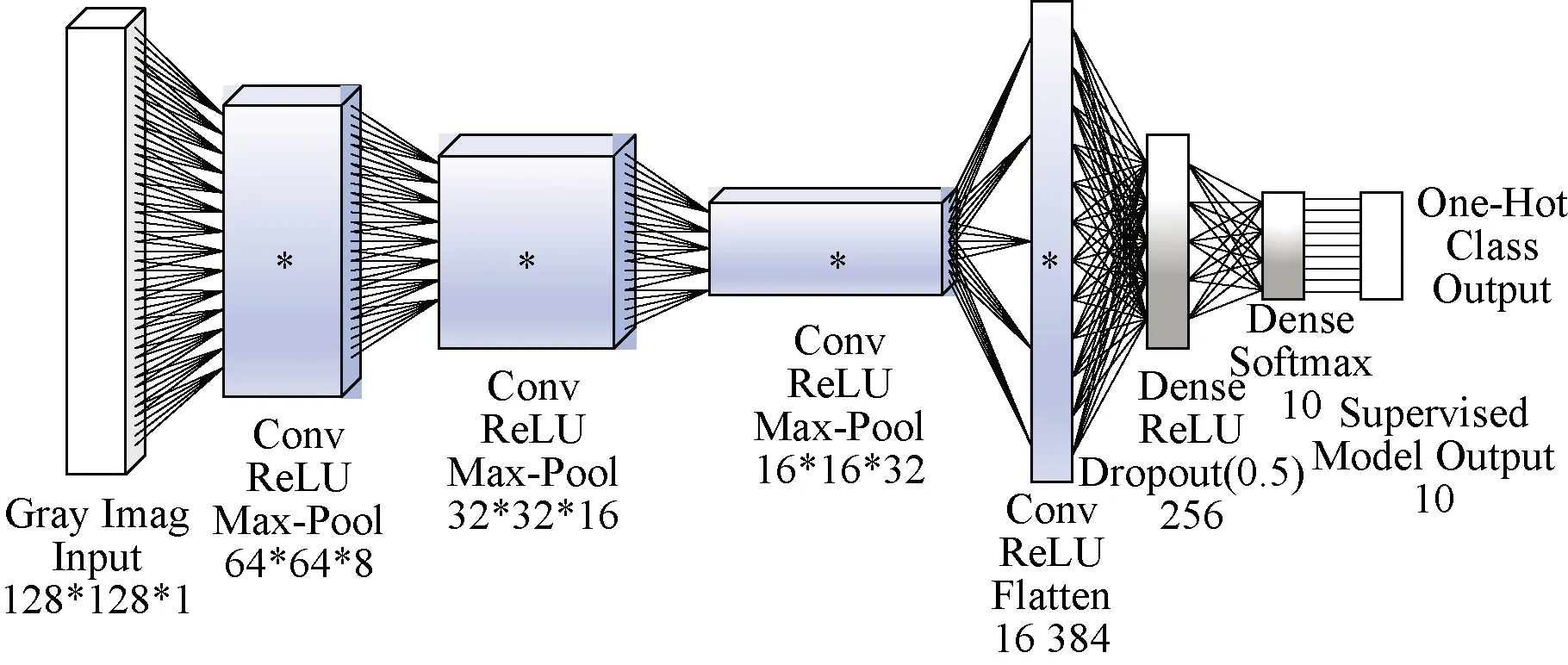
图1 CNN结构

采用了4个卷积块，如图中标“*”的部分，卷积核均为3×3，个数依次为8、16、32、64递增，padding设置为same。池化采用最大池化，范围为2×2。最后连接一个256个神经元的全连接层，采用Dropout层缓解过拟合，最后通过softmax进行分类。使用一部分经过专业标记的数据，通过监督训练使学习过的标签类别具备很好的分类效果，并且会泛化，提供在特征空间中分隔没有标签的其他类别的能力。

网络中采用线性整流函数(ReLU)作为激活函数。激活函数为：

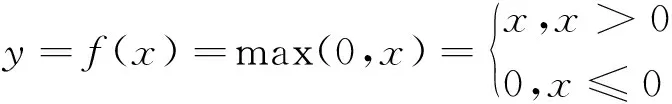
(1)

ReLU是一种常用的激活函数，其函数图像如图2所示。

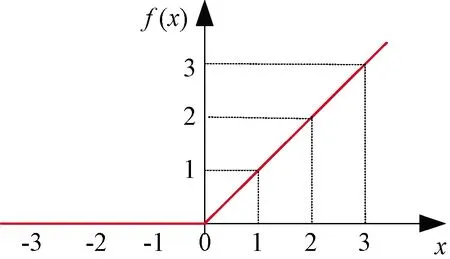
图2 ReLU函数图像

在神经网络中，对于进入神经元的来自上一层神经网络的输入向量，使用线性整流激活函数的神经元输出为max(0,+)。

标准的sigmoid函数不具备稀疏性，需要用一些惩罚因子来训练出一大堆接近0的冗余数据，从而产生稀疏数据，而ReLU的作用是如果计算出的值小于0，则输出0，否则保持原来的值不变。

除了使用ReLU作为线性整流函数，以及最大值池化(Max-Pooling)做采样外，还使用了Dropout技术提高模型的泛化性，缓解过拟合现象。过拟合具体表现在：模型在训练数据上损失函数较小，预测准确率较高；但是在测试数据上损失函数比较大，预测准确率较低。为了解决过拟合问题，一般会采用模型集成的方法，即训练多个模型进行组合。此时，训练模型费时就成为一个很大的问题，不仅训练多个模型费时，测试多个模型也很费时。

综上所述，训练深度神经网络的时候，总是会遇到两大难点，即容易过拟合与费时。Dropout可以比较有效地缓解过拟合的发生，在一定程度上达到正则化的效果。图3为Dropout的可视化表示。

图3 Dropout前后神经元

图3(a)是应用Dropout之前的网络，图3(b)是应用了Dropout的同一个网络。Dropout的思想是训练整体深度神经网络，并平均整个集合的结果，而不是训练单个深度神经网络。网络以概率舍弃部分神经元，其它神经元以概率=1-保留，舍去的神经元的输出都设置为零。

在标准神经网络中，各个参数的导数引导参数改变，使损失函数减少，因此神经元可以通过这种方式修正其它单元的错误。Dropout在实践中能很好工作的原因是其在训练阶段阻止了神经元的共适应。

没有Dropout的网络计算公式如下：

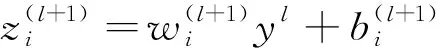
(2)

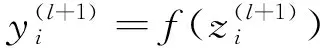
(3)

式中：()为激活函数。

采用Dropout的网络计算公式如下：

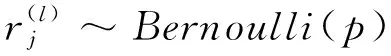
(4)

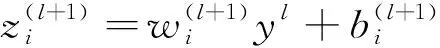
(5)

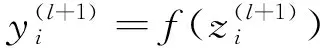
(6)

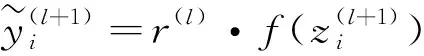
(7)

由于在训练阶段神经元以概率保持，在测试阶段必须仿真出训练阶段使用的网络集的行为。因此，测试阶段需要通过系数来缩放激活函数：

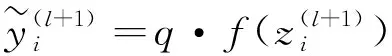
(8)

对上述网络以CNN训练，采用分类交叉熵函数作为损失函数，优化器选用Adam。训练200代，训练过程中损失与准确率变化如图4所示。

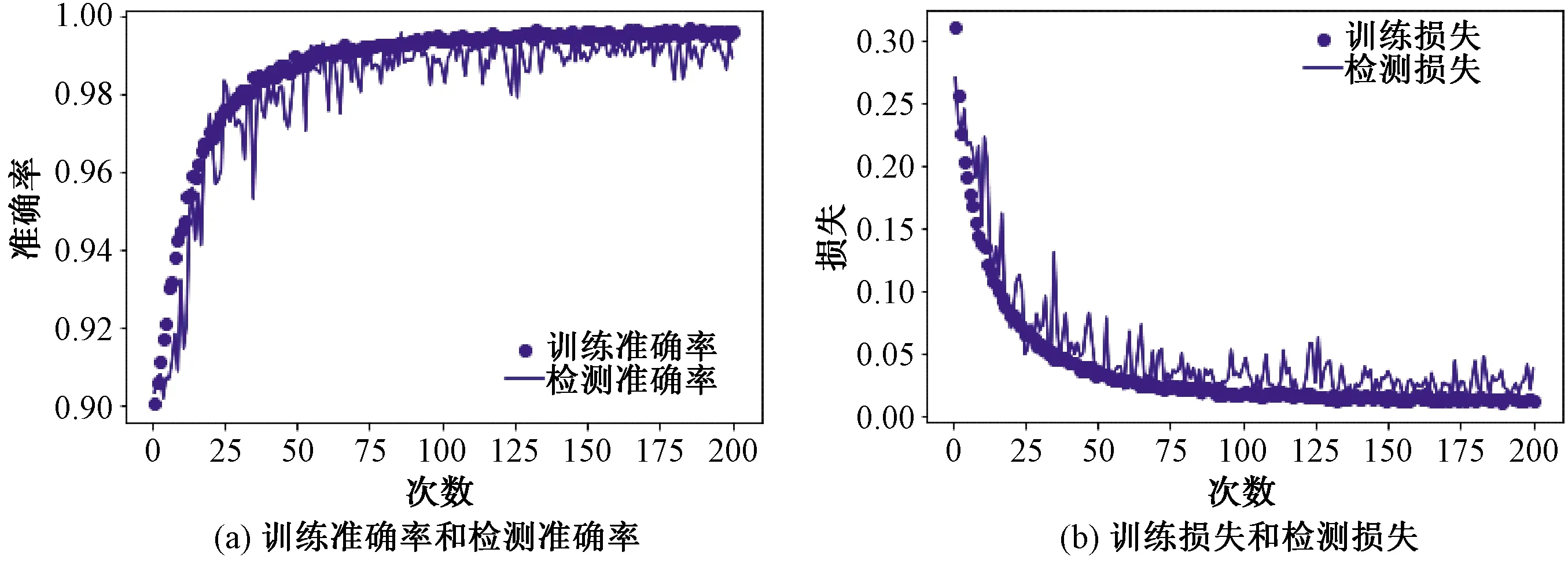
图4 CNN训练损失及精度变化

为了便于观察，对其进行平滑处理,如图5所示。

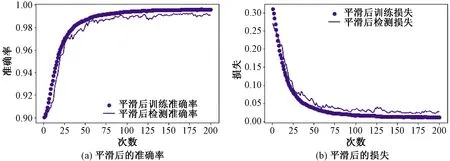
图5 平滑后CNN训练损失及精度变化

可以观察到：在125代以后，网络在验证集上的精度与损失已经几乎不变。使用回调函数，以最小化验证集损失为原则保存模型，最终测试精度为0.995 2，损失为0.006 8。

1.2 可视化嵌入

为了可视化这些稀疏表示对信号类型的可分离性，采用t-分布邻域嵌入算法t-SNE(t-distributed stochastic neighbor embedding)对50维稀疏表示进一步降维，对样本分部二维可视化展示。图6为t-SNE原理框图。

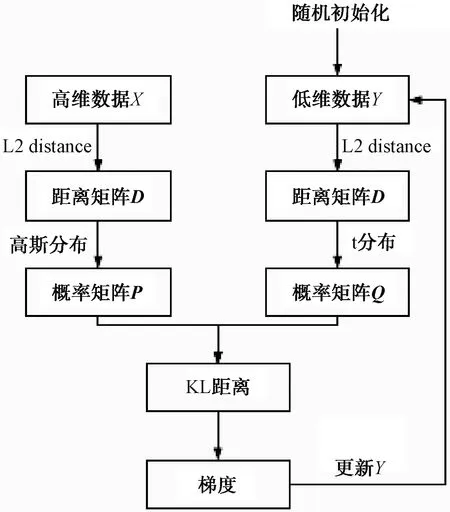
图6 t-SNE原理框图

SNE通过仿射变换将数据点映射到概率分布上，主要包括：

(1) 构建一个高位对象之间的概率分布，使得相似的对象有更高的概率被选择，不相似的对象被选择的概率较低。

(2) 在低维空间里构建这些点的概率分布，使这2个概率分布尽可能相似。

低维空间下使用更重长尾分布的t分布代替高斯分布，避免拥挤问题和优化问题，受异常值影响更小，拟合效果更为合理，较好地捕捉了数据的整体特征。

对10 dB信噪比测试集中270个样本使用训练好的CNN提取其稀疏表示，并使用t-SNE进行二维可视化，结果如图7所示。

图7 二维可视化的样本分布

可见所有样本在特征空间中均形成了可分离的聚类簇。

1.3 泛化性测试

为了验证该方法对未参与训练信号类型的泛化性，稀疏表示的信号特征可以使用引导方法以半监督的方式帮助区分新的未知信号类型。重复之前的实验，使用9类信号中的6类训练监督分类器，LFM3、2FSK3和2PSK3 3类信号不参与训练，生成网络后对所有9类信号进行稀疏表示提取特征图，并使用t-SNE可视化，结果如图8所示。

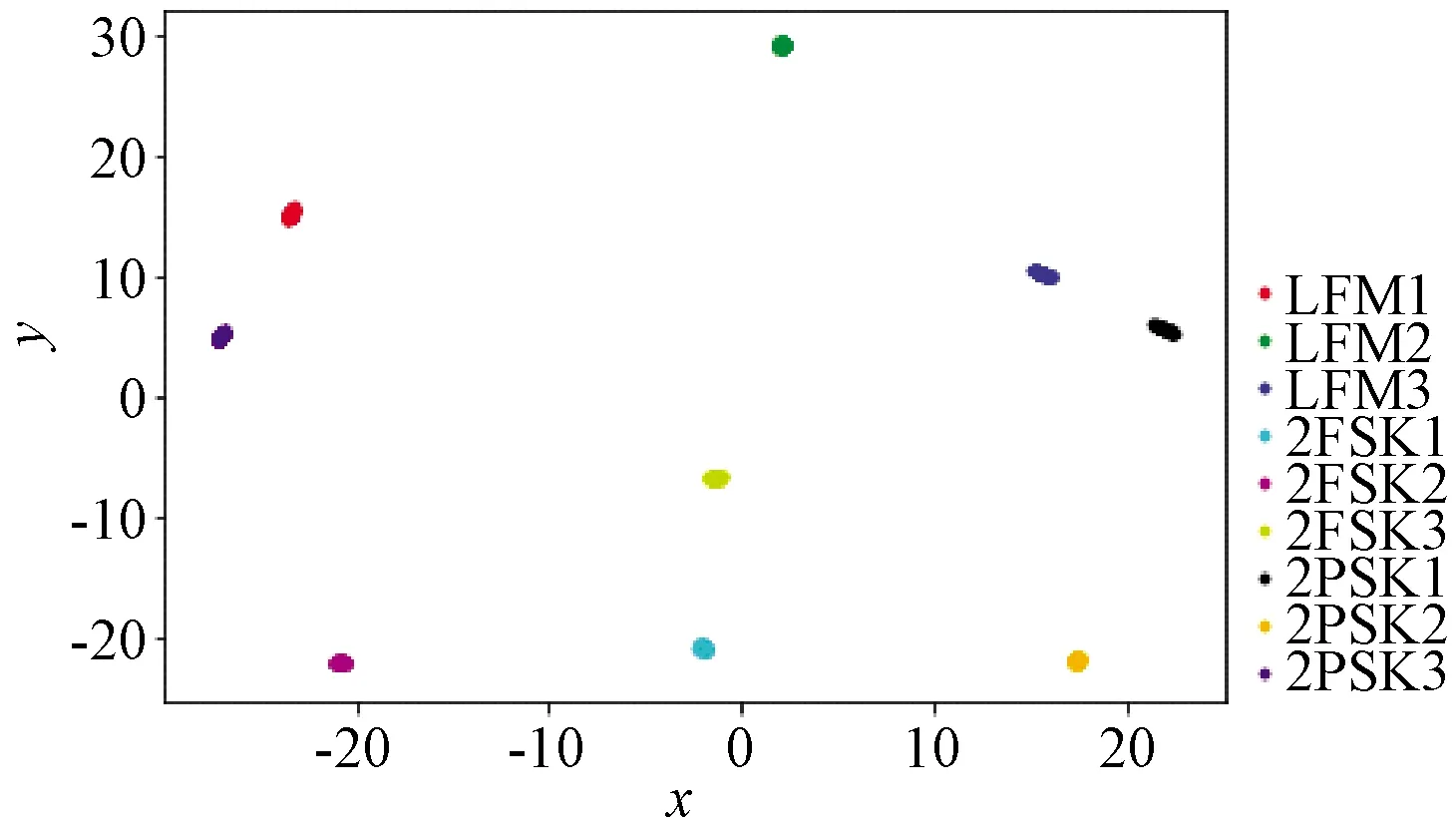
图8 泛化性测试样本空间

由检查结果不难发现，无论是已训练过的信号类型还是未参与训练的信号类型，都在嵌入空间中形成了明确可分离的聚类簇，说明稀疏表示确实有泛化能力，可用于识别和聚类。

2 聚类算法

当样本在嵌入空间中形成相对分离的群集，就可以使用任意群集算法将他们分组并分配一个类标签。对每组抽取一定数量的样本进行精确识别，结果视作群集的类标签，或在需识别数据中混入一些已识别样本，根据群集中已标识样本，决定群集标签。

采用DBSCAN(Density-Based Spatial Clustering of Applications with Noise)聚类算法，将群集分为若干组未知但不同的信号类型。直观效果上看，使用该算法可以找到样本点全部密集区域，对远离密度核心的噪声点鲁棒，无需知道聚类簇数量且可以发现任意形状的聚类簇。图9为DBSCAN中点的类型与关系。

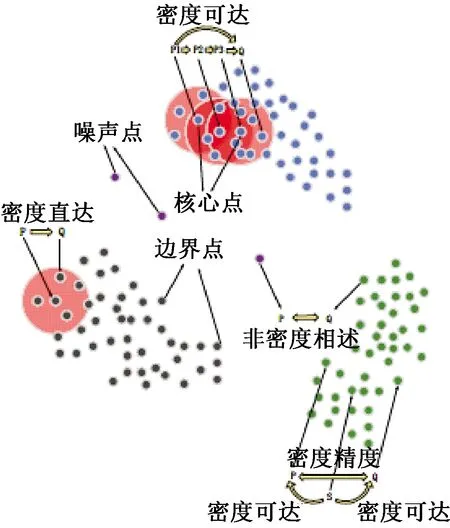
图9 DBSCAN中点的类型与关系

DBSCAN算法将点分为3个类别，领域半径内样本点数大于minpoints(最小样本点)的点叫核心点；不属于核心点但在某个核心点邻域内的点叫边界点；既不是核心点也不是边界点的是噪声点。算法步骤分为2步：

(1) 寻找核心点形成临时聚类簇，扫描全部样本点，将核心点纳入核心点列表，并形成对应的临时聚类簇。

(2) 合并临时聚类簇，检查每一个临时聚类簇中的点是否为核心点。如果是，则将该点对应的临时聚类簇与当前临时聚类簇合并，得到新的临时聚类簇。重复操作直至当前临时聚类簇中每一个点或不在核心列表，或密度直达点已在该临时聚类簇，则该临时聚类簇升级为聚类簇。

对嵌入空间中信号样本进行聚类处理，结果如图10所示。

图10 聚类前后样本空间

实验采用之前训练的9类一维CNN网络，处理测试集为-5 dB信噪比条件下9类信号各30个共270组样本。图10(a)为各样本稀疏表示的二维嵌入，图10(b)为对嵌入空间样本进行DBSCAN聚类结果。可以发现，空间中样本被聚类为9种未知类型，虽然由于信噪比降低稀疏表示质量变差，导致少数样本被错误聚类，但结果足以说明基于稀疏表示的聚类算法适用于辐射源信号识别。

3 高训低测实验

实际使用中一般采用高信噪比样本进行训练，目的是网络尽量学习到信号的特征而非噪声的特征，进行预测的时候希望网络能适用于低信噪比的信号。因此，设计一组高信噪比训练、低信噪比测试的实验来探究方法性能极限。

图11～图18为1组仿真结果，左图均为t-SNE后嵌入空间样本分布；右图均为DBSCAN聚类结果，采用超参数均为邻域范围=1，最小样本点数=10。

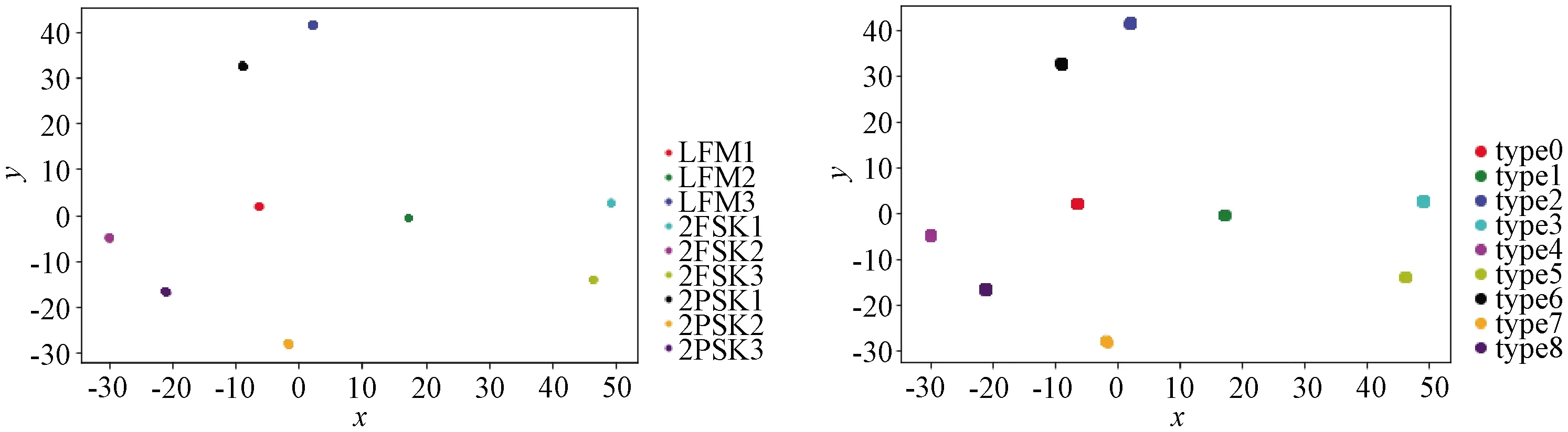
图11 10 dB信噪比实验

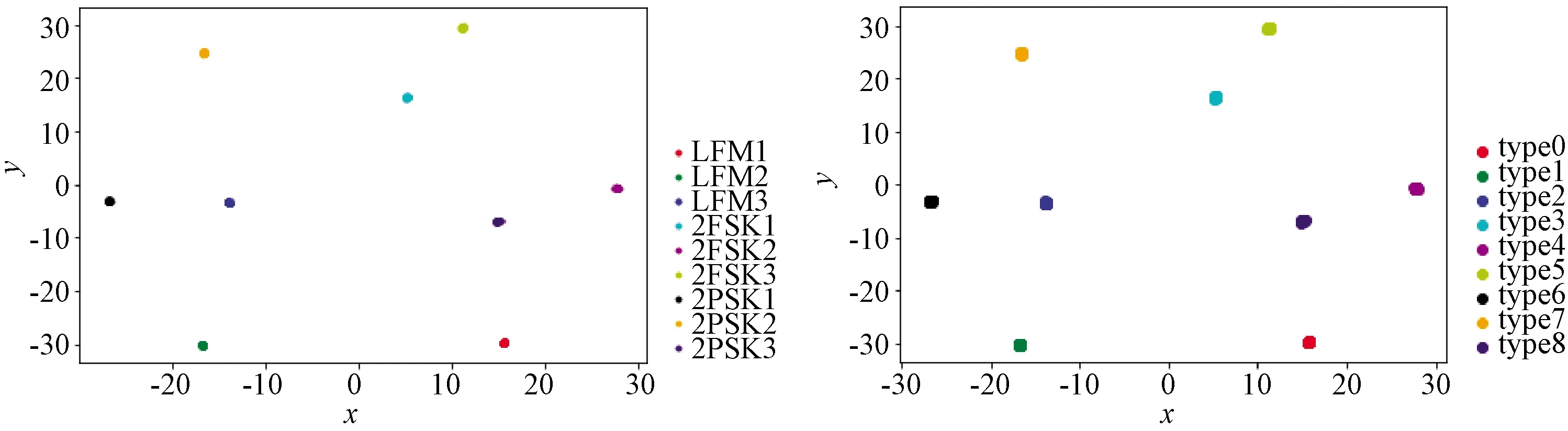
图12 5 dB信噪比实验

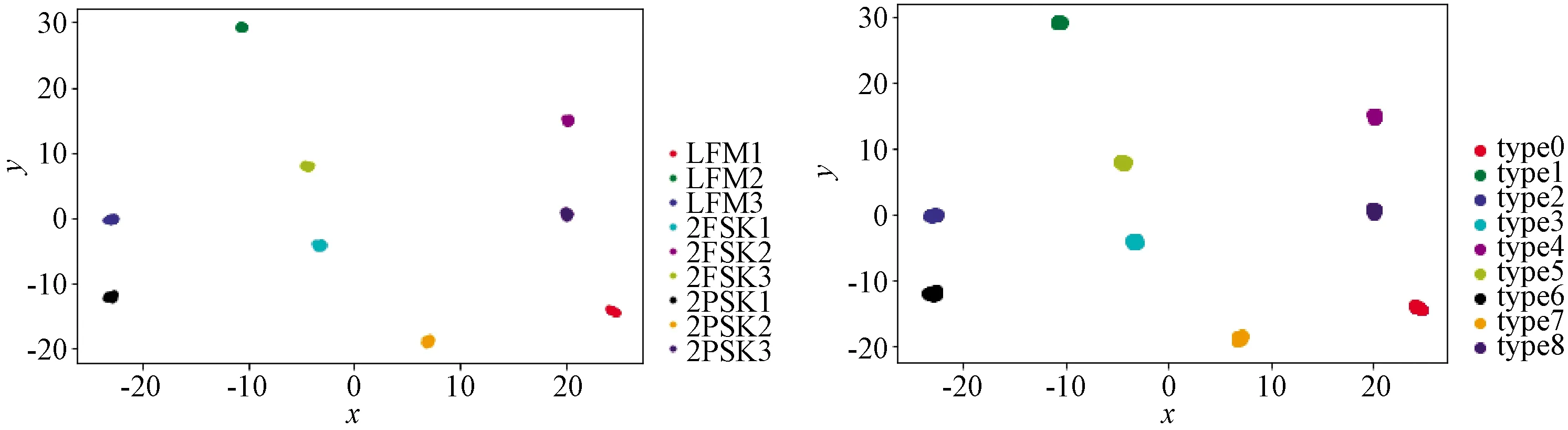
图13 0 dB信噪比实验

图14 -4 dB信噪比实验

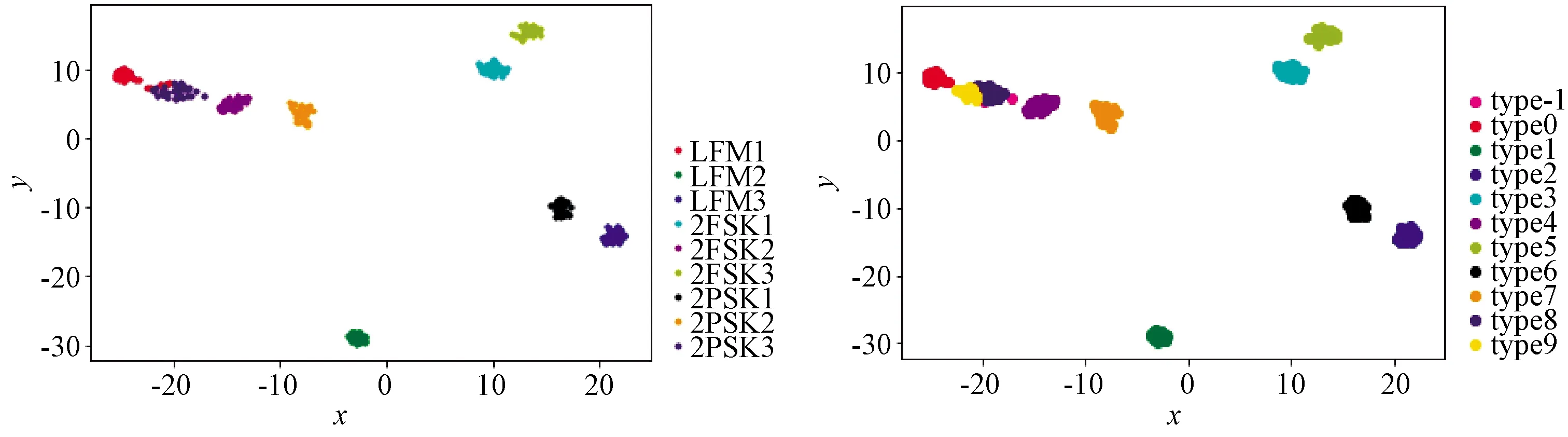
图15 -5 dB信噪比实验

图16 -6 dB信噪比实验

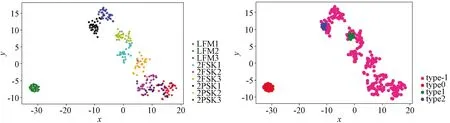
图17 -8 dB信噪比实验

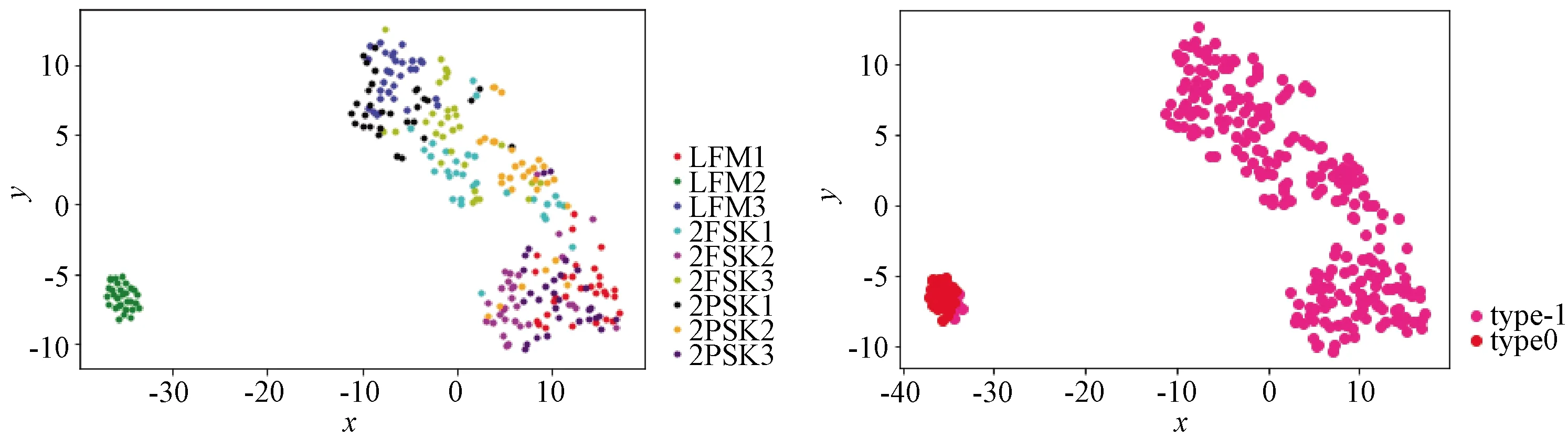
图18 -10 dB信噪比实验

根据以上仿真结果发现，该方法在-4 dB信噪比以上的情况下能够无错分类，效果良好。而训练的一维CNN网络，在0 dB信噪比时已出现错误分类情况。-4 dB信噪比时该方法出现了噪声点(type-1)。-5 dB信噪比时出现了错误聚类以及多对类型，但仍有很好的分类效果。-6～-8 dB信噪比之间，噪声点增多，对比左图嵌入空间中各类别信号仍有聚集性，此时如果适当放大DBSCAN算法超参数，应该会有更好的聚类效果。-6～-8 dB信噪比之间噪声点急剧增多，嵌入空间中样本已经混杂，无法有效聚类识别。

该方法是一种划分信号集后识别处理，规定识别正确如下：聚类算法后某一位置类型样本80%属于同一类型信号，则认为聚类成功，该类信号样本数集为正确分类个数。由于t-SNE算法具有随机性，其本身是一个非凸优化问题，所以会有局部最优解。因此采用每种信噪比各进行100次Monte Carlo实验，以每次结果的平均正确率作为该方法在此信噪比情况下的分类准确率。曲线如图19所示。

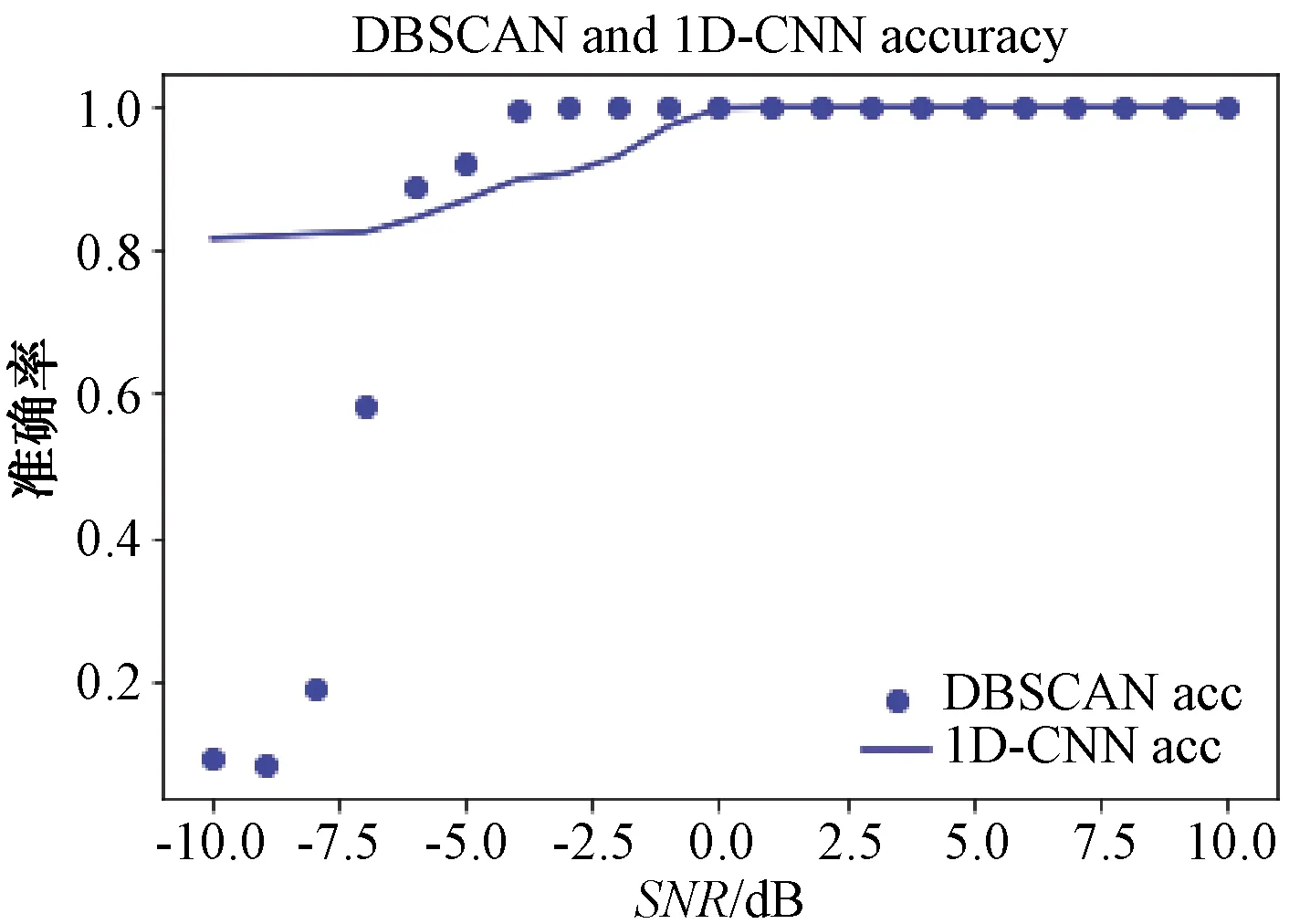
图19 DBSCAN与一维CNN识别准确度对比

在-6～0 dB信噪比情况下，本文方法比一维CNN直接识别准确率更高，在此情况下信号稀疏表示比分类器更加可靠。而当信噪比继续降低，本方法分类准确率急速下降，说明此方法对信噪比更为敏感。

4 结束语

本文主要证明了在原始采样的辐射源信号上通过卷积神经网络学习得到的稀疏表示可有效地聚类不同类型的辐射源信号，通过少量标记数据进行训练，即可应用于大规模数据的识别。虽然相比分类器识别，本方法对信噪比的变化更为敏感，但考虑到应用本方法可将针对信号样本的识别问题转换为针对信号集群的识别，所以具有实用价值。