基于遗传算法优化BP神经网络的辐射源威胁等级评估方法

陈金炜，柴 恒

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

对于威胁等级不同的多个目标雷达，需要实施不同优先级别的干扰措施。在雷达对抗干扰中，准确合理的雷达辐射源威胁等级判决，是干扰决策的重要基础。因此，合理的雷达威胁等级判定是有效进行电子干扰的前提与保证。

近年来，人工智能技术在雷达对抗领域应用广泛，而神经网络是人工智能领域的重要组成部分，有研究人员尝试将神经网络用于辐射源威胁等级评估。但是，神经网络存在着一些不可避免的缺陷。以BP神经网络为例，随着数据特征维度的增加，网络的学习收敛速度会大幅降低，导致学习性能变差。

遗传算法(GA)是一种通过模拟自然进化过程搜索最优解的方法,属于群智能算法。文献[5]研究了群智能算法在目标识别中的应用。本文采用遗传算法来优化反向传播(BP)神经网络，遗传算法优化BP神经网络的目的是通过遗传算法得到最优的网络初始权值和阈值，然后采用此初始权值和阈值来构造BP神经网络。在此基础上建立基于遗传算法优化BP神经网络的辐射源威胁判决模型，提出基于遗传算法优化BP神经网络的辐射源威胁等级评估算法，即遗传算法神经网络(GANN)算法。

1 辐射源威胁分析

1.1 传统的辐射源威胁分析方法

在传统的威胁评估方法中，比较常用的是多属性决策(MADM)方法，此方法源于JDL(Joint Directors of Laboratories)信息融合模型。该方法根据辐射源威胁等级评判的特点，采用一致性检验的方法，确定每个辐射源信号参数或威胁因子各自的权重，进而再通过加权的方法，结合评判标准，给出相应的辐射源威胁等级。

在基于多属性决策的威胁判决方法中，主要考虑3个辐射源参数进行威胁大小评估：重频(PRF)、载频(RF)、脉宽(PW)，而依据上述参数进行威胁评估的依据如下：

(1) 一般来说，敌方雷达脉冲重频增大是一个危险信号，表明敌机已经逼近或者已锁定我机(舰)。也就是说，重频越高，威胁越大。

(2) 频率越高，其探测精度越高，同时其探测距离越小。也就是说，载频越高，威胁越高。

(3) 脉宽越宽，雷达分辨率越大，经度越低；脉宽越窄，雷达分辨率越小，经度越高。因此，脉宽越窄，威胁越大。

根据以上依据可以为各个参数建立一个威胁隶属度函数，利用威胁隶属度函数就可以计算出当前辐射源各个参数的威胁度。但是，用以判定辐射源威胁程度的参数，其各自的权重是不同的。权重是对参数重要性的量化表示，它的判定具有明显的模糊不确定性，是干扰决策中的一种综合化评判方法。对于权重的确定，传统的辐射源威胁等级判决方法中多使用层次分析法。

该方法根据辐射源威胁等级评判的特点，采用一致性检验方法，确定威胁因子的权重，进而通过加权给出辐射源威胁等级评判标准。此方法充分利用先验知识，减少实时分析过程，面对战场上众多的雷达辐射源，可以快速、高效、可靠地判断他们的威胁等级。但不可否认，该方法过于依赖单一维度的经验。

1.2 基于用途分析的威胁等级判定方法

传统的基于MADM的威胁判决方法仅依靠提取个别属性、建立隶属度函数、进行模糊处理的方法对辐射源威胁等级进行判定，虽然能够解决干扰资源调度问题；但是由于对提取数据的精确性要求较高，而实际提取的雷达数据量较大，存在多种干扰因素。同时，MADM方法过于依赖单一维度的经验，可能无法实现有效的威胁判决。

根据侦察接收到的脉冲信号特点，判断当前辐射源的类型或用途，进而作出威胁评估结果。这样的威胁评估过程应该更符合实际情况，因为辐射源的威胁大小本质上还是基于辐射源的类型或用途。因此，雷达辐射源威胁程度判决应当首先根据侦察数据和已掌握的雷达知识来分析当前雷达的用途。分析雷达用途的一般过程为：

(1) 判别雷达平台类型。对于地面雷达还应了解其部署的方向、位置及雷达阵地的特点。

(2) 根据雷达信号的特点，大致判别雷达的用途，主要依据的信号参数是工作频率、脉冲重复间隔、脉冲宽度、天线扫描特点等。

(3) 综合雷达的战术运用特点，判断雷达当前的工作状态。

基于用途分析时，辐射源的威胁等级划分如表1所示。

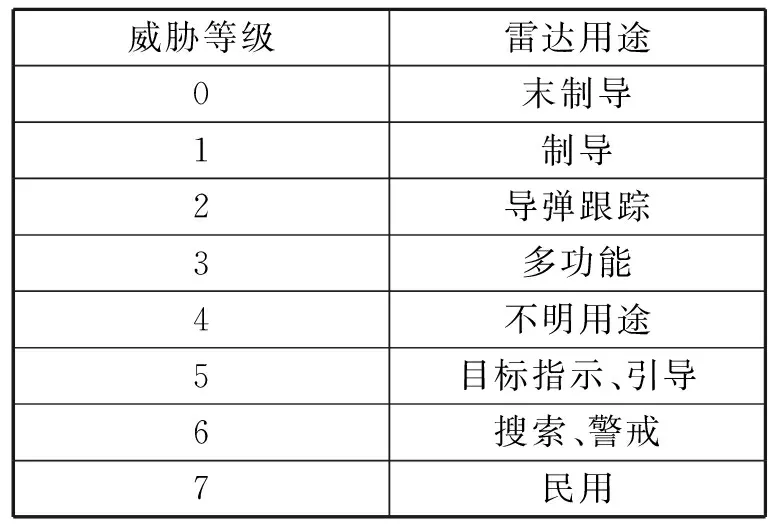
表1 威胁等级划分表

2 基于GANN的辐射源威胁等级评估算法

实验中采用基于用途分析的威胁等级判断方法，使用智能算法首先判断辐射源的功能或用途，再对威胁等级进行判定。本部分针对辐射源的威胁等级判决问题，以遗传算法和BP神经网络为基础，提出基于遗传算法优化BP神经网络的辐射源威胁等级评估算法，以下简称为GANN(genetic algorithmic neural network)算法。

2.1 遗传算法

遗传算法是一种通过模拟自然进化的方法来搜索最优解的一种方法。主要特点是直接对结构对象进行操作，不存在梯度求导机制和函数连续性的限定，主要是采用概率的方法来实现寻优的方法，自适应调整搜索的方向。

遗传算法主要由三大模块构成，即编码、个体适应度估计和遗传运算，遗传运算又包括染色体选择、交叉、变异等。改良的遗传算法都是简单遗传算法(SAG)的变异形式。在遗传算法中，定义种群或者群体为所有编码后的染色体的集合，表征每个个体的都是其相应的染色体。执行流程如图1所示。

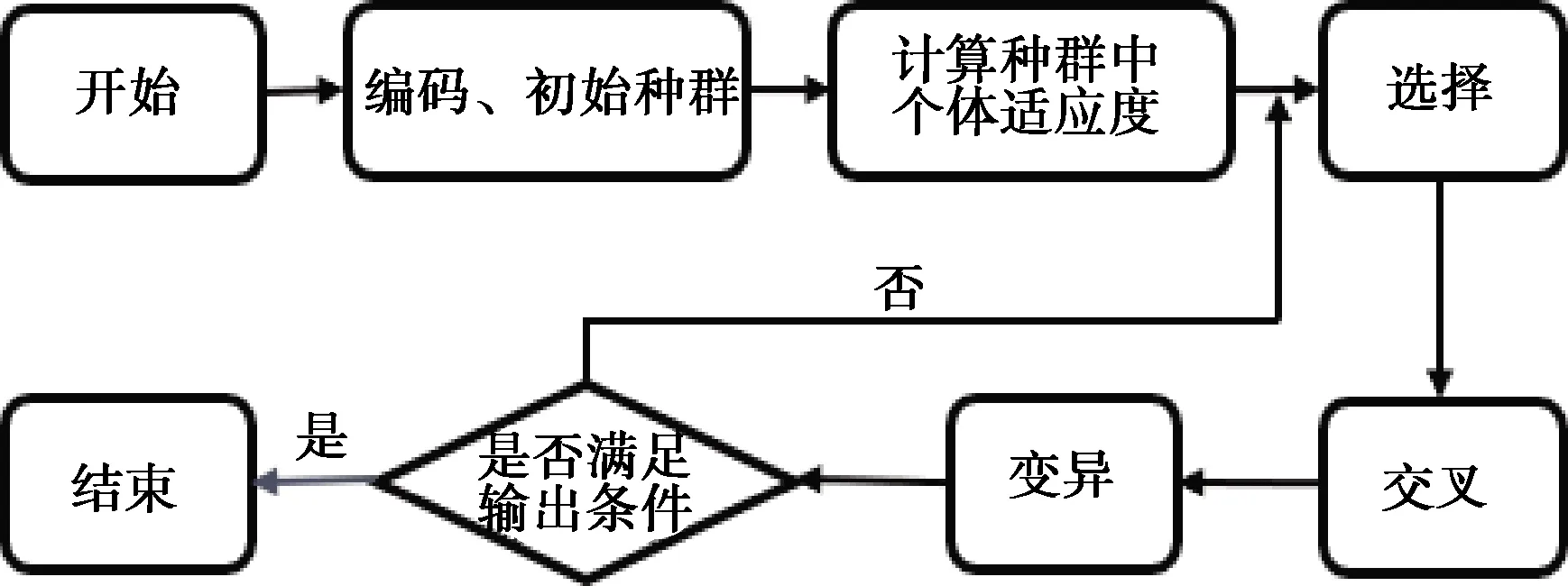
图1 遗传算法执行流程

2.2 BP神经网络

BP神经网络算法由正向传播与误差的后向反馈两个过程组成。正向传播是指在当前网络参数下由输入得到输出的过程，后向反馈是指根据当前输出与期望输出间的误差对网络参数进行修正的过程。

训练样本经过一轮一轮的反复迭代，重复正向传播和后向反馈的过程，使得网络的预测误差不断降低。神经网络对数据特征不断进行学习训练，从而不断更新网络的权重和阈值。BP神经网络的执行流程如图2所示。

图2 BP神经网络执行流程

常用的3层BP神经网络如图3所示，所谓3层包括了输入层、隐层和输出层。

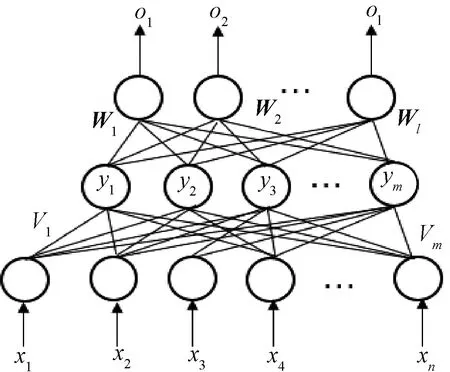
图3 3层BP网络

3层感知器中，输入向量为=(,,…，,…，)，隐层输出向量=(,,…，,…，)；输出层的输出向量为=(,,…，,…，)，期望输出向量为=(,,…，,…，)。输入层到隐层之间的权值矩阵用表示，=(,,…,,…，)；隐层到输出层之间的权值矩阵用表示，=(,,…,,…，)。

对于输出层，每个输出分量的结果与隐层输出和网络权重之间的关系为：

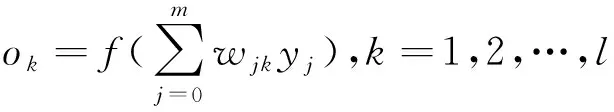
(1)

对于隐层，每个隐层输出分量的结果与网络输入和网络权重之间的关系为:

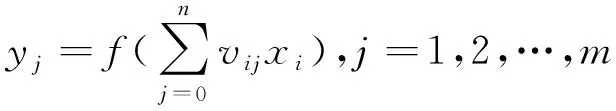
(2)

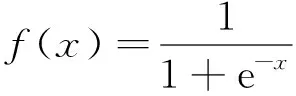
(3)

式中：转移函数()均为单极性Sigmoid函数。

在本文中，受被动侦察的限制，考虑的因素主要有辐射源的载频、重频和脉宽。而威胁等级划分为8级，因此在本实验中网络的输入节点为3，输出节点为8，中间层节点选定为7。

2.3 基于遗传算法优化BP神经网络的辐射源威胁评估算法

遗传算法优化BP神经网络，即GANN算法，是对普通BP神经网络的一种优化方法。如果把BP神经网络看成是一个预测函数，那么遗传算法优化BP神经网络相当于优化预测函数中的参数，优化后的神经网络的预测效果将明显优于未经优化的神经网络。

GANN算法分为BP神经网络结构确定、遗传算法优化和 BP神经网络预测3个部分。GANN的执行是将普通BP算法的后向反馈部分替换成遗传算法，通过遗传算法对网络的参数进行修正，利用已有数据，反复迭代正向输出和参数修正过程，直至训练出一个符合要求的GANN网络，对辐射源的威胁等级进行预测，具体的执行流程如图4所示。

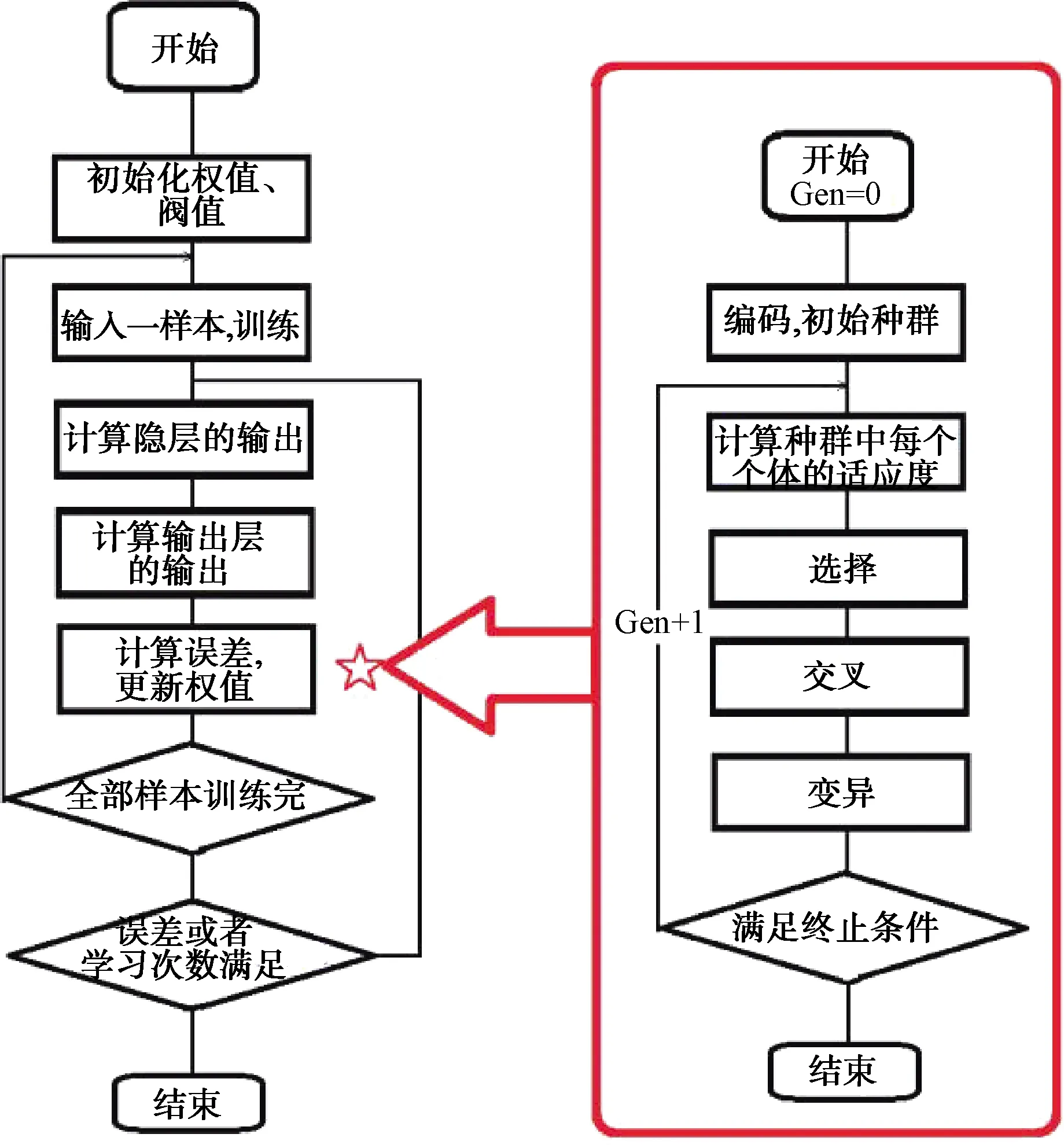
图4 GANN算法

图4所示算法流程分为两部分：左侧为神经网络部分，右侧为遗传算法部分。而遗传算法对于BP神经网络的优化，就是将原先BP的后向反馈部分替换成了遗传算法。

遗传算法优化神经网络的要素包括种群初始化、适应度计算、选择、交叉和变异的操作。GA算法部分的具体实现步骤如下：

(1) 种群初始化

个体编码方法为实数编码，每个个体均为一个实数串，由输入层与隐含层之间的权重偏置和隐含层与输出层之间的权重和偏置构成。

(2) 适应度计算

种群中的每个个体都是一组网络的权重和阈值，根据个体确定一个神经网络，用训练数据训练BP神经网络的预测系统输出，把预测值和期望值之间的绝对误差作为个体适应度。

(3) 选择操作

即个体的选择，主要基于古典概型。选择算法根据个体的适应度进行选择，适应度越小越好。在本实验中采用古典概型中的轮盘赌方法。

(4) 交差操作

根据种群个体使用的编码方法，在每个个体基因选定的节点进行交叉运算。

(5) 变异操作

对个体基因中选定的节点进行变异运算，如果采用的是二进制编码，那就将1变异为0，将0变异为1。

BP神经网络部分与普通BP网络类似，具体实现步骤简单介绍如下：

(1) 确定BP网络结构

对网络进行初始化，包括权值和阈值的初始化，再依据GA算法对权值和阈值进行编码形成初始种群个体。

(2) 构造GANN神经网络

执行GA算法部分，构造GANN神经网络，使用训练样本数据，将经BP神经网络之后得到的预测值与原始值的误差作为适应度值。经过选择、交叉、变异等操作找出最优个体，重复迭代，直到训练误差满足要求，即从GA算法部分获取经GA算法优化后的网络的权值和阈值。

(3) 预测输出

基于测试集和优化后的GANN网络，预测输出雷达辐射源的威胁等级。

3 实验结果与分析

本部分对上节中提出的基于GANN的辐射源威胁等级判决算法进行实现，并对实验结果进行对比分析。基于编程环境Python 3.8.1，使用numpy、tensorflow等框架，在Intel i5-1135G7 2.42 GHz的硬件环境下实现了GANN算法。

实验是针对辐射源的威胁等级判决问题，采用常规的BP神经网络算法和GANN算法进行求解，分别对BP神经网络算法和GANN算法在解决问题上的有效性进行验证，并对以上2种方法在解决威胁等级判决问题上所展现的收敛、搜索和预测等性能进行对比，从而得到相关结论。

实验的过程分为两部分：第一部分为BP和GANN的最优参数选取和有效性验证，第二部分为BP和GANN在辐射源威胁等级判决问题上的性能对比。本文选取了400组辐射源的脉冲描述字(PDW)数据作为样本数据。样本数据包括了机载火控雷达、搜索雷达、警戒雷达、民用气象雷达等。其中360组作为训练数据，另外40组作为测试数据。数据来源于实验采集以及相关文献。

实验一：BP算法和GANN算法的最优参数选取与有效性验证

GANN算法是在BP算法的基础上做了优化，将原先BP算法的后向反馈部分替换成了遗传算法部分，这也是2种算法的最大不同。在后向反馈部分，对算法性能影响较大的参数是学习率；在遗传算法部分，对算法性能影响较大的参数是交叉率和变异率。为规避BP、GANN算法的参数选取对实验结果产生影响，将寻找GANN的最佳交叉率、变异率以及BP的最优学习率。

神经网络的学习率指的是网络对数据学习的速率。使用神经网络对PDW数据进行学习，就是通过样本数据对网络的各权重进行迭代更新。为平衡收敛性和优化速度，采用衰减学习率。

遗传算法部分的交叉率与变异率均可自由选取，变异率不宜过高，两者均要保证在0～1之内取值，且交叉率大于变异率。一般建议交叉率在0.8左右，变异率在0.003～0.005左右。因此，选取交叉率为0.8，变异率为0.004。

遗传算法的交叉率、变异率以及BP后向反馈的学习率等参数设置完成之后，使用360组训练数据，对BP算法和GANN算法处理辐射源威胁等级判决问题的有效性进行验证，实验结果如图5、图6所示。

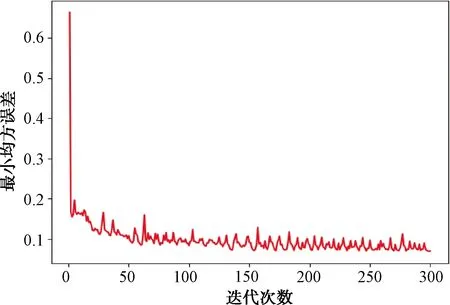
图5 BP算法收敛结果

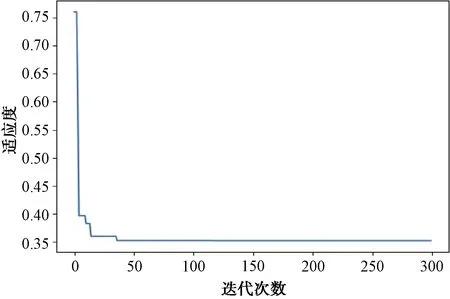
图6 GANN算法收敛结果

图5表示BP算法处理的训练数据的最小均方误差与迭代次数之间的关系；图6表示GANN算法处理的训练数据的适应度与进化代数(迭代次数)之间的关系。这里的适应度采用的就是上一部分定义的网络输出与期望输出之间的误差之和，迭代次数限制为300。

观察图5和图6可知，采用BP算法和GANN算法处理训练数据时，数据的最小均方误差和适应度均在迭代50次左右即开始收敛。其中，BP算法的最小均方误差收敛在0.1左右，GANN算法的适应度收敛在0.35左右。这说明2种算法在此问题上是可以收敛的。因此，BP神经网络算法和遗传算法优化的BP神经网络方法在辐射源威胁等级判决问题上的有效性得到验证。

实验二：BP算法和GANN算法的性能对比

(1) BP与GANN的收敛性比较

GANN算法是对于BP算法的优化与改进，GANN算法中使用遗传算法寻优替代了BP算法中的数据训练的后向反馈部分。实验一已经验证了BP算法和GANN算法可以有效收敛，现在将进一步研究对比2种算法的收敛性能优劣。

对于BP算法，使用衰减学习率；对于GANN算法，使用合理的交叉率和变异率。在此基础上，使用360组用于训练的样本数据，对2种算法处理后的数据最小均方误差与迭代次数的关系进行观察，迭代次数限制为1 000次，实验结果如图7所示。

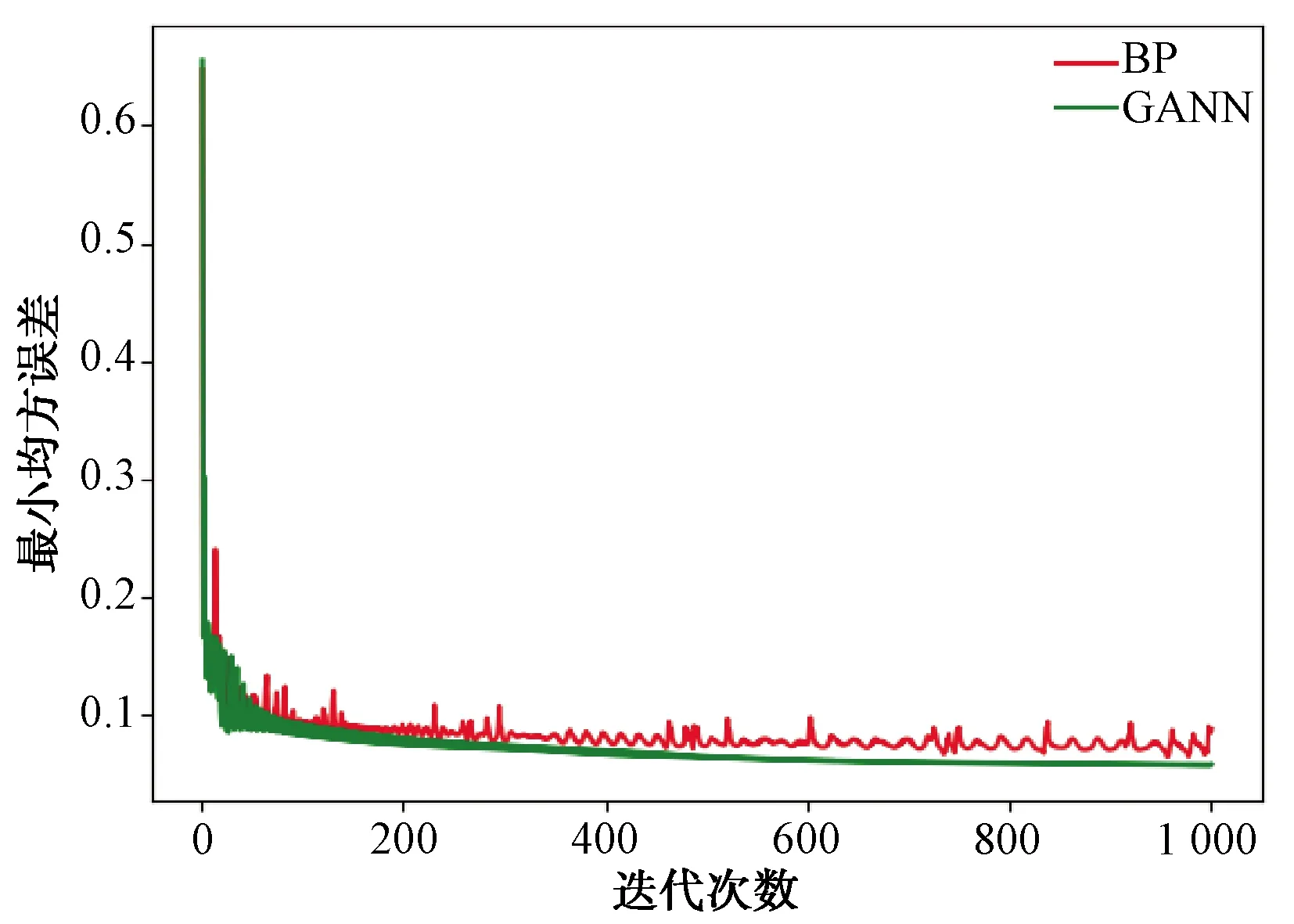
图7 GANN与BP收敛性对比

观察图7可以发现，在本实验中，GANN算法对训练数据的处理效果明显优于BP算法。这体现在2个方面：一是GANN网络的收敛速度快于BP网络，二是在1 000次迭代次数内，从200代开始，GANN算法的数据最小均方误差都低于BP算法数据的最小均方误差，且越往后差距越明显。在迭代次数为1 000时，BP的最小均方误差收敛于0.088，GANN的最小均方误差收敛于0.058。

(2) BP与GANN的搜索性能比较

为了比较BP算法和GANN算法的寻优能力，即搜索性能，不宜将迭代次数设置过大，否则不易观察微观的每次迭代的情况。将迭代次数限制为50，观察量依然为360组测试数据的最小均方误差，其他参数的设置不变，实验结果如图8所示。

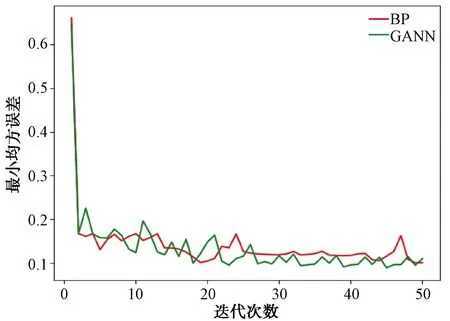
图8 GANN与BP搜索性能对比

观察图8可知，在大约第11代的时候，GANN网络已经找到了局部最优解，但它不认为这是全局最优解。于是，在网络寻优在个体变异中跳出当前的范围，在更大的范围内继续寻找，直至寻找到最优解。

前面说到，BP神经网络分为正向传播和后向反馈。后向反馈部分对权值和阈值的更新使用的是梯度下降法。梯度下降法是在单点下进行计算的，但现在计算的数据量很大，单点计算使得效率很难提高。虽然可以通过修改学习率的方式(比如衰减学习率)来控制梯度的下降，避免陷入全局最优，但是衰减学习率的方法对目标函数有很多限制。

在本问题中最终没有出现陷入局部最优的情况，但是根据实验结果以及前面的分析，可以得出结论：GANN算法具有比BP算法更优的全局寻优能力。

(3) BP与GANN的预测效果比较

基于前面确定的合理的算法参数设定以及360组训练样本数据，使用BP算法和GANN算法分别训练出了1个辐射源威胁等级预测模型，即训练得到了神经网络的各个权值和阈值的最终数值，并使用此神经网络进行数据预测。

采用训练好BP神经网络和GANN神经网络对辐射源威胁等级进行测试，测试数据为40组，实验结果如图9所示。

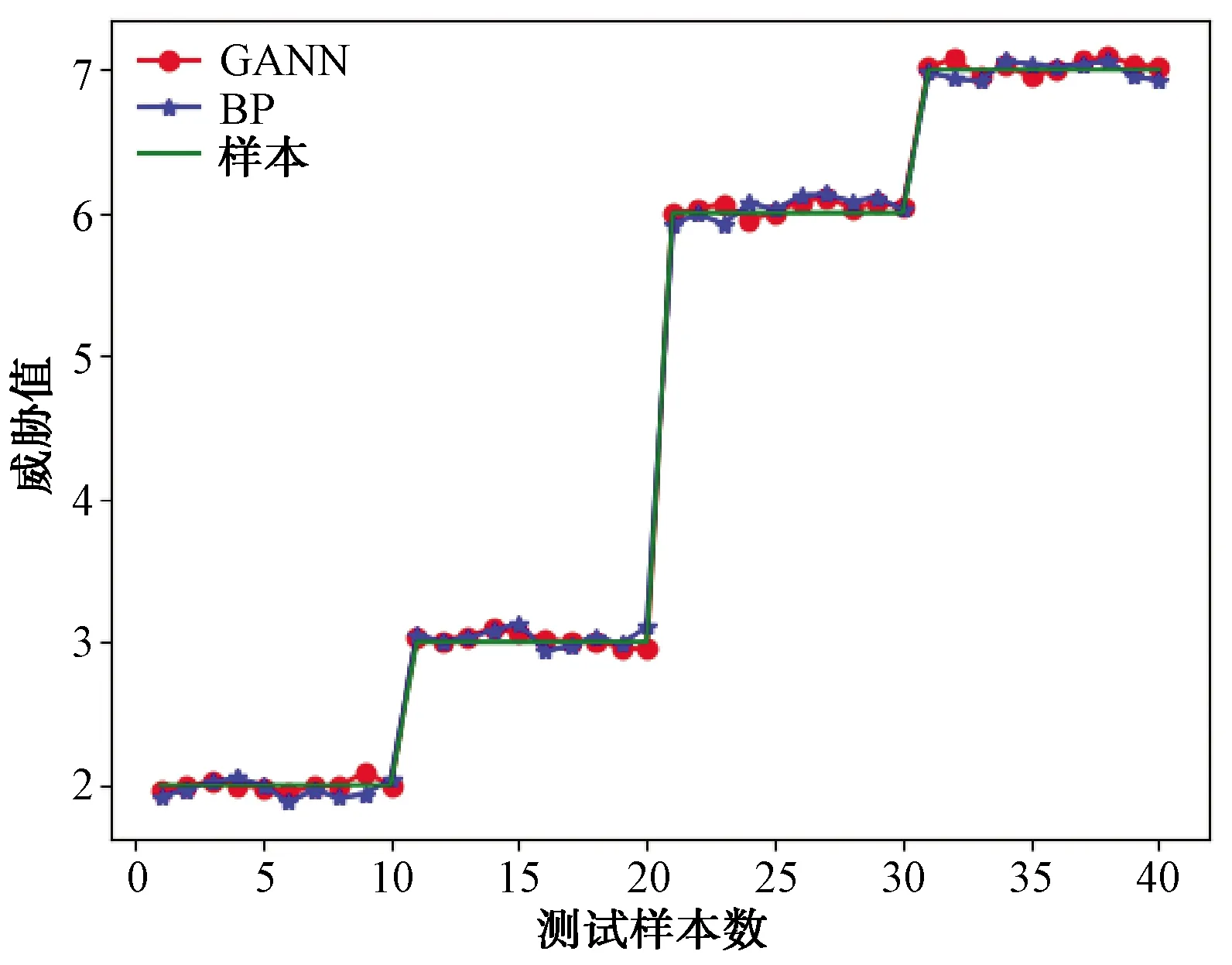
图9 实际威胁值与预测威胁值

图9表示的是BP网络的预测值、GANN网络的预测值与实际的40组测试样本数据值之间的比较。40组测试样本分别选用了10组跟踪雷达PDW，10组机载火控雷达的PDW，10组搜索雷达的PDW，10组民用气象雷达的PDW。威胁等级分别为2，3，6，7。为了便于观察，计算出BP的预测值与实际值之间的误差、GANN的预测值与实际值之间的误差，并将二者进行比较，如图10所示。

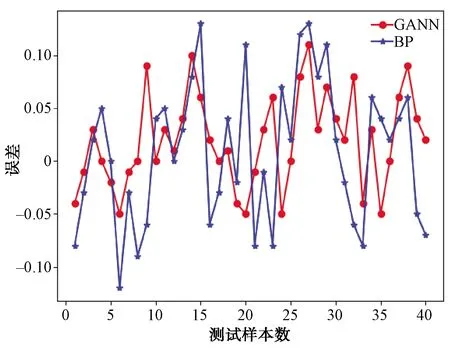
图10 GANN与BP的预测误差

观察图10可以看出，GANN的预测值更接近于真实值，其误差明显小于BP的预测值。

4 结束语

本文针对认知电子战中辐射源的威胁等级判定问题，提出了GANN新型学习方法。新型算法在训练数据时将BP神经网络原先的后向反馈操作替换为遗传算法的遗传进化操作。以此算法为基础进行实验，对优化后的算法和普通的BP算法的性能进行比较。实验结果表明，新型算法GANN在收敛、搜索和预测性能上均优于BP算法。因此可以得出结论：在处理辐射源威胁等级判决问题上，使用遗传算法优化后的神经网络算法GANN比传统的BP神经网络算法更具优势。