高层建筑抗风优化设计和风振控制相关问题研究

傅继阳，吴玖荣，徐 安

(广州大学风工程与工程振动研究中心，广东，广州 510006)

1 高层建筑抗风优化设计研究

结构优化理论从20 世纪50 年代提出以来，得到学术界和工程设计领域的广泛重视，并成功应用于汽车制造、航空航天等众多领域。但在高层建筑结构设计领域，可用于结构抗风设计方法的研究还为数不多。随着高层建筑朝着高耸化和新颖化方向的飞速发展，目前世界上最高的迪拜塔已达到了828 m。随着结构高度的增加，风对高层建筑的影响也在加大，对于超高层建筑，风荷载已经成为结构设计的主要水平控制荷载。

高层建筑结构优化的主要目的是使结构在满足结构性能设计要求的前提下，通过优化设计手段，达到降低成本、改善结构设计的目的。针对这一目的，香港科技大学Chan 等[1-8]较早进行等效静力风荷载作用下高层建筑的抗风优化研究，并建立了一套优化设计方法，其主要优化算法是采用最优准则法(OC 法)，并以构件截面尺寸为设计变量，以风致顶部位移、层间位移和结构自振频率等为约束条件，以工程造价或结构总重为优化目标，实现优化目标函数的最小化[5,8]。利用虚功原理、瑞利商原理及功能转换关系，Chan 等[4-5]建立了位移、层间位移和自振频率的显式表达式，通过建立风致加速度响应的显式表达式，并将其转化为频率约束，从而建立了在抗风优化中考虑舒适度约束的有效方法[6,8]。在此基础上，认为优化过程中结构构件尺寸的改变将会引起结构动力参数的改变，从而对作用于结构上的等效静力风荷载产生一定程度的影响[1]。Huang 等[9-12]在Chan 研究的基础上，进一步开展了相关研究工作，通过一个高层建筑结构标准模型CAARC (Commonwealth advisory aeronautical research council)的算例进行自振频率约束的优化设计方法研究。傅继阳等[13-18]利用最优准则法(OC法)对高层建筑考虑风速风向联合分布以及基于性能化的抗风设计也进行了相关的研究工作。Spence 等[19-21]也将可靠度理论应用于抗风优化设计，对大型结构在随机风荷载下进行荷载和响应的概率性优化设计，其核心思想是通过一系列高精度的相似理论将可靠度和概率分析迭代过程从优化循环迭代过程中解耦出来，既实现了在优化中考虑变量随机性的问题，又简化了计算过程，并通过实例验证了该方法的实用性，Petrini 等[22]也在抗风设计方面开展了相关的研究。总体而言，高层建筑结构的抗风优化设计研究目前开展的还比较少，尤其中国对这方面的研究更少，在风振响应和等效静力风荷载的计算上还有改善的必要和空间，对外部风荷载随机性和概率性的考虑和其可操性的研究还比较缺乏，有必要对结构抗风优化的方法进行进一步的探索。

约束条件是高层抗风优化设计中非常重要的因素，从现有的研究文献来看，针对高层建筑的结构特点，结构风致位移[9,21]和加速度响应[8]是主要的控制要点，经常作为约束条件使用，其中位移约束包含位移(一般是楼顶位移)和层间位移，加速度响应常被等效为频率约束[12]，而且这几种约束条件往往结合起来一起参与优化设计。

抗风优化设计中另一个重要因素是优化算法的选择，OC 法(最优准则法)由于理论比较成熟，收敛性好，应用比较广泛，是目前高层结构优化设计的主要算法[2,8,20-21]。特别是对于高层结构优化设计，变量数目相对于约束条件数目要大得多的特点，OC 法由于优化运算收敛性快、优化运算工作量小，因而在高层结构优化设计中仍然是主流算法。Moharrami[23]对OC 法的发展状况进行了详细的梳理，并对基于库恩-塔克(Kuhn-Tucker)最优条件的OC 法和运用二次规划法求解拉格朗日乘子的过程进行了详尽的推导与讨论。因此，本文在进行基于截面尺寸的高层建筑抗风优化设计中，选择位移、加速度或频率作为约束条件，并主要选用较为成熟的OC 法作为优化算法。

OC 法是目前高层建筑抗风优化设计选用的主要算法，但该类算法需要针对不同类型的目标函数、约束条件等导出不同的优化准则，且一般要在优化过程中对目标函数、约束函数对设计变量的敏感度进行分析(即可具有可导或可微要求)。上述要求对于一般的结构抗风优化问题不一定都可以满足，此时可采用基因遗传算法、神经网络算法、粒子群算法等无需对目标函数、约束函数求导的智能优化算法。基因遗传算法核心思想是算法的优化和搜索过程模拟生物体进化过程，每个搜索空间上的点作为一个个体，目标函数值作为个体对环境的适应能力，通过优胜劣汰产生下一代更优秀的种群，迭代至满足设定的条件为止。计算机技术的发展为该算法应用提供了硬件支撑，目前已有大批学者投身于基因遗传算法的研究当中。Koza 等[24]系统阐述了基因遗传算法的方法与理论；Tsahalis 等[25]提出了多目标优化方法；黄炎等[26]提出基于可调变异算子解决遗传算法欺骗性问题的方法，在保证种群多样性同时，使算法向全局最优解收敛；曾国荪等[27]分析了并行遗传算法的动机及模型；目前遗传算法已应用于自动控制[28]、工程设计[29]、资源调度等领域。遗传算法具有强鲁棒性、无需敏度分析、可处理线性和非线性问题等特点，具有较广的应用面。

基因遗传智能优化算法的主要特点是具有较强的通用性和全局寻优能力，并且容易开发成通用性抗风优化设计软件用于工程实践，但是其耗时长，对计算设备和运行软件依赖性较高，是伴随着计算机的进步而发展起来的算法。传统基因遗传算法中存在以下3 个问题：① 决定GA 的搜索速度与效率的交叉运算得出的结果由初始种群个体分布决定，能提高全局搜索能力的变异算子的变异结果受初始种群个体分布影响，遗传算法的全局收敛性能、收敛速度受初始种群个体分布情况影响较大，而传统的基因遗传算法的初始种群是随机产生的；② 大量模式相当的个体集中在平均适应度附近，延缓收敛速度；③ 处理约束时，传统的基因遗传算法采用固定的罚因子，不利于扩大搜索范围，易导致进化后期最优解落于不可行域。因此对传统基因遗传算法进行改造，引入初始种群多样性评价函数改善初始种群质量，改进自适应遗传算法，引入动态罚函数模型和分级遗传算法，是提高此类智能优化算法收敛速度和尽快获得最可能优化解的重要途径。

基于OC 法和基因遗传算法的尺寸优化(Size optimization)算法，是在满足约束条件下，在给定结构形状基础上，求杆件截面面积最小或板单元优化厚度的常用方法。通常指在设计域中已确定节点和杆件的连接位置，在这种方法中，设计域、形状或杆件连接方式不会更改。而拓扑优化(Topology optimization)克服了尺寸优化存在的限制，它通过改变材料的位置和结构的形状，更能代表一个结构优化后的结果。拓扑优化是在给定的边界条件和荷载条件下，对将要建造的结构的体积，以及可能的一些附加设计限制。通过在设计域内保留和删除设计材料，以便得到最优拓扑布置的数学优化过程。优化结果可以是任何的形状、尺寸和拓扑关系。

随着国内外学者的不断深入研究，对拓扑优化方法的研究不断深化。特别是Guedes 和Kikuchi[30]提出了均匀化方法，拓扑优化已变得更加先进和广泛使用。后来Bendsøe 等[31]在均匀化方法基础上发展了变密度法。变密度法基本目标是，通过确定每个单元是由固体材料还是由空隙组成来最小化目标函数。通过选择合适的插值函数，将连续的密度变量与材料的物理属性连接起来，然后通过惩罚因子使得中间的密度变量向两边靠拢。在此基础上Bendsøe 等[32]和Rozvany 等[33]提出了基于各向同性材料假定的惩罚模型，即SIMP(Solid isotropic material with penalization)插值理论，变密度法的简单性使得其在工业界和学术界得到广泛使用和接受。但是，变密度法在求解过程中可能会出现数值不稳定现象，如出现棋盘效应、网格依赖现象，这时候可以通过使用过滤技术或者添加约束来处理这些不利影响。为此，为了提高计算变密度法拓扑优化设计的效率，本文引入分层优化的概念，同时采用OC、MMA 和FMINCON 内点法作为优化算法进行拓扑优化计算，以比较三种变密度拓扑优化求解算法的收敛性快慢程度。

作为拓扑优化中的另一种常用优化算法—渐进结构优化法，为Xie 和Steven[34]在1993 年提出。由于进化方法具有相对简单的理论基础和便利的应用价值，它已成为拓扑优化领域的一个热点，受到国内外学者的广泛关注和研究。其发展的第一阶段主要是Xie 和Steven 等[35]对早期ESO方法的研究。1997 年，Xie 和Steven[36]出版了第一本关于渐进结构优化法的专著《Evolutionary Structural Optimization》(《渐进结构优化》)。但早期ESO 法存在如下的缺点：在优化初期，某些单元由于灵敏度较低被删除，优化后期这些单元可能会变得越来越重要，但是ESO 法无法把删除的单元进行恢复，所以在大多数情况下，ESO 法可以获得较优解，但未必是最优解。为进一步完善早期的ESO 法，以1999 年Yang 和Querin[37-38]提出的双向渐进结构优化法(Bi-directional evolutionary structure optimization，BESO)为分界点，关于ESO 法的研究进入第二个阶段—BESO法。BESO 法的主要原理是，既删除低效单元，同时也在高效区域周围添加单元，这大大补充完善了ESO 方法的不足之处。

在双向渐进结构优化方法中，单元删除准则和增加准则是至关重要的参数，不同的该两项参数将会产生不一样的拓扑优化结果。一般而言，初始删除率和进化率越小，优化结果就越准确，但是运算时间大幅增加、计算效率低；初始删除率和进化率越大，计算效率就大大增大，但有时会因为误删单元而导致最终优化结果出错，得不到最优解。为此，本文对BESO 法进行局部改进，提出一种动态自更新进化率的双向渐进结构优化方法，以获得更优的拓扑优化结果。

2 高层建筑风振控制研究

高层建筑、高耸结构具有高宽比大、细柔而轻质等特点，对于此类风敏感性建筑，风荷载往往成为其结构设计的控制性荷载。因此为使高层建筑和高耸结构做到安全、适用、经济、美观等要求，对其进行结构风振控制是十分必要的。结构振动控制是将振动控制系统安装到被控结构上，被控结构在地震或风荷载作用下，主体结构与控制系统共同运动，控制系统对主体结构产生控制反力，以减少主体结构的动力响应，实现控制的目的。振动控制系统的分类，按照控制系统能量的输入分类，可分为主动控制、半主动控制、被动控制等几类[39]。由于被动控制的控制原理简单，在实际发挥作用时无需从外部输入能量，因而在实际工程中得到了广泛的应用。被动控制可分为：基础隔震、耗能减振和调谐质量阻尼器等几类[39]。

其中，基础隔震装置中的摩擦摆装置(Friction pendulum system, FPS)1985 年由Zayas 等[40]在加州大学伯克利分校提出；Tsopelas 等[41]首次将FPS 系统运用于桥梁的隔震；Constantinou 等[42]对双向FPS 摩擦摆系统进行了系统的理论研究。王肇民、欧进萍、张相庭等[43-46]专家学者对TMD系统风振控制的相关理论、计算方法、参数计算以及风洞试验进行了深入细致的研究，得出TMD系统控制的相关设计分析方法和TMD 风振控制优化设计方法。李春祥等[47-48]对高层建筑带TMD控制系统优化设计进行了深入研究，分别得到在风荷载作用下的最佳控制参数和地震基频对TMD最优动力特性的影响。

本文将被动控制中的基础隔震与调谐质量阻尼器结合，组合成一种新颖的被动控制装置，即摩擦摆调谐质量阻尼器系统(Friction pendulum system tuned mass damper, FPS-TMD)，对其作用机理与在风荷载作用下的控制效果进行研究[49-50]。同时将FPS-TMD 系统作为实验子结构，主体结构作为数值子结构，利用小型电振动台进行风振控制实时混合实验，通过实时混合实验的方法，验证本文前期所提出的FPS-TMD 系统作用机理，以及顶部带FPS-TMD 装置高层建筑的风致振动效率的理论分析结果。

3 高层建筑抗风优化设计

3.1 基于最优准则法和可靠度理论考虑风速风向联合分布的高层建筑抗风优化设计

本小节针对高层建筑对风荷载的敏感性、风荷载本身的复杂性，从概率的角度应用可靠度分析方法，充分考虑风速风向联合分布的影响，以风工程领域广泛应用的CAARC 标准模型为优化对象，采用OC 法(Optimality criteria，最优准则法)为优化算法，以结构构件总质量为目标函数，并主要以结构顶部水平位移、各层层间位移和结构自振频率为约束条件。

为了考虑风向的影响和确定合理的设计风荷载，建立了风速大小分布及方向分布的概率模型。同时，从可靠度的角度，以条件概率的形式，将加速度限值代入得到每个风向的可靠度方程。然后，根据各风向频率计算考虑多风向的失效概率。联立所有风向对应的可靠度方程和失效概率方程，求得满足所有方向可靠度指标和加速度限值的结构自振频率最低限值，并将其应用于优化设计[51-54]。

位移和层间位移是结构设计中的主要控制目标。整体结构的风致位移和层间位移，则在应用随机振动理论进行整体结构的等效静力风荷载计算的基础上，通过静力方法来进行优化求解。

1) 优化对象

CAARC 模型是结构风工程领域广泛应用的一个高层建筑标准模型，其长宽高三个方向的尺寸分别为45.72 m×30.48 m×182.88 m，如图1 所示。

图1 CAARC 标准模型 /mFig. 1 CAARC model

标准模型的结构类型假设为钢筋混凝土框架结构，结构构件初始截面信息如表1 所示，混凝土强度为40 层以下是C80，40 层以上是C60。

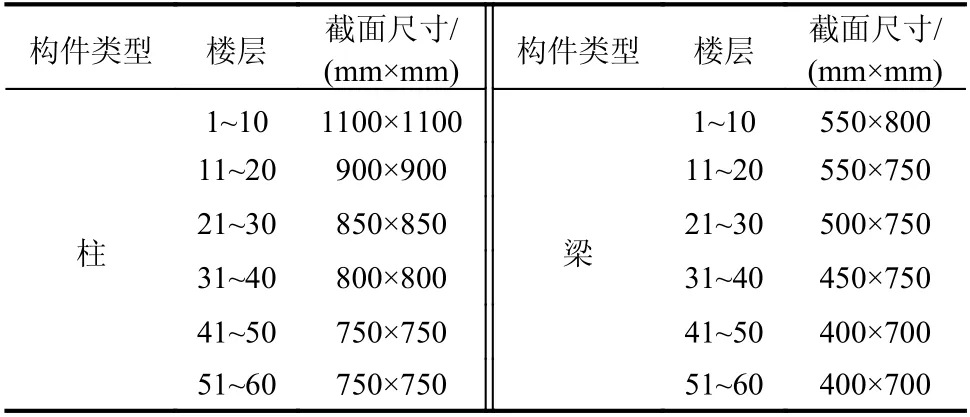
表1 标准模型中结构构件初始截面尺寸Table 1 The initial section sizes of structural members in CAARC model

2) 优化设计模型

下面根据前面定义的设计变量、目标函数和约束条件，建立结构截面尺寸优化的数学模型。

设计变量：

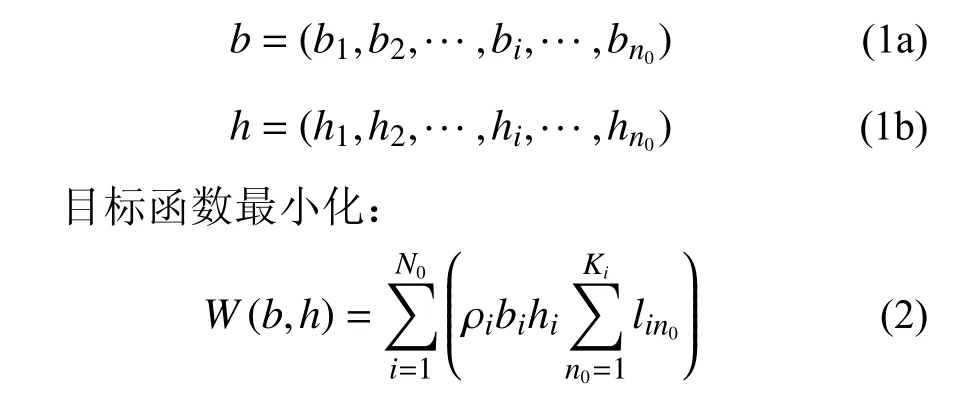
满足约束条件：

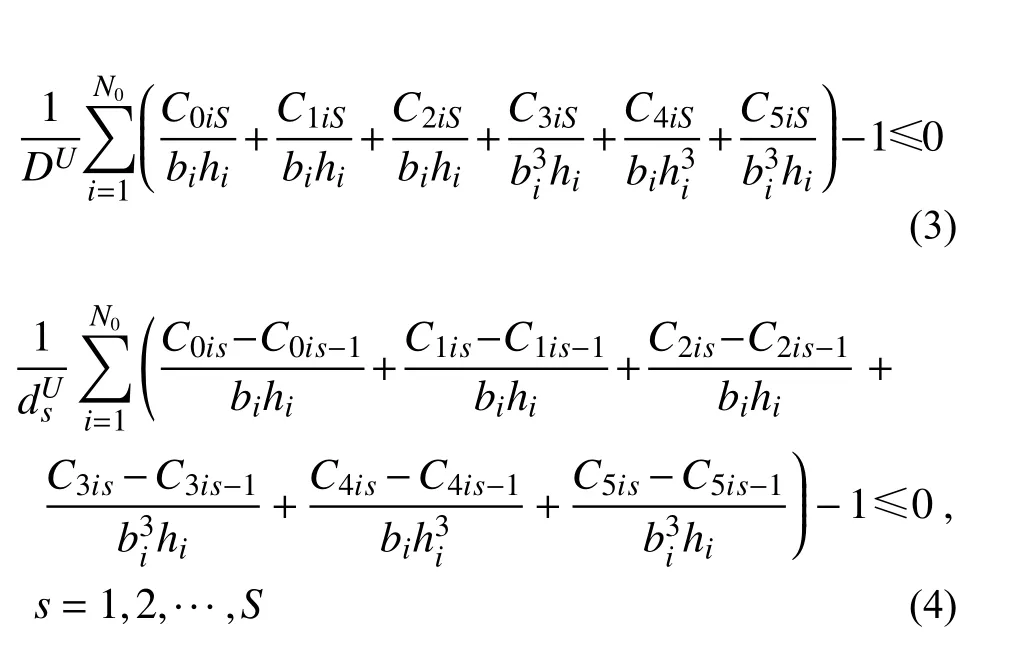
其中：层间位移约束条件可以将所有楼层作为约束条件，也可以选择部分楼层作为约束；结构顶部位移和层间位移约束表达式的系数，通过在求得整体结构等效静力风荷载的基础上，通过虚功原理来获得。风致加速度约束(对应的频率约束)一般取建筑主轴两个方向的第一阶自振频率作为约束条件。频率约束表达式的约束系数，对于确定性约束条件，可以根据虚功原理结合瑞利商的原理来获得。

当考虑最不利单风向且基于可靠度的风致加速度约束(对应的频率约束)时，根据结构设计规范对加速度响应的限值要求，建立如下的可靠度问题。

可靠度极限状态方程和失效概率如下：

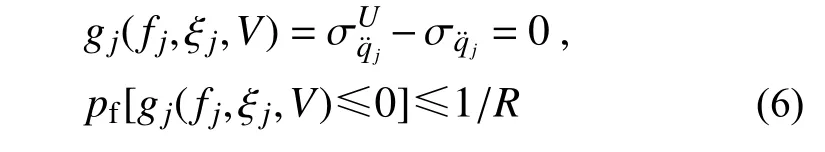
根据随机振动理论，可以建立结构加速度响应与结构自振频率及所受风荷载等参数的显式表达式，并将式(5a)中的结构基阶自振频率、阻尼比和风速以随机变量来考虑。将加速度的计算表达式转化为由3 类服从一定分布的随机变量(频率、阻尼比和风速)组成的关系式，并假设阻尼比和风速的统计特征已知的基础上，采用可靠度理论中的当量正态化方法，将非正态随机变量变换为正态随机变量，再利用验算点法将风致加速度响应限值的可靠度约束条件，转化为结构自振频率限值的确定性约束条件。

当考虑多风向条件下的风速风向联合概率分布且基于可靠度的风致加速度约束(对应的频率约束)时，根据结构设计规范对加速度响应的限值要求，建立如下的可靠度约束方程组。

可靠度方程和失效概率如下：

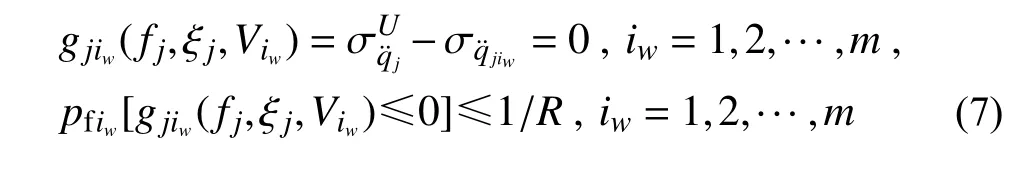
式中，R为基本风压的重现期。根据计算舒适度所采用的基本风压的重现期R(中国规范为10 年，本文采用10 年重现期基本风压计算加速度响应)，可以反算与规范对应的加速度响应的年失效概率最高限值(1/R)，于是式(9)成为包含m个未知数(各风向下对应的可靠度指标)的方程，其中离散的风向分布函数A(θiw)由气象观测所得(如图2 所示)。这个方程便将多个风向下独立的可靠度方程结合起来，并组成包含m+1 个未知数和m+1 个方程的非线性联立方程组：

图2 广州市番禺气象站年风向玫瑰图Fig. 2 The wind rose graph of wind direction for Panyu Station in Guangzhou

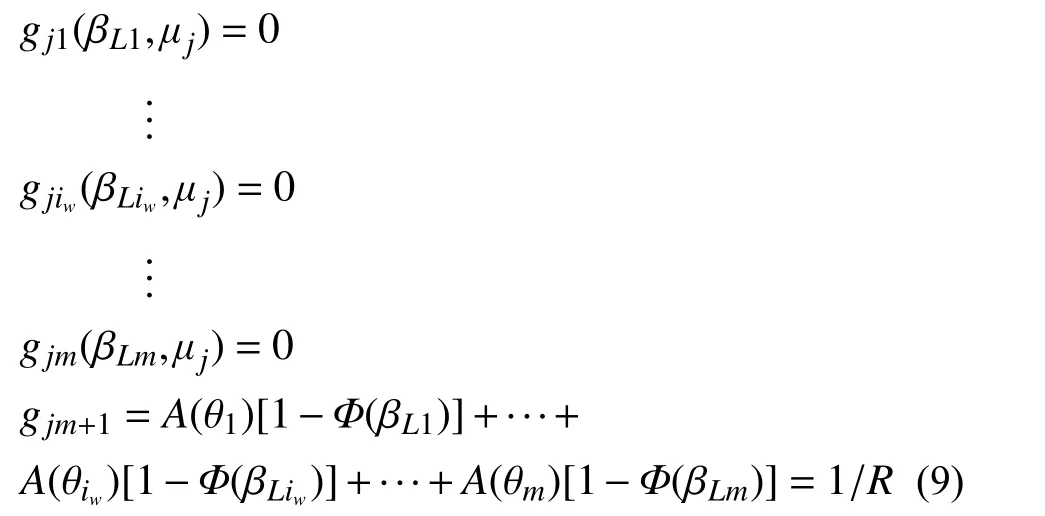
结构优化设计算法采用比较成熟的最优准则法(简称OC 法)。OC 法迭代次数少、收敛快，特别适用于设计变量较多的大型复杂结构，在结构优化设计领域得到广泛的应用。

3) 气象参数

为在抗风优化设计中更加真实地反映风荷载信息，在建立频率约束时充分考虑风速的随机性，本章引用广州市番禺气象站的常年气象观测资料[55]作为优化设计中的风荷载参数，各风向下风速基本服从Gumbel 分布(表2)。

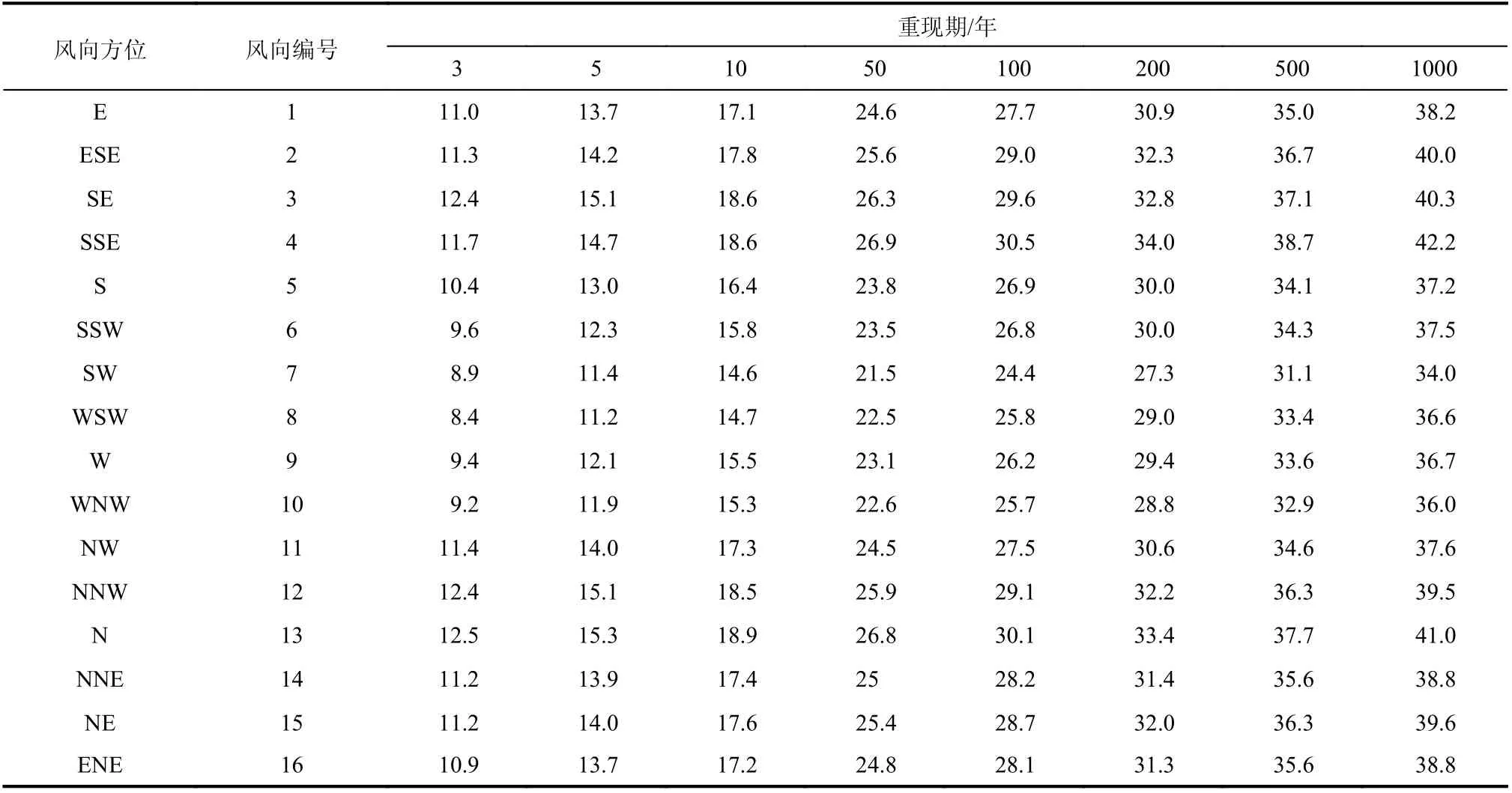
表2 Gumbel 分布计算各重现期下的对应风速[55]/(m/s)Table 2 Estimated wind speed with different return periods

4) 单风向下基于可靠度频率约束的抗风优化设计

根据计算和讨论可知，对于位移和层间位移响应，5 号(90°)和13 号(270°)风向为最不利风向，对于加速度响应，1 号(0°)风向为主轴X向第一阶加速度响应的最不利风向，13 号(270°)风向为主轴Y向第一阶加速度响应的最不利风向。在结构优化设计中分别以此作为最不利风向进行优化设计。

表3 和表4 说明对于考虑风速、频率和阻尼比的随机性与否，对优化结果是有影响的，可以在考虑频率约束的前提下，进一步提高优化空间，而且这样考虑更加符合结构的实际情况。

表3 结构优化设计工况统计表Table 3 Statistics results of structural optimization design

表4 结构优化设计历程中各工况下结构构件总重/tTable 4 Variations in the total weight of structural members under various loading cases during the structural optimization design

5) 基于可靠度和风速风向联合分布考虑结构风致舒适度的高层抗风优化

根据计算结果，对考虑第一阶模态的加速度响应的可靠度计算，分别选择4 个(风向编号1、2、9、16)和6 个(风向编号1、2、4、9、13、16)较不利风向。

考虑多个风向时的风速风向联合分布和可靠度的结构构件总重优化结果如图3 所示。在4 个风向和6 个风向工况下，结构构件总重都呈下降趋势，两者最终的收敛值几乎完全相等，相较于优化前的构件总重降低了44.34%，说明从目标函数的优化结果来看本次优化取得了较为显著的效果。

图3 结构构件总重优化结果Fig. 3 Optimization results for the total weight of structural members

在各工况下，前二阶频率在优化过程中的变化情况如表5 所示。在表中可以比较清晰地观察到，X向第一阶和Y向第一阶自振频率在4 个风向和6 个风向工况对应的频率限值差别较大，尤其是第一阶频率限值，差别达到26.05%，可见参与风速风向联合概率分布的风向的个数及方位对优化结果的影响是较大的，进一步说明了风向的重要影响。

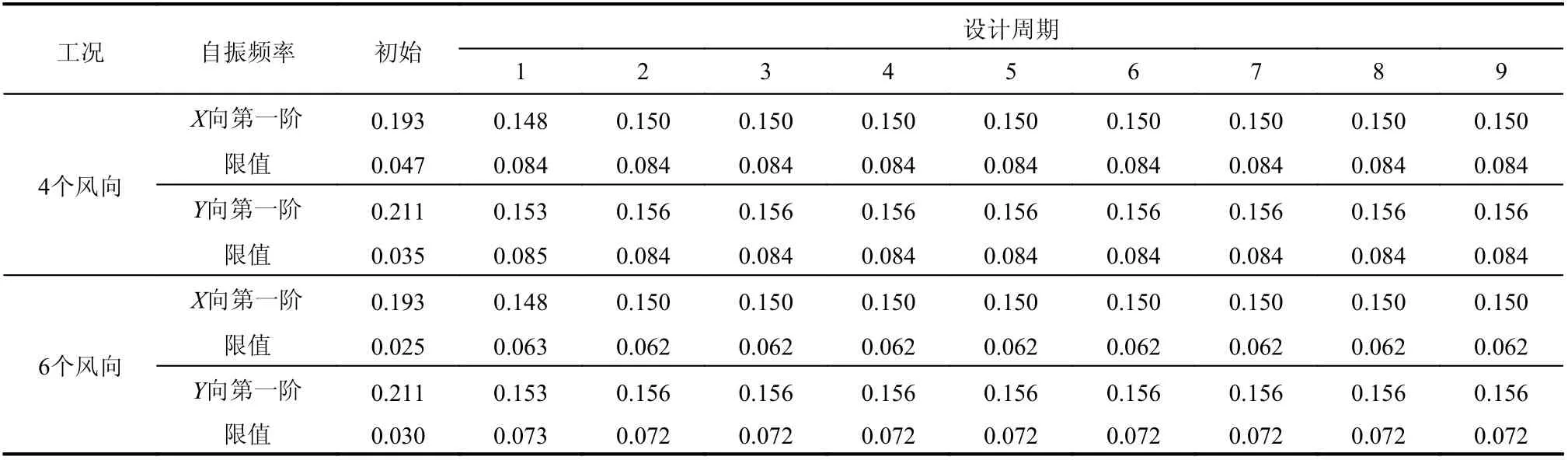
表5 结构优化设计历程中各工况下结构前二阶频率及限值/HzTable 5 The natural frequencies for the first two vibration modes and the corresponding limit values under various loading cases during the structural optimization design

从上述优化结果证明，考虑风速风向联合分布可以提高优化空间，在满足所有约束条件的情况下，目标函数低于单风向下的优化结果，说明了考虑风速风向联合概率分布的必要性和意义。

在基于上述算法的基础上，可进一步考虑基于性能的高层建筑抗风优化设计，其详细算法可参见文献[14]。

3.2 基于有限元动力分析中特征值求解的自振频率约束优化

频率约束为高层建筑风致舒适度抗风优化设计所必须考虑的主要因素，在采用最优准则法对结构进行自振频率约束的结构优化方法中，传统应用较多的是采用应变能法进行等价处理，但其约束函数对设计变量的敏感度是假定结构内力向量不随结构优化设计变量(一般为截面尺寸)而改变，这样不精确的约束函数敏感度值代入结构优化迭代计算，容易带来误差累积而使结构优化结果不是最优解。本文从求解高层建筑结构模型自振频率的特征值法的公式入手，推导求解结构频率约束对优化设计变量敏感度的精确公式；通过一个高层建筑结构标准模型CAARC (commonwealth advisory aeronautical research council)的算例进行自振频率约束的优化设计方法研究。

1) 结构特征值灵敏度公式推导

式中：K、M为结构整体刚度、质量矩阵；{φ}k为第k阶振型。式(10)关于结构尺寸变量Xi偏微分，可得：

式中：Nε为与节点ε 相连接的单元数；ρ、V为空间梁单元的密度和体积。对于空间梁单元j，其质量mj对截面尺寸Xi的偏导有：

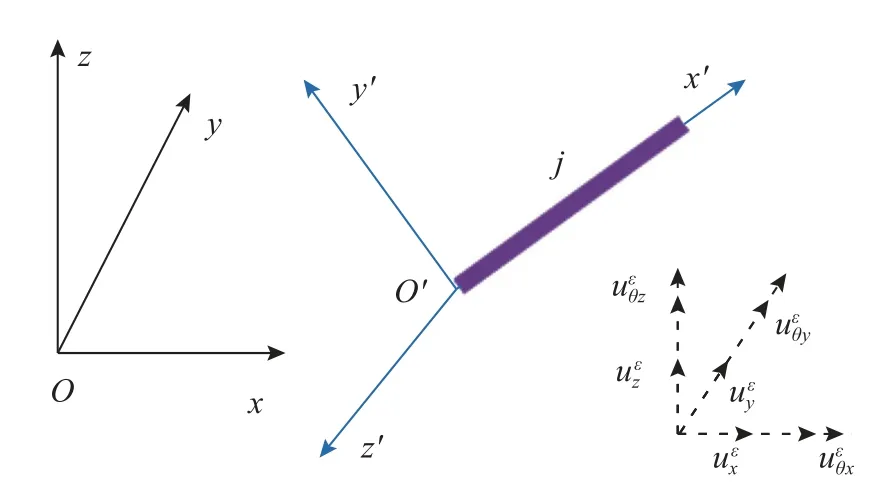
图4 空间梁单元局部坐标系与整体坐标系Fig. 4 Local and global coordinate systems of spatial beam element

本文以高层建筑结构标准模型的三维SAP2000 有限元模型(如图1(a)所示)为例，其结构类型为钢筋混凝土框架结构，层高3.048 m，共计60 层。框架梁与柱都采用矩形截面，并且每隔10 层分别作为一类结构设计构件，因此整体结构总共有12 个截面设计变量。框架梁与柱构件材料为钢筋混凝土，混凝土强度等级40 层以下为C80，40 层以上为C60。沿建筑结构高度方向，每层设置刚性隔板，且在楼层形心处设置点单元并附加质量，顶层主节点三个方向的附加质量为mux=muy=603.1183 t，muθz=102 020.22 t·m2，其他楼层处主节点三个方向的附加质量分别为mux=muy=765.6358 t，muθz=152 635.08 t·m2。

对高层建筑标准模型CAARC 进行结构基振频率约束的优化设计，取fL=0.1522 Hz。表6 给出了结构构件初始截面以及最终优化迭代设计结果等相关信息，图5 与图6 给出了采用应变能法与特征值法的各参数指标的迭代结果，可以发现：① 两种方法计算的结构基振频率、总重、构件截面尺寸等指标都得到了收敛，结构基振频率收敛于约束限值；② 构件总重采用特征值法最终收敛于20 796 t，采用应变能法收敛于20 800 t，二者相差0.019%；③ 从OC 迭代的次数上看，由于采用特征值法的约束函数敏感度值较应变能法更精确，特征值法只需较少的OC 迭代步优化结果就可收敛，说明特征值法迭代效率优于应变能法。

图5 应变能法迭代结果Fig. 5 Optimization results by strain energy method

图6 动力分析特征值法迭代结Fig. 6 Optimization results by eigenvalue method

表6 标准模型中结构构件原始截面信息及迭代结果Table 6 Initial member size and optimized results of structural members in CAARC model

3.3 基于基因遗传智能优化算法的高层和高耸结构抗风优化设计

1) 基于改进罚函数及分级遗传算法的结构优化设计

遗传算法的研究越来越受到人们的关注，其在解决优化问题时无需将约束条件显式表达，可以方便地处理各类工程结构优化问题中的位移、频率以及应力约束问题，因此在结构优化设计的应用中优势明显。但研究人员已注意到基本遗传算法存在一些不足之处：① 容易出现过早收敛，难以得到全局最优解；② 不能将优化问题的约束表示出来；③ 搜索效率低；④ 局部搜索能力差。为了改善基本遗传算法的这些缺陷，笔者从约束条件的处理、改进罚函数、分级排序、选择算子和交叉变异方法等多个方面对遗传算法进行了改进。新的方法可以较好地实现种群的双向进化，提高算法的性能，尤其是对于需要消耗巨量的时间来进行有限元分析的工程结构优化问题是显著的。

为了测试本文所提出的改进罚函数分级遗传算法，分别将其应用在两个经典的求最值数函数中。

① De Jong 函数是一个连续、突起的单峰函数，其表达式如下所示：

这里，n为优化问题的维度，本案例设n= 20，求解minf(x)。图7 为De Jong 二维函数图形，图8为改进算法的目标值迭代图。

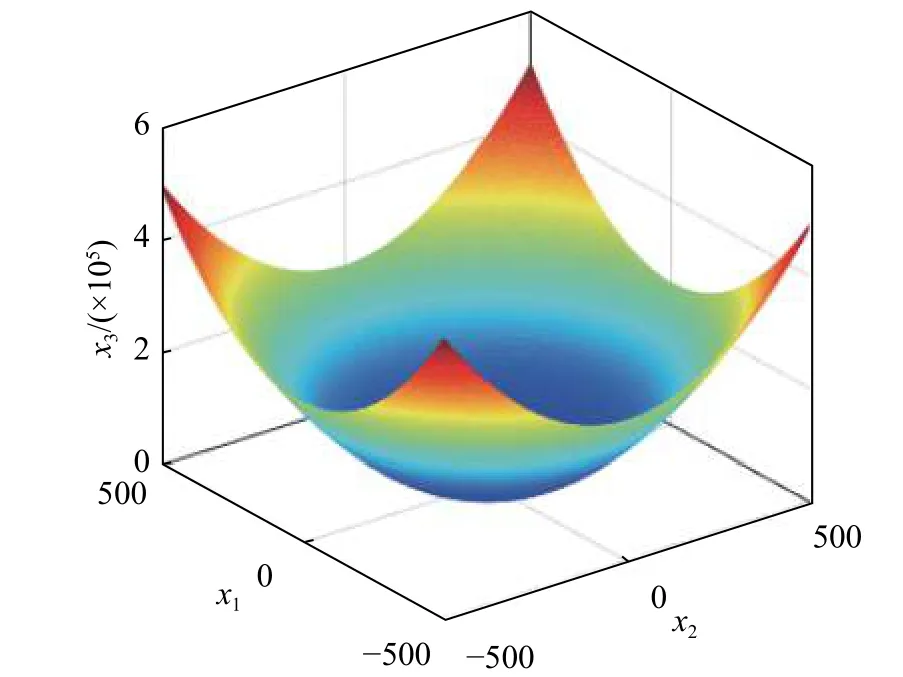
图7 De Jong 二维函数图形Fig. 7 Diagram of De Jong in two diemsional function

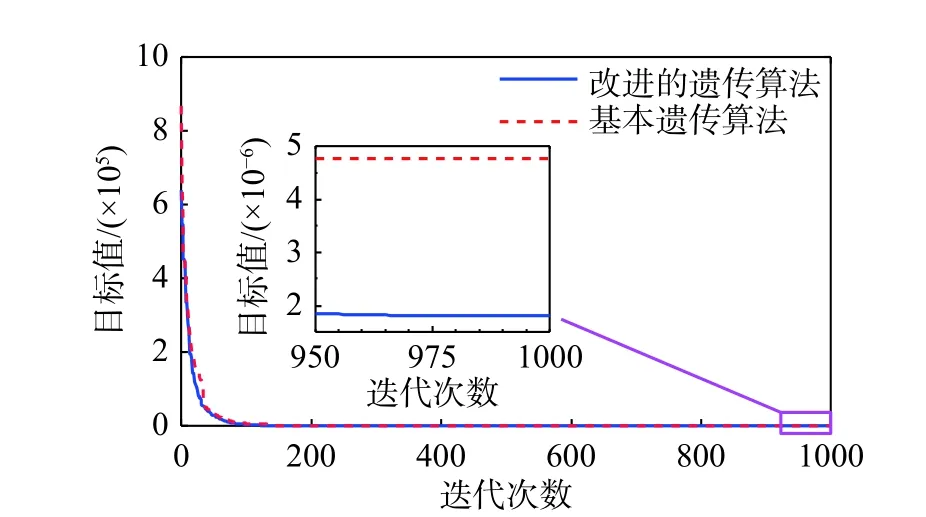
图8 目标值迭代图Fig. 8 Target value after several iteration

② Shubert 函数为多峰函数，其二维变量表达式如下所示：

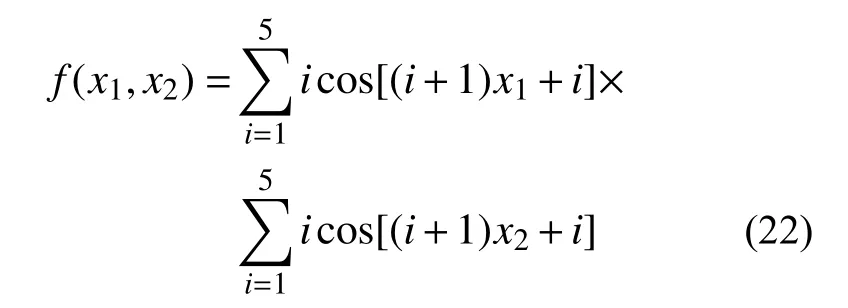
图9 为Shubert 二维函数图形，图10 为改进算法的目标值迭代图。2) 优化算例—CAARC 标模抗风优化设计

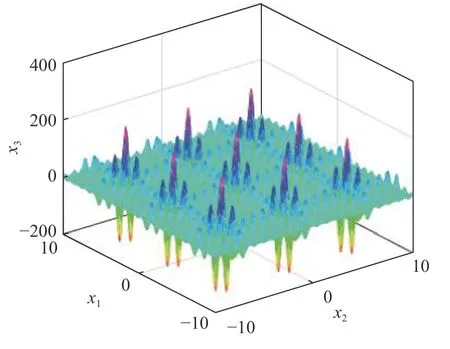
图9 Shubert 二维函数图形Fig. 9 Diagram of Shubert's 2D function

图10 目标值迭代图Fig. 10 Target value after several iterations

该结构几何尺寸为45.72 m×30.48 m×182.88 m，整体形状为矩形柱体。优化数学模型如下：

结构模型如图11 所示，最终优化结果如图12所示。

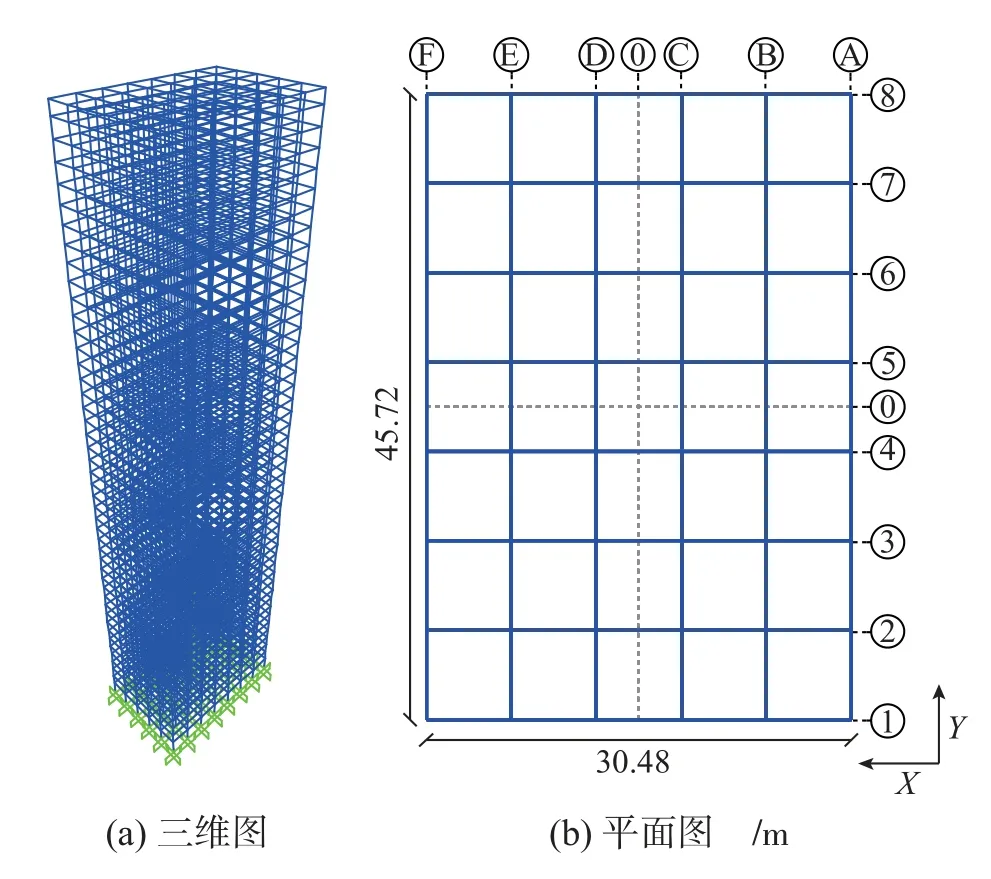
图11 结构模型Fig. 11 Structural model

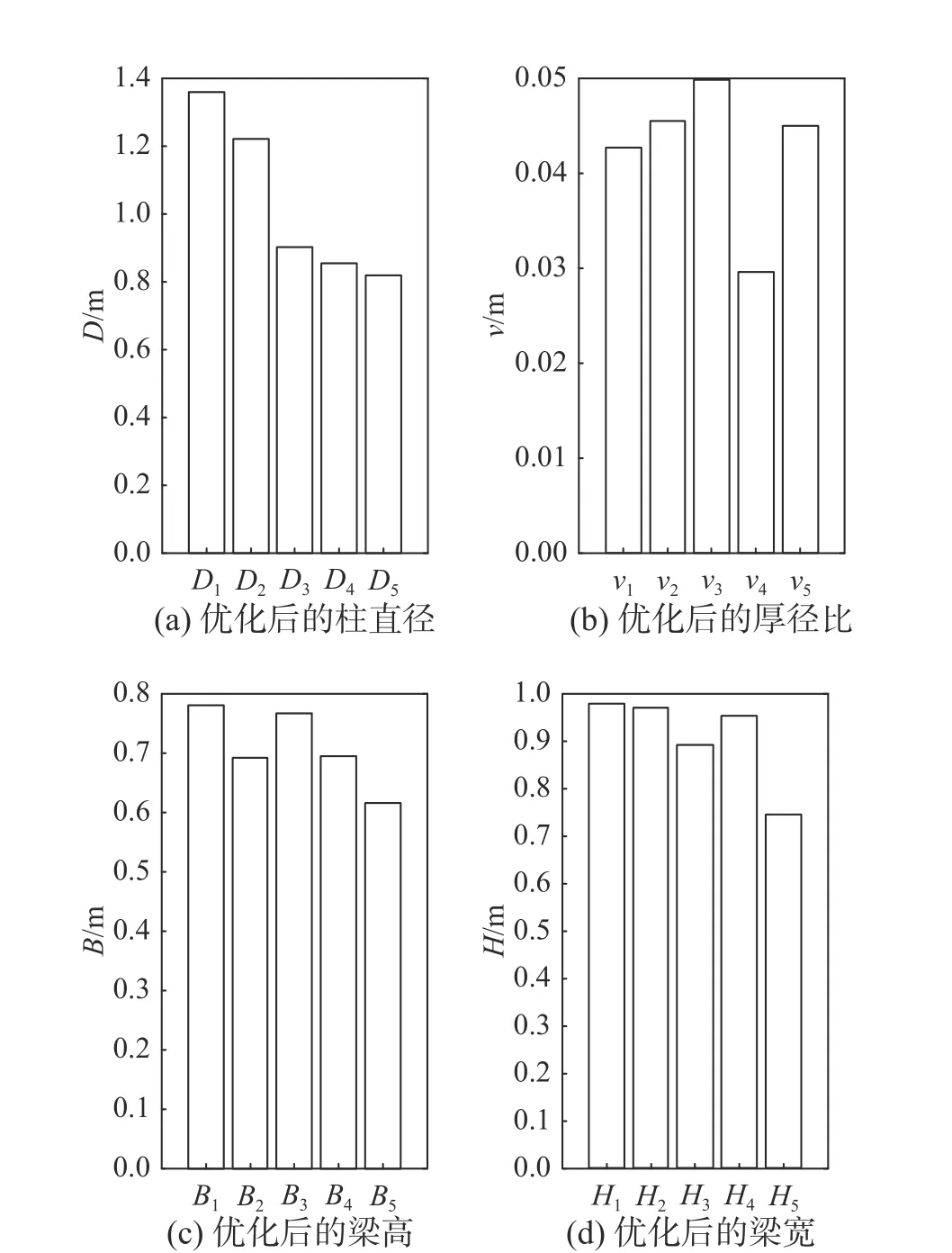
图12 截面尺寸优化后对比Fig. 12 Comparison between optimized section sizes

3.4 高层建筑结构拓扑优化设计

1) 基于变密度法的结构拓扑优化

根据Bendsøe 提出的材料最优分布，通过建立两点分布数学模型，将设计域中材料是否存在进行分类，数学表达式为：

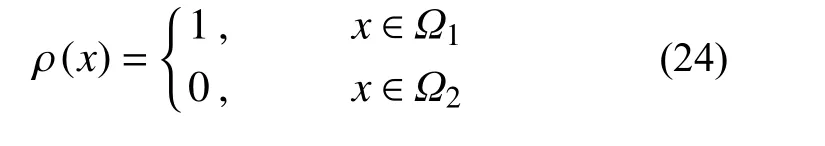
式中：1 表示有材料，0 表示无材料； Ω1表示实体材料区域， Ω2表示非实体单元区域。

以下以基于体积和位移约束下的塔架刚度优化为例，体积约束作为约束条件，得到基于SIMP方法拓扑优化问题的模型。

具有体积约束和位移约束的最大刚度拓扑优化问题可以表述为：

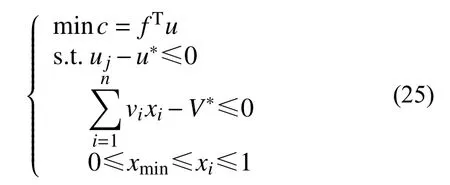
式中：c为柔顺度；uj为结构j点的位移响应，u*为结构j点位移响应限值；vi为每个单元的体积，xi为每个单元的相对密度；V为结构总体积，V*为结构总体积限值。

引入拉格朗日乘子λ、β，则基于体积和位移约束下的刚度优化问题，其对应的拉格朗日方程为：

本算例为9 层塔架结构。结构总高度H=27 m，层高h=3 m。结构中的所有梁、柱、斜撑截面均为等边角钢，其中柱截面边长a1=120 mm，厚度b1=10 mm；梁和斜撑截面边为a2=80 mm，厚度b2=8 mm。材料为Q235，弹性模量E=2.1×1011N/m2。由沿高度方向边长为3 m 的正方形钢框架组成，通过角钢柱和角钢斜撑相互连接。柱与梁、柱与斜撑均采用铰接，柱底与地面采用刚接。塔架结构三维模型及节点编号如图13(a)所示，塔架结构俯视图如图13(b)所示。

图13 九层塔架结构Fig. 13 A nine-story tower structure

本文利用分区拓扑优化方法，提高了搜索最优解的计算效率，减少了拓扑优化运算工作量。采用基于分解的多阶段设计策略，首先将问题分成一组较小的子问题。对于每一个子问题，只有一部分拓扑变量得到优化，而其他拓扑优化变量被认为是暂时固定和不活动的，通过引入非活动区域和目标区域的过渡区域，可减小非活动区域对整个结构拓扑优化的影响。将取塔架结构的BC面进行拓扑优化，将塔架分为3 个子区域(如图14)，第一子区域0 m～9 m，第二子区域9 m～18 m，第三子区域18 m～27 m。第一轮拓扑优化首先从第一子区域开始，直至3 个子区域都完成拓扑优化。约束条件为：小于原设计域体积15%，顶部位移限值54 mm。膜单元厚度取1 cm。

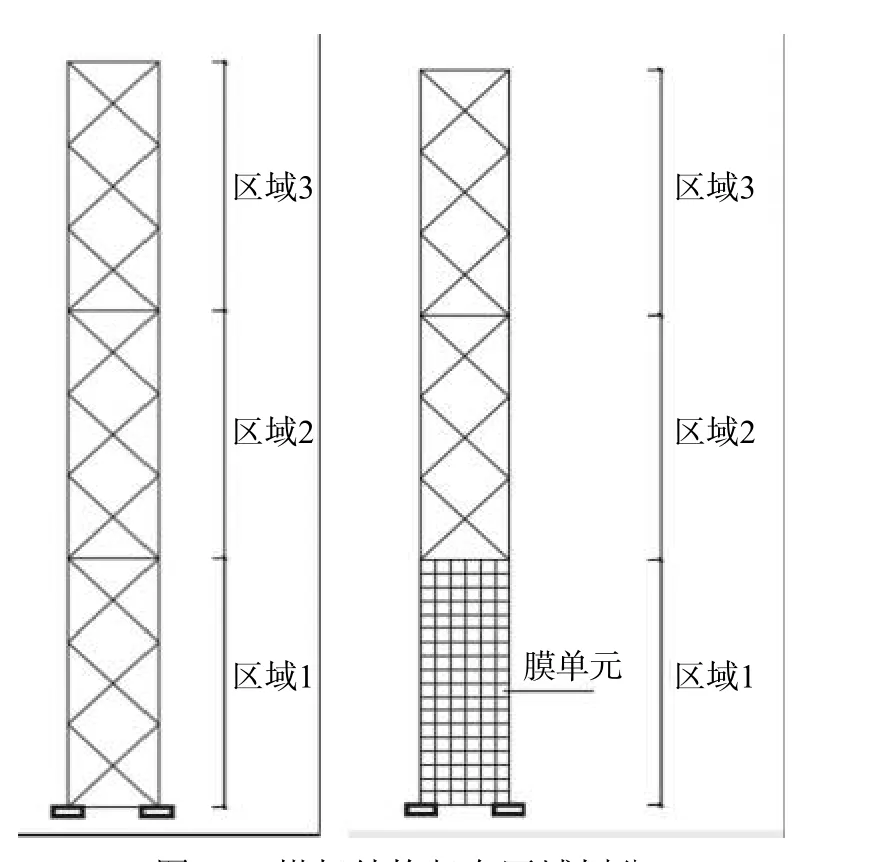
图14 塔架结构竖向区域划分Fig. 14 Vertical zooming of tower structure

塔架拓扑优化结果如图15 所示，塔架顶部位移随迭代次数变化如图16 所示，塔架体积随迭代次数变化如图17 所示。

由图15 可以看出，塔架斜撑最优分布为“X”形和“人”形组合，其中“X”形居多。由图16可以看，塔架顶部位移随着迭代次数增加不断下降，收敛时塔架顶部位移为23.75 mm，小于《钢结构设计规范》顶部位移限值54 mm。由图17 可以看出，塔架体积随着拓扑优化的进行初步收敛于规定的体积约束条件。

图15 塔架拓扑优化结果Fig. 15 Topology optimized results for the tower

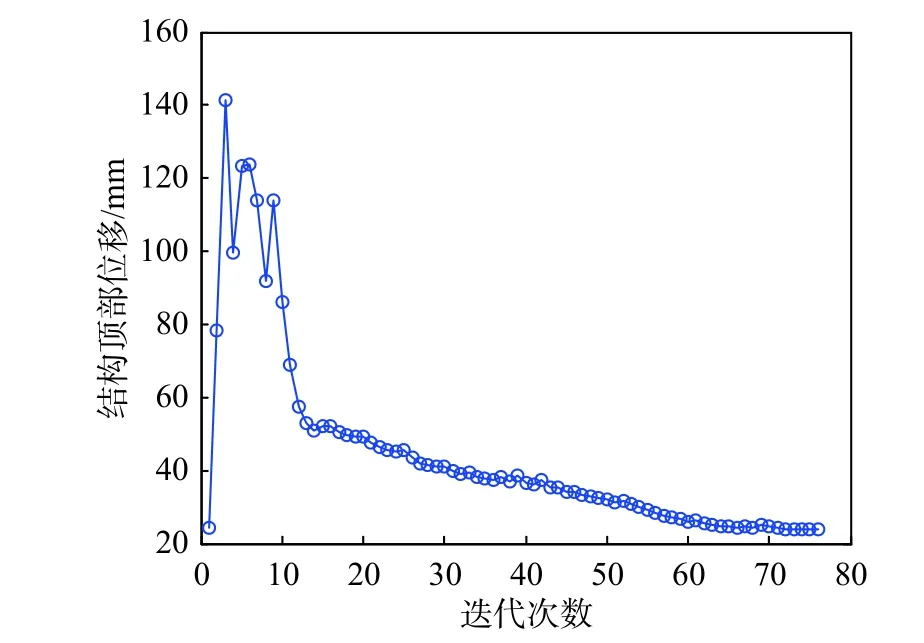
图16 塔架顶部位移随迭代次数变化Fig. 16 Variation of top displacement during iteration

图17 塔架体积随迭代次数变化Fig. 17 Variation of tower volume during iteration

2) 基于动态进化率的BESO 拓扑优化方法

目前双向渐进性拓扑优化方法基本采用预先设定的恒定进化率来进行单元的优化迭代。对于以全域为初始设计的拓扑优化问题，优化迭代方法需要在迭代初期快速去除不重要的单元，后期则需要降低进化速度，以保证迭代的收敛稳定性。

为了更快速地收敛，如果某一拓扑优化过程的进化率在所有的优化迭代中保持不变，则很难达到这一目的。引入动态进化率同时减少单次迭代有限元计算量和整个拓扑优化运算的迭代次数，使拓扑优化运算的计算效率能够满足拓扑优化需求，在动态进化率方面拟采用反正切动态进化率函数，如下式所示：

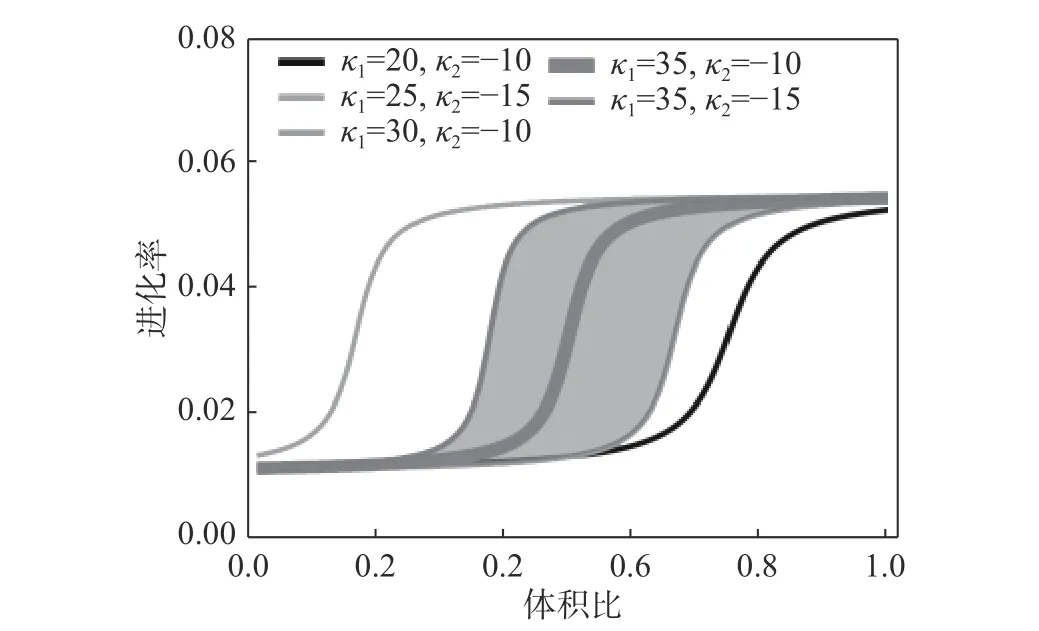
图18 拟采用的反正切动态进化率函数Fig. 18 Proposed dynamic evolution function in the arctangent form

3) 二维斜支撑拓扑优化设计算例

以支撑系统拓扑优化结构为例，从有限元分析的角度来看，意味着在优化过程中，一些被称为固定域的单元将永远不会被移除。为了解决这类问题，对固定域内的单元灵敏度赋以较大的值，以保证这些单元不会根据单元更新规则被删除。

在其他一些情况下，设计者希望结构由一系列具有相同拓扑结构的子结构周期性地组成，使整个结构更加简洁、美观。以矩形平面域为例，如图19 所示，可以将其划分为m1×m2的单元格，第i个单元格中的第j个单元表示为xi,j，在最优设计迭代中，xi,j可以是实的、也可以是空的。假设在某一设计域内总共有m=m1×m2个单元，则可以利用下式来保证所有单元中特定位置的单元同时被添加或移除：

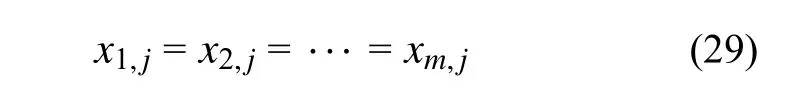
图19 3×2 个单元格的二维设计域Fig. 19 2D design domain with 3×2 cells

代表性单元格中第j个单元的灵敏度由所有单元格中第j个单元的联合变化引起的总体平均柔顺度的变化来定义，如下式所示：

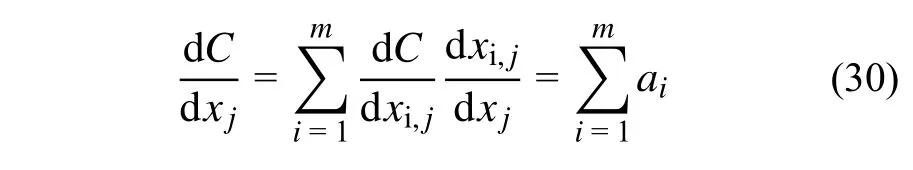
图20(a)展示了一块320 mm×80 mm×1 mm 的实体结构，其左边缘等距作用4 个集中荷载，分别为6000 N、6000 N、6000 N 和3000 N。材料特性如下：弹性模量E=200 MPa，泊松比ν=0.3，和质量密度ρ=7800 kg/m3。整个设计域被划分为320×80 的矩形单元。如图20(b)将结构的左、右、顶侧的最外层单元层视为不参与优化的固定域，其他内部单元视为拓扑优化的设计域。整个结构从上到下划分为4 个80 mm×80 mm 的区间。本例的目标是找出结构的最佳周期拓扑结构，使其在体积比不大于0.25 的情况下的平均顺应性最小化，本例的最优拓扑构型如图20(c)所示，类似的拓扑结构通常用于超高层建筑的支撑系统设计。

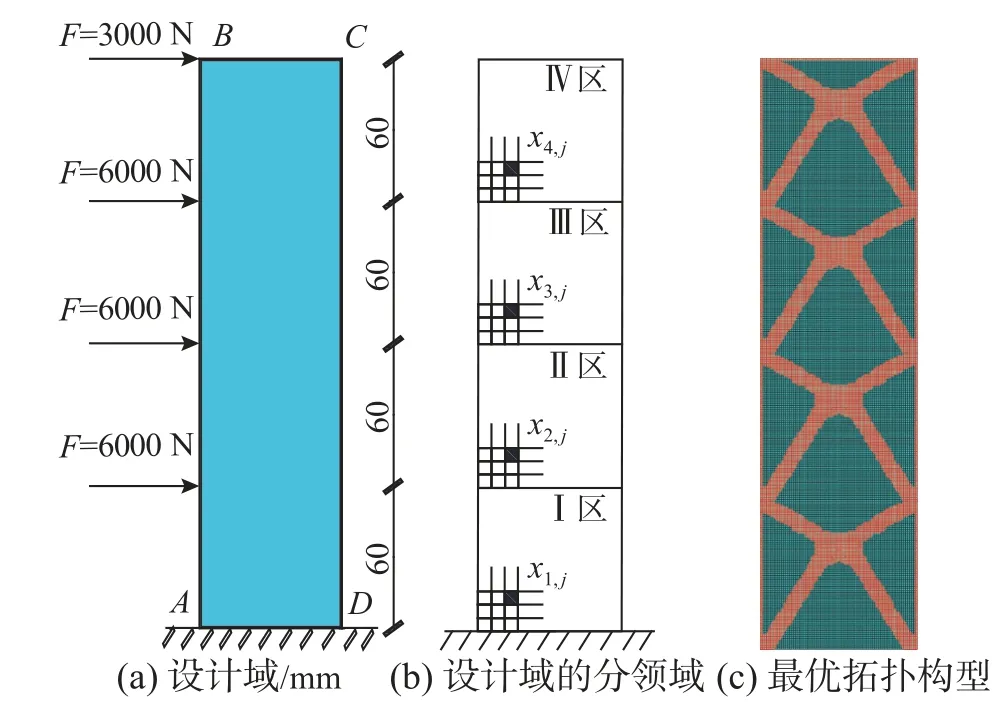
图20 支撑系统的设计域和最优拓扑Fig. 20 Design domain and optimized topology configuration of the bracing system

4 高层建筑的风振控制

我国东南及华南沿海地区为台风极端天气多发地，对于高层建筑而言，外形细长、质量轻且阻尼小等特征使其对风荷载变得敏感，风荷载已成为其抗风结构设计中必须考虑的主要控制荷载。本部分结合摩擦摆系统(friction pendulum system，FPS)限位复位功能和调谐质量阻尼器(tuned mass damper，TMD)耗能减振的优点，形成摩擦摆调谐质量阻尼器(FPS-TMD)[14,56]，以结构控制第三代Benchmark 模型—76 层钢筋混凝土建筑作为计算实例，研究顶部带FPS-TMD 系统的高层建筑风振控制效果。

4.1 FPS-TMD 系统风振控制设计

摩擦摆调谐质量阻尼器FPS-TMD 系统恢复力模型如图21 所示，假设滑块质量为m，滑道半径为r，滑块相对于主体结构顶层运动的转角为φ，滑块与滑动面的摩擦系数μk。

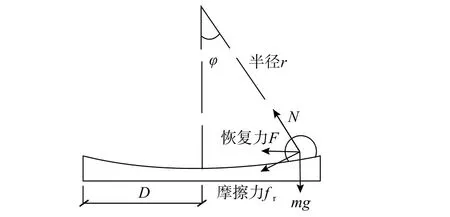
图21 FPS-TMD 系统恢复力模型Fig. 21 Restoring force model of FPS-TMD system

1) FPS-TMD 系统恢复力模型

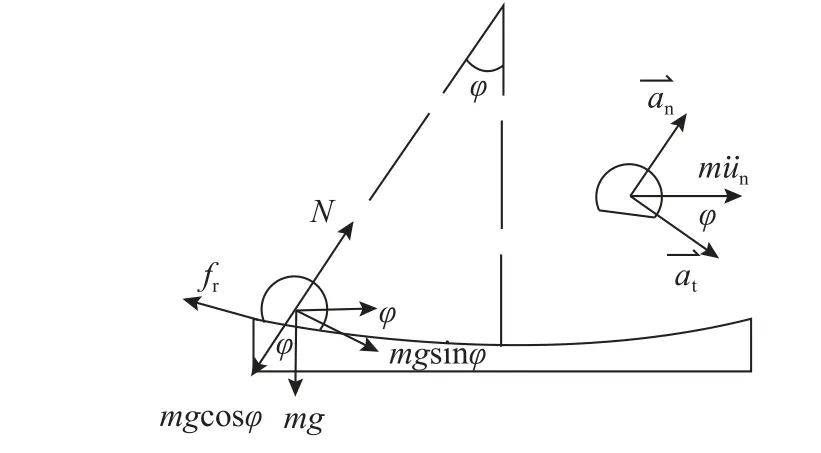
图22 FPS-TMD 系统风振模型Fig. 22 FPS-TMD system under dynamic wind loading

3) 顶部带FPS-TMD 系统的高层建筑结构风振动力方程的建立

顶部带FPS-TMD 系统的整体结构，受风荷载p(t)作用时的简化模型如图23 所示，主体结构可视为具有n个自由度的n层模型，第i层的质量为mi、层间刚度为ki，阻尼系数为ci(i=1,2,···,n)，FPS-TMD 系统滑块的质量、刚度和阻尼分别为md、kd、cd，风荷载pi(t)作用在各楼层集中质量mi处。

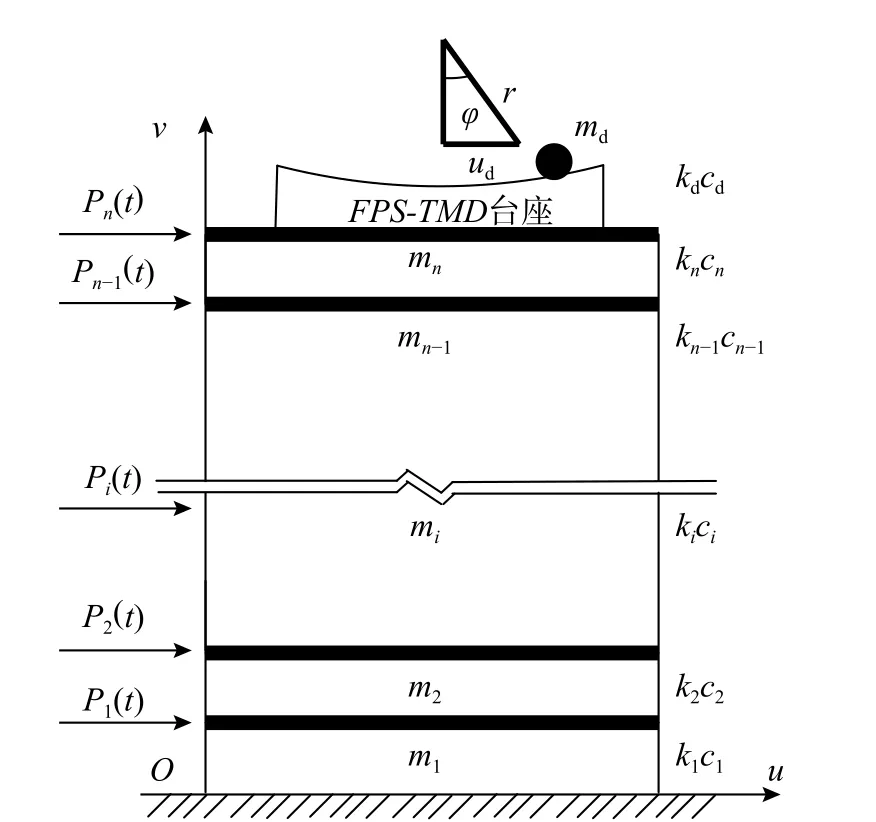
图23 顶层设置FPS-TMD 系统的计算模型Fig. 23 The simplified computation model of tall building with FPS-TMD system installed at top floor

本文以一栋76 层306 m 的结构控制Benchmark模型为例，其主体结构采用巨型框架-核心筒结构体系来承担重力荷载和风荷载，如图24、图25 所示。结构单方向前5 阶自振频率依次为0.16 Hz、0.765 Hz、1.992 Hz、3.790 Hz 和6.395 Hz，采用Rayleigh 阻尼模型来构造阻尼矩阵，假设建筑前5 阶振型阻尼比均为1%。为获得本建筑物的风荷载时程，进行了多点测压风洞实验[57]，风洞试验采样频率为1000 Hz，模型与原型比例为1∶400，速度比为1∶3，时间比为1∶133，原型10 m 高度标准风速为13.5 m/s。

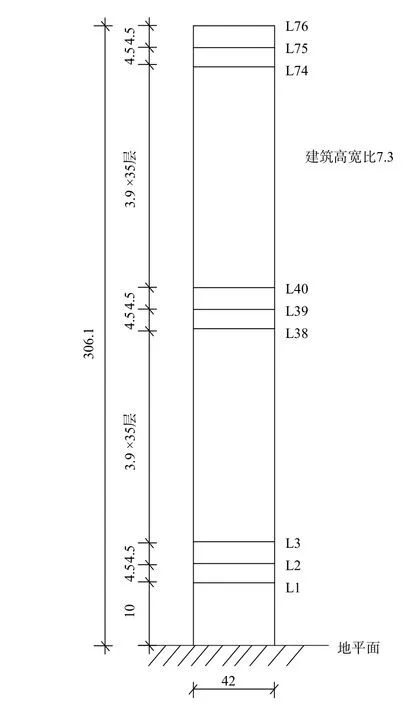
图24 Benchmark 模型 /mFig. 24 Benchmark model

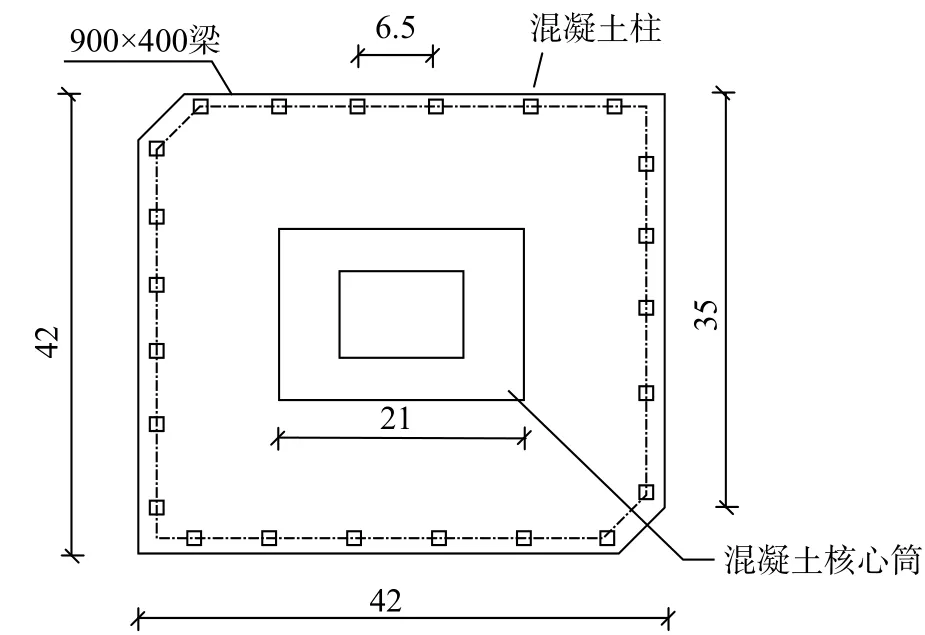
图25 巨型框架-核心筒结构 /mFig. 25 Mega frame-tube core structure

为简化结构动力计算，原结构可视为具有76 个节点的糖葫芦串模型，每个节点保留2 个平动自由度，共有152 个自由度，表示每层楼在X、Y方向上的位移，如图26 所示，通过静力凝聚法得到简化后的模型，以及对应的质量、刚度和阻尼矩阵[57]。风振响应计算过程中，顺风向风荷载时程由谐波叠加法模拟随高度变化的Von Karman脉动风速谱，形成对应的脉动风速时程后采用准定常假定得到，而横风向风荷载时程采用文献[57]提供的风洞试验结果。

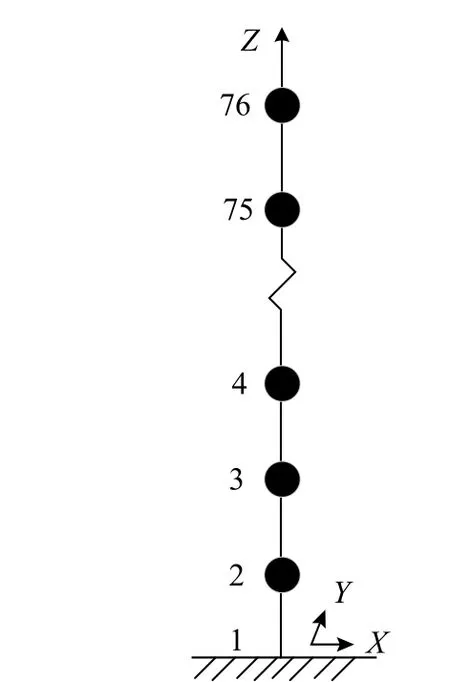
图26 多自由度集中质量模型Fig. 26 Simplified model with lumped masses

4) 顶部带FPS-TMD 系统的高层建筑结构风振响应分析

假设76 层Benchmark 模型处于广州市中心D 类地貌，其上部设置有单向FPS-TMD 系统，滑道半径根据FPS-TMD 系统第一阶自振频率近似等于主体结构第一阶自振频率的原则 确定为9.7 m，滑块质量取主体结构质量的1%，质量滑块在滑道中的摩擦系数取为0.01。则在不同重现期设计风速对应的横风向风荷载作用下，结构顶部风致位移、速度和加速度时程的均方根值及风振控制效率如表7 所示。

表7 结构横风向响应均方根值及风振控制效率Table 7 RMS values in across-wind induced response and control efficiency

由计算可知，同一重现期设计风速对应的横风向风荷载引起的结构顶层响应均比顺风向响应大。随设计风荷载增大，风致响应逐渐变大，同时FPS-TMD 系统的控制效果越好。横风向风荷载作用下，50 年和100 年重现期的加速度和速度控制效果相当，两者均优于位移控制效果，横风向下加速度最高减振效率可达41.28%，最低为13.79%，速度减振范围在19.72%～40.82%之间，位移减振效率则为14.29%～31.34%。

4.2 带FPS-TMD 系统高层建筑风振控制的实时混合试验

为验证带FPS-TMD 系统高层建筑在风荷载作用下风振控制分析结果的正确性，本文采用实验的方法加以验证，理论上可以采用振动台实验或风洞实验加以进行。然而对FPS-TMD 系统的高层建筑进行此类实验时，受整体模型试验缩尺比的限制，FPS-TMD 系统中的构件考虑缩尺效应后，其缩尺模型尺寸将会变得过小而难以加工。同时，当进行FPS-TMD 系统和下部高层建筑的整体模型实验设计时，两部分考虑缩尺比效应后，不一定都能同时满足动力相似比要求。在这种情况下可以借鉴Nakashima 等[58]提出的“子结构试验方法”，较好地解决上述问题。该方法将研究对象分成2 部分：一部分为结构受力性能比较复杂的部分，此部分由于其力学模型或分析机理不是十分明确，因此需采用原型试验方法，把其物理模型作为试验子结构进行分析；另一部分(例如高层建筑结构体系本身)由于力学特性已经很清楚，能够通过有限元等数值模拟的方法计算，该部分称为数值模型子结构。实时子结构试验的概念自提出以来，就引起了国内外专家学者特别是结构抗震设计领域的广泛关注[59-61]，但目前此类新型实验技术，在建筑结构抗风领域的研究和应用还十分少见。

对于FPS-TMD 系统的模型实验，以往大多采用地震振动台和相应的液压伺服式作动器。对于FPS-TMD 系统的力学性能和动力特征实验研究而言，当可以用较大的模型缩尺比进行模型实验时，其对应外加激励的幅值相对而言较小，此时如采用直线电机驱动的小型电振动台则具有反应速度快，实时性更好，更易于对其进行运动控制等优点，同时还可以减少大型振动台试验费用、模型加工成本高等不足之处。因此本文在借鉴直线电机驱动相关运动控制算法的基础上，研究采用直线电机驱动的小型电振动台，对带FPS-TMD系统高层建筑进行风振控制的实时混合实验方法。

在实时混合实验装置方面，通常是采用带实时操作系统的工业控制器来代替PC 机，以尽量避免PC 机与实验系统之间的时滞。目前，大型振动台实验一般采用美国MTS 公司Flex TEST 平台的数字闭环控制，以及对应的新型液压伺服控制系统，但相对而言，此类大型控制系统的编程太复杂，在进行混合实验时控制算法选择性差。另外，由德国dSPACE 公司开发的一套基于MATLAB/Simulink 控制系统的软硬件dSPACE 仿真平台，以及与其配套的直线电机加载系统，在工业设计领域有着较为广泛的应用。dSPACE 系统用于实时混合实验，功能也比较完善，在工业设计领域具有较广泛的市场，但由于其系统的封装性较强，因而对其进行二次开发，在其适用于建筑结构风振控制的实时混合实验方面则受到一定限制。

为此本文采用美国ACS Motion Control 公司的运动控制模块(包括运动控制器和电机驱动器)，利用美国NI 仪器有限公司Labview 软件与MATLAB/Simulink 的接口工具包(Simulation Intetrface Toolbox或Model Interface Toolbox)建立混合实验实时仿真系统，其总体架构如图27 所示[62-63]。本文开发的基于电机作为作动器的小型实时混合实验平台，相比于液压式作动器，电机驱动振动台具有反应速度快、实时性更好的优点，其加载和运动控制比传统的液压加载系统要相对简单。

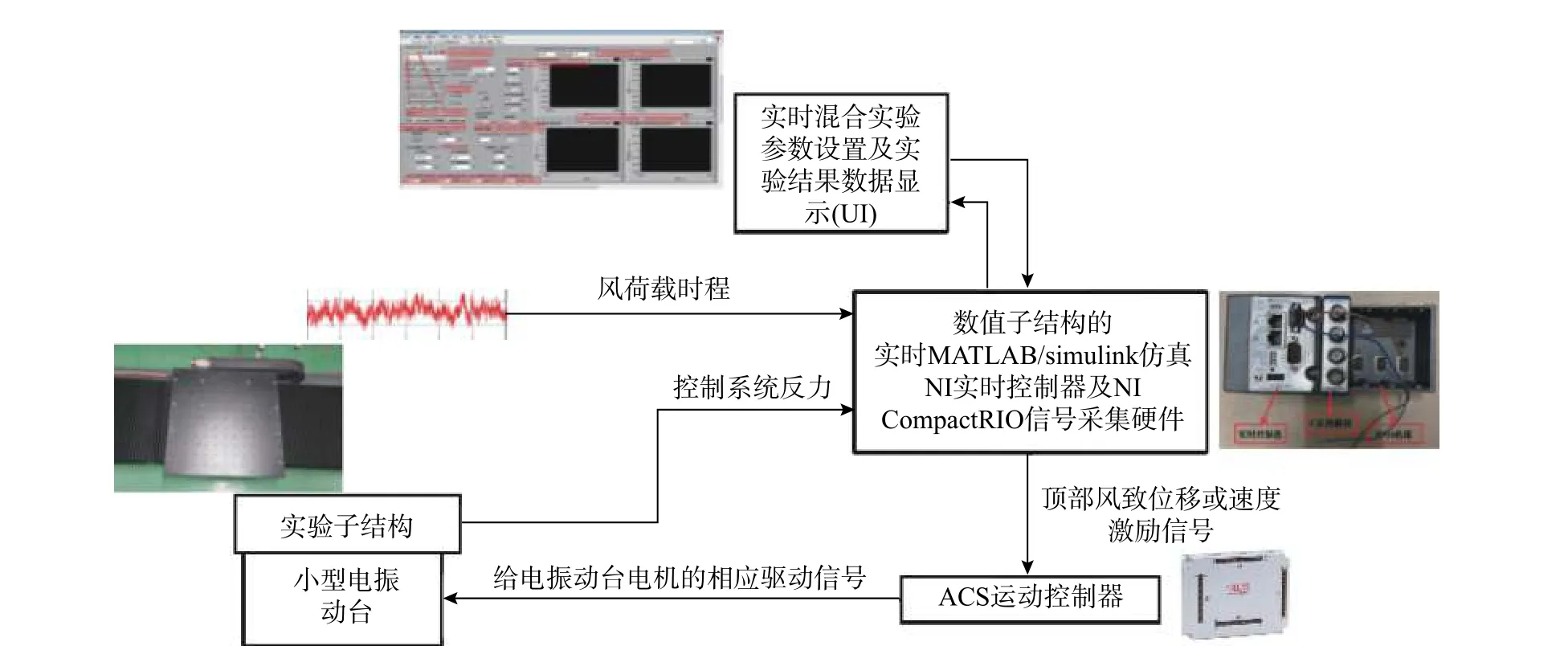
图27 带FPS-TMD 系统高层建筑风振控制实时混合试验平台的总体架构Fig. 27 The configuration of real-time hybrid test for wind vibration control of tall buildings with FPS-TMD system

1) 带FPS-TMD 系统高层建筑风振控制的实时混合试验结果分析

基于上述开发的实时混合试验平台，采用风洞试验得到的横风向荷载，对图24 所示的Benchmark 模型顶部设置FPS-TMD 系统后，其风振控制效果进行实验研究。如图28 所示为横风向100 年重现期风荷载作用下，Benchmark 模型主体结构顶层风致响应的数值模拟结果与实时混合试验进行对比，两者的吻合度很高。

图28 横风向100 年重现期风致结构顶部位移、加速度数值模拟与实时混合试验对比Fig. 28 Comparison results in the across-wind response with 100-year return period at top floor between numerical simulation and real - time hybrid test methods

表8 为横风向100 年重现期风荷载作用下的FPS-TMD 系统的控制反力和结构响应均方根值对比，其均方根值偏差在大多在10%上下波动。

5 结论

本文针对与高层建筑抗风优化设计和高层建筑风振的几个相关问题，采用最优准则法，主要研究了考虑风速风向联合概率分布和基于可靠度及性能化的高层建筑杆件截面抗风设计方法，以及基于改进罚函数的基因遗传算法和改进动态进化率的BESO 拓扑优化算法。通过相关算例分析，验证了本文提出的高层建筑抗风优化算法的有效性。在风振控制方面，结合摩擦摆系统和调谐质量阻尼器各自的优点，对FPS-TMD 被动控制系统的风振控制效率进行了数值模拟分析和实时混合实验的相关研究。本文主要结论如下：

(1) 风速的随机性和风向对结构风致响应的影响，是高层建筑抗风优化设计中必须考虑的重要因素。通过实际算例对比是否考虑风速风向联合概率分布和结构自振频率、阻尼比等变量随机性的高层建筑抗风优化结果发现，相较于以往确定性优化法，考虑上述变量随机性的优化结果显示：结构自振频率限值有所降低，优化结果更为合理，同时也进一步提高了优化空间。

(2) 基于改进动态罚函数及分级遗传算法，可使得优化工程中种群中不可行解与可行解的比例随代数的变化规律更合理，有利于扩大优化搜索空间，收敛效果更佳。

(3) 通过算例，分析不同的固定进化率对拓扑优化结果的影响，分析结果显示：基于动态自更新进化率的双向渐进结构优化方法，可以减少单次迭代有限元计算量和整个拓扑优化运算的迭代次数，同时使得拓扑优化结果更加稳定和高效。

(4) 采用数值模拟和实时混合试验两种研究方法，对FPS-TMD 被动控制系统对高层建筑的风振控制效率进行了综合分析，验证了本文提出的FPS-TMD 被动控制系统应用于高层建筑风振控制的有效性。同时，基于NI CompactRIO 系统的小型电振动台实时混合试验平台开发，为高层建筑风振控制的实验研究提出了新思路。