大跨度基准索股线形测量精度控制技术

王豪巍

(中海石油技术检测有限公司,天津 300459)

0.引言

随着当前建筑行业不断发展，工程规模不断增大，建筑结构也向着复杂化发展，使工程测量工作操作难度加大[1]。为保证工程测量工作的顺利开展，需深入分析对测量精度产生影响的因素。无论施工过程，还是维护工作都需以高精度的测量结果为依据。因此，测量精度控制技术研究是当前迫切需要解决的问题。所谓测量精度，是指工程的数据测量结果与实际结果的差异[2]。尤其在建筑工程经营维护阶段，更要通过控制测量精度，获取误差较小的线形测量结果，快速查找安全隐患，避免人们的生命财产安全受到威胁。王杰[3]根据测量技术要求，分析当前测量技术中的影响指标，提出与之相应的测量精度控制措施。在开展测量工作前，以科学测量勘测理念为基础获取现场数据，结合陀螺定向技术与三维激光测量技术，提升测量精度，但该测量控制技术工作效率较低。贺春梅[4]分析了工程测量精度要求，并按照项目测量要求设计精度控制技术的具体操作步骤。根据传统测量过程中存在的问题，分析产生影响控制精度效果的因素，确定工程测量精度控制技术的注意事项、实施措施。但该方法的精度控制效果较差。周瑜[5]分析了工程测量结果对监督工程质量安全的重要作用。在实际工作中，不精确的数据无法在工程建设中发挥作用，还会进一步加重工作负担。在测量工作中需将地面平面坐标系传送至测量点，根据一井定向方法进行测量，结合激光铅垂法克服钢丝摆动造成的误差。最后，通过计算机辅助工具，利用相关公式和概念控制测量精度。但该控制技术增加了测量成本。根据上述文献提出的控制方法问题，本文针对大跨度基准索股线形测量工作设计测量精度控制技术，从大气折光系数入手，改正单向三角高程方法的高差，完成测量精度的良好控制，保证线形测量结果满足工程要求。

1.大跨度基准索股线形测量精度控制技术设计

1.1 布置基准索股测量点

在大跨度基准索股测量过程中，测量结果受桥梁结构和外界因素的影响。线形测量主要包括跨度测量、基准索股里程、高程放样测量等内容。考虑到大跨度基准索股线的测量工程复杂性，故定位基准索股的重点结构。为完成测量精度控制，故选定最佳基准索股测量点。根据基准索股里程和高程测量需求，分别在中跨、边跨的跨中位置设计布设点，在整个桥体上共设置8个测量点，基准索股的测量点分布情况（如图1所示）：

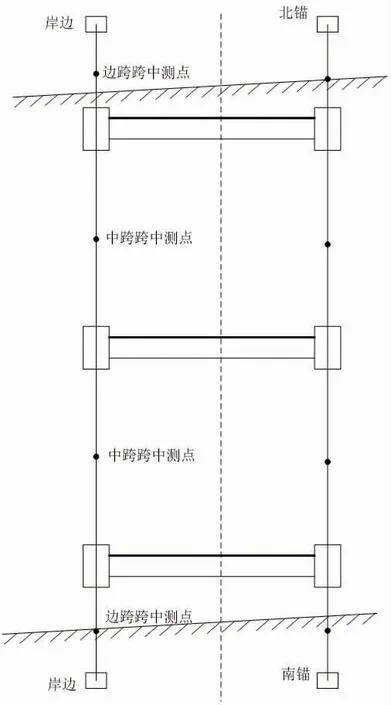
图1 测量点位布置示意图

根据基准索股线形测量特点，由图1可知：测量点布置情况，设计测量控制网。考虑到测站点与标点之间的距离和测量放样效率使测量精度降低，故在测量点选择时，分析不同测量点之间的相对关系，利用强制对中装置降低架站造成的误差。

在确定具体位置后，需在该位置安装棱镜作为主要辅助测量工具。考虑到基准索股表面特点，为解决棱镜安装问题，故制作与棱镜尺寸一致的夹具，保证每个夹具可放置一组棱镜。由于基准索股呈六边形，根据其尺寸将棱镜安置器设计为阈值尺寸相符的六边形。在棱镜安置器的两端安装长10 cm的铁杆，每个铁杆末端均安装反射棱镜。在测量工作开展时，以卡环两端棱镜作为辅助工具，获取测量点边长和高程。由于棱镜保持铅垂状态，故降低了立镜误差。针对布局合理的大跨度基准索股线形测量点，分别安装上棱镜和下棱镜，为后续测量精度控制工作提供有力支撑。

1.2 测定线形测量点高差

文中采用三角高程法在上述环境中展开线形测量工作，为控制测量精度，故对测量点高差进行高精度测定。按照大跨度基准索股的高程控制网设计需求，需要保证高程的测量精度。本研究在桥梁两岸分别放置高精度智能型全站仪，展开大跨度基准索股线形测量。三角高程测量原理（如图2所示）：

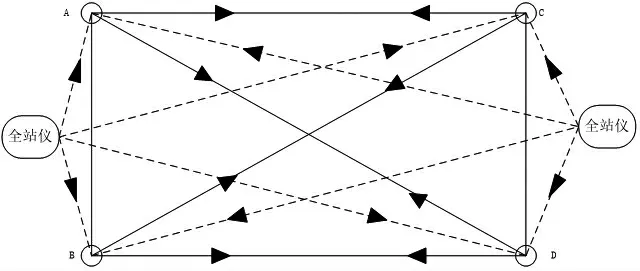
图2 三角高程测量过程示意图

根据图2的测量原理可知：在大跨度基准索股展开跨河三角高程测量时，需要根据实际测量环境，针对三角高程测量过程中的高程需求，在两岸主要位置设置多个临时测量点，如图2中的A、B、C、D。四个测量点平均分布在两侧岸边，A与B之间距离保持在20m-30m，C与D之间距离亦如此。除此之外，在跨河点50m附近区域安装两台全站仪，完成对测量点A、B、C、D的对向测量。在每个水准点上摆放三棱镜以辅助测量工作。在智能型全站仪的作用下，获取4个三棱镜的斜距、垂直角。由于全站仪作为自由测站，故不必担心因全站仪高度产生的量测误差。测量精度控制技术的开展仅需考虑临时跨河水准点与安装棱镜之间的误差。应用全站仪加定长棱镜开展对棱镜高的测量，测量原理（如图3所示）：

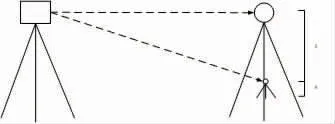
图3 基座棱镜高测量原理

由图3可知：基座棱镜高测量依旧采用中间法三角高程法获取计算结果，将测量结果误差控制在0.3mm以内。针对跨河点棱镜，需要两台全站仪多次对斜距和垂直角进行测量，测量技术要求依据相关规范执行，以获取图2中AC、AD、BC、BD间的高差。在互差检验后使其互差满足测量要求，实现测量精度的初步控制。

1.3 计算大气折光系数

文中应用单向三角高程测量方法获取大跨度基准索股线形测量结果，以垂度线形测量为例，在实际操作中索股绝对垂度测量精度受大气折光系数影响较大。为控制测量精度，在基准索股线形测量工作实施前，多次测量该区域的对向三角高程，推算出测区大气折光系数，将其表示为K值。根据分析可知，某区域的K值测量结果往往与测区平均K值保持一致，除了大面积水域使K值变化方向产生变化外，还因气象和环境因素使不同时段的K值变化较大。所以，在进行基准索股线形测量精度控制设计时，对大气折光系数进行计算。根据观测位置和目标地点位置，计算两点之间的高差，计算公式如式（1）所示：

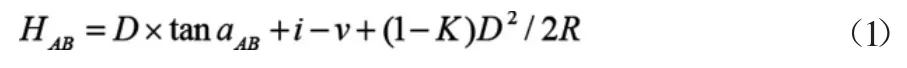
式（1）中，D为两点之间的平距；tan为正切函数；a为垂直角度；R为地球曲率半径；K为大气折光系数；i为仪器高度。根据式（1）反推，获取大气折光系数的计算公式如式（2）所示：

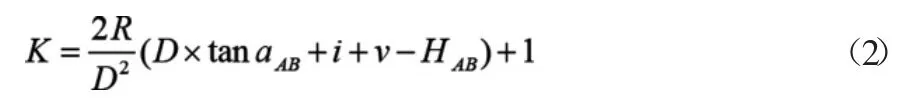
根据式（2）对测量区域一天内不同时段的大气折光系数变化进行计算，并应用测量时间内的大气折光系数改正测量高差。大跨度基准索股的温度随环境而改变，变化规律不完全相同。在线形测量工作开展时，选择风力在10m/s以下的天气，每次间隔1小时测量一次大气折光系数，并汇总形成表格。根据测量时间的平均折光系数K值，调整索股计算参数，实现单向三角高差改正。针对某一测量边AD，展开单向三角高差折光系数改正计算。根据单向三角高差的实测结果和大气折光系数条件，改正高hAD差表示如式（3）所示：

式（3）中，S0为A、D两点之间的实测平距。根据上述计算结果，用改正后的高差替换原本的三角高差，实现线形测量精度的进一步控制。

1.4 实现测量精度控制

在完成上述测量控制操作后，可以得到与实际结果误差较小的测量值，为保证测量精度实现最优控制，需借助计算机辅助工具，根据测量精度控制目标，利用计算机相关函数生成测量精度控制优化函数，函数表示如式（4）所示：

式（4）中，ΔL为测量误差变量，min为最小值；f为测量频率；v、v'分别为理想测量数据传输速度和实际测量数据传输速度；σ为测量装置本身原因造成的误差；λ为其他干扰因素造成的误差。根据上述公式提出的各种精度控制影响因素，文中将遗传算法与RBF神经网络融合，以最小测量误差为目标函数，展开目标函数求解。由于RBF神经网络的结构中包含3层前向传递结构，以此为基础结合遗传算法，计算神经网络中隐含层数量，从而求解神经网络应用过程中的各项参数。

此外，应用二进制编码方法将神经网络中的多项参数以编码形式表现，便于计算机识别。通常情况下网络输入节点数量即代表编码长度。结合遗传算法进行网络训练，获取适应度函数极值。适应度函数fitness的计算结果如式（5）所示：

式（5）中，i为网络训练数据；j为输出节点；Y、Y分别为训练时的实际输出和期望输出；N为样本个数；M为神经网络输出节点数量。通过式（5）进行混合神经网络的误差计算，实际计算流程包括三个环节。首先，进行20次的基准索股线形测量，将测量结果作为混合神经网络的初始群体，通过测量结果计算出由于各种因素造成的损耗数值，将数据转换为二进制编码的形式，展开网络训练。在设置合理的迭代次数后，获取适应度函数计算结果。然后，根据上述计算的适应度函数结果，将其作为起始参数输入混合神经网络，在遗传算法作用下，经过进化计算、变异计算和遗传计算，得到测量误差计算值。最后，根据历史测量结果，对该计算流程进行校正，将数据误差的平方值作为终止条件，完成混合神经网络求解操作的终止。将求解结果作为大跨度基准索股线形测量精度控制技术的基础，设计测量装置控制器。完成对测量精度的实际控制，使测量结果更符合工程需求。

2.应用实例

2.1 工程概况

为测试本文设计技术的实际应用效果，将测量精度控制技术应用于秀山大桥的基准索股线形测量项目。该桥体位于我国浙江省境内，连接岱山岛和秀山岛，属于大跨度桥体结构。秀山大桥主体结构是双塔自锚式悬索桥，结合门式桥塔，并在桥塔顶部设置主索鞍，具体结构（如图4所示）：

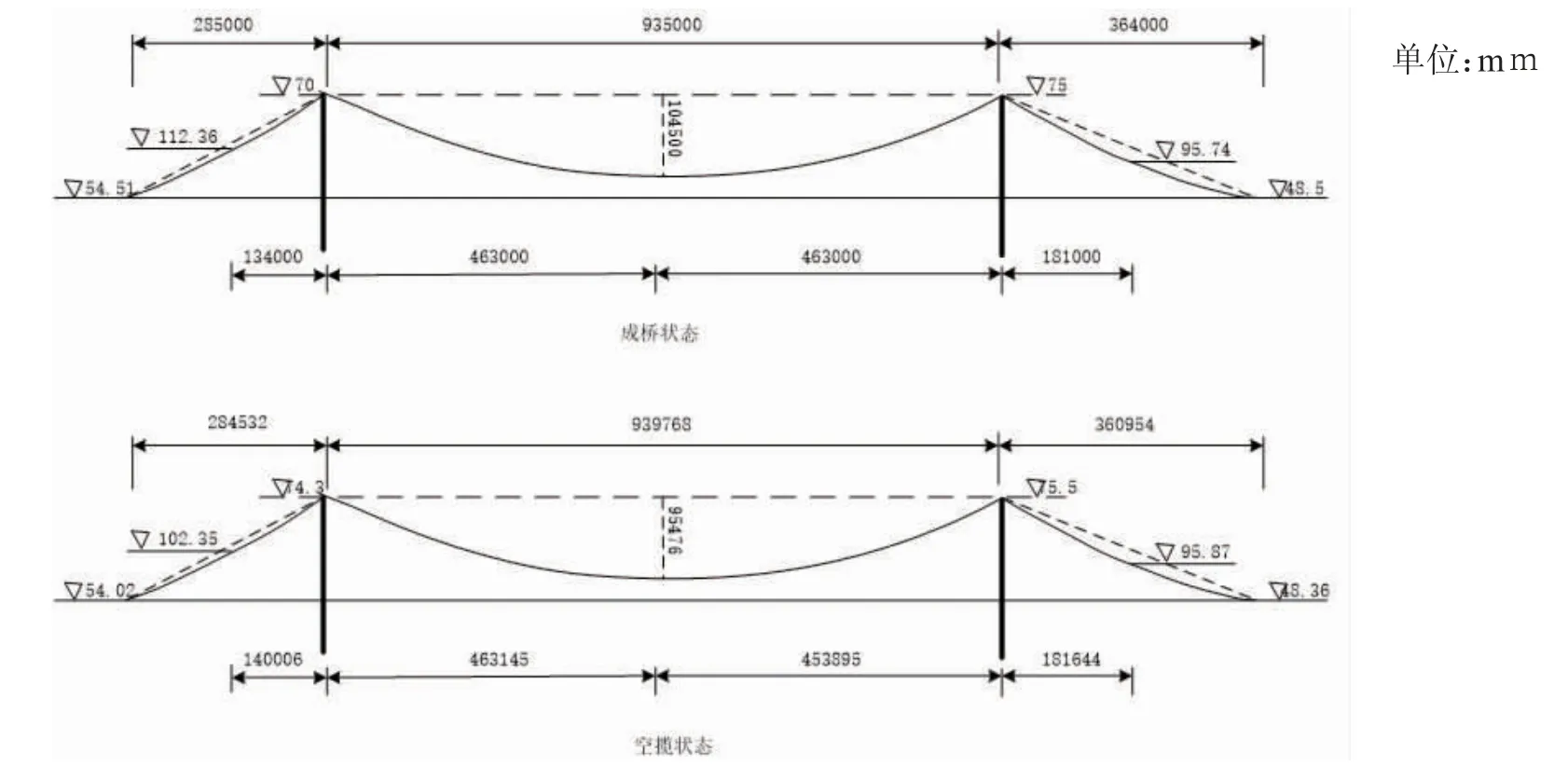
图4 主缆布置图

该桥梁的缆跨总长1584m，主缆由锚跨、边跨、中跨共同构成。在基准索股线形测量过程中，根据以往数据可知各跨跨中标高变化与索长变化关系，其中锚跨为1∶7.31，边跨为1∶4.63，中跨为1∶1.84。并且，在近似正六边形的索股架设过程中呈现逐层排列的特点，主缆结构（如图5所示）：

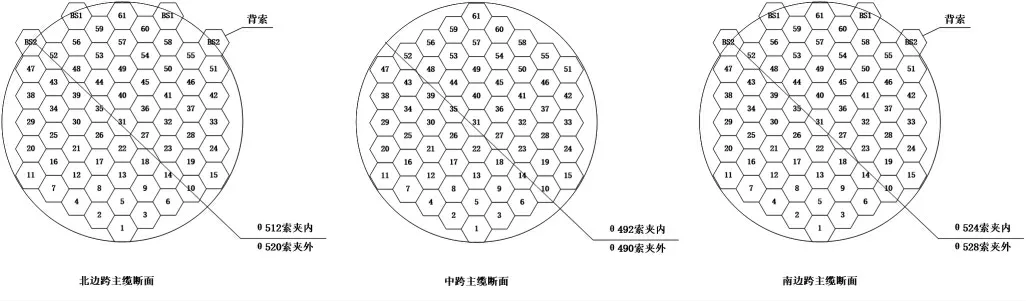
图5 主缆结构图

根据主缆结构图发现，通过定形捆扎的方式将数十根索股结合成单根，形成秀山大桥的主缆。除此之外，为保证桥梁结构稳定性，在桥梁边跨位置安装4根背索，并将其固定在大跨度桥梁的主索鞍上。基于上述实际情况，展开基准索股测量工作，并分析本文设计的测量精度控制技术应用效果。

2.2 基准索股测量

基准索股线形测量过程中需完成锚跨里程及标高、主缆垂度标高等多项测量项目。在基准索股跨中位置安装棱镜，并最大程度去除棱镜杆不垂直索股产生的误差，以达到控制测量精度的目的。本文采用正六边形整形器设计工装夹具，利用棱镜杆将两个棱镜相连（如图6（a）所示）。在实际测量时，通过中间正六边形工装夹具，将两个棱镜固定在索股合适位置（如图6（b）所示）：

图6 索股工装夹具图片

获取上、下棱镜杆高程H上、H下，计算索股中心点高程如式（6）所示：

通过式（6）计算，得到棱镜杆高程的平均值，消除了由于棱镜杆不垂直造成的索股误差。安装棱镜后，寻找合适位置安装全站仪，利用三角高程测量方法获得测量结果。

本文采用的单向三角高程测量方法在测量精度控制过程中，需要针对大气折光系数进行高差修正。所以，需要在秀山大桥附近测量不同时段的大气折光系数，根据测量结果，形成不同时段大气折光系数统计（如表1所示）：

表1 大气折光系数统计

从表1可以发现，该区域不同时段的大气折光系数具有较大变化。其中，K值最为稳定的时段是夜间11点到次日凌晨5点，基准索股测量选定于该时段。通过分析大气折光系数对单向三角高差产生的影响可知，此时的测量结果会产生20mm以上的误差。根据大气折光系数修正高差值，实现大跨度基准索股线形测量精度提升，为后续测量工作提供参考。

根据研究可知，为保证基准索股线形调整工作的顺利进行，需要保证测量误差小于10mm。在完成上述仪器安装和参数修正后，进行连续三天的基准索股线形测量数据监测，以分析本文设计技术的测量精度控制效果。

2.3 测量结果与分析

通过上述操作，基于基准索股的线形测量分别在桥梁两岸设置双测站，获取垂度测量结果。利用改正后的单向三角测量法获取平均垂度测量值，并将其作为跨中点的最终垂度。首先，对主跨上、下游侧基准索股垂度进行测量，测量时间为3天，每天进行4轮测试，记录垂度测量结果。本文由于篇幅所限，仅展示上游侧基准索股中跨跨中垂度测量结果（如表2所示）：

表2 上游跨中垂度测量结果

应用本文设计的精度控制技术，展开基准索股线形测量，得到垂度测量值。通过分析表2可知：所有测量结果的垂度值互差总是低于10mm，符合大跨度基准索股线形测量要求，彰显本文提出技术的可靠性。

之后，对基准索股线形测量相对垂度进行3天监测，本文测量结果呈现相对垂度偏差（如图7所示）：

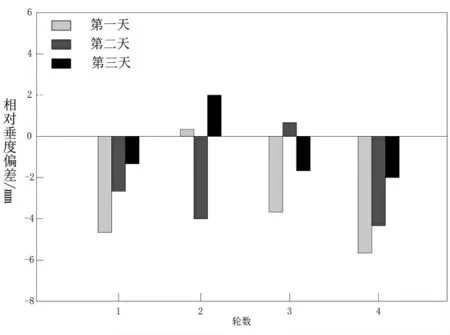
图7 基准索股线形测量相对垂度偏差统计

经过为期3天的测量后，根据相对垂度偏差统计结果可知，基准索股线形测量的最高偏差为5.7mm，最低偏差仅0.4mm。通过计算得出，基准索股线形测量平均相对垂度偏差约2.3mm。综上所述，基准索股线形测量中对垂度偏差远低于10mm，满足了大跨度基准索股线形测量精度要求，可以提升对工程总体现状的了解，有助于辅助工程经营管理。

3.结束语

由于建筑工程技术发展速度不断提升，出现多种样式的大跨度桥梁结构，所以工程测量精度要求越来越高。大跨度基准索股结构的测量受日照、风力及建筑结构的特殊性影响，导致线形测量误差较大。为保证桥梁后期运行维护工作的顺利进行，本文设计测量精度控制技术，以大气折光系数为基础，完成单向三角高程测量方法的参数修正，使基准索股线形测量满足精度要求。通过实例应用可知，本文提出的测量精度控制技术具有良好的可行性，推动了基准索股线形测量调整工作。由于研究时间约束，本文提出的技术仍存在不足，未来可以针对其他外界影响因素所产生的测量误差进行研究，进而推动测量控制技术的发展。