内嵌局域共振型散射体结构的低频吸声性能研究

罗英勤， 楼京俊， 张焱冰

(海军工程大学 舰船与海洋学院，武汉 430000)

在黏弹性材料中引入散射体作覆盖层被证明是有效的潜艇隐身手段[1]。该结构利用共振使耗散效率低的入射纵波向高耗散横波转化；利用粒子间的多重散射效应改变并增加入射波传播路径；利用基体材料阻尼特性对入射声波进行耗散。散射体包括单极和偶极形式，单级形式为各种各样的腔[2-5]，偶极形式的主要是大密度球[6-7]。但是这种传统设计的隐身材料已很难对抗工作频率日益降低的声呐探测。

近年来局域共振声学超材料迅猛发展，其超常吸声效应也备受关注。2000年Liu等[8]首次提出了局域共振声子晶体，其低频带隙处声波波长大于散射体尺寸两个数量级，为小尺寸控制大波长开辟了新思路。但是很多研究成果仅适用于空气中，水下吸声成果较少。Zhao等[9]在水声吸声材料聚氨酯基体中引入硅胶包覆的金属球作为局域共振散射体，在低频段实现了很高的吸声系数，为覆盖层设计提供了重要技术途径。吸声效果通过试验进行了验证，并采用多重散射理论对其吸声机理进行分析，表明纵波在局域共振散射体的作用下更容易转化成易耗散能量的横波且吸声峰频率与金属球密度关系密切。但是文中仅对第一吸声峰进行了分析。Wen等[10]采用多重散射理论和有限元方法进一步对该结构吸声性能进行了分析，建立了周期单元的共振模态和吸声谱之间的关系，通过分析吸声峰对应的位移云图解释了吸声机理，结果表明第一吸声峰是由金属球芯平动共振引起，第二个是由包覆层旋转共振引起且纵波模式向横波模式转化更多，能量消耗更多，吸声系数更高，吸声频带更宽。吕林梅等[11]采用简化的有限元方法对含有不同形状局域共振散射体结构的声学性能进行分析，结果表明：相同截面的球型散射体和圆柱形散射体第一吸声峰接近；相同体积不同高度半径比的圆柱型散射子吸声性能变化较大。Meng等[12]采用遗传算法对两层含有不同球型局域共振散射体的吸声材料进行了优化设计，得到了吸声频带更宽的优化结果并进行了试验验证。Shi等[13]研究了多层局域共振散射体结构对宽频吸声的作用。Zhong等[14]讨论了局域共振散射体内大密度芯体的位置对其吸声性能的影响。综上所述，内嵌局域共振散射体的水下吸声结构，第一吸声峰与芯体密切相关，第二吸声峰与包覆层密切相关，局域共振散射体的形状对声学性能影响很大。但目前文献主要对球型和圆柱型散射体进行了设计，缺少对其他形状散射体的讨论。

内嵌局域共振散射体结构的吸声特性分析方法主要有多重散射理论和有限元方法。多重散射理论计算方便，可以通过Mie矩阵分析波模式转换，便于分析吸声机理，但不适用于形状复杂散射体或者多种类型散射体组合形成的周期结构。有限元方法不受几何形状限制，且日益发达的计算机技术和日益完善的商业软件为大规模、高精度建模提供了更多可能，丰富的后处理接口也为吸声机理的分析提供了便利。另外，针对结构的周期性，可通过施加周期性边界条件仅对单个胞元进行建模分析[15]；针对结构的对称性，可通过施加对称性边界条件仅对单个胞元的1/4或1/8甚至是二维轴对称截面进行建模分析[16]。赵宏刚等用有限元方法对周期性局域共振散射体结构进行了建模分析，结合位移云图揭露了空腔散射体和局域共振散射体的吸声机理。吕林梅等将周期性局域共振散射体结构简化为1/8单元模型进行分析，结合位移场讨论了不同形状散射体的吸声规律。轴对称周期性局域共振散射体结构可以进一步简化为二维轴对称模型，可以在大量反复计算的优化设计中大大降低计算量，但是目前未见有文献对此方法进行应用和验证。

本文首先对轴对称周期性局域共振散射体结构建立二维轴对称仿真模型并验证其正确性。然后讨论了截面形状、芯体材料、包覆层厚度等参数对局域共振散射体结构吸声性能的影响规律。最后采用遗传算法对变截面局域共振散射体结构参数进行了优化设计，优化后吸声性能明显提高。为潜艇隐身覆盖层结构设计提供了重要参考。

1 结构模型与分析方法

1.1 局域共振散射体模型

整个吸声结构由黏弹性材料聚氨酯基体、软硅橡胶包覆层和大密度钢制芯体构成。如图1所示为笛卡尔直角坐标系下的周期性局域共振散射体结构单元。设吸声结构在xoy平面无限延伸，局域共振散射体为正方形周期排列，x和y方向基矢均为a。如图1(a)所示为球型局域共振散射体模型，包覆层厚度为t，芯体半径为rx。如图1(b)所示为圆柱型局域共振散射体模型，模型厚度为H，包覆层厚度为t，芯体为半径为rx高为l的圆柱。吸声结构前端为半无限水介质，一列平面纵波从其中垂直入射至结构表面，吸声结构后端为半无限空气介质。

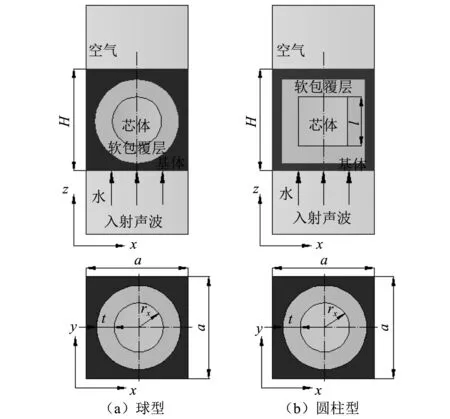
图1 局域共振散射体结构单元示意图Fig.1 Schematic diagram of local resonance scatter structural unit

1.2 轴对称模型的简化有限元法及验证

采用有限元方法建立声固耦合方程为

(1)

式中：M，C，K，R分别为质量、阻尼、刚度矩阵和声固耦合矩阵； 下标s和f分别为结构和流体；ue和pe分别为结构节点位移和流体的节点声压；Fs和Ff分别为结构受力和声压激励；ρf为流体密度。流体介质两端分别施加PML层形成吸声端面以模拟无限介质边界。结合边界条件和式(1)可以求得结构节点位移ue和流体节点声压pe。然后反射系数R和透射系数T可以求得，则吸声系数为

α=1-R2-T2

(2)

将图1所示的立方体周期单元转化为圆柱周期单元，保持内部散射体结构不变，将基体转化为同体积同高度的圆柱。此时整个模型符合轴对称条件，采用COMSOL Multiphysics建立二维轴对称仿真模型，如图2所示。为了模拟周期性，在轴对称模型柱面边界1、边界2、边界3设置法向位移为0。

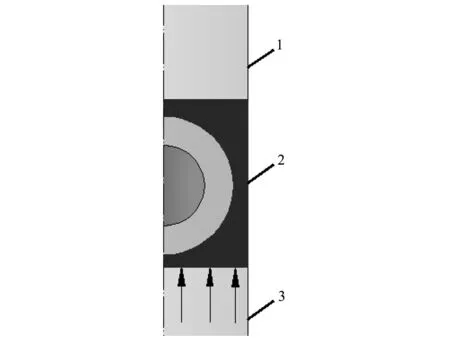
图2 二维轴对称模型示意图Fig.2 Schematic diagram of two-dimensional axisymmetric model

图1(a)所示模型几何参数如表1所示，材料参数如表2所示，采用简化方法对其吸声性能进行计算，研究频段为500～3 000 Hz，步长取为10 Hz。建模过程最大网格尺寸设为3 mm，满足精度要求的1/4最小波长。计算结果如图3所示。通过与Wen等研究中的仿真值对比验证了本文简化方法的准确性。

表1 球型局域共振结构几何参数Tab.1 Geometric parameters of spherical local resonance structure mm

表2 局域共振结构材料参数Tab.2 Material parameters of local resonance structure

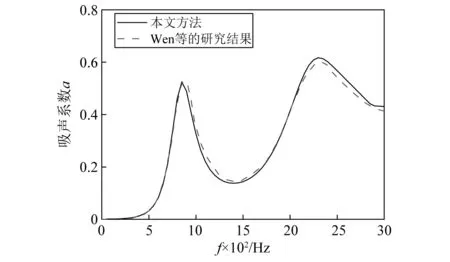
图3 吸声系数曲线对比图Fig.3 Comparison of sound absorption coefficient curve

2 吸声性能参数影响规律分析

2.1 截面形状对吸声性能的影响

为讨论散射体截面形状对吸声性能的影响，保证芯体体积、芯体z方向最大截面面积、包覆层厚度不变，将图1(a)所示的球型散射体芯体变换为圆柱、圆锥台1和圆锥台2等柱型散射体，包覆层厚度均为2 mm，圆柱型散射体示意图如图1(b)所示，圆锥台1和圆锥台2散射体芯体截面如图4所示。各模型芯体尺寸如表3所示。

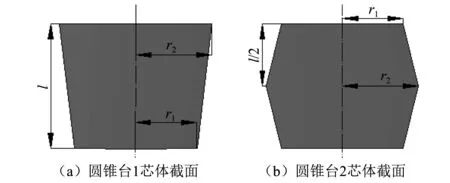
图4 芯体截面示意图Fig.4 Schematic diagram of core cross section

表3 各形状芯体尺寸Tab.3 Geometric sizes for Cores of various shapesmm

截面形状对结构吸声系数的影响如图5所示，各散射体结构在研究频段内均出现了2个吸声峰，第一吸声峰较窄，第二吸声峰更宽，规律与Wen等研究中的一致。散射体形状对第一吸声峰影响较小，但第二吸声峰发生了很大变化。图6(a)～图6(d)给出了各形状对应结构第一吸声峰处的位移分布图，图中箭头表示位移矢量，图6(e)～图6(h)分别为对应形状散射体结构的能量耗散密度分布图。由图可知，散射体运动主要表现为芯体在z方向同等位移幅值的刚体平动；芯体的平动带动软包覆层相应运动，导致包覆层位移幅值由内向外逐渐减小，能量主要在包覆层中耗散；最外层基体的位移很小，对应能量耗散很小，最终能量主要由散射体吸收，表明各形状散射体结构第一吸声峰由芯体平动共振产生。此时位移模式可以认为芯体和包覆层类似组成了一个质量弹簧模型，芯体作为刚体质量，包覆层作为弹簧系统。不同形状散射体的芯体体积保持一致，包覆层厚度一致，因此弹簧质量模型的固有频率变化不大。芯体产生平动自由度，包覆层弹簧随之产生剪切变形自由度，纵波通过平动位移引起剪切变形向横波的转换。横波在黏弹性材料中耗散更快，从而增加能量吸收提高吸声系数。

图7(a)～图7(d)给出了各形状下第二吸声峰处的位移云图，图7(e)～图7(h)分别为对应形状散射体结构的能量耗散密度分布图。由图可知，各形状散射体都发生了包覆层的旋转振动，同时圆锥台1和圆锥台2散射体结构的基体在入射侧和透射侧发生了不同程度的耦合共振，芯体位移也很小。能量主要在包覆层及临近基体内耗散，表明各形状散射体结构第二吸声峰与包覆层和基体密切相关，相比于第一吸声峰，基体的能量耗散在第二吸声峰增幅较大，但主要在包覆层内耗散。不同形状散射体的共振模式发生了变化，这对波型转换产生很大影响，导致吸声系数差异很大。

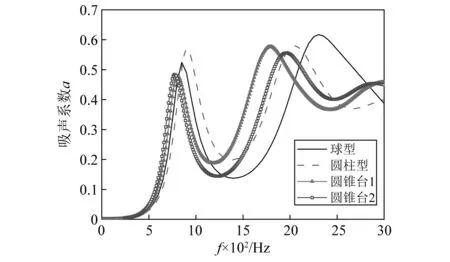
图5 散射体形状对吸声系数的影响Fig.5 The influence of the scatter shape on the sound absorption coefficient

图6 各形状散射体第一吸声峰处中面位移云图和能量耗散密度云图Fig.6 The mid-plane displacement and energy dissipation density fields at the first sound absorption peak of scatterers

图7 各形状散射体第二吸声峰处中面位移云图和能量耗散密度云图Fig.7 The mid-plane displacement and energy dissipation density fields at the second sound absorption peak of scatterers

2.2 芯体材料对吸声性能的影响

实际应用中，柱型局域共振单元芯体制备工艺简单，软包覆层的工艺也更易实现[17]。以图1(b)所示的圆柱型局域共振散射体结构为研究对象，讨论芯体材料对吸声性能的影响规律。芯体材料分别取为铝、钛合金、钢、镍合金和铅。芯体材料对结构吸声系数的影响如图8所示。

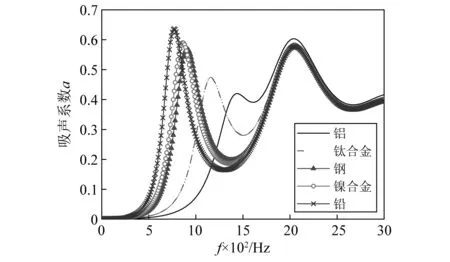
图8 芯体材料对吸声系数的影响Fig.8 The influence of core density on sound absorption coefficient

结果表明芯体材料对第一吸声峰的吸声系数幅值和位置影响很大，且随着材料密度增大，吸声峰频率降低，幅值增大。局域共振散射体模型的包覆层可类比为弹簧系统，大密度芯体类比为质量单元，根据弹簧-质量模型可知，随着质量增大，共振频率降低，振幅增大，因此铅对应的吸声系数峰值最大，出现波峰的频率最低。如图9(a)～图9(c)为散射体模型中面在铝、钢、铅芯体材料下第一吸声峰对应的位移云图，由图可知，各芯体材料对应的最大位移幅值分别为3.85×10-10m，6.14×10-10m和7.07×10-10m，即铅对应的最大位移幅值最大，表明铅芯体振动最剧烈，消耗能量最多，吸声系数最大。如图9(d)～图9(f)为散射体模型中面在各芯体材料下第二吸声峰对应的位移云图，位移几乎不发生变化，对应图8吸声系数几乎相等。

表4 芯体材料参数Tab.4 Material parameters of cores

图9 不同芯体材料下中面位移云图Fig.9 The mid-plane displacement fields at different core densities

2.3 包覆层厚度对吸声性能的影响

由Wen等和吕林梅等的研究可知包覆层对局域共振吸声结构吸声性能影响很大。以以上圆柱型局域共振散射体结构为研究对象，讨论包覆层厚度对吸声性能的影响规律。保持柱型局域共振结构的芯体结构不变，分别取包覆层厚度t为0.5 mm，1.0 mm，1.5 mm，2.0 mm和2.5 mm。包覆层厚度对结构吸声系数的影响如图10所示。由图及图形趋势可知，包覆层厚度为0.5 mm时，结构第一、第二吸声峰峰值和频率分别最高；随着厚度逐渐增大，局域共振吸声峰向低频移动；随着厚度增大吸声峰峰值减小且第一吸声峰减小幅度大于第二吸声峰。这是因为随着包覆层厚度增大，局域共振中包覆层刚度降低，局域共振散射体组成的弹簧质量模型等效刚度变小，导致吸声峰向低频移动。同时，随着包覆层厚度增大，局域共振中包覆层阻尼增加，由共振引起的吸声峰随着阻尼增加而降低。

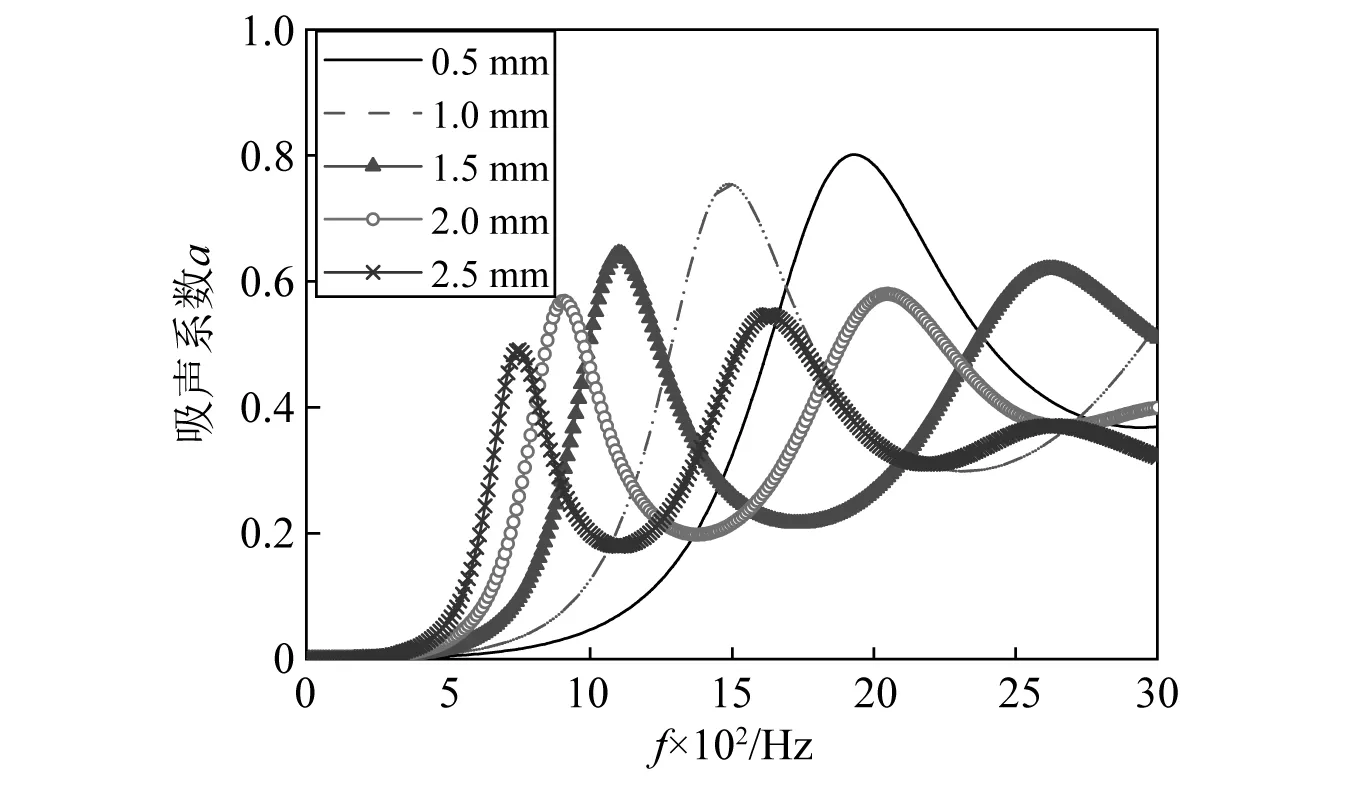
图10 包覆层厚度对吸声系数的影响Fig.10 The influence of coating thickness on sound absorption coefficient

3 变截面柱型局域共振散射体结构吸声性能优化设计

结合二维轴对称模型和遗传算法对变截面柱型局域共振型散射体结构的吸声性能进行优化设计。取整个吸声结构z方向的厚度范围为15～25 mm，令厚度H=(10hc+15)mm；整体模型半径范围为5～30 mm，令半径为Wr=(25W+5)mm，半径变化代表着晶格常数变化；取包覆层高度Hcoating=5 mm+b(H-7 mm)，高度方向保证基体厚度不小于1 mm；取芯材高度Hcore=3 mm+c(Hcoating-4 mm)，高度方向保证包覆层厚度不小于0.5 mm。设芯体截面半径和包覆层外径分别用N个控制点进行控制，各控制点在z方向等距Δh=Hcore/(N-1)，此处N取为5。包覆层外径为ricoating=3 mm+βi(Wr-4 mm)(i=1,2,3,4,5)，保证基体厚度不小于1 mm；芯体半径为ricore=1 mm+γi(ricoating-1.5 mm)(i=1,2,3,4,5)，保证包覆层厚度不小于0.5 mm。其中hc，W，b，c，βi，γi∈[0,1]，为几何因子。以上关系自然满足以下不等式，保证了优化过程的稳定性。

(3)

考虑基体厚度和半径、包覆层厚度和外径以及芯体半径对变截面柱型局域共振型散射体结构的平均吸声系数进行优化。优化参数向量为x=[hcWbcβ1β2β3β4β5γ1γ2γ3γ4γ5]，参数值变化范围均为[0,1]。遗传算法过程通过MATLAB遗传算法工具箱来实现。优化目标函数F为

F(x)=

(4)

式中，f为频率，频率范围[f1，f2]取为[1 kHz，3 kHz]，频率步长取为50 Hz。初始模型为图1(b)所示的圆柱型局域共振散射体结构，优化前后参数如表5所示。

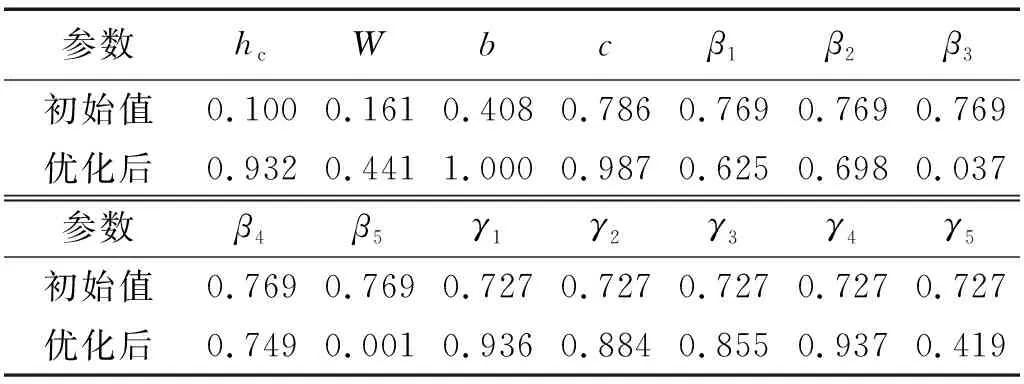
表5 优化参数Tab.5 Parameter value in optimization

图11为优化之后的变截面形状，图12为优化前后的吸声系数曲线图。由图可知优化后的吸声性能在全频段明显提高。

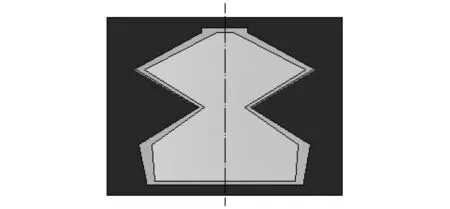
图11 优化后变截面形状示意图Fig.11 Schematic diagram of variable cross-section after optimization

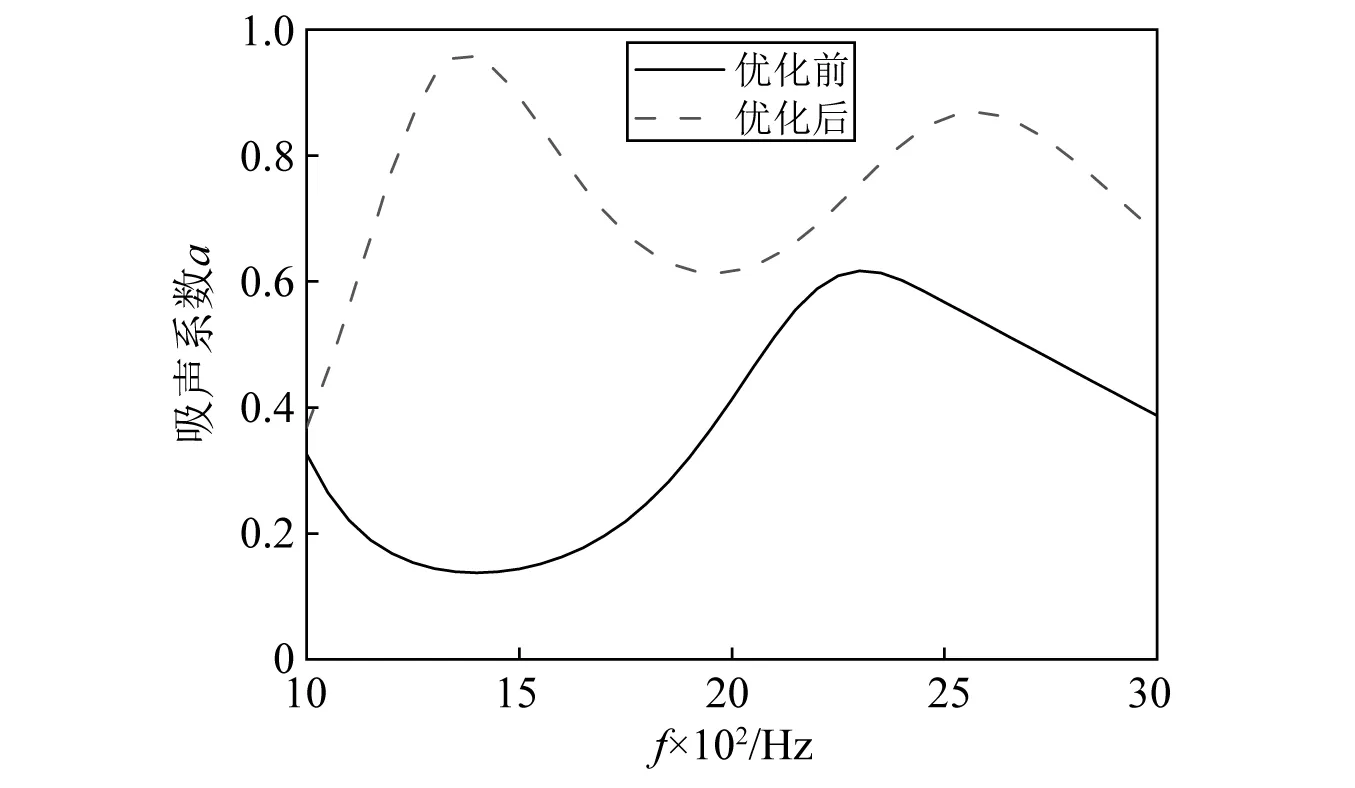
图12 优化前后吸声系数对比图Fig.12 Comparison of sound absorption coefficient before and after optimization

图13给出了优化后两吸声峰处对称面的位移分布云图和能量耗散密度分布云图。对比图13(a)与圆柱的第一吸声峰位移云图图6(b)可知，变截面芯体的平动带动包覆层变形的同时可以带动更多的基体变形，增加能量的耗散；对比图13(c)与图6(f)，包覆层能量耗散密度依然很大，但基体的能量耗散明显增加；对比图13(b)与图7(b)，变截面散射体的包覆层下部分发生旋转变形的同时，整个基体发生了较大变形，有利于能量在基体中的耗散；对比图13(d)与图7(f)，包覆层能量耗散密度依然很大，但基体中能量耗散密度明显增加。总的来说，变截面局域共振型散射体能激发更多基体变形从而耗散更多能量，可以为低频宽带吸声设计提供新的思路。因此工程实际中，在工艺条件允许的情况下，需要充分考虑到局域共振型结构的变截面参数优化。

图13 吸声峰处中面位移分布图和能量耗散密度分布图Fig.13 Mid-plane displacement and energy dissipation density distribution diagram at the sound absorption peaks

4 结 论

本文讨论了内嵌周期性局域共振散射体结构的吸声性能和吸声机理。该吸声结构的一个周期单元由软橡胶包覆大密度金属芯体内嵌于黏弹性材料基体中构成。对于轴对称局域共振散射体结构，本文建立并验证了二维轴对称模型的简化有限元方法。采用简化的有限元算法对局域共振散射体吸声结构讨论了截面形状、芯体材料以及包覆层厚度等参数对吸声性能的影响规律，结合吸声峰处位移云图和能量耗散密度云图分析了吸声性能的影响机理。最后对变截面柱型局域共振散射体吸声结构进行了优化设计。

通过讨论球型、圆柱型、圆锥台1和圆锥台2等散射体的吸声性能，可知各散射体结构第一吸声峰较窄，第二吸声峰更宽，散射体形状对第一吸声峰影响不大，对第二吸声峰影响较大。第一吸声峰由芯体的平动共振引起，芯体平动带动包覆层运动，促进波模式转换消耗声能，从而提高吸声系数。第二吸声峰主要由包覆层共振引起，能量集中耗散于散射体内。芯体和包覆层构成的散射体可以近似为质量弹簧模型，芯体密度增加引起模型质量增加，包覆层厚度增加引起模型刚度降低，但阻尼增加。因此随着芯体材料密度增加，第一吸声峰频率降低，峰值升高；随着包覆层厚度增加，吸声峰向低频移动，峰值降低。

采用遗传算法对变截面柱型局域共振散射体吸声结构在1～3 kHz频段内的平均吸声系数进行了优化，优化模型充分考虑了整个散射体厚度、晶格常数、芯体厚度、芯体截面半径、包覆层截面厚度等参数，优化后结构吸声系数在全频段内提高。机理分析表明各吸声峰处变截面散射体共振能激发更多的基体运动，增加波模式转换耗散声能。因此设计了变截面局域共振模型，该模型为低频宽带吸声提供了新的思路。