地质流体中络合物同位素平衡分馏系数的第一性原理计算*

孙明光，王佳新，袁顺达

(1中国地质科学院矿产资源研究所自然资源部成矿作用与资源评价重点实验室，北京 100037；2北京大学造山带与地壳演化教育部重点实验室，北京 100871)

流体的温度、压力、相态或络合物的价态及成键环境等的变化可以导致具有多种同位素的元素在迁移、富集和沉淀成矿过程中发生显著的同位素分馏，这些同位素分馏可以作为示踪流体地球化学过程的重要手段（Kelly et al.,1979;Sheppard.,1981;Gallagher et al.,1992;Rye,1993;Bethke et al.,2005;Dreher et al.,2008;Wen et al.,2015;Ohmoto,2018;Gao et al.,2018），尤其在示踪成矿物质来源、解释成矿元素同位素分馏机制及进一步确定矿床成因和建立成矿过程中相关同位素组成变化的模型等方面具有重要意义：如锡同位素分馏可以记录热液流体的氧化还原反应，从而可以用来解释含锡成矿流体的物理化学条件变化（Yao et al.,2018）；在热液体系中锑同位素分馏可以用来指示含锑成矿流体的流动方向，从而指示锑矿的勘查等（Zhai et al.,2021）。同位素质谱分析技术的革命性进展，尤其是多接收器等离子体质谱仪(MC-ICP-MS)的出现，推动了非传统稳定同位素尤其是金属稳定同位素地球化学的快速发展，并在地质研究中得到了广泛的应用。目前，锂、铁、镁、钙、钛、钒、镉等非传统稳定同位素在地表风化、表生环境、热液成矿等各类地质过程研究中发挥了越来越重要的作用，并取得了一系列重要进展（朱祥坤等，2013）。其中，对不同络合物之间的稳定同位素平衡分馏系数的测定是开展稳定同位素地球化学研究的必要前提。然而，一些元素由于易挥发、易氧化、相对质量差值小以及溶液中络合物难以分离测定等原因，导致实验方法无法测得溶液中一些元素不同络合物之间的平衡同位素分馏系数(Schauble,2004;Seo et al.,2007)，从而阻碍定量研究这些元素的同位素分馏机制。另外，在合理的时间尺度范围内，一些矿物-溶液之间的同位素交换平衡分馏系数难以通过实验手段获得，在一定程度上限制了这类同位素地球化学的推广应用（Schauble,2004）。

研究表明，基于密度泛函理论（DFT:density functional theory）的第一性原理计算是获得各类元素在不同络合物或矿物之间同位素分馏系数的一种重要手段（Cygan，2001）。目前，应用第一性原理计算溶液中络合物的约化配分函数比（β:reduced isotope partition function ratio）的模型主要有2种：显式溶剂模型（explicit solvation models）和隐式溶剂模型（implicit solvent model)。通过采用这2种模型，前人已经成功获得了一系列元素在不同物种之间稳定同位素的平衡分馏系数，如O、H、Cl、Fe、Mg、Si、Cu、Ag、Cd、Ge、Se、B、Br等（Seo et al.,2007;Méheut et al.,2007;2009;2010;Domagal-Goldman et al.,2008;Pinilla et al.,2015;Yang et al.,2015;Gao et al.,2018;Wang et al.,2019;Fujii et al.,2010;2013;2014;2018;Gao et al.,2021），在很大程度上推动了同位素地球化学的发展。然而，采用上述2种模型对溶液中的络合物进行模拟计算时，由于介质环境及络合物构型等方面存在明显不同，导致计算的结果往往会存在一定差异。本文对比研究了前人应用这2种模型对不同同位素体系的计算结果，进一步分析了这2种计算稳定同位素分馏系数方法的优、缺点，为今后开展第一性原理计算流体中络合物平衡同位素分馏时，为合理选择不同模型提供科学依据。

1 同位素分馏理论和计算方法

1.1 同位素分馏理论

同一元素不同同位素间质量差可以导致在各类地质过程中发生同位素分馏，因而在同位素交换反应达到平衡时，由于生成物和反应物的能量差别而发生同位素的平衡分馏。这种能量差极小，主要是由振动能引起的，因而可以依赖振动配分函数来计算2种络合物之间的同位素平衡分馏系数(Urey et al.,1933;Bigeleisen et al.,1947;Urey,1947)。2种物质A和B中的同位素交换反应：

A和A*分别代表的是含有同一元素的轻、重同位素的物质。平衡常数KA-B可以通过2种物质的约化配分函数比（β）的比值获得

反应式（1）中涉及到的是1个原子(n=1)的交换反应，因此分馏系数α可以替代K（α=K1/n），α=K。

β可以通过公式（3）获得：

其中

h和k分别是普朗克常数和玻尔兹曼常数，T是温度（Kelvin），υi表示原子的振动频率。通过公式（3）和公式（4），可得到只与振动频率υi有关的RPFR(β)。因此如果能够获得体系的振动频率，便可获得β及同位素平衡分馏系数。计算公式的详细推导及解释见Chacko等(2001)。

1.2 β值的计算方法

1.2.1 隐式溶剂模型

隐式溶剂模型是通过极化连续介质模型(PCM:Polarizable Continuum Models)的方法模拟溶液环境（Cances et al.,1997），该方法是将溶质置于一个被溶剂包围的反应场空腔中，且空腔外部的溶剂被定义为具有均匀介电常数的连续介质（widerek et al.,2019;Wilson et al.,2015;Li et al.,2009），图1为隐式溶剂模型，[Sn4+Cl4]（图1a）和[Sn2+Cl3]-（图1b）被置于空腔中，这种空腔简化了水溶液的动态特性，因而计算耗时降低。例如，Sun等（2022）应用

图1 优化后隐式溶剂模型的络合物分子结构a.[Sn4+Cl4];b.[Sn2+Cl3]-（据Sun et al.,2022）Fig.1 Complexes molecular structure of optimized implicit solvent model a.[Sn4+Cl4];b.[Sn2+Cl3]-（after Sun et al.,2022）

B3LYP(Becke-style 3-parameter density functional theory with the Lee-Yang-Parr correlation functional)(Lee et al.,1988;Becke,1993a;1993b)计算含锡络合物的分子结构和振动频率，使用混合基组对[Sn4+Cl4]和[Sn2+Cl3]-进行结构优化和频率计算,其中对Cl原子使用6-311+G(d,p)基组，Sn原子使用SDD(Stuttgart-Dresden relativistic effective core potential)(Schwerdtfeger et al.,1989），上述计算均基于Gaussian 16软件（Frisch et al.,2016）。通过Gaussian View可视化软件，分别搭建[Sn4+Cl4]和[Sn2+Cl3]-络合物合理的分子结构，然后依次选择上述的计算基组提交计算任务（依次计算124Sn、116Sn），计算完成后从输出文件中检查振动频率是否有虚频，若无虚频则可通过公式（3），求得β值；若有虚频表明此时的分子结构不稳定，体系能量不是最低，因而需要进一步调整分子结构重新提交计算任务，直至无虚频为止。

1.2.2 显式溶剂模型

为精确处理溶液中水分子的相互作用、水的动态特征和氢键对β值的影响，前人通过在溶质周围添加水分子的方法对溶液环境进行模拟，故称为显式溶剂模型，此方法能够很好地描述水溶液的动态特征（Liu et al.,2005;Li et al.,2009;2011;Wu et al.,2015;Gao et al.,2018;Wang et al.,2019;Gao et al.,2021）。图2a、b为基于显式溶剂模型对[Sn4+Cl4]和[Sn2+Cl3]-的结构优化图，图中可以显示[Sn4+Cl4]和[Sn2+Cl3]-被周围的水分子包裹。Sun等（2022）应用第一性原理分子动力学方法（first-principles molecular dynamics(FPMD)）对[Sn4+Cl4]和[Sn2+Cl3]-络合物进行模拟计算。首先，对2个含锡络合物在溶液中的动态特征进行模拟，计算采用NVT热动力学系综（NVT thermodynamic ensemble）(即在模拟计算过程中原子数(n),体积(V)和温度(T)固定不变，压力(P)和 能量(E)允许改变)。面波能量截取设置为600 eV，布里渊区k点 为1×1×1。已有研究表明，在模拟计算过程中50个水分子就能够真实反映溶质所处的溶液环境，且获得精确的β值(Wang et al.,2019;Gao et al.,2021)，因而笔者的计算也在[Sn4+Cl4]和[Sn2+Cl3]-溶质周围添加了50个水分子。为保持整体电荷平衡，在[Sn2+Cl3]-溶液中添加了1个Na离子。参数设置确保了静态压力接近0，密度设置为水的密度1 g/cm3。模拟2个络合物在溶液中的动力学特征的时间步长为1 fs，模拟的总时间是50 ps（50 000 fs），以获得足够的构型去计算每个络合物的β值。应用VASP软件能够较简便的建立团簇模型，可以通过设置时间步长(1 fs)和模拟计算的总时间（ps）来获得不同的构型，比Gaussian软件的处理过程相对简单，但计算耗时较长，比如，通过改变[Sn4+Cl4]和[Sn2+Cl3]-络合物的输入文件，分别获得[Sn4+Cl4]和[Sn2+Cl3]-的50 000个构型，体系的温度和能量变化（图3a～d）趋势表明，在30 ps至50 ps之间体系能量变得稳定，因此在30 000至50 000构型之间每隔2 ps(2000构型)取1个构型，对获得的10个不同构型结构优化，使用优化后的构型进行频率计算，最终通过公式(3)得出每个络合物的β平均值。

图2 优化后显式溶剂模型的络合物分子结构a.[Sn4+Cl4](H2O)50(扩胞：2×2×2);b.[Sn2+Cl3]-(H2O)50(扩胞：2×2×2)绿色表示Cl原子；红色表示O原子；白色表示H原子；紫色表示Sn原子；黄色表示Na原子；虚线为分子动力学模拟完成后H2O分子之间形成的氢键（据Sun et al.,2022）Fig.2 Complexes molecular structure of the optimized explicit solvent model a.[Sn4+Cl4](H2O)50(super cell：2×2×2);b.[Sn2+Cl3]-(H2O)50(super cell：2×2×2)Colorsfor atoms:chlorine,green;hydrogen,white;tin,purple;sodium,yellow;thedotted lineshowsthehydrogen bond formed between H2O molecules after molecular dynamics simulation(after Sun et al.,2022)

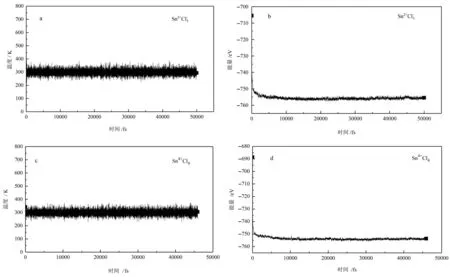
图3 [Sn4+Cl4]和[Sn2+Cl3]-分子动力学(FPMD)模拟过程中温度和能量随时间的变化趋势Fig.3 Variation trend of temperature and energy with time of[Sn4+Cl4]and[Sn2+Cl3]-complexes during molecular dynamics(FPMD)simulation

2 隐式溶剂模型与显式溶剂模型对比

为了对比2种模型对络合物平衡同位素分馏系数计算结果差异，本研究系统收集了前人通过隐式或显式溶剂模型计算的B、Se和Sn同位素计算结果（表1）。从0～350℃，以隐式溶剂模型计算的[Sn2+Cl3]-的β值范围为1.002 084～1.000 406，[Sn4+Cl4]的β值范围为1.005 445～1.001 082，以显式溶剂模型计算的[Sn2+Cl3]-和[Sn4+Cl4]的β值范围分别为1.002 385～1.000 473和1.006 877～1.001 394（Sun et al.,2022），且在对Sn2+Cl3-络合物执行分子动力学过程中，有1个水分子与Sn结合，此时的Sn2+Cl3-络合物的配位数为4，配位元素为Cl和O，而隐式溶剂模型对此无法模拟。根据计算结果表明，在恒定温度条件下同一种模型计算的β值的变化趋势为[Sn4+Cl4]＞[Sn2+Cl3]-，这与前人得出高价态同位素富集重同位素的结论相一致(She et al.,2020;Wang et al.,2021),且随着温度的增加[Sn4+Cl4]和[Sn2+Cl3]-的β值都逐渐降低（图4a、b）。虽然这种变化趋势是一样的，但是2种模型计算的β值有明显的差异，如在25℃条件下，[Sn2+Cl3]-在隐式和显式溶剂模型下的β值分别为1.001 755和1.002 014，[Sn4+Cl4]的β值分别为1.0046和1.005 829(表1)。此外，前人采用隐式溶解模型和显式溶剂模型对同一络合物β值的计算结果也存在一定差异：如在25℃，对流体中B（硼）络合物B(OH)3，以隐式溶剂计算的β值为1.2313，以显式溶剂模型（B(OH)3-(H2O)34）计算的β值为1.2267（表1）（Liu et al.,2005）；同样，在25℃时，流体中Se络合物以隐式溶剂模型计算的β值为1.0350，而显式溶剂模型计算的β值则为1.0243（Li et al.,2011）。下面从以下3个方面对比研究这2种模型的主要差异。

图4 两种模型计算的Sn2+Cl3-和Sn4+Cl4络合物的1000lnβ值（a）和1000lnα值（b）Fig.4 1000lnβ(a)and 1000lnα(b)values of Sn2+Cl3-and Sn4+Cl4 complexes calculated by two models

表1 2种模型计算的不同元素的β值(0～350℃)Table 1 βvalues for different elements calculated by the two models(0～350℃)

2.1 两种模型计算β值耗时对比

隐式溶剂模型计算络合物的β值并不增加溶质周围的原子数目（图1a、b）。已有研究表明，通常情况下，无机络合物的单体溶质原子的数目一般较少（1～20），如HSe-（2）、Fe(H2O)62+（19）、Fe(H2O)63+（19）、Ge(OH)4（9）和V4+O(H2O)52+（17）等（Jarzecki et al.,2004;Li et al.,2009;2011;Wu et al.,2015），对隐式溶剂模型下的络合物分子结构优化和频率计算的过程中，若每个络合物分子分配32个核数进行计算，大约耗时数个小时即可计算完成，且计算完成后输出的结果文件大小仅为数兆（M）。而显式溶剂模型需要在络合物周围添加不同数量的水分子,计算的原子数目增加，如B(表1)，Sn(图2)，Ge和Se（表2），每个络合物计算的原子数目范围为20～154（表2）。而且由于络合物构型对β值有影响，使得每个络合物必须计算不同的构型（2～10个），因而在使用与隐式模型计算相同的基组水平对显式溶剂模型下的络合物进行计算时（Gaussian软件），耗时比隐式溶剂模型所需更久，根据络合物数量可能需要数月，计算完成后输出的结果文件为数十兆至数百兆，如VASP计算的Sn2+Cl3--(H2O)50和Sn4+Cl4-(H2O)50的结果文件可以达到2 G～3 G。

2.2 两种模型计算时水分子数和构型对β值的影响

隐式溶剂模型的方法计算的络合物只有一种构型，因而不能评估不同构型(configurations)对络合物β值的影响，如前人对B、Se和Sn络合物β值的计算即只有一个构型（表1）。相对而言，采用显式溶剂模型的方法对络合物β值计算时，可以建立多种初始构型（如表2中A、B、C、D为4种不同的构型），且不同构型其β值也有一定差异（表2），表明构型是影响β值的因素之一，因而在计算流体中络合物的平衡分馏系数需考虑构型的影响。如前人计算B、Se、Sn和Ge络合物的β值，分别通过建立多种构型来计算β值，并最终采用不同构型获得β值的平均值作为络合物的β值，从而降低构型对计算结果的影响（表2）（Liu et al.,2005;Li et al.,2009;2011;Wu et al.,2015）。

表2 不同水分子数和不同构型的Ge、Se和B络合物的β值（A、B、C和D表示不同的构型）Table 2 βvalues of Ge,Se and B complexes with different numbersof water molecules and different configurations(A,B,C and D represent different configurations)

隐式溶剂模型对溶质周围水环境的模拟方法较为简单，因而该方法不能系统评估水分子数的变化对计算结果的影响。显式溶剂模型则可通过在溶质周围添加一系列的水分子建立不同的团簇模型的方法（如6、12、18、24和30）来评估水分子数量差异对β值的影响（表2）：例如，Liu等(2005)从计算B(硼)最小的构型开始，逐渐增加溶质周围的水分子数量（6、12、8、24和30），计算的结果表明，随着水分子数的增加，各构型之间的β值差异逐渐降低，如30个水分子模型B(OH)3-(H2O)30_C和34个水分子模型B(OH)3-(H2O)34之间的β值相差为0.0004（表2），这种差异对于目前自然体系B同位素分馏水平可忽略不计，因此，30或34个水分子足以获得B络合物稳定的β值，无需进一步计算更多水分子的硼络合物的β值。同样，Li等（2009）建立了一系列的模型研究Ge络合物的β值，在每次优化“水滴团簇模型”时确保了最小的模型（6个H2O分子）的能量为最低，结构最稳定，在上一个模型的基础上增加6个水分子直至30，随着水分子数的增加，计算获得的β值变化逐渐减小。Li等(2011)计算Se络合物之间的β值，也通过建立了一系列的模型（6、12、18和24）计算Se络合物的平均β值（表2）。基于同样的方法，前人也成功预测了V（钒）络合物的平衡同位素分馏系数（Wu et al.,2015）。因此，在计算流体中络合物同位素分馏时络合物的构型和水分子数量对其β值的计算产生一定影响，相比于隐式溶剂模型，显式溶解模型在计算络合物β值时更能充分的评估络合物构型及水分子数对计算结果的影响。

2.3 两种模型模拟的水溶液环境对β值的影响

根据前人应用隐式溶剂模型和显式溶剂模型对B，Se和Sn络合物的β值计算结果表明，不同模型计算络合物的β值有明显的差异（表1、表2），如B(OH)3络合物的β值分别为1.2313（B(OH)3）和1.2267（B(OH)3-(H2O)34），SnCl3-的β值分别为1.001 755（SnCl3-）和1.002 014（SnCl3--(H2O)50），SnCl4的β值分别为1.0046（SnCl4）和1.005 829（SnCl4-(H2O)50），的β值分别为和1.038 29造成这种差异的原因是两种模型对水环境的模拟方式不同。

隐式溶剂模型虽然可通过应用PCM方法对溶质周围的水环境进行模拟，但该模型把溶质周围的水定义成具有均匀介电常数的连续介质，处理水的动态特性及水分子之间形成的氢键精确度稍低（Liu et al.,2005;Li et al.,2011;2009）。尽管可通过Gaussian软件中的多种PCM(UAHF,UA0,CPCM和SCIPCM)模型，可以提高计算过程中对溶液水环境中氢键模拟的精确度，已有学者通过PCM UA0模型计算获的B(OH)3的振动频率值（885 cm-1）与实验测定值(880 cm-1)具有较好的一致性（Liu et al.,2005），但计算的β值与实验测定值仍存在明显差异（Klochko et al.,2006;Byrne et al.,2006;Rustad et al.,2007）。为了更好的模拟溶液的动态特征，并合理表达溶质与周围水分子之间的相互作用，Liu等(2005)采用显式溶剂模型（水滴团簇模型：water-droplet），在硼络合物周围添加了不同数量的H2O分子来模拟溶质周围的水环境（表1）。虽然这种模型对计算的要求高，但是只要团簇模型足够大，计算的结果精度就越高（Liu et al.,2005）。基于该显式溶剂模型，能够使溶质周围形成至少2～3层水分子，且每个水分子在自身的位置形成两个或更多的氢键，最终形成由4、5和6个水分子组成的多个环状团簇，从而在溶质周围的水分子之间形成了更真实的氢键环境。图2展示出在计算完成后，水分子由于相互作用形成的氢键（图中虚线所示）及团簇。基于显式溶剂模型，Liu等(2005)成功预测了B(OH)3和B(OH)4-之间的同位素分馏系数，并且被后续的实验和计算结果所证实(Klochko et al.,2006;Byrne et al.,2006;Rustad et al.,2007)。

除此之外，Li等(2009)通过PCM方法和显式溶剂模型方法计算同一Ge络合物的1000lnβ值，计算结果表明虽然2种模型计算出的Ge-O键长几乎一致，但是1000lnβ值仍有明显的差异，尤其是对部分高负价态的络合物，差异更加明显，而且隐式溶剂模型（PCM方法）计算时假设络合物中Ge-O键长相等的结构是高度对称的，即使在输入文件中写入关键词“nosymm”(not assume any symmertry),但是从输出的结果可以看出分子结构仍然是对称的。然而，分子结构的高度对称是不真实的，因为溶质和水分子外层形成的氢键在不同的方向结构不可能是相同的。因此，虽然隐式溶剂模型对络合物分子结构的优化能够得到与显式溶剂模型一致的键长，但是由于隐式溶剂模型对水环境的模拟没有显式溶剂模型精确，仍然导致2种模型计算的结果不一致(Li et al.,2009)。

综上所述，应用隐式溶剂模型计算溶液中络合物的β值有一定的局限性，虽然计算量相对小，能明显节省计算时间，但是不能精确处理溶液中水分子之间的相互作用、强氢键，也不能有效评估构型对β的影响。而显式溶剂模型通过在溶质周围添加水分子的方法，可以更好的模拟真实溶液环境，而且随着水分子数量的增加，计算的结果越精确，随着水分子数增加，能够逐渐真实反映溶质所处的溶液环境，并获得精确的β值（Wang et al.,2019;Gao et al.,2021）。由于溶液的动态特征导致络合物存在各种构型，为了降低构型对计算结果的影响，前人在保持溶质周围水分子数量相同的条件下，对每个络合物建立不同的构型，最终计算获得β值的平均值。因此应用显式溶剂模型计算水溶液中络合物的同位素分馏系数时需要考虑溶质周围添加的H2O分子数量和不同构型对计算结果的影响，从而尽可能降低计算误差。如图4a所示，虽然显式溶剂模型和隐式溶剂模型计算的Sn4+Cl4络合物的1000lnβ值相差不大，但是Sn2+Cl3-的1000lnβ有较大的差异，而且Sn4+Cl4和Sn2+Cl3-之间的平衡锡同位素分馏系数1000lnα（图4b）也有较大差异，这主要是由于隐式模型忽略了水的构型和水分子与溶质之间相互作用对β值的影响，而显式模型则充分模拟了构型和水分子之间的相互作用。

3 结论

显式溶剂模型和隐式溶剂模型是计算溶液中各络合物之间的平衡同位素分馏系数的2种主要模型，但是由于这2种模型对溶液模拟的方式不同，导致计算耗时及β值有差异，具体表现为：①隐式溶剂模型计算的原子数量较少、计算的速度快、耗时少。显式溶剂模型涉及的水分子数量和构型多，因此需要计算的原子数量多且需要反复计算不同的构型，导致耗时久；②溶质周围水分子数和构型对β值的影响：隐式溶剂模型对水溶液环境模拟的较为简单，导致络合物只有一个构型；显式溶剂模型通过建立一系列的水分子数和构型评估它们对计算结果的影响，最终通过求各构型的平均值降低这些因素引起的误差；③隐式溶剂模型把溶质周围的水定义成具有均匀介电常数的连续介质，这不能很好的处理水的动态特性及水分子之间形成的氢键，导致计算的结果与实验值偏差较大；显式溶剂模型能更好的模拟溶液的动态特征，且表达溶质与周围水分子之间的相互作用，能获得更加精确的β值。因此，目前已有研究表明：显式溶剂模型是计算溶液中络合物之间平衡同位素分馏的更为有效的手段。

致谢感谢审稿人百忙之中抽出时间审阅本文，为本文提出的建设性意见，从而使得文章语言表达通畅，逻辑更加清楚，文章有了质的提升。